1. 디랙 델타 함수
2. 맥스웰 방정식
3. 페이저를 이용한 맥스웰 방정식
5. 적분 방정식의 의미
[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11a)
(11b)
여기서 $\bar M(\bar r')$은 자류 밀도(magnetic current density), $G_F(\cdot)$는 전기 벡터 포텐셜용 그린 함수이다. 전기 벡터 포텐셜이 자류 밀도와 그린 함수로 정의되므로, $\bar F(\bar r)$로 생성되는 전자기장을 매우 쉽게 표현할 수 있다.
[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.
조금 공부해보면 알지만 미분 방정식(differential equation)은 우리가 알고 있는 단순한 방정식중 하나가 아니다. 방정식의 해답을 구하기가 매우 어렵고 답을 구하는 절차도 그때 그때 다르기 때문에 미분 방정식은 풀이법 자체가 매우 어렵다. 그래서 방정식이란 이름이 들어갔다해서 미분 방정식을 1차 연립 방정식(simultaneous linear equation) 수준으로 생각하면 곤란하다. 물론 미분 방정식보다 더 어려운 방정식은 적분 방정식(integral equation)이다. 미분 방정식이 미지수를 미분한 형태로 표현되었다면 적분 방정식은 미지수를 정적분(definite integral)한 형태로 표현된다. 정적분으로 표현되기 때문에 식을 미분해서 적분 방정식을 미분 방정식으로 변환할 수는 없다. 왜냐하면 부정적분(indefinite integral)이 아닌 정적분이기 때문에 적분 기호 바깥에서 미분하더라도 적분이 없어지지 않는다. 이를 이해하려면 식 (10)을 한 번 미분해보라. 적분이 없어지는가? 없어지지 않는다.
적분 방정식보다는 수월하지만 여전히 복잡한 형태를 가진 미분 방정식을 해석적으로 푸는 표준적인 방법론은 푸리에 급수(Fourier series)와 푸리에 변환(Fourier transform) 혹은 그린 함수(Green's function)가 될 수 있다.[어떤 특정한 적분 방정식도 푸리에 변환을 통해 풀어낼 수 있다.] 그린 함수의 그린은 색깔이 아니다. 전설적인 영국의 수학자 그린George Green(1793–1841)이다. 그린이란 수학자는 수학사를 연구하는 사람들에게는 이해 못할 특이한 사람이다. 그린의 원래 직업은 빵을 만드는 제빵사(baker)와 밀을 빻는 방앗간 주인(miller)이었다. 그런 제빵사가 그린 정리(Green's theorem), 그린 함수 개념을 만들었다. 그린이 받은 정규 교육은 1년 정도가 전부였다. 주변에 도서관도 없어서 이웃 도시 도서관만 간간이 이용했어야 할 정도로 주변 교육 시설도 열악했다. 그런데 불현듯 35세[1828년]에 그린 정리와 그린 함수 이론을 발표했다[2]. 대부분은 학교에서 열심히 공부한 후에 더 연구를 해서 논문을 쓰지만, 그린은 빵을 만들다가 틈틈이 쉬는 시간에 수학을 연구해서 새로운 수학 정리를 발견했다. 뒤늦게 자신의 수학적 재능을 발견해서 매우 늦은 나이인 39세[1832년]에 케임브리지 대학교(University of Cambridge)에 입학해 새내기가 되었다. 우리와 비교해보면 이런 의외의 부분이 19세기 영국의 경쟁력이었다. 19세기 영국에서는 초등학교도 못나온 제빵사가 수학자가 되고[그린을 말한다.], 초등학교도 못나온 제본기사가 실험 과학자가 되고[패러데이(Michael Faraday)를 말한다.], 지방 출신에 지방대 나온 촌뜨기가 20대에 물리학 교수가 되고[맥스웰(James Clerk Maxwell)을 말한다.], 성격 나쁘고 귀가 불편한 장애인이 이론 물리 연구자로 성공하고[헤비사이드(Oliver Heaviside)를 말한다.], 섬마을 술주정뱅이가 천문대장[해밀턴(Sir William Rowan Hamilton)을 말한다.]을 했다. 19세기 영국과 비교해 대한민국은 얼마나 열린 사회인지 수학자 그린을 통해 다시 한 번 생각하게 된다.
그린 함수의 중요 지배 방정식을 유도하자. 먼저 페이저(phasor)를 이용하면 맥스웰 방정식(Maxwell's equations)이 아래의 헬름홀츠 방정식(Helmholtz equation)이 된다.
(1) (2)
여기서 $k$는 파수(波數, wavenumber)이다. 그린 함수를 써서 어떤 물리 구조에 대한 식 (1)의 스칼라 포텐셜(scalar potential) 해를 구해보자. 먼저 디랙 델타 함수(Dirac delta function)를 이용해 전하 밀도(electric charge density)를 적분으로 바꾸어보자.
(3)
식 (3)에 출현한 3차원 델타 함수는 아래로 정의한다.
(4)
식 (3)을 이용하면 그린 함수를 정의하는 지배 방정식을 다음처럼 얻을 수 있다.
(5)
식 (5)를 잘 보면 그린 함수는 선형 시스템(linear system)의 임펄스 응답(impulse response)이다. 그러면 식 (1)의 해를 그린 함수 관점에서 아래처럼 쓸 수 있다.
(6)
물론 식 (1)은 미분 방정식이므로 식 (6)은 전하 밀도가 존재하는 경우의 특수해(particular solution)가 된다. 식 (2)의 자기 벡터 포텐셜(magnetic vector potential)도 동일한 방법으로 구할 수 있다.
(7)
식 (7)과 (5)를 고려하면 자기 벡터 포텐셜은 아래로 표현된다.
(8)
여기서 $G_A(\cdot)$는 자기 벡터 포텐셜에 대한 그린 함수이다.[그린 함수는 식 (5)와 경계 조건(boundary condition)을 이용해 결정하므로 스칼라 포텐셜과 벡터 포텐셜의 그린 함수는 다를 수 있다.] 만약 그린 함수만 알 수 있다면 그린 함수 개념을 이용하면 식 (6)이나 (8)처럼 모든 선형 미분 방정식(linear differential equation)을 풀 수가 있다. 하지만 그린 함수 구하기는 몇몇 예외를 제외하고는 쉽지 않다. 또 하나 전하 밀도 $\rho$나 전류 밀도(electric current density) $\bar J$를 모르기 때문에 문제 풀이가 매우 어려워진다. 사실 전자파 문제를 푼다는 뜻은 $\rho, \bar J$ 구하기를 의미한다. $\rho, \bar J$를 이용해 전기장(electric field)과 자기장(magnetic field)을 구하면 정방향 문제(forward problem)라 한다. 전기장과 자기장의 경계 조건을 이용해 $\rho, \bar J$를 정하면 역방향 문제(inverse problem)라 부른다. 역방향 문제는 대표적인 적분 방정식 문제이다. 적분 방정식의 의미를 이해하기 위해 식 (8)을 이용해 자기장과 전기장을 구해보자.
(9)여기서 $\bar \nabla$가 포함하는 편미분은 관측점 $\bar r$ = $(x, y, z)$이 기준이고 체적 적분은 $\bar r$에 독립적인 원천점 $\bar r'$ = $(x', y', z')$에 대해 수행하므로, 편미분과 적분은 상호 교환이 가능하다. 예를 들어, 물리 구조가 완전 전기 도체(完全電氣導體, Perfect Electric Conductor, PEC)라면 전기장의 접선 성분(tangential component)이 0이 된다. 그러면 전류 밀도 $\bar J$는 다음을 만족하도록 결정되어야 한다.
(10)
식 (10)에서 그린 함수 $G_A$는 결정되어 있으므로 미지 함수인 $\bar J$를 조정해서 식 (10)을 만족시켜야 한다. 그런데, 이 과정이 쉽지 않다.[∵ 식 (10)을 한 번 풀어보라. 완벽하게 풀 방법이 있는가?] 수학적으로 완벽한 기법을 써서 식 (10)의 적분 방정식(integral equation)을 풀 수 있는 방법은 아직 없다. 그래서 푸리에 급수(Fourier series)를 흉내낸 근사를 한다. 즉, 전류 밀도(electric current density) $\bar J$를 적절한 기저 함수(basis function)로 표현해서 식 (10)을 적분 방정식이 아닌 연립 방정식(聯立方程式, simultaneous equations)으로 만들어 전자파 문제를 근사적으로 푼다. 이런 접근법은 MoM(모멘트 기법, Method of Moments)이라 부른다. MoM을 최초한 제안한 사람은 러시아 기계 공학자 겸 응용 수학자인 갈레르킨Boris Grigorievich Galerkin(1871–1945)이다[1]. 갈레르킨이 1915년경갈레르킨 44세, 일제 식민지 시절에 MoM을 제안했지만 당시에는 컴퓨터가 없어 한동안 잊혀져 있다가 1960년경해링턴 35세, 장면 정부 시절에 해링턴Roger F. Harrington(1925–)에 의해 MoM이 재발견되었다[1]. 모멘트 혹은 능률(能率, moment)은 두 물리량의 곱 형태로 공식화한 핵심 측정량(measure)을 의미한다. 물리학에서는 보통 수직한 길이를 기준으로 모멘트를 만들지만 필수는 아니다. MoM에서 말하는 모멘트는 길이가 아니고 전류 분포이니 말이다. 혹은 물리학 개념을 빌려서 통계학에서 사용하는 적률(積率, moment)도 모멘트의 어원이다. MoM 제안자인 해링턴은 MoM에 출현하는 적분의 이름을 붙이기 위해 통계학의 적률 개념을 빌렸다[1]. 통계학에서 함수 $f(x)$의 $n$차 적률은 $\int x^n f(x)\,dx$이다. 적분이 들어간 적률 정의에서 $x^n$ 대신 가중치 함수 $w_n (x)$로 바꾸면, MoM에서 사용하는 모멘트 정의인 $\int w_n (x) f(x)\,dx$가 된다.
식 (8)과 동일한 방식을 도입해서 그린 함수를 사용한 전기 벡터 포텐셜 $\bar F(\bar r)$을 깔끔하게 공식화한다.[편하게 이해하려면 맥스웰 방정식의 쌍대성(duality of Maxwell's equations)을 쓴다.]
(11a) (11b)스튀름–리우빌 이론(Sturm–Liouville theory)을 이용해서 그린 함수를 고유치(eigenvalue)와 고유 함수(eigenfunction)로 표현한다. 먼저 식 (5)를 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation) 형태로 쓰면 다음과 같다.
(12)여기서 $\lambda$는 미분 방정식의 고유치이다. 스튀름–리우빌 이론에 따라 식 (11)에서 얻어지는 제$m$번 고유치 $\lambda_m$과 고유 함수 $\psi_m(x)$의 관계는 다음처럼 쓰여진다.
(13)
(14)또한 고유 함수의 완비성(completeness of eigenfunctions)에 의해 그린 함수 $g(x, x'; \lambda)$는 기저가 $\psi_m(x)$인 무한 급수로 전개된다.
(15)여기서 $g_m(x'; \lambda)$는 $\psi_m(x)$의 계수이다. 식 (14)와 (15)를 식 (12)에 대입해서 $\psi_m(x)$에 대해 정리한다.
(16)식 (16)에 고유 함수의 직교성(orthogonality of eigenfunctions)을 적용해서 $g_m(x'; \lambda)$를 엄밀하게 결정한다. 따라서 그린 함수는 고유치와 고유 함수로 정확하게 표현된다.
(17)식 (17)에서 $\lambda$ = $\lambda_m$을 포함하도록 복소 적분의 닫힌 경로 $c$를 정의한 후 코쉬의 적분 정리(Cauchy's integral theorem)를 적용한다.
(18)여기서 $\psi_m(x)$는 $\lambda$에 대해 극점(pole)이나 가지 자름(branch cut)이 없다. 결과적으로 그린 함수와 디랙 델타 함수는 코쉬의 적분 정리에 의해 서로 밀접하게 연결되어 있다.
[그림 1] 무한한 정의역을 위한 적분 경로
그린 함수가 정의된 정의역이 유한한 식 (17)과는 다르게 정의역이 무한대로 확장되는 경우는 고유치가 이산적이 아니고 연속이 된다. 왜냐하면 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)의 정의역 비율 조정(domain scaling)에 대한 성질으로 인해 정의역 구간이 확대될수록 두 고유치의 차이가 줄어들기 때문이다. 이로 인해 정의역 구간이 무한이면, 두 고유치의 차이는 0으로 수렴해서 연속적인 고유치가 된다. 즉, [그림 1]에 표시한 가지 자름(branch cut)은 이산적인 고유치가 연속하면서 자연적으로 형성된다. 그래서 식 (18)은 무한한 정의역 혹은 연속적인 고유치 조건에서 다음처럼 변형된다.
(19)식 (18)과 다르게 식 (19)에 나타난 복소 적분은 닫힌 경로가 아닌 열린 경로에서 정의된다. 이산적인 고유치 조건에서는 고유치 사이로 적분 경로가 통과할 수 있어서 식 (18)처럼 닫힌 경로가 된다. 반면에서 [그림 1]처럼 고유치가 연속이면, 경로를 어떻게 변형하더라도 연속적인 고유치를 통과할 수 없다.[$\because$ 고유치에서는 해석적이 아니기 때문이다.] 이 경우는 식 (19)처럼 디랙 델타 함수를 만드는 적분은 반드시 열린 경로에서 정의되어야 한다. [그림 1]처럼 가지 자름을 피하는 경로인 $c_1+c_2+c_3+c_R$에 대해 코쉬의 적분 정리(Cauchy's integral theorem)를 적용하면 다음 관계도 유도할 수 있다.
(20)식 (26)처럼 그린 함수를 미소 구간[$x'-\Delta \le x \le x'+\Delta$]에 대해 적분해보면, 그린 함수는 모든 점에서 항상 연속이고 그린 함수의 미분은 도약 조건(jump condition)을 가져야 한다. 더 구체적으로 식 (12)의 좌변을 미소 구간에 대해 적분한 경우, 점 $x$ = $x'$ 근방에서 그린 함수가 가져야 하는 연속 및 도약 조건은 다음과 같다.
(21)
(22)여기서 $A$는 상수, $g_l(x; \lambda)$와 $g_u(x; \lambda)$는 각각 $x \le x'$와 $x \ge x'$ 구간에서 그린 함수의 변화 특성을 규정한다. 최소수 $x_<$와 최대수 $x_>$의 개념을 이용해서 식 (22)를 더 간결하게 표기하기도 한다.
(23)여기서 $x_<$ = $\min(x, x')$, $x_>$ = $\max(x, x')$이다. 식 (21) 혹은 (22)에 도약 조건을 적용해서 $A$를 결정한다.
(24)여기서 $g'(x; \lambda)$ = $dg(x; \lambda)/dx$, $W(u, v)$는 함수 행렬식(Wronskian)이다. 식 (24)를 식 (23)에 대입해서 간략화된 그린 함수의 표현식을 얻는다.
(25)식 (5)에 의해 결정되는 그린 함수가 가진 성질은 다음과 같다.
- 연속성(continuity)
식 (17)에 의해 $\bar r \ne \bar r'$인 점에서 그린 함수가 연속임은 명백하다. 점 $\bar r$ = $\bar r'$ 근방의 연속성을 구하기 위해, 식 (5)를 매우 작은 체적 $v$에 대해 적분하고 발산 정리(divergence theorem)를 적용해서 정리한다.
(26)미소 체적 $v$가 $0$으로 갈 때, 그린 함수가 $\bar r$ = $\bar r'$에서 불연속이면 그린 함수의 구배(gradient)는 발산한다. 이 경우에 구배의 면적 적분도 발산하므로, 식 (26)은 성립할 수 없다. 따라서 그린 함수는 모든 점에서 연속이 되어야 한다. 또한 그린 함수가 연속이라서 미소 체적 적분의 기여는 $0$이기 때문에, 식 (26)에 나온 구배의 면적 적분은 식 (21)에 있는 도약 조건을 꼭 포함해야 한다.
- 대칭성(symmetry)
원천에 해당하는 디랙 델타 함수는 $\delta(\bar r - \bar r')$ = $\delta(\bar r' - \bar r)$이 성립하기 때문에 $g(\bar r, \bar r'; k)$ = $g(\bar r', \bar r; k)$을 만족한다.
- 병진 불변성(translation invariance)
디랙 델타 함수의 입력 변수가 $\bar r - \bar r'$이므로, 원천에 대한 응답인 $g(\bar r, \bar r'; k)$도 병진에 대해서 불변성을 가진다. 따라서 그린 함수를 간단하게 $g(\bar r - \bar r'; k)$로 공식화할 수 있다.
[참고문헌]
[1] R. F. Harrington, "Origin and development of the method of moments for field computation," IEEE Antennas Propagat. Magazine, vol. 32, no. 3, pp. 31–35, June 1990.
[2] I. Grattan-Guinness, "Why did George Green write his essay of 1828 on electricity and magnetism?," The American Mathematical Monthly, vol. 102, no. 5, pp. 387–396, 1995.
[다음 읽을거리]
1. 1차원 자유 공간 그린 함수
2. 2차원 자유 공간 그린 함수
3. 3차원 자유 공간 그린 함수
4. 프란츠 공식
5. 다이애드 그린 함수
(1)
(1)
(2a)
(2b)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11).svg/500px-Sinc_function_(both).svg.png)
(12)
(13)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(26)
(27)
(34)
(35)
(36)
(37)
(41)
(44)
(47)
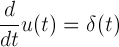(1.8)