디랙 델타 함수(Dirac Delta Function)

[경고] 아래 글을 읽지 않고 "디랙 델타 함수"를 보면 바보로 느껴질 수 있습니다.

1. 극한과 연속성의 의미

2. 적분법의 의미

[그림 1] 디랙 델타 함수의 개념적 정의(출처: wikipedia.org)

디랙 델타 함수(Dirac delta function)는 좌표계(coordinate system) 상에서 점(點, point)을 정의하기 위해 사용한다. 여러 수학자가 비슷한 개념을 사용했지만 1927년디랙 25세, 일제 식민지 시절에 디랙Paul Dirac(1902–1984)이 쓴 양자 역학(量子力學, quantum mechanics) 책이 유명해져서 델타 함수의 이름에 디랙이 붙게 되었다.[디랙이 델타 함수를 처음 사용한 해는 1926년이다.] 디랙은 행렬 이론(matrix theory)에 등장하는 식 (1)의 크로네커 델타(Kronecker delta)의 연속 함수(continuous function) 형태가 디랙 델타 함수라 생각해서 이와 같은 이름을 붙였다.

                       (1)

예를 들어 1차원 좌표계 상에서는 개념적으로 [그림 1]처럼 점을 생각할 수 있다. [그림 1]을 좀더 수학적으로 표현하면 다음과 같다.

                       (2a)

                       (2b)

점을 표현하기 위해서라면 $x$ = $0$이라 하면 되지 않나? 식 (2a)는 점을 표현하기에는 너무 복잡해 보인다. 하지만, 디랙 델타 함수를 사람들이 왜 쓰는가를 봐야한다. 디랙 델타 함수는 미분 방정식(differential equation)을 풀기 위해 사용한다. 미분 방정식에 합당한 디랙 델타 함수를 잘 정의해야 문제를 풀 수 있기 때문에, $x$ = $0$과 같은 초보적인 정의는 별의미가 없다. 식 (2b)는 디랙 델타 함수의 특성을 고려하면 당연하다. 디랙 델타 함수는 $x$ = $x'$인 경우에만 값이 존재하므로 $x, x'$를 바꾸더라도 값은 서로 같다.[∵ $x$ = $x'$와 $x'$ = $x$는 서로 동일하다.] 또한 식 (2a)의 정의는 수학자가 좋아하는 표현식이 아니다. 왜냐하면, 무한대가 들어가기 때문이다. 잘 알 듯이 무한대는 숫자가 아니고 수가 커져가는 상태이기 때문에 식 (2a)로 정의하면 디랙 델타 함수를 명확하게 정의할 수는 없다. 그래서 아래와 같은 적분 정의가 제대로된 델타함수 정의이다.

                       (3)

수학자들이 식 (3)을 좋아하는 이유는 무엇일까? 바로 적분을 이용해 점을 표현하기 때문이다. 이 특성을 바탕으로 미분 방정식의 해를 손쉽게 구한다. 이런 방식의 미분 방정식 풀이법은 그린 함수(Green's function) 방법이라 부른다. 예를 들면 임의의 함수 $f(x)$는 식 (3)의 양변에 $f(x)$를 곱해서 아래처럼 적분으로 표현할 수 있다.

                 (4)

여기서 $\delta(x-x')$는 식 (2a)의 정의에 의해 $x$ = $x'$에서는 무한대이고 $x$ $\ne$ $x'$이면 0인 디랙 델타 함수이다. 함수 $\delta(x-x')$는 $x$ = $x'$에서만 값을 가지므로, $f(x) \delta(x-x')$ = $f(x') \delta(x-x')$가 되어서 식 (4)가 증명된다.[∵ $x \ne x'$인 경우는 $\delta(x-x')$이 0이므로 $f(x)$에 관계없이 항상 같다.]

처음부터 수학자들이 디랙 델타 함수를 환영하지는 않았다. 폰 노이만John von Neumann(1903–1957)과 같은 저명한 수학자는 디랙 델타 함수를 망상(fiction)이라 폄하했으며, 양자 역학은 디랙 델타 함수와 같은 이상한 함수를 사용하지 않고도 명확하게 공식화할 수 있다고 강조했다[1]. 이러한 이유로 물리학자는 디랙 델타 함수가 편리하기 때문에 계속 사용하고, 수학자는 함수 정의가 이상하기 때문에 거부하는 애매한 상태가 지속되었다. 디랙 델타 함수에 대한 물리학과 수학 사이의 간극을 적극적으로 고민한 수학자는 슈바르츠Laurent Schwartz(1915–2002)이다[1]. 슈바르츠는 디랙 델타 함수를 비판하기보다 새로운 수학적 실체로 인식하였다. 디랙 델타 함수에 함수란 이름이 붙어있지만, 함수 정의에 의하면 디랙 델타 함수는 함수가 아니다.[$\because$ 특정한 점에서 함수가 발산하기 때문에 공역의 원소를 특정할 수 없다. 쉽게 말하면 특정한 점에서는 계산 불능이다.] 이 점이 수학자들의 주요 비판꺼리였다. 슈바르츠는 함수가 아니라고 부정하는 대신, 디랙 델타 함수는 함수의 일반화이며 새로운 실체라고 정확히 인식하였다.

이러한 인식의 결과물이 슈바르츠가 제안한 분포(distribution)란 개념이다. 분포는 함수(function)와 비슷하지만 정의역에서 차이가 난다. 함수의 정의역은 숫자이지만, 분포의 정의역은 구간이다. 이 구간을 정의하기 위해 함수를 정의역으로 택할 수도 있기 때문에, 분포는 범함수(functional: 정의역의 원소인 어떤 함수에서 실수나 복소수로 가는 사상)로 생각할 수 있다. 이 부분은 어려운 이야기 같지만, 식 (4)의 최종 결과식이 의미하는 바이다. 정의역이 구간이기 때문에, 분포 정의에서는 무한대 개념을 피할 수 있다. 또한 구간을 0으로 보내면 분포 정의는 함수 정의와 동일해진다. 좀 더 적극적으로 식 (3)을 보면, $x = 0$ 근방에서는 적분 구간을 어떻게 정의하더라도 적분값은 1이 됨을 알 수 있다. 따라서 분포 개념은 해당 구간에 함수값이 어떻게 배치되는지를 뜻하기 때문에, 수학적 이름은 당연히 분포가 되었다. 

다른 측면으로 분포는 다양한 함수를 정의하는 새로운 방법이다. 통상적인 함수는 적분해서 구간을 바꾸면 적분값이 당연히 달라진다. 하지만 디랙 델타 함수는 적분 구간을 줄이든 혹은 늘리든 $x$가 구간 안에만 있으면 적분값은 1로 고정된다. 이런 이상한 성질을 가진 함수를 정적분으로 정의하는 개념이 분포이다. 푸리에 변환의 완비성을 뜻하는 식 (20)도 마찬가지 방식으로 설명한다. 식 (20)의 피적분 함수는 지수 함수이므로, 이 정적분 자체는 어렵지 않다. 하지만 우리가 선택하는 적분 구간에 따라 적분값이 달라져서 구간이 무한대로 가는 적분은 정의되지 않는다. 그래서 식 (20)을 한 번 더 적분함으로써 그 결과를 하나로 정할 수 있어서, 식 (20)은 분포의 좋은 예가 된다. 이와 같이 분포라는 새로운 수학적 정의로 인해 디랙 델타 함수는 빠르게 수학 영역으로 들어오게 되었다. 이런 획기적인 분포 개념을 제안한 슈바르츠는 1950년슈바르츠 35세, 이승만 정부 시절에 수학의 노벨상이라는 필즈 메달(Fields Medal)을 받게 된다. 슈바르츠가 받은 필즈 메달은 프랑스 최초의 필즈 메달이었다.

디랙 델타 함수를 식 (2a)나 (3)으로 정의할 수 있는 연속 함수는 잘 떠오르지 않는다. 그래서 델타 함수를 정의할 때는 [그림 2]처럼 항상 극한(limit) 개념을 사용해서 정의한다.

[그림 2] 극한을 이용한 디랙 델타 함수 정의(출처: wikipedia.org)

극한을 이용해서 디랙 델타 함수를 정의한다는 의미는 디랙 델타 함수를 만들 수 있는 극한이 하나가 아니고 여러 경우가 있을 수 있다는 뜻이다. 따라서, 아래에 디랙 델타 함수 정의인 식 (3)을 만족할 수 있는 다양한 예들을 소개한다. 단순히 생각하면 디랙 델타 함수는 식 (3)의 성질을 가진 함수를 표현하기 위한 일종의 표기법이 된다. 수학적으로 디랙 델타 함수는 분포 혹은 일반화 함수(generalized function)의 아주 좋은 예가 된다.

[그림 3] 구형 함수(출처: wikipedia.org)

[구형 함수 혹은 사각 함수 이용한 정의]

                       (5)

[증명]

[그림 3]의 구형 함수(矩形函數, rectangular function) 혹은 사각 함수는 아래처럼 정의한다.

                       (6)

구형 함수의 면적은 $1$이기 때문에, 상수 $a$만 잘 곱하면 식 (5)를 증명할 수 있다. 식 (6)에 의해 $a|t|$ = $1/2$이 되는 값은 $t$ = $\pm 1/(2a)$가 된다. 그래서, ${\rm rect}(t)$ = $1$이 되는 구간 길이는 $1/a$가 된다. 만약 $a$가 무한대로 가면, $1$이 되는 구간은 $0$이 되기 때문에 식 (3)의 정의 중 일부가 만족된다. 또한 식 (3)에 의해 구형 함수의 적분값[혹은 면적]이 $1$이 되어야 하므로, 이 결과에 $a$를 곱하면 식 (5)가 증명된다.

______________________________

구형 함수 정의인 식 (6)은 좀 인위적인 냄새가 난다. 그래서, 연속 함수의 극한으로 식 (6)을 다시 정의해보자.

                       (7)

변수 $t$에 구체적인 숫자를 넣어 극한을 취해보면 식 (7)과 (6)이 동등함을 쉽게 보일 수 있다. 그러면 디랙 델타 함수를 좀더 예쁘게 정의할 수 있다.

                       (8)

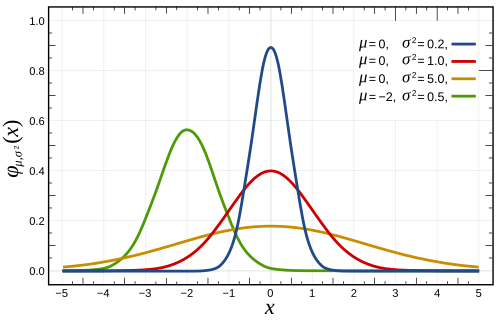
[그림 4] 가우스 함수(출처: wikipedia.org)

[가우스 함수 이용한 정의]

                       (9)

[증명]

가우스 함수(Gaussian function)의 아래 특성을 이용해 디랙 델타 함수를 정의해보자.

                       (10)

식 (10)에서 변수 치환을 하면 아래를 얻을 수 있다.

                       (11)

상수 $a$가 $0$으로 접근하면 $x \ne 0$에서는 함수값이 0이 되고 $x$ = $0$에서는 발산해서 식 (3)의 정의를 만족한다.

______________________________

[그림 5] 표본화 함수(출처: wikipedia.org)

[표본화 함수 이용한 정의]

                       (12)

[증명: 푸리에 변환쌍]

표본화 함수(sampling function) ${\rm Sa}(\cdot)$의 적분은 매우 까다로우므로[원칙대로 적분을 할 때는 조르당의 보조 정리(Jordan's lemma)를 사용한다.], 아래의 푸리에 변환쌍(Fourier transform pair)을 먼저 고려하자.

                       (13)

식 (6)에 정의된 구형 함수의 푸리에 변환은 표본화 함수가 된다. 이를 이용해 표본화 함수의 적분을 구하면 다음과 같다.

                       (14)

여기서 [그림 3]에 따라 ${\rm rect}(0)$ = $1$이다. 식 (14)의 결과에 변수 치환[$t \to at$]을 하면 아래를 얻을 수 있다.

                       (15)

식 (15)는 상수 $a$에 관계없이 성립하므로 $a$를 무한대로 보내보자. 그러면 $t$ = $0$인 점에서는 발산함을 볼 수 있다.

[증명: 푸리에 변환의 완비성]

식 (20)의 적분으로부터 다음이 성립한다.

                       (16)

______________________________

식 (12)는 엄밀한 의미에서 디랙 델타 함수는 아니다. 디랙 델타 함수가 되려면 $t \ne 0$ 영역에서 0이 되어야 하지만 $t$가 무한대로 가는 경우를 제외하고는 식 (12)가 0이 되지는 않는다. 하지만 식 (12)는 식 (4)를 아래와 같이 만족한다.

                       (17)

그래서 식 (12)와 같은 종류의 디랙 델타 함수를 발생기 델타 함수(發生期, nascent delta function)라 부른다. 발생기 델타 함수는 디랙 델타 함수를 정의하기 위한 극한을 취하기 전에는 식 (3)이 성립하지 않지만 극한을 취함으로써 식 (3)이 성립하여 디랙 델타 함수가 된다는 의미다. 예를 들면, 식 (11)과 (15)는 식 (3)과 닮아있지만 극한을 취하지 않아 $t \ne 0$ 영역에서 0이 되지 않는다. 비슷하게 식 (12)도 $t \ne 0$ 영역에서 0이 되지 않지만 식 (4)가 성립하기 때문에 발생기 델타 함수라 할 수 있다. 디랙 델타 함수는 어차피 미분 방정식을 풀기 위해 사용하므로 발생기 델타 함수를 사용하더라도 대세에는 지장이 없다.

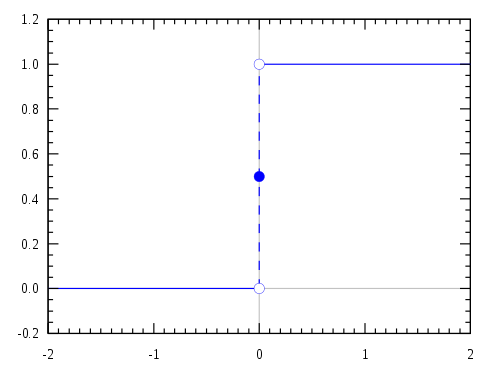
[그림 6] 단위 계단 함수(출처: wikipedia.org)

[단위 계단 함수 이용한 정의]

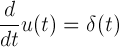                       (18)

[증명]

단위 계단 함수(unit step function)는 제안자 이름을 따라 헤비사이드 계단 함수(Heaviside step function)라고 하기도 한다. 함수 이름이 거창하지만 특성은 [그림 6]처럼 단순하다. 식 (18)을 식 (3)에 넣어 계산해보자.

                       (19)

[그림 6]을 참고하면 단위 계단 함수의 미분은 $t$ = $0$ 지점을 제외하고는 모두 0이므로 식 (3)을 정확히 만족한다.

______________________________

[푸리에 변환 이용한 정의]

                       (20)

[증명]

푸리에 변환의 완비성(completeness of Fourier transform)으로 쉽게 증명 가능하다.

______________________________

[한켈 변환 이용한 정의]

                       (21)

[증명]

한켈 변환의 특성(Hankel transform)으로부터 증명한다.

______________________________

식 (21)에서 $n$은 $\phi$방향 변화를 의미한다. 즉, $\phi$방향으로 $n$번 바뀌는 함수는 $e^{in\phi}$이므로, 방위각 함수 $e^{in\phi}$에 대한 디랙 델타 함수는 식 (21)로 표현된다.

[고유 함수의 무한 급수로 정의]

                      (22)

여기서 $\psi_m (x)$는 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)의 정규 직교 고유 함수(orthonormal eigenfunction)이다.

[증명]

고유 함수의 완비성(completeness of eigenfunctions)에 의해 증명 가능하다.

______________________________

[푸리에 급수 이용한 정의]

                  (23)

[증명]

푸리에 급수(Fourier series)도 고유 함수이므로 식 (22)를 이용해 증명 가능하다. 아니면 푸리에 급수의 완비성(completeness of Fourier series)을 이용해도 된다. 푸리에 급수 증명에 디리클레 핵심(Dirichlet kernel)이 사용되므로 식 (23)을 다음처럼 표현할 수도 있다.

(24)

______________________________

[한켈 함수 이용한 정의]

                      (25)

여기서 $y$는 항상 0보다 크다.

[증명]

식 (25)를 보면 분자에 $y$가 있기 때문에 $x \ne x'$인 경우 전체 값이 0이 되는 건 자명하다. 따라서 한켈 함수(Hankel function) 특성을 이용해 $x \approx x'$ 근방에서 $x$에 대해 적분을 해보자.

                      (26)

식 (25)의 두번째 줄을 적분한 값은 식 (26)에 의해 1이므로 디랙 델타 함수 정의에 의해 식 (25)가 항상 성립한다.

______________________________

식 (25)에서 $y$가 항상 0보다 작은 상태에서 0으로 간다면 특이하게 다음처럼 디랙 델타 함수의 부호가 바뀐다.

                      (27)

[2차 함수의 역수 이용한 정의: 로렌츠–코쉬 함수(Lorentz–Cauchy function) 혹은 룽에 함수(Runge function)]

                      (28)

[증명]

식 (26)에 제시한 적분을 이용해 식 (28)을 증명한다. 

______________________________

[브롬위치 적분 이용한 정의]

                      (29)

여기서 $\sigma$는 복소 적분을 수렴시키는 임의의 실수이다.

[증명]

라플라스 역변환(inverse Laplace transform)에 해당하는 브롬위치 적분(Bromwich integral)으로 증명한다.

______________________________

[멜린 변환 이용한 정의]

                  (30)

여기서 $\Re[s]$ = $\Re[u]$이다.

[증명]

멜린 변환(Mellin transform)과 역변환(inverse transform) 관계에서 얻어지는 중요한 결과이다.

______________________________

[멜린 역변환 이용한 정의]

                  (31)

[증명]

원칙적으로는 멜린 역변환(inverse Mellin transform)과 복소 함수론(complex analysis)으로 증명한다. 푸리에 변환과 관계된 식 (20)을 이용해서도 다음처럼 유도할 수 있다.

                  (32)

여기서 $t > 0$, $t' > 0$이다. 식 (32)의 최종 결과에 식 (1.4)를 적용해서 식 (31)을 얻는다.

                  (33)

______________________________

[그림 7] 반원 상의 복소 적분을 위한 닫힌 경로(출처: wikipedia.org)

[반원 상의 푸리에 변환 이용한 정의]

                       (34)

여기서 $R$은 [그림 7]에 있는 반원의 반지름이다.

[증명]

복소 지수 함수는 전영역에서 극점이 없으므로, 코쉬의 적분 정리에 의해 [그림 7]의 닫힌 경로를 도는 복소 적분은 $0$이다. 따라서 적분 방향을 바꾸어서 정리하면 식 (34)를 얻는다.

                       (35)

여기서 $c_2$에 대한 적분은 식 (20)과 같다.

______________________________

식 (12)와 (34)를 변형해서 복소 지수 함수의 지수가 무한대로 가는 새로운 극한값을 유도할 수 있다.

                  (36)

식 (36)의 마지막 줄과 식 (34)를 비교하면 다음 관계식을 얻는다.

                       (37)

여기서 $0 \le \phi \le \pi$이다.

[그린 함수 이용한 정의]

                     (38: 이산적 고유치)

                     (39: 연속적 고유치)

여기서 $g(x, x'; \lambda)$는 그린 함수(Green's function), $\lambda$는 미분 방정식의 고유치(eigenvalue), $\psi_m(x)$는 제$m$번 고유 함수(eigenfunction), $r(x)$는 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)에 나오는 함수, $c$는 그린 함수의 모든 극점을 포함하는 닫힌 경로, $c_R$은 연속적 고유치를 모두 포함하는 원형인 열린 경로이다.

[증명]

그린 함수의 정의를 이용하여 증명한다.

______________________________

[콘토로비치–레베데프 변환 이용한 정의]

                       (40a)

                       (40b)

[증명]

식 (39)를 콘토로비치–레베데프 변환(Kontorovich–Lebedev transform)에 적용하면 쉽게 증명된다.

______________________________

[베버 변환 이용한 정의]

                  (41)

                   (42)

[증명]

식 (41)과 (42)는 각각 접선과 법선에 대한 베버 변환(Weber transform)과 관계되므로, 자연스럽게 적분과 디랙 델타 함수가 서로 연결된다.

______________________________

[푸리에 사인 및 코사인 변환 이용한 정의]

                       (43)

                       (44)

[증명]

식 (43)과 (44)는 바로 푸리에 사인 및 코사인 변환(Fourier sine and cosine transforms)의 완비성(completeness)이다.

______________________________

[르장드르 함수 이용한 정의]

                      (45)

[증명]

르장드르 함수(Legendre function) $P_n(\cos \theta)$는 고유 함수이므로, 식 (22)에 의해 식 (45)가 쉽게 증명된다. 여기서 $(2n+1) \mathbin{/} 2$는 $P_n(\cos \theta)$를 자기 자신으로 내적할 때에 나오는 상수의 역수, $x$ = $\cos \theta$의 미분은 $dx$ = $-\sin \theta d \theta$라서 식 (45)의 좌변에 $\sin \theta$가 나온다.

______________________________

[구면 조화 함수 이용한 정의]

                      (46)

[증명]

식 (23)에 따라 구면 조화 함수(spherical harmonics) $Y_n^m(\theta, \phi)$의 무한 수에는 $\phi$에 대한 디랙 델타 함수 $\delta(\phi - \phi')$가 숨어있다.

                      (47)

식 (46)의 좌변에서 디랙 델타 함수 $\delta(\phi - \phi')$를 묶어내고 나머지 항을 보면,  르장드르의 미분 방정식(Legendre's differential equation)의 고유 함수 $P_n^m(\cos \theta)$가 나온다. 계수 $m$을 고정한 $P_n^m(\cos \theta)$는 다시 식 (23)에 의해 새로운 디랙 델타 함수 $\delta(\theta - \theta')$를 생성한다.

                      (48)

여기서 무한 급수 안에 있는 상수는 $P_n^m(\cos \theta)$의 내적을 1로 만드는 상수이다. 다만 $|m| > n$을 만족하는 $P_n^m(\cos \theta)$는 0이라서, 식 (46)에 나온 계수 $m$은 $-n \le m \le n$만 택해서 공식화한다.

______________________________

식 (3)에 있는 디랙 델타 함수의 정의를 이용하면 분포(distribution) 관점으로 다양한 디랙 델타 함수의 성질을 증명할 수 있다.

 

   1. 기본(basics)   

[분포적 성질]

                  (1.1: 대칭성)

                  (1.2: 비율 조정)

[증명]

식 (3)에 식 (1.2)를 대입하고 식 (1.1)을 적용해서 적분한다.

                  (1.3)

______________________________

                  (1.4: 함수의 영점)

여기서 $x_k$는 $f(x)$의 $k$번째 영점(zero), $f'(x)$는 $f(x)$의 미분이다.

[증명]

함수 $f(x)$의 영점 $x_k$ 근처에서 다음처럼 디랙 델타 함수에 대한 적분을 한다.

                  (1.5)

여기서 $f(x)$는 $x_k$ 근처에서 선형적으로 변하며, $\Delta$는 매우 작은 양의 실수, $\Delta_t$는 $t$ = $f(x)$ 치환에 대한 $\Delta$의 변화량이다. 영점 $x_k$에 $f(x)$가 접하는 경우는 식 (1.1)을 기반으로 변수 치환해서 식 (1.5)와 비슷하게 적분한다.

                  (1.6)

함수 $f(x)$의 다른 영점에 대해서도 동일한 개념을 이용해서 식 (1.4)를 얻는다.

______________________________

식 (1.4)를 이용해서 식 (1.2)를 유도할 수도 있다.

                  (1.7: 미분)

[증명]

식 (1.7)의 첫째식에 대해 부분 적분을 한다.

                  (1.8)

식 (1.7)의 첫째식을 여러 번 적용해서 식 (1.7)의 둘째식을 얻는다.

______________________________

디랙 델타 함수의 미분은 특이하게도 함수 $f(x)$의 미분 연산자로 작용한다.

[참고문헌]

[1] N. Wheeler, "Simplified production of Dirac delta function identities," Reed College, USA, Nov. 1997. (방문일 2011-10-13)

[2] 최인혁, "해석학하는 만화 [6]: 디랙 델타…??", HORIZON, 2019년 11월. (방문일 2020-02-29)

[다음 읽을거리]
1. 그린 함수