[경고] 아래 글을 읽지 않고 "단위 계단 함수의 푸리에 변환"을 보면 바보로 느껴질 수 있습니다.
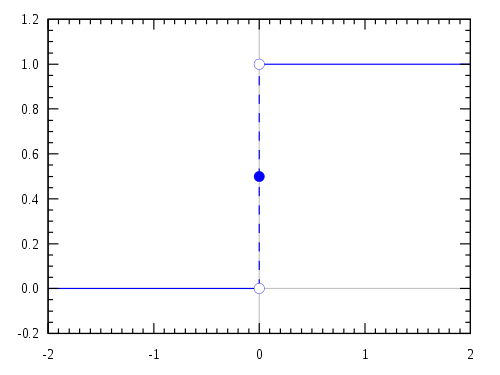
[그림 1] 단위 계단 함수(출처: wikipedia.org)
단순함 속에 존재하는 심오함을 느끼고 싶으면, 일단 한번 단위 계단 함수(unit step function)를 사색하라. 푸리에 변환(Fourier transform)을 넘어서 라플라스 변환(Laplace transform)으로 가는 열쇠가 다음에 정의하는 단위 계단 함수 $u(t)$에 있다.
 (1)
(1)단위 계단 함수는 제안자 헤비사이드Oliver Heaviside(1850–1925) 이름을 따서 헤비사이드 계단 함수(Heaviside step function)라고도 한다. 헤비사이드는 단위 계단 함수에 대한 고민을 통해 19세기 수학 분야의 논란거리였던 라플라스 변환을 제안하고 미분 방정식(differential equation)을 푸는 새로운 방법론을 제안했다. 언뜻 봐서는 식 (1)에 제시한 단위 계단 함수의 정의가 너무 간단해서 새로움을 찾기는 어렵다. 그런데 어떻게 단위 계단 함수가 라플라스 변환까지 연결될 수 있을까? 단위 계단 함수의 오묘함을 느끼기 위해 푸리에 변환을 이용해 식 (1)을 적분해보자.
 (2)
(2)무한대로 가는 극한을 취하기 전까지 식 (2)는 잘 정의된다. 하지만 $T \to \infty$라면, 식 (2)는 진동하기 때문에 적분이 정해지지 않는다. 어떻게 해야 식 (2)의 적분을 정할 수 있을까? 단순한 푸리에 변환 관점에서는 진동하는 적분값을 절대 고정할 수 없다. 그래서 강제로 감쇠(減衰, attenuation) $\sigma$를 주어서 식 (2)의 적분을 수렴하게 한다. 이후에 감쇠를 $0$으로 보내는 극한[$\sigma \to 0^+$]을 적용한다. 이런 접근법이 푸리에 적분을 진화시킨 라플라스 변환의 중요한 특징이다.

[그림 2] 부호를 바꾸면서 양방향으로 감쇠하는 지수 함수
식 (2)의 적분을 정하는 표준적인 방법은 부호 함수(sign function) $\operatorname{sgn}(t)$[= $2u(t)-1$]에 [그림 2]와 같은 감쇠를 주고 적분하기이다. 변수 $t \to \pm \infty$로 갈 때 [그림 2]의 함수는 $0$으로 수렴하기 때문에 안정된 적분이 가능하다.
 (3)
(3)여기서 $\mathfrak{F}[f(t)]$는 $f(t)$의 푸리에 변환, $\sigma$는 임의의 작은 양의 실수이다. 식 (3)에서 $\sigma \to 0^+$로 보내면, 부호 함수의 푸리에 변환을 쉽게 얻을 수 있다.
 (4)
(4) (5)
(5)여기서 $\delta(\omega)$는 디랙 델타 함수(Dirac delta function)이다.

[그림 3] 단방향으로 감쇠하는 지수 함수
부호 함수에 감쇠를 줄 수 있다면, 단위 계단 함수에도 [그림 3]처럼 감쇠를 추가해서 식 (5)를 얻을 수 있을까? 식 (3)과 동일한 방법으로 푸리에 변환을 위한 적분을 유도한다.
 (6)
(6)식 (6)의 감쇠 $\sigma$를 $0$으로 보내면 적분값은 $1/(i \omega)$가 나온다. 이 결과는 식 (5)와 비슷하지만 디랙 델타 함수는 사라졌다. 어디에서 문제가 생겼을까? 식 (6)에서 마지막식의 분모를 보자. 분모를 구성하는 $\sigma$와 $\omega$가 모두 $0$이 된다면, 분모도 역시 $0$이 되어서 적분 계산에 문제가 생긴다. 그래서 식 (6)을 다음처럼 변형해야 한다.
 (7)
(7)식 (7)에서 극한을 적용할 때, 식 (8)과 같은 디랙 델타 함수가 나오도록 분모를 변형해서 유도하니까 식 (5)와 동일한 결과가 나온다.
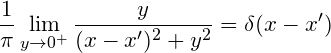 (8)
(8)정답을 얻었다는 안도감이 있으면서 왠지 모를 거북함도 느껴진다. 분명 우리가 얻은 단위 계단 함수의 푸리에 변환은 타당하다. 그렇지만 극한을 사용하는 과정에서 답을 보고 과정을 끼워맞춘 것 같기도 하다. 이런 애매함의 근원이 바로 푸리에 변환의 한계이다. 푸리에 변환은 $t$가 커질수록 복소 지수 함수(complex exponential function)를 빠르게 진동시켜서 적분을 구한다. 이런 푸리에 변환 과정은 단위 계단 함수나 부호 함수의 적분에는 적합하지 않다. 식 (2)의 결과에서도 보듯이 $t$가 무한대로 갈 때 함수값이 남아있는 함수는 푸리에 변환의 적분이 수렴하지 않고 계속 진동한다. 그래서 우리가 얻는 식 (7)은 식 (2)의 적분값이 아니다. 식 (2)에서 $T$가 커질 때, 적분 결과는 계속 진동하므로 식 (2)는 적분 불능이 답이다. 반면에 식 (7)은 식 (2)의 적분에 대한 수학적으로 타당한 극한이다. 적분이 존재하지 않아서 타당한 수학적 추론으로 적분의 극한을 정의했기 때문에, $u(t)$의 푸리에 변환을 식 (7)처럼 쓸 수 있다. 이러한 혼란을 군더더기 없이 편하게 해결할 수 있을까? 우리는 푸리에 변환의 멋진 해결책을 이미 경험했다. [그림 2, 3]처럼 강제적으로 감쇠 $\sigma$를 더하면 적분이 잘 된다. 감쇠를 이용해 얻어진 적분은 감쇠를 남겨두어도 된다. 애매한 극한 연산인 $\sigma \to 0^+$를 할 필요가 없다. 예를 들어, 식 (6)에서 $s$ = $\sigma + i \omega$로 정하자. 그러면 $u(t)$의 감쇠 있는 푸리에 변환을 다음처럼 정확히 쓸 수 있다. 다시 강조하지만 적분 후에 극한을 취할 필요가 없다.
 (9)
(9)식 (9)는 $u(t)$의 라플라스 변환과 완전 동일하다. 푸리에 변환처럼 감쇠의 극한 특성을 고민할 필요 없이 원래부터 감쇠가 있다고 가정하면 적분이 정말 편해진다. 따라서 감쇠를 버리지 않고 남기는 푸리에 변환에는 새로운 이름이 필요하다. 바로 라플라스 변환이 그 이름이다.

[그림 4] 단위 계단 함수를 위한 복소 평면 상의 적분 경로
복소 함수론(complex analysis)을 이용해 복소 평면(complex plane)에서 닫힌 선 적분(line integral)을 하면, 식 (7)의 증명 과정을 수학적으로 더 엄밀하게 만들 수 있다. 먼저 식 (2)를 바탕으로 복소 평면 상의 적분을 정의한다. 복소 지수 함수 $e^{-i\omega z}$는 [그림 4]와 같은 적분 경로 $c_1 + c_2 + c_3$ 혹은 $c_4 + c_5 + c_6$ 내부에 극점(pole)을 가지지 않으므로 코쉬의 적분 정리(Cauchy's integral theorem)가 성립한다. 이를 바탕으로 $\omega > 0$에 대한 $u(t)$의 복소 적분(complex integral)을 얻는다.
 (10)
(10)여기서 $R$이 무한대로 갈 때 경로 $c_2$ 상에서 $e^{-i\omega z}$는 $0$이다. 식 (10)에서 $c_2$가 범위인 적분 $I_2(\omega)$[= $\int_{c_2} e^{-i \omega z}\,dz$]는 정적분이 되지 않으므로, 디랙 델타 함수의 정의에 쓰는 분포(distribution) 개념에 따라 $\omega$에 대해 적분해 $I_2(\omega)$ = $0$임을 확인한다. 즉, $I_2(\omega)$를 적분하면 $\int_\alpha^\beta I_2(\omega)\,d\omega$ = $\int_{c_2} (e^{-i\alpha z} - e^{-i\beta z}) \mathbin{/} (iz)\,dz$처럼 분모에 $z$가 나타난다. 이 최종 적분에 조르당의 보조 정리(Jordan's lemma)를 응용해 0을 얻고, 다시 복소 적분의 영인자(nullity of complex integration)를 써서 $I_2(\omega)$ = $0$을 유도한다. 이러한 방식은 푸리에 변환의 완비성 증명에도 동일하게 사용된다.
마찬가지로 $\omega < 0$인 경우에는 경로 $c_4 + c_5 + c_6$을 택해야 $R$이 커짐에 따라 $e^{-i\omega z}$가 $c_5$ 상에서 $0$으로 간다. 따라서 $u(t)$의 복소 적분을 다음처럼 얻는다.
 (11)
(11)결국 $\omega \ne 0$이라면, $u(t)$의 푸리에 변환은 $1/(i \omega)$가 된다. 다음으로 $\omega$ = $0$ 근방의 적분 특성을 얻기 위해 식 (2)를 $\omega$에 대해 한 번 더 적분한다.
 (12)
(12)여기서 $\Delta$는 임의의 작은 양의 실수이다. 식 (12)에서 $\Delta$는 한없이 작아질 수 있기 때문에, $\omega$ = $0$ 근방에서 식 (2)의 적분은 $\pi \delta(\omega)$이다. 최종적으로 식 (10)–(12)의 결과를 합쳐서 식 (7)을 얻는다.
식 (2)와 (5)를 연립하면, 분포(distribution) 관점으로 삼각 함수의 새로운 극한값을 결정할 수 있다.
 (13)
(13) (14)
(14)라플라스 변환인 식 (9)의 관점을 단위 계단 함수 $u(t)$로 바꾸어서 다음과 같은 적분을 정의하기도 한다.
 (15)
(15)단위 계단 함수의 푸리에 변환인 식 (5)를 사용해서 반무한 적분 구간을 가진 삼각 함수의 푸리에 변환과 이상 적분(improper integral)을 각각 유도할 수 있다.
 (16)
(16) (17)
(17)특이하게도 삼각 함수의 곱을 반무한 적분하면, 최종 결과에서 디랙 델타 함수는 사라지고 주파수가 높아지면 $1/\omega^2$ 혹은 $-1/\omega$ 형태로 0에 접근하는 로렌츠–코쉬 함수(Lorentz–Cauchy function) 혹은 룽에 함수(Runge function) 형태를 가진다. 라플라스 변환처럼 식 (16)에서 $\omega$를 복소수라 가정해서 $\lim_{t \to \infty}e^{-i \omega t}$ = $0$으로 두면, 이상 적분의 답은 매우 간단해진다.
 (18)
(18)여기서 $\Im[\omega] < 0$, $\omega$는 복소수라서 $\pm \omega_0$과 같아질 수 없어서 디랙 델타 함수는 항상 0이 된다.
[다음 읽을거리]
10번 이미지에서 c2 경로적분은 왜 0이 되는건가요 조르당의 보조정리로는 설명이 되지않습니다 그냥 전개해보니 R * exp(-Rsinx)형태가 나오는데 이러면 각도 x가 0이 아닐때에 한해서 경로적분이 0이될듯한데 그건 따로 적분범위에 극한을 취해 보여줘야할까요 아니면 경로 C2가 z=R을 포함하지 않아 괜찮나요?
답글삭제말씀하신대로 조르당의 보조 정리(Jordan's lemma)로는 그 적분값이 유한하다는 정도만 알 수 있어요. 설명이 부족한 듯 해서 식 (10) 밑에 설명을 조금 추가했어요.
삭제