[경고] 아래 글을 읽지 않고 "등방성 안테나의 불가능성"을 보면 바보로 느껴질 수 있습니다.

[그림 1] 한 방향으로 빗질한 털공(출처: wikipedia.org)
전자기학은 물리학의 일부이고, 물리학은 수학이란 도구로 기술된다. 그리하여 자연계를 설명하는 근원은 수학보다는 물리학일 수 있다. 이런 평범한 관념을 무너뜨리는 재미있는 개념 중에 등방성 안테나(isotropic antenna)가 있다. 등방성 안테나는 모든 방향으로 전자파 전력을 골고루 복사시켜서 방향도(directivity) 혹은 안테나 이득(antenna gain)을 1 혹은 0 dBi로 만든 안테나이다. 그러나 우리가 안테나 설계를 아무리 잘 하더라도 등방성 안테나를 만들 수 없다[1]. 등방성 안테나의 불가능성(impossibility of isotropic antenna)은 물리학이 아니고 벡터 함수(vector function) 혹은 벡터장(vector field)에 대한 수학으로 설명해야 한다. 그래서 물리학을 도와주는 수학이 아니고, 물리학의 한계를 엄격히 제한하는 우리 사고의 틀로서의 수학을 등방성 안테나에서 만날 수 있다. 물론 물리학과 수학의 관계에 대해서는 다양한 관점이 존재할 수 있다. 하지만 등방성 안테나의 불가능성은 전자기학이 속한 물리학보다 벡터(vector)를 다루는 수학이 더 근원적이며 물리학에 앞서 수학이 실존한다는 증거일 것이다.

[그림 2] 스칼라 함수의 권선수(출처: wikipedia.org)
등방성 안테나가 불가능한 이유는 전자기파가 편파(polarization) 혹은 벡터 특성을 가지기 때문이다. 더 원초적 이유는 벡터 함수의 권선수(winding number) 성질 때문이다[2], [3]. 권선수는 스칼라(scalar) 혹은 벡터 함수가 닫힌 곡선(closed curve)의 반시계 방향을 따라 돈 회수라서 항상 정수로 나온다. [그림 2]처럼 스칼라 함수의 권선수는 우리가 선택한 곡선의 회전수로 헤아리면 된다. 닫힌 곡선 $c$에 대한 권선수 $W(c)$는 다음과 같이 정의한다.
 (1)
(1)여기서 $\phi_c(s)$는 극형식(polar form)으로 결정한 $c$의 연속적 편각(argument)[예를 들어, $2 \pi$를 0으로 바꾸지 않고 계속 증가시킨다.], $s$는 $c$에 대한 호의 길이(arc length), $c$는 $s$ = $0$에서 시작하고 $s$ = $1$에서 마치며, $c$는 닫힌 곡선이라서 $s$ = $0$과 $1$은 3차원 공간 $\mathbb{R}^3$에서 같은 위치를 가리킨다. 특정점 $\bar p$에 대한 권선수는 $W(c; \bar p)$로 표현한다. 이때 $c$의 편각 $\phi_c$는 위치 벡터(position vector) $\bar R(s)$로 헤아린다.
 (2a)
(2a)여기서 $\bar R$ = $\bar r(s) - \bar p$; $\bar r(s)$는 $c$상의 $s$에 대응하는 3차원 점이다. 만약 $\bar p$가 곡선의 바깥에 있으면, 편각은 한 바퀴를 온전히 채우지 못해서 항상 $W(c; \bar p)$ = $0$이다. 점 $\bar p$가 내부점이면, 닫힌 곡선의 모양에 따라 권선수는 $\pm 1, \pm 2$ 등이 될 수 있다.

[그림 3] 벡터 함수의 지표: 초록색 점은 중심점(center or center point), 빨간색 점은 안장점(saddle or saddle point)(출처: wikipedia.org)
[곡선의 지표 이론(index theory on curves)]
스칼라 함수와 다르게 벡터 함수의 권선수는 정의하기가 까다롭다. 식 (1)을 벡터 함수에도 적용하려면, $\phi_c(s)$가 구성되는 원리를 더 확장해야 한다. 고정된 기준 단위 벡터(reference unit vector) $\hat e_r$에 대해 $\phi_c(s)$를 벡터 내적으로 재정의한다.
 (2b)
(2b)여기서 $\hat v(s)$는 벡터 함수의 $s$에 딸려 존재하는 벡터 $\bar v(s)$의 단위 벡터[그림 3에서 화살표]이다. 벡터 함수의 권선수 $W(c; \bar p)$와 [그림 3]에 보인 이산적인 고립된 특이점(isolated singularity)이 만날 때는 주로 지표(index) 혹은 회전 지표(rotation index) $I_c(\bar p)$로 이름 붙인다. 왜냐하면 권선수는 단순한 양이지만 곡선이나 표면의 전체적인 성질을 나타내는 중요한 숫자라서, 밋밋한 권선수보다 형태를 분류하는 지표란 어감이 더 좋기 때문이다. 여기서 지표는 권선수의 일종이므로 정수이며, [그림 3]에 나온 고립된 특이점은 닫힌 곡선 $c$를 아무리 줄여도 지표가 0이 될 수 없는 곡선의 내부점이다.
 (3)
(3)여기서 $\bar p$는 고립된 특이점 혹은 일반점이다. 연속 벡터 함수(continuous vector function)의 지표는 복소 함수(complex function)와 비슷한 성질을 가지고 있다.
[연속 벡터 함수의 지표(index of continuous vector function) 성질] [4]
단순 닫힌 곡선(simple closed curve) $c$상에서 연속 벡터 함수가 비소멸(nonvanishing)혹은 언제나 0이 아닐 경우는 다음 성질이 성립한다.
(a) 일반점: $I_c(\bar p)$ = $0$
(b) 안장점(saddle or saddle point): $I_c(\bar p)$ = $-n$, $n$은 양수
(c) 안장점이 아닌 영점(zero): $I_c(\bar p)$ = $+n$, $n$은 양수
(d) 닫힌 곡선의 변형: $I_c(\bar p)$ = $I_{c'}(\bar p)$
(e) 닫힌 곡선의 분해 혹은 병합: $I_{c_1 + c_2}(\bar p)$ = $I_{c_1} (\bar p)+ I_{c_2}(\bar p)$(f) 여러 고정점(fixed point): $I_c(\bar p_1, \bar p_2)$ = $I_c(\bar p_1)$ + $I_c(\bar p_2)$, $\bar p_1, \bar p_2$는 고정점
(g) 모든 고정점을 포함하는 궤적(trajectory): $I_c(\bar p)$ = $\sum_{k=1}^m I_c (\bar p_k)$ = $+1$
일반점 $\bar p$를 내부에 두고 일주하는 닫힌 경로 $c$에서는 편각 $\phi_c$가 한 바퀴 이상을 완전히 돌지 못하여서 권선수는 항상 0이 된다. 여기서 경로상의 벡터 함수는 비소멸이라서 편각이 정확히 정의된다.
혹은 명제 (d)를 쓰면 더 쉽게 증명된다. 곡선 $c$ 안에는 고정점이 없어서 더 작은 곡선 $c'$으로 줄여도 지표가 유지된다. 이를 한없이 반복한 경우, 줄어든 곡선은 거의 $\bar p$만 회전한다. 이 점은 상수처럼 보여서 편각이 바뀌지 않으므로 지표는 항상 0으로 나온다.
[명제 (b)의 증명]
[그림 3]에 나온 빨간색 안장점을 포함하는 닫힌 곡선을 새로 정해서 벡터의 회전 각도를 모두 더하면 항상 $-2 \pi$가 된다. 일반적으로 이러한 회전은 여러 바퀴가 될 수 있으므로 지표는 $-n$으로 표현된다. 여기서 $n$은 0이 아닌 양수이다. 벡터 함수의 안장점(saddle or saddle point)은 방향에 따라 인력(attraction)과 척력(repulsion)이 동시에 존재하는 불안정점(unstable point)이다. [그림 3]의 빨간색 안장점 주변을 보면, 45˚와 -135˚ 방향에서는 벡터가 안장점으로 모이며[인력] 135˚와 -45˚에서는 안장점 바깥으로 벡터가 나간다[척력]. 더 구체적으로 안장점 근방의 벡터 분포를 인력이 작용하는 방향은 ∪로, 척력 방향으로는 ∩로 간주하면, 안장점 근방은 말 안장과 비슷한 모양이며 안장점에서 조금만 벗어나도 굴러떨어진다. 안장점의 대표적 예는 쌍곡선(hyperbola)스러운 $f(x, y)$ = $x^2 - y^2$이다. 이 스칼라 함수에 구배(gradient)를 취하면 벡터 함수는 $\bar \nabla f$ = $2x \hat x - 2y \hat y$로 나온다. 그러면 안장점 $(0, 0)$에서 힘은 0이 되지만 안장점을 벗어나면 방향에 따라 인력과 척력이 동시에 발생한다. 이러한 안장점은 벡터 함수의 영점(zero)이며 고정점(fixed point)이다. 벡터 함수의 영점은 벡터 크기가 0이 되는 점이다. 비슷하게 벡터 함수의 고정점은 벡터가 사라져서(vanishing) 어느 방향으로도 움직일 수 없는 점이다. 그래서 움직임이 없는 고정점은 크기가 0인 영점과 실질적으로 같다. 반대로 고정점이 아닌 일반점은 보통 비고정점(non-fixed point)으로 부른다.


[그림 4] 양전하 ($+$)와 음전하 ($-$)의 전기력선(출처: wikipedia.org)
[명제 (c)의 증명]
명제 (b)의 증명처럼 초록색 중심점을 내부에 담도록 닫힌 곡선을 만들어서 권선수를 재면 항상 0보다 큰 $+n$이 나온다. 여기서 중심점(center or center point)은 주변 벡터가 [그림 3]처럼 회전하는 점이다. 안장점이 아닌 영점은 [그림 3]의 초록색 중심점이나 [그림 4]와 같을 수 있다. 어느 경우든지 기준 단위 벡터 $\hat e_r$을 정해놓고 벡터가 돌아가는 각도를 추적한다. 그러면 신기하게도 벡터가 어느 방향으로 회전하든지 혹은 벡터의 원천(source)이나 수채(sink)가 되든지, 모든 영점의 지표는 언제나 $+1$이다. 이런 영점에 [그림 4]의 음전하와 같은 인력이 작용하면 안장점이 아닌 영점은 안정점(stable point)이다. 반면에 양전하의 전기력선처럼 척력이 있는 경우는 불안정점(unstable point)이 된다. 안장점이 아닌 원점의 예시는 원(circle) 방정식인 $f(x, y)$ = $x^2 + y^2$으로 만들 수 있다. 이 함수에 구배를 적용한 벡터 함수는 $\bar \nabla f$ = $2x \hat x + 2y \hat y$이다. 이때 $\bar \nabla f$의 영점은 $(0, 0)$이며 벡터의 원천 역할을 한다.
[명제 (d)의 증명]
고정점을 내부에 두면서 변형한 닫힌 곡선 $c'$의 지표를 $I_{c'}(\bar p)$로 둔다. 그러면 우리가 고려하는 연속 벡터 함수의 지표는 끊어지지 않고 $I_{c}(\bar p)$에서 $I_{c'}(\bar p)$로 바뀐다. 하지만 지표는 권선수이므로 정수만 될 수 있다. 연속인 정수 함수는 상수 함수만 가능하므로 곡선을 수정해도 지표는 그대로이다.

[그림 5] 변형을 통한 닫힌 곡선의 분해와 병합
[명제 (e)의 증명]
[그림 5]에 그린 단순 닫힌 곡선 $c$를 또 다른 닫힌 곡선 $c_1, c_2$로 분해할 때는 복소 함수론의 경로 적분(contour integral)에서 유추한 방식을 쓴다. 먼저 명제 (d)를 써서 $c$의 왼쪽과 오른쪽 경로를 조금씩 내부로 넣는다. 이 과정을 지속해서 내부에 들어간 경로가 서로 만나도록 함으로써 $c_1, c_2$로 닫힌 곡선이 나누어지도록 한다. 이때 바뀐 경로에도 고정점이 없어야 한다. 따라서 고정점을 피해 닫힌 곡선 $c$를 [그림 5]처럼 변형해도 지표는 바뀌지 않으며, 닫힌 곡선 $c_1, c_2$의 지표는 $I_{c_1}(\bar p)$와 $I_{c_2}(\bar p)$의 합으로 계산할 수 있다.

[그림 6] 극점(pole)을 피하는 경로 적분의 변형
[명제 (f)의 증명]
명제 (e)의 증명처럼 복소 함수론에서 실마리를 찾아서 [그림 6]처럼 고정점을 둘러싸는 경로를 가지도록 닫힌 곡선을 변형한다. 그러면 명제 (e)로 인해 각 고정점을 둘러싸는 닫힌 경로의 지표 합으로 전체 지표 $I_c(\bar p_1, \bar p_2)$가 결정된다.

[그림 7] 구면에 형성된 벡터 함수의 궤적: 영점 혹은 고정점이 하나(출처: wikipedia.org)
[명제 (g)의 증명]
연속 벡터 함수(continuous vector function)의 궤적(trajectory)은 [그림 7]과 같이 특정 위치의 벡터가 향하는 방향을 따라 연속적으로 연결한 곡선이다. 이런 궤적을 이해한 상태에서 [그림 3]을 보면 궤적의 특징이 명확히 보인다. 바로 등고선처럼 연결한 선이 [그림 3]에 나오는 벡터 함수의 궤적이다. 이 궤적을 따라가는 단순 닫힌 곡선의 벡터 편각을 모두 추적하면 [그림 3]이든 [그림 7]이든 항상 $2 \pi$이기 때문에, 모든 궤적의 지표는 언제나 $+1$로 나온다. 또한 명제 (f)의 결과에 의해 궤적의 지표는 내부에 있는 여러 고정점으로 분리되어 계산될 수 있다. 예시적으로 [그림 3]을 다시 본다. 초록색 중심점 $\bar p_1, \bar p_2$의 지표는 각각 $I_c(\bar p_1)$ = $I_c(\bar p_2)$ = $1$이고, 빨간색 안장점 $\bar p_3$가 만드는 지표는 $-1$이다. 이를 모두 더하면 $1+1-1$ = $1$이 되므로, 모든 궤적의 지표는 항상 $1$이라는 명제 (g)의 정확성을 재확인할 수 있다.
______________________________
이제 닫힌 곡선의 지표 이론(index theory)이 우리 사고의 범주에 있기 때문에 더 심오한 정리인 털공 정리(hairy ball theorem, HBT)로 나갈 수 있다. [그림 1]의 소개처럼 털공의 털을 모든 영역에서 가지런하게 빗을 수는 없다는 일상적인 관찰을 수학으로 증명한 정리라서 편하게 털공 정리로 부른다.
[털공 정리(hairy ball theorem, HBT)] [2], [3]
구면(spherical surface)에 접한 벡터 함수(tangent vector function)는 반드시 한 곳 이상에서 영점이 생긴다.
[증명]
[그림 7]과 같은 임의의 벡터 함수를 고려한다. 이 벡터 함수는 구의 표면에 접해있는 접선 벡터(tangent vector)의 모임이다. 먼저 이 벡터 함수의 영점은 없다고 가정한다. 이를 활용해서 [그림 7]에 나온 임의의 벡터 하나를 뽑는다. 언제나 영점이 없기 때문에 이 벡터는 방향이 딱 하나로 결정된다. 또한 벡터 함수는 연속이라서 끊기지 않고 이 방향을 계속 따라갈 수 있다. 계속 진행하면 원래 출발한 벡터와 만나서, 이 벡터의 경로는 궤적을 이룬다. 그러면 지표 성질의 명제 (g)에 따라 우리가 편성한 궤적의 지표는 1로 나온다. 지표가 1인 상태에서 지표 성질의 명제 (d)를 이용함으로써 궤적의 둘레 길이를 계속 줄일 수 있다. 왜냐하면 영점이 없기 때문에 닫힌 곡선의 변형은 자유롭기 때문이다. 궤적이 지속적으로 축소되면 결국 한 점에 이를 것이다. 지표가 1이며 한 점을 따라 도는 궤적은 [그림 3]에 보인 중심점 주변부이기 때문에 영점이 반드시 생긴다. 결국 영점이 없다는 전제가 잘못이라서, 구면에 만든 접선 벡터의 연속된 집합은 한 곳 이상에서 영점이 꼭 생겨야 한다.
______________________________
털공 정리 관점으로 [그림 1, 7]을 관찰한다. 구 좌표계(spherical coordinate system)처럼 [그림 1]은 극축(pole axis)에서 영점이 2개 생긴다. 하지만 영점이 반드시 2개일 필요는 없다. [그림 7]과 같이 [그림 1]의 두 영점이 한 점으로 모일 수도 있다. 이 경우 영점은 달랑 1개이다. 그러나 표면에 지표가 1인 영점이 2개 혹은 지표 1인 영점이 모여서 하나가 생기더라도, 연속 벡터 함수가 생성하는 구면의 지표는 항상 $1+1$ = $2$로 정해진다.

[그림 8] 다이폴 안테나(dipole antenna)로 만든 전방향 복사 패턴(omnidirectional radiation pattern)(출처: wikipedia.org)
이제는 모든 방향으로 전자파를 복사하는 전방향 안테나의 불가능성을 증명할 차례이다. [그림 8]처럼 다이폴 안테나(dipole antenna)를 아무리 작게 만들어도 방위각 $\phi$방향으로만 골고루 복사가 되는 전방향 안테나(omnidirectional antenna)만 설계 가능하다. 여분의 각도인 극고도각 $\theta$ 방향에서는 전자파가 나가지 않는 영점 혹은 공점(null)이 존재한다. 털공 정리는 우리가 온갖 노력을 다해도 등방성 안테나를 만들 수 없다고 말한다.
[등방성 안테나의 불가능성(impossibility of isotropic antenna)] [1]
모든 각도로 골고루 복사되는 등방성 안테나는 구현할 수 없다.
[증명: 털공 정리]
안테나를 둘러싸는 구면을 하나 가정한다. 털공 정리에 의해 이 구면상에는 접선 전기장이나 자기장이 0인 지점이 하나 이상 생긴다. 우리는 가상 구면의 반지름을 마음대로 계속 늘릴 수 있기 때문에, 안테나에서 한없이 멀어지더라도 접선 전자기장이 0인 각도는 꼭 생긴다.
[증명: 헬름홀츠의 정리]
안테나 외부에 복사장이 존재하는 구면을 하나 잡는다. 구면 내부의 전자기장은 표면 등가의 원리(surface equivalence principle)를 준용해서 0으로 만든다. 이 구면에 벡터의 영점이 없다는 말은 [그림 3, 4]와 같은 접선 벡터 모양이 생기지 않는다는 뜻이다. 발산(divergence)과 회전(curl) 연산자 관점에서 [그림 3, 4]의 영점은 각각 회전 및 발산 원천에 해당하므로, 복사 전기장 $\bar E$에 대해 발산과 회전 원천이 없는 $\bar \nabla \times \bar E$ = $0$, $\bar \nabla \cdot \bar E$ = $0$을 도출한다. 그러면 헬름홀츠의 정리(Helmholtz' theorem)에 의해 이 전기장은 상수 벡터 $\bar E$ = $\bar E_0$만 가능하다. 상수 전기장 $\bar E_0$은 전자기파를 만들 수 없기 때문에, 구면 어딘가에 벡터의 발산이나 회전 원천이 반드시 있어야 한다. 이런 원천은 당연히 그 지점에서 [그림 3, 4]처럼 생긴 영점을 만든다.
______________________________
등방성 안테나는 현실에서 구현할 수 없기 때문에 우리가 연구할 때는 최대한 등방성 안테나에 가깝게 만드는 준등방성 안테나(quasi-isotropic antenna)를 지향한다[5], [6].
[참고문헌]
[1] H. F. Mathis, "A short proof that an isotropic antenna is impossible," Proc. IRE, vol. 39, no. 8, p. 970, Aug. 1951.
[2] P. McGrath, "An extremely short proof of the hairy ball theorem," Amer. Math. Monthly, vol. 123, no. 5, pp. 502–503, May 2016.
[3] E. Curtin, "Another short proof of the hairy ball theorem," Amer. Math. Monthly, vol. 125, no. 5, pp. 462–463, May 2018.
[4] S. H. Strogatz, Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, Reading, MA, USA: Perseus Books, 1994.
[5] J.-H. Kim and S. Nam, "A compact quasi-isotropic antenna based on folded split-ring resonators," IEEE Antennas Wirel. Propag. Lett., vol. 16, pp. 294–297, 2017.
[6] S. I. Hussain Shah, S. M. Radha, P. Park, and I.-J. Yoon, "Recent advancements in quasi-isotropic antennas: A review," IEEE Access, vol. 9, pp. 146296–146317, 2021.

 (1)
(1) (2)
(2) (3a)
(3a) (3b)
(3b) (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) (2.1)
(2.1) (2.2)
(2.2)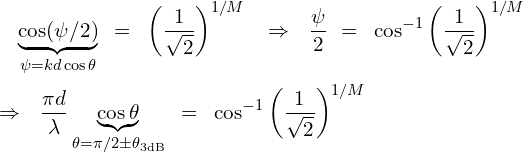 (2.4a)
(2.4a) (2.4b)
(2.4b) (2.4c)
(2.4c) (2.5a)
(2.5a) (2.5b)
(2.5b) (2.5c)
(2.5c) (2.6a)
(2.6a) (2.6b: $d$ = $\lambda/2$)
(2.6b: $d$ = $\lambda/2$) (2.6c)
(2.6c) (3.1)
(3.1)
 (3.2a)
(3.2a) (3.2b)
(3.2b) (3.3a)
(3.3a) (3.3b)
(3.3b) (3.4)
(3.4)

 (3.5b)
(3.5b)
 (3.7a)
(3.7a) (3.7b)
(3.7b) (3.7c)
(3.7c) (3.8a)
(3.8a) (3.8b)
(3.8b) (3.8c)
(3.8c) (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5)