[경고] 아래 글을 읽지 않고 "정전장과 정자장"을 보면 바보로 느껴질 수 있습니다.

(a) 커패시터에 생기는 전기장

(b) 인덕터에 생기는 자기장
[그림 1] 정전장과 정자장의 예시(출처: wikipedia.org)
전기장(electric field)과 자기장(magnetic field)의 시간 변화가 없는 경우는 정전장(靜電場, electrostatics or static electric field)[7]과 정자장(靜磁場, magnetostatics or static magnetic field)으로 이름 붙인다. 정전장과 정자장은 모두 정역학(靜力學, statics)에 속하며, 이 두 장을 합쳐서 정적장(靜的場, static field)으로 부른다. 이때 시간 미분은 $\partial / \partial t$ = $0$이 되기 때문에, 맥스웰 방정식(Maxwell's equations)에서 전기장 $\bar E$와 자기장 $\bar H$는 완전히 분리되고 전자기파(electromagnetic wave)는 발생하지 않는다.
 (1: 정전장)
(1: 정전장) (2: 정자장)
(2: 정자장)여기서 $\bar D$ = $\epsilon \bar E$, $\bar B$ = $\mu \bar H$, $\bar \nabla \cdot \bar J$ = $0$이다. 따라서 전기장은 정전장으로, 자기장은 정자장으로 간략화하며 이 둘을 따로 해석할 수 있다. 회로 이론(circuit theory) 관점에서 정전장과 정자장은 직류(直流, direct current, DC) 조건이며, 직류 회로 이론(DC circuit theory)의 근원이 된다.
도선을 구성하는 물질의 전기 전도도(electrical conductivity) $\sigma$가 유한한 경우는 정전장과 정자장이 옴의 법칙(Ohm's law)으로 서로 연결된다.
 (3: 정전장과 정자장)
(3: 정전장과 정자장)여기서 $\bar J$ = $\sigma \bar E$이다. 다만 $\sigma$를 사용할 때는 맥스웰 방정식에 어긋나지 않도록 $\bar J$와 $\bar E$의 조건을 면밀히 따져야 한다. 만약 $\sigma$가 무한대로 가면, 전류 밀도 $\bar J$가 발산하지 않도록 전기장은 $\bar E$ = $0$이 되어야 한다. 식 (1)로 인해 전하 밀도도 $\rho$ = $\bar \nabla \cdot (\epsilon \bar E)$ = $0$이다. 전기 전도도를 유한하게 제한한 경우는 매질 내부에 전기장이 존재할 수 있다. 하지만 전류 밀도의 발산은 0이기 때문에 $\bar \nabla \cdot \bar J$ = $\sigma/\epsilon (\bar \nabla \cdot \bar D)$ = $\sigma/\epsilon \cdot \rho$ = $0$이다. 즉, 매질에 전기 전도도가 조금이라도 있으면, 매질 내부에 남아있는 전하 밀도 $\rho$는 항상 0이다. 이는 시간에 대해 불변인 정전장 조건에 기인한다. 전하가 움직이는 상태는 정전장이 아니며, 전하가 다 움직여서 정지한 때가 바로 정전장의 조건이다. 하지만 전하가 이미 다 움직였다면 매질 내부에는 전하가 남아있지 않아서, 앞선 결과처럼 매질 내부에는 어떠한 전하도 없다.
정전장과 정자장은 시간 변화가 없고 서로 독립이라는 개념은 전자파에서 주파수를 0으로 만드는 조건과 분명하게 구별된다. 왜냐하면 전자파는 전기장과 자기장의 비율인 파동 임피던스(wave impedance) $\eta$가 요구하는 관계가 있기 때문에, 주파수를 낮추더라도 전기장과 자기장은 $\eta$ 비율을 항상 충족한다. 하지만 정전장과 정자장은 독립된 특성이므로, 정전장과 정자장은 어떤 관련도 가질 필요가 없다.
1. 정전장(electrostatics or static electric field)
정전장은 벡터장(vector field)이라 다루기 어려워서 전압(voltage), 전기 스칼라 포텐셜(electric scalar potential), 혹은 정전 포텐셜(voltage or electrostatic potential) $\phi$를 도입해서 스칼라(scalar)로 처리한다.
 (1.1: 푸아송 방정식)
(1.1: 푸아송 방정식)
[그림 1.1] 개구면(aperture)을 통한 전기장의 침투(그림 출처: [2])
복잡한 전기장의 변화를 단순한 정전장으로 어림잡는 정전 근사(electrostatic approximation)는 전자기 간섭(electromagnetic interference, EMI)의 분석에 많이 사용된다. [그림 1.1]처럼 복사원에서 방출한 전기장이 금속 막(metallic screen)에 뚫린 개구면(aperture)으로 침투(penetration)하는 환경을 가정한다. 개구면이 뚫린 면의 법선 벡터는 $\hat z$이다. 이 현상을 공식화하기 위해 $z$방향으로 전기장만 있는 TM${}^z$ 모드(transverse magnetic mode for the $z$-axis)[$E_z \ne 0$, $H_z$ = $0$]를 가정하고 MNL 벡터 파동 함수(vector wave functions)를 도입한다.
 (1.1)
(1.1)여기서 $\bar e_n^E(\bar r)$ = $\bar N^E$ = $1/k_0 \cdot \bar \nabla \times \bar M^E$, $\bar h_n^E(\bar r)$ = $\bar M^E$ = $1/k_0 \cdot \bar \nabla \times \bar N^E$; $\bar e_n^E(\bar r)$과 $\bar h_n^E(\bar r)$는 개구면에 존재하는 $n$번 모드 함수(mode function), 위첨자 $E$는 전기장 경계 조건과 $z$방향으로 TM 모드를 의미, $E_n, H_n$은 각각 전자기장의 $n$번 모드 계수(modal coefficient), $k_0$은 자유 공간(free space)의 파수(wavenumber)이다. 물리학자 베테Hans Bethe(1906–2005)가 제안한 작은 구멍에 의한 회절 이론(theory of diffraction by small holes)[1]을 시작점으로 금속 막을 넘어 침투하는 전기장의 결합 계수 $C_n^E(z)$를 정의한다[3]. 금속 막에서 표면에 존재하는 접선 전기장은 0이 되어야 하므로, 아래 결합 계수 정의는 개구면에서만 정의되어서 유용하다.
 (1.2)
(1.2)여기서 $s$는 개구면의 면적, $d \bar a$ = $da \hat n$, $\hat n$ = $\hat z$; 결합 계수를 만들 때 포인팅의 정리(Poynting's theorem)를 써서 $z$방향 전력을 만들 수 있는 전기장만 고려하며, 개구면의 둘레에서 접선 전기장은 0이다. 개구면이 파장에 비해 작다고 생각해서 자기장의 모드 함수 $\bar h_n^E(\bar r)$을 다변수 테일러 급수(multivariate Taylor series)로 근사한다.
 (1.3)
(1.3)여기서 $z$ = $0$에 개구면 끝단이 위치하고 이 개구면의 기준점은 $\bar r$ = $\bar 0$이다. 식 (1.3)을 식 (1.2)에 대입함으로써 $z$ = $0$에서 $C_n^E(z)$의 근사식을 얻는다.
 (1.4a)
(1.4a) (1.4b)
(1.4b) (1.4c)
(1.4c)식 (1.4)에 정전 근사인 $\bar E$ $\approx$ $- \bar \nabla \phi$를 적용해 정리한다.[정확하게는 $-\partial \bar A / \partial t$가 추가로 필요하다.]
 (1.5a)
(1.5a) (1.5b)
(1.5b) (1.5c)
(1.5c) (1.5d)
(1.5d)여기서 $\partial_x h_{n,y}^E(\bar 0) - \partial_y h_{n,x}^E(\bar 0)$ = $k_0 e_{n,z}^E(\bar 0)$; $c$는 개구면 면적 $s$의 둘레를 따라 돈다. 최종적으로 TM${}^z$ 모드의 결합 계수 $C_n^E(0)$는 $E_z$ 전기장에 영향을 받고 [그림 1.1]처럼 전기 쌍극자 모멘트(electric dipole moment)에 의한 전기장과 비슷한 모양을 만든다. 따라서 투과 전기장 $\bar E_t$를 분극도(polarization) $\bar P$로 어림잡아서 전기 감수율(electric susceptibility) $\chi_e(z)$와 함께 표현한다.
식 (1.5d)와 (1.6a)를 활용해서 평균 전기 감수율(mean electric susceptibility) $\langle \chi_e(z) \rangle$를 최대한 간단하게 공식화한다[4].
 (1.6b)
(1.6b)여기서 $C_n^E(z)$ $\propto$ $\int_s \phi\,dxdy$ $\propto$ $E_{t,z}(\bar r)$; $A$는 개구면의 면적, 단위를 맞추기 위해 입사 전기장 $\bar E_i$ 대신 입사 정전 포텐셜 $\phi_i$를 사용한다.
평균 전기 감수율의 유도가 약간 엉성하다고 생각할 수 있다. 하지만 개구면의 모양과 금속 막의 두께 영향을 상대적으로 비교하기 위한 기법이라서 난처함은 없다. 우리가 이론을 일관되게 적용하고 있으며 DC에서 실험하기가 좋기 때문에 식 (1.6b)는 나무랄 곳이 없는 결과물이다. 또한 전자파의 투과를 다룰 때 DC인 정전 근사를 쓰는 방식은 문제가 있다고 생각할지도 모른다. 그러나 전송선 이론(transmission line theory)에서 정적 근사(static approximation)를 써서 단위 길이당 유도 용량(inductance, L)과 전기 용량(capacitance, C)을 구하는 방식을 기억해야 한다. DC에서 구한 $L, C$이지만 전압파와 전류파를 다루는 전송선에 충분히 쓸 수 있다. 마찬가지로 정전 근사로 유도한 식 (1.6b)는 분명한 근사이지만, 혼란스러운 전자파 침투를 분석하는 훌륭한 기준이 된다.

[그림 1.2] 무한히 긴 도선을 흐르는 전류(출처: wikipedia.org)
[그림 1.2]의 구조처럼 무한히 긴 도선을 흐르는 전류 $I$는 옴의 법칙에 따라 도선 내부에 $E_0$ = $J / \sigma$ = $I \mathbin{/} (\sigma A)$인 전기장을 만든다. 하지만 무한히 긴 도선이라서 도선 내부에 전하가 쌓일 공간은 없어서 전하 밀도는 항상 0다. [그림 1.2]의 정전장 해는 다음과 같다.
 (1.7)
(1.7)여기서 $a$와 $A$는 각각 도선의 반지름과 단면적, 전류는 $z$방향으로 흐른다. 식 (1.7)에 가우스 정리(Gauss' theorem)를 쓰면 $\oint_s \bar E \cdot d \bar a$ = $0$이 되기 때문에, 도선의 모든 영역에서 전하는 없다.

[그림 1.3] 직류 회로에 발생하는 전기장 분포(출처: wikipedia.org)
하지만 [그림 1.3]처럼 도선이 유한해서 휘어지면 [그림 1.2]에서는 없던 표면 전하 밀도(surface charge density) $\rho_s$가 출현한다. 왜냐하면 도선은 전기 전도도가 무한대라서 전기장은 없고 저항 내부에는 식 (1.7)과 같은 전기장 $E_0$이 있는 전기장의 불균일성이 생기기 때문이다. 이 경우 발생하는 표면 전하 밀도는 $\rho_s$ = $Q/A$ = $E_0 - 0$이다. 간단한 막대형 저항인 경우는 $\rho_s$가 $V$ = $IR$로 쉽게 연결된다.
 (1.8)
(1.8)여기서 $l$은 저항의 길이이다. 또한 전류가 저항 내부를 균일하게 흘러서 전류 밀도가 일정하고 전기장의 변동도 없으면, 저항 내부에는 전하가 만들어지지 않는다. 대신 도선과 저항이 만나는 지점에만 표면 전하 밀도가 나타난다. 다른 관점으로 저항이 복잡한 모양과 다른 전기 전도도를 가지면 직류 회로의 전하 분포는 [그림 1.3]보다 더욱 복잡하게 발생한다[6]. 식 (3)의 맥스웰 방정식을 풀어서 전하 분포를 계산할 수도 있지만, 저항의 직렬과 병렬 근사를 활용할 여지도 존재한다.
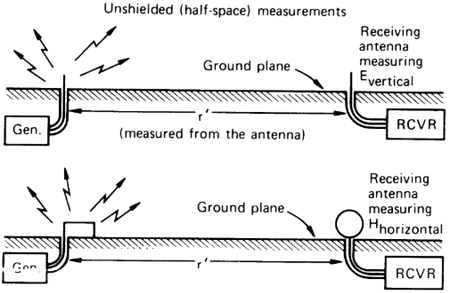
(a) 차폐가 없는 측정

(b) 차폐가 있는 측정
[그림 1.4] 차폐 효과의 측정을 위한 설정(출처: [8])
정전장에서 시작해서 저주파 전기장에 의한 개구면 침투(aperture penetration)를 정량화하는 지표로 전기 차폐 효과(electric shielding effectiveness)를 많이 쓴다[8].
 (1.9)
(1.9)여기서 $E_i$와 $P_i$는 각각 입사한 전기장 및 전력, $E_t$와 $P_t$는 침투 혹은 투과에 해당하는 양이다. 전자기 간섭(electromagnetic interference, EMI)을 막는 수준을 계량화한 차폐 효과(shielding effectiveness, SE)의 측정은 [그림 1.4]를 따른다. 차폐가 없는 조건에서 입사 전기장 $E_i$나 입사 전력 $P_i$를 잰다. 그 다음에 차폐 함체를 피시험 장치(device under test, DUT)에 씌우고 침투하거나 투과한 전기장 $E_t$나 $P_t$를 얻은 후 식 (1.9)에 따라 데시벨(decibel)로 표현한다. 차폐 효과가 클수록 SE는 커지며, 차폐 효과가 없으면 SE는 0 dB가 된다. 요즘은 EMI보다 전자기 펄스(electromagnetic pulse, EMP)의 방호(protection) 때문에 SE 개념을 전자파 차폐 시설의 분석에 활용한다[9]. EMP를 방호하는 차폐실의 SE는 보통 80 dB 정도이다.
2. 정자장(magnetostatics or static magnetic field)

[그림 2.1] 두 개의 자석이 만드는 자기 쌍극자의 자기장(출처: wikipedia.org)
정전 포텐셜 $\phi$에 대응하는 개념으로 자기장 $\bar H$를 위한 자기 스칼라 포텐셜(magnetic scalar potential) 혹은 정자 포텐셜(magnetostatic potential) $\psi$가 존재한다. 선 적분 $c$의 내부에 전류가 없다면, 자기장은 정자 포텐셜의 구배(gradient)로 정의될 수 있다.
 (2.1)
(2.1)여기서 $\oint_c \bar H \cdot d \bar l$ = $0$이다. 식 (1.1)처럼 자기장의 푸아송 방정식도 만든다.
 (2.2)
(2.2)여기서 $\bar \nabla \cdot \bar B$ = $0$; $\rho_m$은 자하 밀도(magnetic charge density), 전하처럼 자하(magnetic charge)에 의해 자기장이 생긴다고 생각해서 $\bar \nabla \cdot (\mu_0 \bar H)$ = $\rho_m$으로 설정한다.

[그림 2.2] 동축선의 단면 구조(그림 출처: wikipedia.org)
자기장의 선 적분 내부에 전류가 없는 경우는 정전 포텐셜과 정자 포텐셜의 특성은 같다. 그러나 내부에 전류가 생기면 정자 포텐셜은 보존적이지 않아서 선 적분의 회전 회수에 따라 값이 달라진다[5]. 예를 들어, [그림 2.2]와 같은 동축선의 자기장을 관찰한다. 암페어 주회 적분 법칙(Ampere's circuital law)으로 자기장 $\bar H$를 구한 후, $\phi$에 대해 적분해서 $\psi$를 결정한다.
 (2.3)
(2.3)
[그림 2.2] 금속 막에 만들어진 2개의 개구면(그림 출처: [5])
정자 포텐셜의 일가성을 형성하는 가지 자름은 3차원 구조에도 필요하다[5]. [그림 2.2]에 나온 2개의 개구면을 통과하는 빨간색 폐경로 $c$ 내부에는 금속이 있어서, 이 경로 안에 전류가 있을 수 있다. 이때는 식 (2.3)처럼 다가성이 생기기 때문에, 문제를 풀 때 중첩 원리(superposition principle)로 도출하는 두 영역에 가지 상수 $B_0, B_1$을 각각 도입한다. 가지 상수 $B_0, B_1$은 두 영역의 어떤 경계면에서 $B_1 - B_0$인 불연속성을 만들지만, $\psi$는 일가성을 가지도록 도운다.

 (2.4)
(2.4)

[그림 2.3] 개구면(aperture)을 통한 자기장의 침투(그림 출처: [2])
접선 전기장이 개구면을 제외한 금속 막에서 0이 되는 경계 조건을 활용하기 위해, $z$방향으로 전기장이 없는 TE${}^z$ 모드[$H_z \ne 0$, $E_z$ = $0$]에 대해 식 (1.2)와 유사한 결합 계수 $C_n^H(z)$를 정의한다.
 (2.4)
(2.4)여기서 $\bar e_n^H(\bar r)$ = $\bar M^H$ = $1/k_0 \cdot \bar \nabla \times \bar N^H$, $\bar h_n^H(\bar r)$ = $\bar N^H$ = $1/k_0 \cdot \bar \nabla \times \bar M^H$이다. 식 (1.4)와 (1.5)를 TE${}^z$ 모드에 적용하면, 개구면의 끝인 $z$ = $0$에서 식 (2.4)가 간략화된다[3].
 (2.5a)
(2.5a) (2.5b)
(2.5b)여기서 $z$방향 전기장이 없어서 $P_n^H$ = $0$, $H_z$는 TE${}^z$ 모드의 $z$방향 자기장이다. 식 (2.5b)는 물리적 설명이 추가로 필요하다. 자기장 $H_z$가 개구면으로 입사한 경우, 투과된 자기장은 [그림 2.3]처럼 생기며 그 벡터 방향은 $x, y$축이 된다. 그래서 투과 자기장 $\bar H_t$는 금속 막에 평행한 $x, y$방향을 모두 고려해야 한다. 이 특성은 자화도(magnetization) $\bar M$을 잣대로 벡터량인 자기 감수율(magnetic susceptibility) $\bar \chi_m (z)$로 근사된다.
 (2.6a)
(2.6a)식 (2.5b)에 나온 $H_z$에 정자장을 쓰는 정자 근사(magnetostatic approximation)를 써서 $H_z$ = $-\partial \psi / \partial z$로 둔다.[포텐셜 이론을 쓰면 $\bar H$ = $-\partial \bar F/\partial t - \bar \nabla \psi$이다.] 그러면 식 (1.6b)처럼 $x,y$방향에 대한 평균 자기 감수율 $\langle \chi_{mx}(z) \rangle$과 $\langle \chi_{my}(z) \rangle$가 각각 정의된다.
 (2.6b)
(2.6b)여기서 $\psi_i$는 입사 정자 포텐셜이다. 정자 포텐셜과 자기장의 관계성을 명확히 하기 위해 식 (2.6b)에 부호 ($-$)를 붙이기도 한다.
식 (1.9)와 동일한 방식으로 저주파 자기장에 대한 자기 차폐 효과(magnetic shielding effectiveness)를 정의한다.
 (2.7)
(2.7)여기서 $H_i$와 $H_t$는 각각 입사 자기장과 차폐를 뚫고 침투한 자기장이다.
[참고문헌]
[1] H. A. Bethe, "Theory of diffraction by small holes," Phys. Rev., vol. 66, no. 7–8, pp. 163–182, Oct. 1944.
[2] F. de Meulenaere and J. van Bladel, "Polarizability of some small apertures," IEEE Trans. Antennas Propag., vol. 25, no. 2, pp. 198–205, Mar. 1977.
[3] R. L. Gluckstern, R. Li, and R. K. Cooper, "Electric polarizability and magnetic susceptibility of small holes in a thin screen," IEEE Trans. Microw. Theory Tech., vol. 38, no. 2, pp. 186–192, Feb. 1990.
[4] J. H. Lee and H. J. Eom, "Electrostatic potential through a circular aperture in a thick conducting plane," IEEE Trans. Microw. Theory Tech., vol. 44, no. 2, pp. 341–343, Feb. 1996.
[5] H. J. Eom, J. W. Zeong, J. S. Seo, and J. G. Lee, "Magnetostatic potential penetration into two circular apertures in a thick conducting plane," IEEE Trans. Electromagn. Compat., vol. 43, no. 3, pp. 399–402, Aug. 2001.
[6] 유태훈, "전기 회로에서 저항성 도체의 표면전하 분포와 정상전류 및 에너지 흐름", 전자공학회논문지, 제59권, 제9호, pp. 111–120, 2022년 9월.
[7] F. Olyslager and I. V. Lindell, "Closed form solutions of Maxwell's equations in the computer age," URSI Radio Sci. Bull., vol. 2003, no. 305, pp. 30–37, Jun. 2003.
[8] H. A. Méndez, "Shielding theory of enclosures with apertures," IEEE Trans. Electromagn. Compat., vol. 20, no. 2, pp. 296–305, May 1978.
[9] 박현호, 형창희, 권종화, "직사각형 루프 안테나를 이용한 차폐실의 자기장 차폐효과 측정 방법 개선", 한국전자파학회논문지, 제30권, 제4호, pp. 320–323, 2019년 4월.
댓글 없음 :
댓글 쓰기
욕설이나 스팸글은 삭제될 수 있습니다. [전파거북이]는 선플운동의 아름다운 인터넷을 지지합니다.