균일 평면파의 의미(Uniform Plane Wave)

[경고] 아래 글을 읽지 않고 "균일 평면파"를 보면 바보로 느껴질 수 있습니다. 
1. 맥스웰 방정식
2. 전자기장 파동 방정식
3. 페이저를 이용한 맥스웰 방정식

[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.

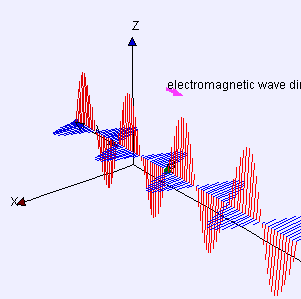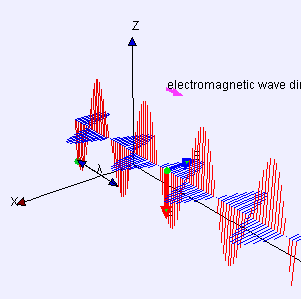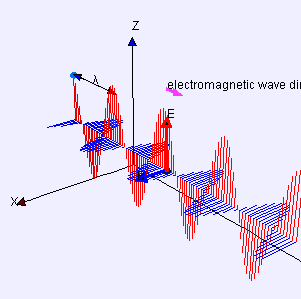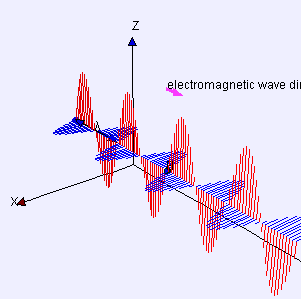
초등 전자기학을 배울 때 처음 만나는 전자파 공식은 [그림 1, 2]에 있는 균일 평면파(uniform plane wave)이다. 균일 평면파는 물리적으로는 말이 안되지만 파면(波面, wavefront: 파동 함수가 동일한 값을 가진 면)이 평면(平面, plane)이기 때문에 쉬워서 가장 처음 배우게 된다. 파면이 평면이라는 뜻은 해당 평면에서 전자기파의 위상이 동위상이라는 뜻이다. 평면파는 평면에서 위상이 항상 같기 때문에 [그림 1, 2]처럼 위상을 표현하는 무한 평면이 전자기파 진행 방향으로 움직여야 한다.

[그림 1] 균일 평면파의 파면(출처: wikipedia.org)

[그림 2] 균일 평면파의 진행 모습(출처: wikipedia.org)

하지만 착각하면 안된다. 평면파는 파면이 평면이므로 전기장(electric field)과 자기장(magnetic field)이 무한 평면에 걸쳐 존재하므로 포인팅 정리(Poynting's theorem)에 의해 평면파가 실어나르는 평균 전력이 무한대가 된다. 하지만 평균 전력이 무한대인 이런 일은 물리계에서 발생할 수 없으므로, 평면파는 실제로 존재하지 않는 상상속에만 있는 이상적인 파동이 된다. 그러면 존재하지도 않는 파동을 왜 배울까? 첫째 이유는 평면파가 다른 어떤 파동보다 단순하여 쉽기 때문이다. 둘째 이유는 푸리에 변환 기법(Fourier transform technique)을 이용하면 임의의 파동을 평면파의 합으로 나타낼 수 있기 때문이다.

평면파를 이해하려면 그 공식을 한 번 유도해 보기가 가장 쉬운 방법이다. 우리의 시작점은 맥스웰 방정식(Maxwell's equations)이다. 편하게 생각하기 위해 공간에 원천(source)은 없다고 가정하고 전기장의 파동 방정식(wave equation)을 유도하면 다음과 같다.

                         (1)

식 (1)에 페이저(phasor)를 적용하면 시간 변화가 주파수로 바뀐 페이저 기반 파동 방정식을 얻을 수 있다.

                         (2)

여기서 파수(wavenumber)와 라플라시안(Laplacian)은 다음처럼 정의한다.

                          (3)

                         (4)

다음으로 $x, y$축으로는 변화가 없고[$\partial f/\partial x$ = $\partial f/\partial y$ = $0$] 오직 $z$축으로만 변한다고 생각한다. 그러면 식 (2)에서 3차원으로 표현된 파동 방정식을 1차원으로 단순하게 생각할 수 있다.

                         (5)

그러면 미분 방정식(differential equation) (5)를 어떻게 풀까? 미분해도 자기 자신이 되는 지수 함수(exponential function)를 식 (5)에 대입하면 식 (5)가 쉽게 풀린다.

                         (6)

여기서 미지수인 $k_z$를 미분 방정식에 집어넣어 $k_z$ = $\pm k$로 결정한다. 여기서 답이 $\pm k$이며 2개라는 부분이 재미있다. 파수 $+k$는 $+z$축으로 진행하는 파동, $-k$는 $-z$축으로 진행하는 파동을 뜻한다. 파수 $k_z$의 부호가 $z$축으로 진행하는 방향이 되는 이유는 시간 약속을 $\exp(-i \omega t)$로 선택하기 때문이다. 또한 $z$가 일정할 때 생기는 파면이 무한 평면이므로 식 (6)은 균일 평면파가 된다. 그런데 식 (5)를 풀 때 식 (6)처럼 답을 가정해서 푼다. 이런 접근은 정당한가? 물론 정당하며 맞는 접근법이다. 식 (5)는 상미분 방정식(ordinary differential equation)이기 때문에 미분 방정식의 존재성과 유일성(existence and uniqueness)이 존재해서 어떻게 풀더라도 답은 같다. 혹은 맥스웰 방정식의 유일성 정리(uniqueness theorem)에 의해 어떤 방법으로 풀더라도 답은 같다.

식 (6)의 접근법을 더 확장하면 3차원에 대한 평면파 방정식도 다음처럼 쉽게 얻을 수 있다.

                         (7)

식 (7)의 최종 결과는 매우 재미있다. 최종 결과가 구면(spherical surface)의 방정식이므로 파수를 구면 관점으로 생각한다.

[그림 3] 구의 표면(출처: wikipedia.org)

파수 $k_x, k_y, k_z$가 구면의 방정식을 만족하므로 가능한 해는 반지름이 $k$인 구면에 있기만 하면 된다. 구면은 모든 방향을 향하고 있으므로 전자파는 모든 방향으로 복사될 수 있다.

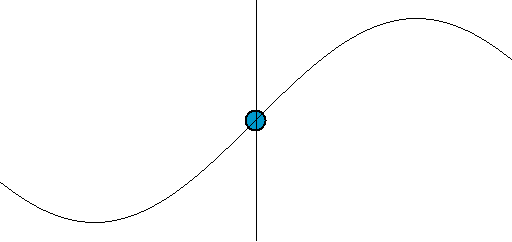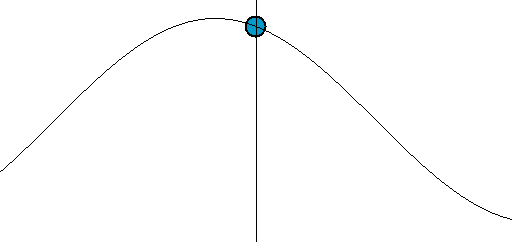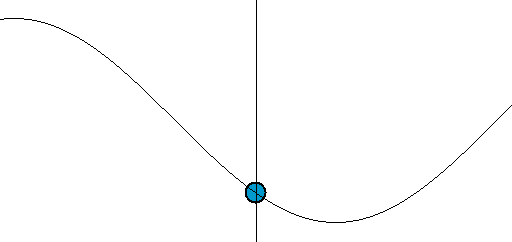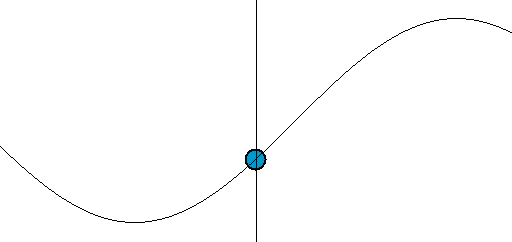
[그림 4] 파동의 움직임(출처: wikipedia.org)

[그림 1]에 있는 파면(波面, wavefront)에 기준값 개념을 적용하면 식 (7)의 전기장의 진행 방향을 예측할 수 있다. 쉽게 이해하기 위해 [그림 4]를 본다. 우리가 눈으로 특정한 파면[예시로써 꼭대기나 골짜기 등]을 추적해서 움직임을 이해하기 때문에, [그림 4]의 파동은 오른쪽에서 왼쪽으로 움직인다고 느낀다. 더 명확히 알기 위해 다음과 같은 파동 함수(wave function)를 생각한다.

             (8)

파면 위상의 기준값을 $0$이라 하면, $t$ = $0$일 때 $\Phi$ = $kr - \omega t$ = $k_x x_0 + k_y y_0 + k_z z_0$ = $0$을 만족해야 한다. 만약 $t$ = $\Delta t$가 되면, 기준값 $\Phi$ = $0$을 만족하기 위해 $k_x x_1 + k_y y_1 + k_z z_1$ = $\omega \Delta t$가 되어야 한다. 이 두 관계식을 빼면 다음 방정식을 얻는다.

                         (9)

여기서 $\bar k$는 파수 벡터(wavenumber vector: 전자파가 진행하는 위상을 표현하는 벡터)이다. 식 (9)의 좌변이 0보다 크려면 벡터 $\bar r_1 - \bar r_0$는 벡터 $\bar k$ 방향과 동일한 성분을 반드시 가져야 한다.[∵ 내적(inner product)의 특성을 생각하라.] 즉, $\bar r_1$ = $(x_1, y_1, z_1)$은 $\bar r_0$ = $(x_0, y_0, z_0)$로부터 $\bar k$ = $(k_x, k_y, k_z)$ 방향으로 진행한 형태가 된다. 이 개념이 헷갈리면 3차원 공간의 평면 방정식을 다시 고민해 보라. 이런 특성으로 인해 평면파는 벡터 $\bar k$ 방향으로 진행하며 파면은 무한 평면이 된다. 그래서 전자파의 공간적 진행을 연구하는 사람들은 $\exp(-i \omega t)$ 시간 약속을 주로 사용한다.

식 (9)를 조금 더 직관적으로 보려고 3차원이 아닌 1차원 파동 $e^{\pm i k z}$으로 간략화한다. 이 파동은 부호에 따라 $\pm z$축으로 진행한다. 예를 들어, $+z$축을 따라 $\Delta z$만큼 더 진행한 파동은 $e^{i k (z + \Delta z)}$ = $e^{i k z} e^{i k \Delta z}$로 기술된다. 반대 방향으로 $\Delta z$만큼 전파하는 파동은 $e^{-i k (z - \Delta z)}$ = $e^{-i k z} e^{i k \Delta z}$이다. 양방향 모두 추가적인 위상 항은 진행 방향에 관계없이 $e^{i k \Delta z}$로 나온다. 왜냐하면 시간 약속에 따라 $e^{-i \omega \Delta t}$가 나오므로 합산 기여분이 $e^{i (k \Delta z - \omega \Delta t)}$로 계산되기 때문이다. 여기서 $\Delta t$는 $\Delta z$를 갈 때 소요되는 시간이다.

3차원 평면파를 미분 관점으로 보면 재미있는 관계를 얻을 수 있다. 먼저 평면파를 $x, y, z$에 대해 미분한다.

                         (10)

식 (10)을 페이저 관점으로 접근하면 미분 연산자 나블라(nabla: $\bar \nabla$)를 벡터로 치환할 수 있다.

                         (11)

그러면 평면파인 경우 미분 방정식인 맥스웰 방정식은 아래처럼 단순한 벡터 방정식이 된다.

                         (12)

식 (12)는 평면파의 성질을 아주 쉽게 증명할 수 있게 해준다.

[그림 5] 평면파의 진행 모습(출처: wikipedia.org)

파수 벡터와 전기장의 내적이 0이므로 파수 벡터와 전기장은 서로 수직이다. 또한, 식 (9)에서 파수 벡터의 방향이 전자파가 진행하는 방향이므로 [그림 5]처럼 전기장[그림 5의 빨간색 선]은 진행 방향에 반드시 수직이다. 자기장[그림 5의 파란색 선]도 전기장과 동일한 성질이 성립한다. 식 (12)의 둘째식과 넷째식에서 다음도 유도할 수 있다.

                         (13)

여기서 $\eta$는 고유 임피던스(intrinsic impedance)이다. 고유 임피던스는 전자기장이 존재하는 매질[정확히는 유전율과 투자율]의 비율이다.

[그림 6] 허공(출처: wikipedia.org)

식 (13)은 전기장과 자기장의 비율인 파동 임피던스(wave impedance)가 고유 임피던스 $\eta$로 일정함을 의미한다. 진공 중에서 계산하면 고유 임피던스 혹은 파동 임피던스는 약 377 Ω[고상하게 $120 \pi$로 표현하기도 하지만 이 값도 근사이다.]정도가 된다. 하지만 착각하면 안된다. 전기장과 자기장의 비율 단위가 저항이라 해서 공간에 저항이 존재하지는 않는다. 눈을 들어 허공을 바라봐라. 아무것도 없다. 다시 말해, 전기장과 자기장의 비율로 정하는 파동 임피던스는 평면파인 경우 상수인 고유 임피던스가 된다. 또한 식 (12)에서 전기장, 자기장, 진행 방향[포인팅 벡터(Poynting vector) 방향]이 서로 수직임을 볼 수 있다. 따라서, 전기장과 자기장의 크기와 방향이 벡터 관점에서 서로 종속이다.

[그림 7] 구면파의 진행 모습(출처: wikipedia.org)

실제로 현실에 존재하는 파동은 [그림 5]의 평면파가 아닌 [그림 7]의 구면파(spherical wave)이다.[∵ 3차원 그린 함수(Green's function)를 풀어보면 쉽게 알 수 있다.] 관측점(observation point)이 구면파가 발생한 원천점(source point)에서 매우 멀면[혹은 원역장(far field) 조건이면] 이 파동은 평면파로 근사할 수 있다. 예를 들면, [그림 8]처럼 태양에서 발생한 빛이 지구에 오면 이 빛은 평면파로 간주할 수 있다.

[그림 8] 태양에서 오는 빛(출처: wikipedia.org)

구면파가 멀어지면 평면파로 근사 가능한 이유는 아래 식을 보면 쉽게 알 수 있다.

                     (14)

여기서 $r_0$는 첫번째 관측점 거리, $r_1$은 두번째 관측점 거리, 원천점은 $(0, 0, 0)$, $r_0$는 원천점에서 매우 멀다고 가정한다. 식 (14)를 이용해 구면파를 평면파로 근사화하면 다음과 같다.

                         (15)

여기서 분모에 있는 $4 \pi r$은 구면파에 대한 그린 함수(Green's function) 표현식으로 얻는다. 식 (15)에서 분모는 $r_0$로 근사화하고 지수 함수 부분은 남겨둔 이유가 무엇일까? 사실 원점에서 매우 멀어지면 $r_0$나 $r_1$은 서로 유사하다. 하지만 지수 함수 부분은 위상(phase)에 해당되므로, 얼마나 값이 큰지는 중요하지 않고 360˚ 범위 내에서 얼마만큼 변하는지가 중요하다. 그래서, 위상을 근사화할 때는 반드시 식 (14)를 이용해야 한다.

이론적으로 균일 평면파를 만드는 방법은 두 가지이다. 먼저 식 (15)처럼 점 원천(point source)을 무한대에 두고 측정하면 평면파가 된다. 즉, 특정 평면에 대해 점 원천이 만드는 전자파의 위상을 재면 평면으로 측정된다. 하지만, 원천이 무한대에 있기 때문에 전자기파의 크기는 $1/r$ 비율로 떨어진다.[∵ 구면파의 전력은 구의 표면에 있다. 구의 표면적은 $4 \pi r^2$이므로, 전자파 전력은 $1/r^2$ 비율로 떨어진다. 따라서 전자기장의 크기는 $1/r$로 감소한다.] 따라서 점 원천이 무한대에 있으면 관측점 전자기장이 0이 되므로 관측이 되려면 이 점 원천의 크기가 무한대로 발산해야 한다.[∵ $r$이 무한대로 갈 때 $A \times 1/r$이 유한한 값이 되려면 $A$는 무한대로 가야 한다.] 예를 들어서 태양에서 지구로 오는 빛은 근사적인 평면파이지만, 지구에서 무한히 떨어져 있고 무한대의 에너지를 가진 별이 쏘는 빛은 지구에서 이상적인 진짜 평면파가 된다. 물론 이런 빛은 현실에서 존재할 수 없다. 평면파를 만드는 또 한 가지 방법은 전류(electric current) 혹은 자류(magnetic current)를 무한 평면에 무한히 배치하기이다. 이 개념은 식 (16)에 있는 표면 등가의 원리(surface equivalence principle)로 쉽게 증명할 수 있다.

                        (16)

여기서 $\hat n$은 $\bar E_2$, $\bar H_2$가 정의된 영역에 수직으로 들어오는 단위 벡터[혹은 닫힌 영역에 대한 법선 벡터(normal vector: 기준 방향은 닫힌 영역을 뚫고 나가는 방향)의 반대 방향]이다. 식 (16)에서 $\bar E_2, \bar H_2$를 평면파라고 하면 그 원천은 전자기장 $\bar E_2, \bar H_2$처럼 무한 평면에 동위상으로 혹은 주기적 위상으로 존재하는 전류 혹은 자류여야 한다.

균일 평면파가 전파하는 매질에 손실이 있으면 파수 $k$는 다음과 같은 복소수(complex number)가 된다.

                        (17)

여기서 유전율(permittivity)은 $\epsilon$ = $\epsilon' +i \epsilon''$, 투자율(permeability)은 $\mu$ = $\mu' + i \mu''$, $\gamma$는 전파 상수(propagation constant), $\alpha$는 감쇠 상수(attenuation constant), $\beta$는 위상 상수(phase constant)이다. 식 (17)을 식 (6)에 대입해서 $+z$방향으로 진행하는 균일 평면파의 전기장을 표현한다.

                        (18)

평면파가 $+z$축으로 전파됨에 따라 전기장의 진폭은 $e^{-\alpha z}$만큼 줄어들고 위상은 $e^{i \beta z}$처럼 $+z$방향으로 움직인다.

[다음 읽을거리]
1. 평면파를 이용한 푸리에 변환 기법

2. 프레넬 방정식