3차원 자유 공간 그린 함수(3D Free-space Green's Function)

[경고] 아래 글을 읽지 않고 "3차원 자유 공간 그린 함수"를 보면 바보로 느껴질 수 있습니다.
1. 미분 방정식의 만병통치약: 그린 함수
2. 1차원 자유 공간 그린 함수
3. 2차원 자유 공간 그린 함수

4. 구면 조화 미분 방정식

[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.

1, 2차원 유도에 비슷하게 자기 벡터 포텐셜(magnetic vector potential)에 대한 파동 방정식을 전류 밀도(current density) $J_y$ = $J_z$ = $0$이라 가정하여 단순화한다.

                          (1)

그러면 식 (1)과 같이 스칼라 파동 방정식(scalar wave equation)이 식 (1)처럼 얻어진다. 식 (1)에 식 (2)의 라플라시안(Laplacian)을 대입하면 식 (3)에 있는 데카르트 좌표계(Cartesian coordinate system)의 3차원 스칼라 파동 방정식을 얻는다.

                         (2)

                         (3)

여기서 벡터 $\bar r$은 3차원 좌표점 $(x, y, z)$를 나타낸다.

[그림 1] 3차원 원천

[그림 2] 2차원과 3차원 데카르트 좌표계(출처: wikipedia.org)

[데카르트 좌표계 3차원 자유 공간 그린 함수]

                          (4)

[증명]

증명을 위해 먼저 디랙 델타 함수(Dirac delta function)를 아래와 같은 적분으로 표현한다.

                         (5)

식 (5)는 푸리에 변환의 완비성(completeness of Fourier transform)으로 쉽게 증명 가능하다. 식 (5)를 식 (3)에 대입하면 그린 함수는 다음처럼 표현할 수 있다.

           (6)

식 (6)을 계산하면 $g(z, z'; \zeta)$는 다음 1차원 자유 공간 그린 함수(1D free-space Green's function)에 대한 미분 방정식을 만족한다.

                         (7)

식 (7)의 최종 결과를 식 (6)의 첫째식에 대입하면 식 (4)가 증명된다.

______________________________

식 (4)는 푸리에 변환(Fourier transform)처럼 파수 영역(spectral domain)에서 표현되었으므로 파수 영역 그린 함수(spectral domain Green's function)라 부른다. 무한 적분으로 표현되어 어려워 보이기는 하지만 그린 함수를 미분(differentiation)하거나 적분(integration)하기는 쉽다.

텐서 이론(tensor theory)에 의해 맥스웰 방정식(Maxwell's equations)은 좌표 독립성(coordinate independence)을 가진다. 즉, [그림 2]의 데카르트 좌표계에서 답을 구한 결과와 다른 좌표계에서 구한 결과는 반드시 동일해야 한다. 그래서, 우리의 논의를 원통 좌표계(circular cylindrical coordinate system)로 옮겨본다.

[그림 3] 원통 좌표계의 표현(출처: wikipedia.org)

[원통 좌표계 3차원 자유 공간 그린 함수]

                          (8)

여기서 $H_0^{(1)}(\cdot­)$는 제1종 한켈 함수(Hankel function of the first kind)이다.

[증명]

식 (8)의 증명은 식 (4)와 동일하다. $z$축에 대한 델타 함수를 식 (5)처럼 바꾸고 원통 좌표계 2차원 자유 공간 그린 함수를 대입하면 식 (8)이 얻어진다.

______________________________

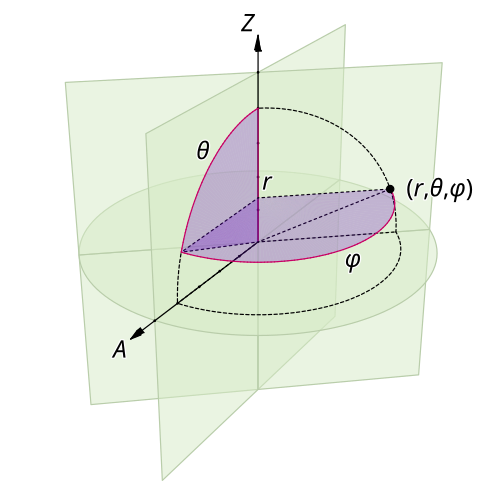
[그림 4] 구 좌표계의 표현(출처: wikipedia.org)

구 좌표계(spherical coordinate system)에 대해서는 매우 간단한 3차원 자유 공간 그린 함수를 얻을 수 있다.

[구 좌표계 3차원 자유 공간 그린 함수]

                          (9)

[증명]

문제를 간단히 만들기 위해 $(x', y', z')$ = $(0, 0, 0)$이라 가정한다.[혹은 원천이 원점에 있다.] 그러면 모든 방향으로 전자파가 골고루 복사되므로, 극고도각(極高度角, polar angle: $\theta$는 꼭대기부터 시작해 내려오기 때문에 일반 고도각과는 정의가 약간 다름) $\theta$ 방향과 방위각(方位角, azimuth) $\phi$ 방향으로는 전자파의 변동이 없다고 가정할 수 있다.[$\partial / \partial \theta$ = $\partial / \partial \phi$ = $0$] 따라서 식 (10)의 구 좌표계 라플라시안(Laplacian)은 식 (11)처럼 간략해진다.

                       (10)

                       (11)

그러면 식 (11)을 참고해서 해를 다음과 같이 가정할 수 있다.

                       (12)

식 (12)의 가정은 전자파의 복사 조건(radiation condition)을 이용하여 결정한다. 식 (12)에서 정해지지 않은 상수 $A$를 결정하면 증명은 끝난다. 식 (12)처럼 답을 완전히 가정해 푸는 접근법이 마음에 들지 않으면 해를 다음처럼 기술할 수도 있다.

                       (13)

식 (13)을 식 (12)의 마지막식에 대입하여 $f(r)$에 대한 미분 방정식을 구하면 다음과 같다.

                       (14)

식 (14)는 프로베니우스 방법(Frobenius method)을 적용할 수 있는 미분 방정식이므로 멱급수(power series)를 가정해 대입하면 식 (12)의 첫째식을 얻을 수 있다. 상수 $A$를 결정하기 위해 [그림 5]의 구를 생각한다.

[그림 5] 구(출처: wikipedia.org)

[그림 5]의 체적에 대해 식 (11)을 체적 적분하고 반지름 $r$을 $0$으로 보낸다.

                      (15)

여기서 증명을 위해 발산 정리(divergence theorem)를 이용한다. 그러면 원천이 $(x', y', z')$ = $(0, 0, 0)$에 있는 경우는 쉽게 증명된다. 다음 단계로 좌표 독립성을 사용해 $(x, y, z)$ = $(u-x', v-y', w-z')$을 만족하는 새로운 좌표계 $(u, v, w)$로 식 (12)를 좌표 변환한다. 이 결과는 식 (9)와 같아서 증명이 완성된다.[∵ $(u, v, w)$ = $(x', y', z')$에서 $(x, y, z)$ = $(0, 0, 0)$이 된다.]

______________________________

식 (9)는 적분 없이 공간 상의 좌표값만 있어서 공간 영역 그린 함수(space domain Green's function)가 된다. 최종 표현식은 간단하지만, 구 좌표계로 쓰여진 식 (9)를 직접 적분하기는 까다롭다. 이 경우는 데카르트 혹은 원통 좌표계로 기술된 식 (4)나 (8)을 대신 쓸 수 있다.

세 가지 다른 방법으로 증명을 해서 재미있는 결과를 얻었다. 우리의 증명을 서로 연결하면, 이중 적분이나 한켈 함수의 적분을 매우 간단한 식 (9)로 바꿀 수 있다.

                      (16)

식 (16)은 바일 항등식(Weyl identity)이라 부른다. 또한 식 (8)과 (9)를 서로 비교하면 다음 적분을 얻을 수 있다.

                      (17)

식 (16)과 같은 결과를 주지만 피적분 함수가 다른 식 (17)은 2차원 바일 항등식(2D Weyl identity)으로 증명하기도 한다.

[한켈 변환 이용한 3차원 자유 공간 그린 함수]

                         (18)

여기서 $k^2$ = $\kappa^2 + \zeta^2$, $|\bar \rho - \bar \rho'|$ = $\sqrt{(x-x')^2 + (y-y')^2}$이다.

[증명]

한켈 변환(Hankel transform)으로 얻은 2차원 디랙 델타 함수를 도입한다.

                      (19)

                      (20)

식 (20)을 이용해서 3차원 자유 공간 그린 함수를 다음과 같이 정의한다.

                      (21)

식 (21)을 식 (3)에 대입하고 원통 좌표계에 대한 라플라시안을 사용한다.

        (22)

식 (22)를 식 (7)처럼 연산하면 식 (18)이 쉽게 증명된다.

______________________________

식 (18)은 전자파의 산란 해석에 자주 등장해서 좀머펠트 항등식(Sommerfeld identity)이란 이름이 붙어있다. 당연한 예측이지만 식 (18)의 제안자는 좀머펠트Arnold Sommerfeld(1868–1951)이다. 좀머펠트 항등식의 피적분 함수를 베셀 함수에서 한켈 함수로 바꾸어 표현할 수도 있다.

                      (23)

여기서 한켈 함수의 해석적 연속(analytic continuation)에 의해 음의 실수축보다 약간 위로 적분 구간을 선택한다.

[공진형 3차원 자유 공간 그린 함수]

                         (24)

[증명]

식 (5)를 써서 모든 디랙 델타 함수를 푸리에 변환 형태로 바꾼 후, $x, y, z$에 대한 푸리에 변환 $\iiint (\cdot)e^{-i(\xi' x + \eta' y + \zeta' z)}\,dxdydz$를 다시 적용해서 $A$를 결정다.

             (25)

여기서 $(2 \pi)^3 A$는 $g(\bar r, \bar r'; k)$의 3차원 푸리에 변환이다.

______________________________

공진기(resonator)처럼 식 (24)는 $k^2$ = $\xi^2 + \eta^2 + \zeta^2$에서 특이점을 가져서 공진형 그린 함수(resonant Green's function)라 불린다.

[구면 조화 함수 이용한 3차원 자유 공간 그린 함수]

                         (26)

여기서 $Y_n^m(\theta, \phi)$는 구면 조화 함수(spherical harmonics)이다.

[증명]

구 좌표계에서 그린 함수 $g(\bar r, \bar r'; k)$가 만족하는 편미분 방정식은 다음과 같다.

             (27)

그린 함수의 도약 조건(jump condition)을 사용할 수 있도록 식 (27)의 첫째식에 $r^2$을 곱해서 정리한다.

                      (28)

식 (28)에 구면 조화 함수의 완비성을 써서 $g(\bar r, \bar r'; k)$를 구면 조화 함수의 무한 급수로 나타낸다.

                      (29)

                      (30)

             (31)

식 (31)에 구면 조화 함수의 직교성을 적용해서 $R_{nm}(r)$에 대한 미분 방정식만 뽑아낸다.

                      (32)

여기서 $g_n(r, r'; k)$는 구 좌표계에 대한 1차원 그린 함수이다. 식 (32)는 분명한 구면 베셀의 미분 방정식이기 때문에, 1차원을 위한 그린 함수 기법으로 $g_n(r, r'; k)$를 다음과 같이 결정한다.

                      (33)

여기서 $A$는 도약 조건의 상수이며, 구면 베셀 함수의 함수 행렬식을 이용해 계산된다. 마지막으로 식 (32), (33)을 식 (30)에 대입해서 식 (26)을 완전하게 유도한다.

______________________________

식 (26)은 다소 복잡해보이지만 구형을 가진 물체의 산란 특성을 계산할 때에 매우 유용한 관계식이다.

[다음 읽을거리]
1. 전자파의 복사 조건