적분법(積分法, Integration)의 의미

[경고] 아래 글을 읽지 않고 "적분법의 의미"를 보면 바보로 느껴질 수 있습니다.
1. 미분법의 의미
2. 극한과 연속성의 의미
3. 적분형 평균값의 정리
4. 조임 정리

[동영상]
1. Derek Owens - Math and Physics: Calculus - The Fundamental Theorem of Calculus

[리만 적분의 정의]

적분법을 쉽게 생각하려면 미분법의 반대라고 생각하면 된다. 마치 덧셈의 역연산은 뺄셈, 곱셈의 역연산은 나눗셈으로 생각하는 방식과 비슷하다. 하지만 적분법에는 이런 개념 이상의 의미가 있다.

[그림 1] 구간을 나누어 면적을 구하는 방법(출처: wikipedia.org)

[그림 1]에 표시하는 특정 곡선이 그리는 궤적[빨간색 곡선]에 대한 면적[회색 사각형]을 구할 때 적분법이 유용하게 사용될 수 있다. 이런 개념은 뉴턴Isaac Newton(1643–1727)과 라이프니츠Gottfried Wilhelm Leibniz(1646–1716)가 미적분법을 고안했을 때부터 잘 알려져 있었다. 그런데 적분을 하면 왜 면적을 얻을 수 있는가? 여기에 대한 진지한 고민이 적분법에 대한 이해를 도울 수 있다. 아래 식 (1)은 [그림 1]의 곡선이 표현하는 면적을 구하는 근사 수식이다. 

                 (1)

여기서 $x_n$은 면적을 구하기 위해 적분 구간을 나눈 점, $t_n$은 닫힌 세부 구간 $[x_{n}, x_{n+1}]$ 사이에 있는 임의점이다. 점 $x_n$은 아래 순서를 만족한다.

                  (2)

식 (1)이 근사가 아닌 정확한 적분이 되려면 식 (3)과 같이 $N$이 무한대로 가야 한다.

             (3)

여기서 $N$이 증가하면 이산적인 값 $t_n$은 연속적인 값 $x$가 된다. 왜냐하면 수열의 시작점($a$)과 끝점($b$)이 고정된 상태에서 수열의 수($N$)가 증가하기 때문에 수열 원소 간의 간격이 반드시 $0$으로 가야 한다. 수열 원소의 간격이 $0$에 무한히 근접하므로 닫힌 구간 $[x_n, x_{n+1}]$ 사이에 있는 $t_n$은 임의의 $\epsilon > 0$에 대해 $|t_n - x| < \epsilon$을 만족할 수 있다. 따라서, 수열 $t_n$이 $x$에 수렴하기 때문에 $t_n$을 연속적인 값으로 생각할 수 있다. 다만 식 (14)와 같은 이상한 경우가 있기 때문에 수열이 어떤 연속적인 값에 수렴한다 할지라도 실수의 완비성(completeness of real number)을 자동적으로 만족하지는 않는다. 그런데 식 (3)의 좌변과 우변이 같음은 첫눈에 이해가 되지는 않는다. 왜냐하면 식 (3)의 좌변은 부정적분(不定積分, indefinite integral: 미분의 역연산)을 기반으로 정적분(定積分, definite integral) 정의하고 있고, 식 (3)의 우변은 면적 개념을 이용해 정적분을 정의하기 때문이다. 이런 관계를 이해하려면 바보 같지만 놀라운 혜안이 필요하다. 뉴턴과 라이프니츠가 했던 위대한 착각을 흉내내 피적분 함수(被積分函數, integrand)인 $f(x)$가 어떤 함수 $F(x)$의 미분이라 가정한다. 여기서 $F(x)$를 원시 함수(原始函數, primitive function) 혹은 역도함수(逆導函数, antiderivative)라 부른다. 만약 $f(x)$를 $F(x)$의 미분으로 바꾸면 어떻게 되는지 식 (3)을 변형해본다. 간단한 계산을 위해 $x_{n+1} - x_n$ = $\Delta x$ = $(b - a)/N$, $t_n$ = $(x_{n+1} + x_n)/2$으로 둔다. 그러면 근사적으로 식 (4)가 성립한다.

               (4)

식 (4)가 근사식이 되는 이유는 $f(t_n) \ne \Delta F(t_n)/ \Delta x$이기 때문이다. 하지만 $N$이 무한대로 가면 식 (4)는 등식이 된다. 이런 개념을 사용하면 적분 과정은 곡선이 둘러싸고 있는 면적을 구하는 절차임을 쉽게 이해할 수 있다. 식 (4)의 방법론은 코쉬Augustin-Louis Cauchy(1789–1857)가 기초를 마련하고 리만Bernhard Riemann(1826–1866)이 확립했다[1]. 이 개념은 식 (3)의 우변에 정의한 리만 적분(Riemann integral)에서 매우 중요하다. 리만 적분은 적분 구간을 식 (2)처럼 나누고 이 세부 구간에 존재하는 임의의 $t_n$에 대한 함수값의 무한 합(infinite sum)이 항상 하나의 값으로 수렴하는 적분이다[1]. 식 (4)처럼 무한 합이 아닌 유한 합인 경우는 리만 합(Riemann sum)이라 한다. 리만 적분을 좀 더 수학적으로 살펴본다. 식 (4)의 유도에서 자명하다고 가정한 조건은 두 가지이다.

• 첫째, $F(x)$를 미분하면 $f(x)$가 되며 이 원시 함수 $F(x)$는 존재한다.

• 둘째, $\Delta x$를 줄이기 위해 식 (4)의 $N$이 무한대로 가면 적분으로 수렴한다.

이 두 명제를 각각 증명해본다.

[미적분학의 제1 기본 정리(the first fundamental theorem of calculus)]

함수 $f(x)$가 닫힌 구간 $[a, b]$에서 연속이고 $F(x)$가 닫힌 구간 $[a, b]$에서 식 (5)와 같이 정의되면, $F(x)$는 닫힌 구간 $[a, b]$에서 연속이며 열린 구간 $(a, b)$에서 미분 가능하고 $dF(x)/dx$ = $f(x)$가 성립한다.

                                             (5)

여기서 $F(a)$ = $0$이다.

[증명]

닫힌 구간 $[a, b]$에 있는 임의의 두 점을 $x_0$, $x_0 + \Delta x$라 한다. 그러면

                  (6)

식 (6)의 마지막 줄에서 두 구간을 합칠 수 있는 이유는 아래 식 (16), (17)에 증명되어 있다. 적분형 평균값의 정리(mean value theorem for integration)에 의하면 닫힌 세부 구간 $[x_0, x_0 + \Delta x]$에 존재하는 적당한 $c$에 대해 다음 식 (7)이 반드시 성립한다.

                   (7)

식 (6)과 (7)을 결합하면

                   (8)

$\Delta x$를 0으로 한없이 가까이 가게 하면 식 (8)의 좌변은 미분형이 된다.

               (9)

식 (8)의 우변은 $x_0 \le c \le x_0 + \Delta x$이 성립하므로 조임 정리(squeeze theorem)에 의해 식 (9)의 둘째 줄이 증명된다. $f(x)$가 연속이므로 $F(x)$의 미분은 존재하여 $F(x)$는 미분 가능하다. 또한, $F(x)$가 미분 가능하므로 당연히 연속 조건을 만족한다.

______________________________

[미적분학의 제2 기본 정리(the second fundamental theorem of calculus)]

함수 $f(x)$가 닫힌 구간 $[a, b]$에서 리만 적분 가능하고 $dF(x)/dx$ = $f(x)$가 성립하면 식 (10)을 만족한다.

                       (10)

[증명]

식 (10)에 소개한 적분 정의는 식 (3)과 동일하므로, 식 (4)를 이용하여 위 명제를 증명한다. 적분형 평균값의 정리인 식 (8)을 식 (4)에 적용하면 다음과 같다.

                (11)

여기서 $\Delta x_n$ = $x_{n+1} - x_n$이다. 식 (11)에서 $\Delta x_n$을 줄이기 위해 $N$을 무한대로 보내는 극한을 취한다

                  (12)

함수 $f(x)$가 리만 적분 가능하면, 식 (12)의 둘째 줄에 있는 극한이 존재한다. 그리고 함수 $F(x)$의 차이는 $N$과는 관계없는 값이므로 식 (10)이 증명된다.

______________________________

위의 정리 증명에서 평균값의 정리를 쓰지 않고 극값의 정리(extreme value theorem)를 쓰면 다르부 적분(Darboux integral)에 도달하게 된다. 이 적분은 다르부Jean Gaston Darboux(1842–1917)가 식 (3)의 우변에 있는 리만 적분을 더 명확하게 정의하기 위해 사용한 개념이다.

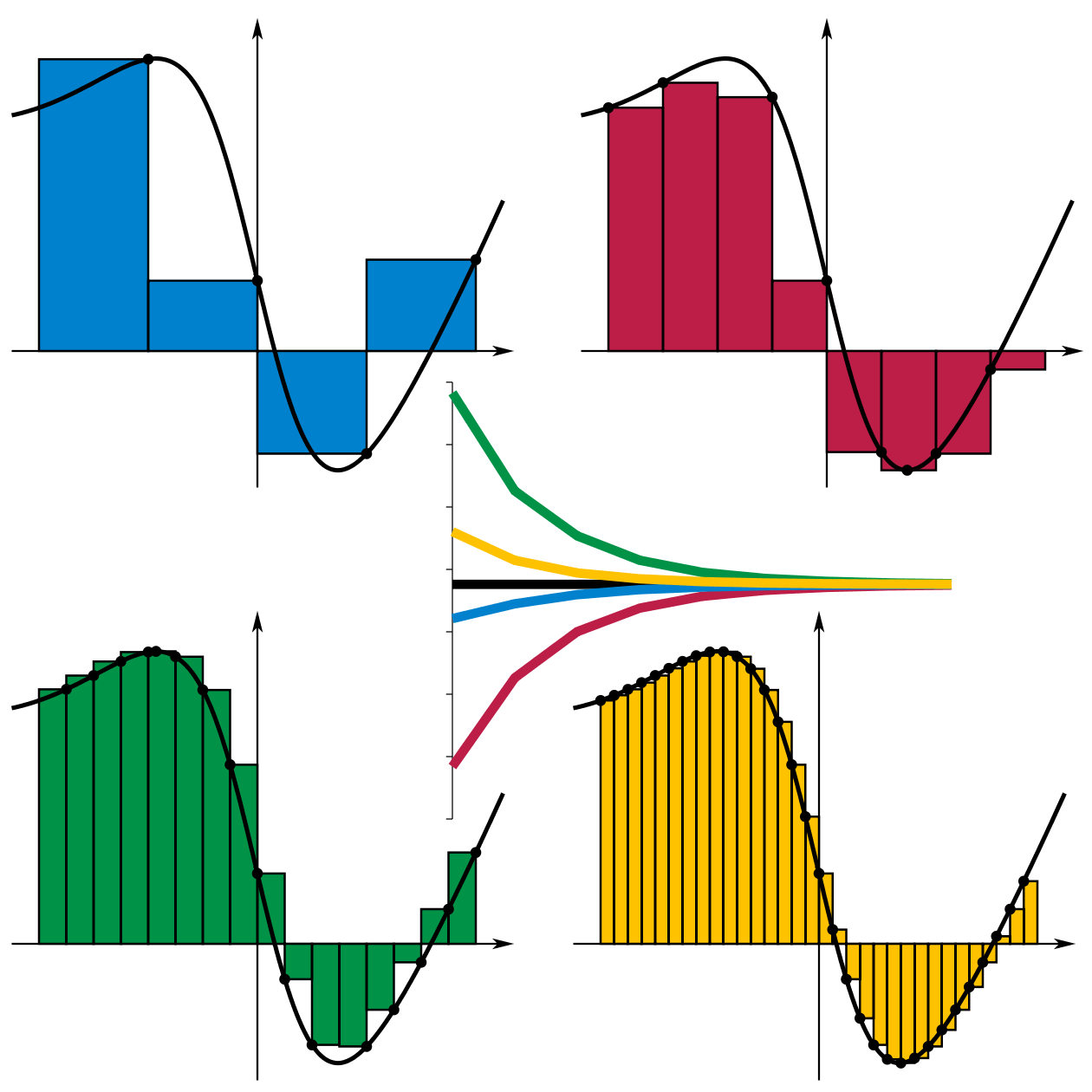
[그림 2] 리만 적분의 실제적인 예(출처: wikipedia.org)

식 (3) 우변의 리만 적분이 명확하지 않은 이유는 뭘까? 함수값을 정의하기 위한 $t_n$이 정해지지 않았기 때문이다. 리만 적분에서는 어떠한 $t_n$을 정의하든지 무한 합이 수렴해야만 리만 적분 가능(Riemann integrable)하다고 말한다. 예를 들어 [그림 2]를 본다. 초록색은 최대값, 빨간색은 최소값, 파란색은 오른쪽 값, 노란색은 왼쪽 값이 되도록 $t_n$을 선택한다. 임의의 $t_n$이라는 말에 명확성이 포함되지 않기 때문에[혹은 리만 적분을 계산할 때 항상 임의의 $t_n$에 대해 수렴함을 증명해야 하기 때문에] 다르부는 최대값과 최소값 개념을 이용하여 리만 적분을 식 (13)에 제시한 다르부 적분으로 다시 정의했다.

          (13)

여기서 세부 구간 $[x_n, x_{n+1}]$의 $t_n^\min$과 $t_n^\max$는 극값의 정리로 구한다. 사실 식 (3)의 리만 적분과 식 (13)의 다르부 적분은 서로 등가이다. 즉, 리만 적분 가능이면 $t_n$을 택할 때 항상 최대값이나 최소값이 되도록 할 수 있다. 그러면 리만 적분의 정의에 의해 적분이 동일한 값으로 수렴하므로, 다르부 적분 가능이 성립한다. 반대로 다르부 적분 가능하다면 식 (13)의 좌변과 우변이 한 값으로 수렴하므로, 조임 정리(squeeze theorem)에 의해 임의의 $t_n$에 대한 적분이 리만 적분과 같은 값으로 수렴한다. 따라서 다르부 적분은 리만 적분 가능하다.

적분의 기본적인 특성은 제1과 제2 기본 정리를 이용해 파악할 수 있다. 하지만 식 (3)이나 식 (12)와 같은 적분으로 모든 함수에 대한 적분을 할 수 있는가? 모든 점에서 불연속인 디리클레 함수(Dirichlet function) ${\bf 1}_\mathbb{Q}(x)$를 $f(x)$로 둔다.

            (14)

식 (14)에 있는 디리클레 함수는 $x$가 유리수(有理數, rational number)이면 $1$을 택하고, 무리수(無理數, irrational number)이면 $0$을 택한다. 식 (14)를 식 (3)에 넣고 $a$ = $0$에서 $b$ = $1$까지 적분하면 다음과 같다.

           (15)

식 (15)의 적분을 계산할 때 세부 구간을 나누는 기준점은 $x_n$ = $\Delta x \cdot n$ = $(1 - 0)/N \cdot n$으로 가정하고 $c_n$은 이 세부 구간에 있는 어떤 유리수라고 가정한다. 그러면 $c_n$이 유리수이기 때문에[예를 들면, $c_n$ = $(x_{n+1} + x_n)/2$] 최종 적분값은 반드시 $1$이 나와야 한다. 혹은 $c_n$을 무리수라고 하면[예를 들면, $c_n$ = $x_n + \Delta x \cdot (\sqrt{2}-1)$] 식 (14)에 의해 항상 $0$을 택하게 되어서 적분값은 $0$이 나온다. 하지만 $c_n$의 선택에 따라 적분값이 바뀌므로, 디리클레 함수는 리만 적분 가능하지 않다. 그러면 디리클레 함수를 적분할 수는 없을까? 유리수는 가산 집합(可算集合, countable set)이고 무리수는 비가산 집합(非可算集合, uncountable set)임을 칸토르Georg Cantor(1845–1918)가 증명했다는 사실을 기억한다. 비가산 집합은 가산 집합보다 농도가 무한대로 많기 때문에, 디리클레 함수의 적분값은 $1$이나 $0$이 아니라 항상 0이 되어야 타당하다. 그러면 리만 적분 자체가 틀렸는가? 아니다. 리만 적분의 적용이 틀렸다. 리만 적분이 적용되려면 유한한 구간에서 함수의 연속성(continuity)이 반드시 성립해야 한다. 식 (14)에 있는 함수 $f(x)$는 유한 구간에서 연속성을 만족하지 않기 때문에 리만 적분을 적용할 수 없다.[∵ 함수가 연속성을 만족하면 리만 적분값이 항상 하나의 값으로 수렴해야 하나 두 가지 값이 얻어질 수 있기 때문에 식 (14)의 함수는 어떤 세부 구간에서도 연속이 아니다.] 이런 리만 적분의 문제점에 대한 해결책이 르베그Henri Lebesgue(1875–1941)가 제안한 르베그 적분(Lebesgue integral)이다. 르베그는 간단하지만 기상천외한 방법으로 리만 적분을 변형했다. 르베그 적분을 통해 적분 가능성과 함수의 연속성을 분리시킬 수 있다. 이런 인간 지성의 궁극에서 수학의 아름다움을 본다. 

식 (5)에 제시한 미적분학의 제1 기본 정리에 의해, 연속 함수에서는 원시 함수 찾기와 리만 적분 가능이 동치이다. 하지만 원래 원시 함수와 리만 적분은 서로 다른 용어이다. 원시 함수는 미분해서 피적분 함수가 되는 함수이며, 적분은 면적을 계산하기 위해 적분 구간을 무한히 쪼개서 더하는 연산이다. 원시 함수와 리만 적분은 서로 정의가 다르지만, 함수 $f(x)$가 연속이라는 강력한 조건을 부가하면 항상 원시 함수를 찾을 수 있고[찾기 어려우면 테일러 급수(Taylor series)를 이용할 수도 있다.] 리만 적분도 가능하다. 그래서 원시 함수 찾기와 리만 적분 하기는 서로 같은 말처럼 쓰인다. 식 (13)에 있는 다르부 적분의 정의에 따라, 리만 적분 가능을 다음처럼 더 명확히 정의하기도 한다[2].

               (16)

여기서 $\epsilon$은 임의로 작은 양의 실수이다. 함수 $f(x)$가 연속이라면, 적분 구간을 줄여서 다음처럼 $D_n$을 원하는 만큼 줄일 수 있다. 따라서 $f(x)$는 리만 적분 가능하다.

      (17)

여기서 세부 구간을 충분히 줄여서 이 구간의 함수 최대값과 최소값 차이를 $\epsilon/(b - a)$보다 작게 만든다. 또한 적분 구간 $[a, b]$의 길이는 $b - a$로 설정한다. 만약 $f(x)$가 조각 연속(piecewise continuous)이며 불연속 위치에 생긴 함수값 차이를 $\Delta f$라 하면, $f(x)$는 다음처럼 여전히 리만 적분 가능이다.

                 (18)

여기서 $m$은 불연속 세부 구간을 제외해서 연속을 만족하는 모든 세부 구간을 표현하는 첨수, 불연속 세부 구간의 길이는 $\epsilon_1 / (|\Delta f| + 1)$로 설정, 연속 세부 구간의 길이는 식 (17)을 이용해 무한 급수의 합이 $\epsilon_2$보다 작도록 한다. 그러면 식 (16)의 급수 합을 임의의 양의 실수 $\epsilon$보다 항상 작게 만들 수 있다. 즉 함수에 불연속이 생기면 불연속의 크기만큼 세부 구간을 더 잘게 나누면 식 (16)의 급수 합을 계속 줄일 수 있기 때문에 조각 연속이더라도 리만 적분 가능하다. 다르게 보면, 연속 함수인 경우는 세부 구간을 줄이면 자연적으로 최대값과 최소값 차이가 줄어들어 식 (16)이 수렴한다. 하지만 조각 연속 함수는 불연속점에서 최대값과 최소값의 차이를 줄이지 못하기 때문에 구간을 더 많이 줄여야 한다.
조각 연속 조건을 더 약화시켜서 함수 $f(x)$를 유계라고만 가정하면 어떻게 될까? 해답을 찾기 위해 다음과 같은 함수 $F(x)$를 고려한다.

               (19)

여기서 $F(x)$는 $x$ = $0$에서 불연속이므로 $F(0)$ = $0$이라 두어 연속으로 만든다. 미분 측면에서 $F(x)$는 상당히 이상한 특성을 가지고 있다. 점 $x$ = $0$에서 $F(x)$의 미분은 존재하지만 $x$ = $0$ 근방에서 미분[= $\lim_{x \to 0} f(x)$]이 정의되지 않다. 먼저 미분 정의를 이용해 $F'(0)$을 계산하면 다음과 같다.

               (20)

식 (19)에 의해 $F(x)$의 미분인 함수 $f(x)$는 유계이지만 $x$ = $0$에서 불연속이다. 왜냐하면 $f(x)$는 $x$ = $0$ 근방에서 $-1$에서 $1$ 사이를 변하므로 분명히 유계이며, $x$ = $0$에서 함수값을 정할 수 없으므로 불연속이 된다. 따라서 $x$ = $0$에서 $F(x)$는 미분 가능하지만 $x$ = $0$ 근방에서는 미분 불가능하다. 함수 $F(x)$와 $f(x)$는 미분 관계이므로 $f(x)$에 대한 부정적분을 다음처럼 쓸 수 있다. 즉 $f(x)$에 대한 원시 함수를 $F(x)$로 정할 수 있다.

               (21)

원시 함수를 찾았지만 $f(x)$가 리만 적분 가능한지 결정하기는 매우 애매하다. 왜냐하면 적분은 [그림 2]처럼 면적을 찾는 연산이며 $x$ = $0$ 근방에서는 코사인 함수가 매우 빠르게 변할 수 있다. 그래서 적분 구간을 아무리 잘게 쪼개어도 쪼갠 만큼 함수값이 빠르게 변해서 적분을 표현하는 급수 합이 수렴하지 않을 수도 있다. 이런 경우는 리만 적분을 표현하는 식 (16)으로 증명해야 한다. 점 $x$ = $0$ 근방에서 세부 구간을 아주 잘게 나누면 코사인 함수$[= \cos (1/x)]$와 세부 구간 길이$[= \Delta x]$의 곱은 임의의 양의 실수 $\epsilon$보다 항상 작게 만들 수 있다. 따라서 식 (18)과 동일한 과정을 거치면 다음을 얻는다.

               (22)

즉 $x$ = $0$에서만 불연속이기 때문에 최대값과 최소값의 차이는 2가 되며 연속인 $x$ = $0$ 근방에서 세부 구간의 길이를 계속 줄여 $\epsilon_1$을 계속 작게 할 수 있으므로 식 (16)은 수렴한다. 따라서 식 (19)는 리만 적분 가능해서 다음처럼 기술할 수 있다.

               (23)

그러면 유계인 함수는 항상 리만 적분 가능할까? 유계와 적분 가능에 대한 의문을 적극적으로 고민한 수학자는 볼테라Vito Volterra(1860–1940)이다. 이에 대한 해답으로 1881년볼테라 21세, 조선 고종 시절에 볼테라는 [그림 3]과 같은 볼테라의 함수(Volterra's function)를 제안했다. 이외에도 볼테라는 볼테라 적분 방정식(Volterra integral equation)에도 큰 기여를 했다. 볼테라의 함수는 다음 성질을 가진다.

• 정의역은 $[0, 1]$이다.

• 볼테라의 함수는 연속이다.

• 볼테라 함수의 미분은 존재하며 유계이다.

• 볼테라 함수의 미분은 리만 적분 가능하지 않다.

[그림 3] 볼테라의 함수(출처: wikipedia.org)

위에 제시한 볼테라 함수의 성질을 증명하기 위해 [그림 3]과 같은 볼테라의 함수를 생성해본다. 전체적인 생성 방식은 [그림 4]의 스미쓰–볼테라–칸토르 집합(SVC 집합: Smith–Volterra–Cantor set)처럼 잘라진 공간[그림 4에서 검정색이 아닌 흰색 구간]에 식 (19)의 $F(x)$를 이동하여 배치하기와 같다.

[그림 4] 스미쓰–볼테라–칸토르 집합의 생성 방법(출처: wikipedia.org)

볼테라의 함수 $V(x)$에 대한 세부적인 생성 절차는 다음과 같다.

• 구간 $I$ = $[0, 1]$을 함수 식 (19)에 있는 $F(x)$를 변형해 채운다.

• 먼저 $F(x)$가 구간 $[0, 1/8]$에서 변할 때 $F(x)$의 최대값이 생기는 위치를 $x$ = $x_{1}$이라 한다. 그러면 $F'(x_1)$ = $0$이 된다.

• 최대점 $x_1$을 이용해 구간 $[0, 1/8]$에 정의한 함수 $f_1 (x)$는 다음처럼 표현된다.

                     (24)

• 함수 $f_1 (x)$를 $x$축에 대해 대칭시키고 평행 이동해서 구간 $[1/8, 1/4]$에 함수 $f_1 (1/4 - x)$를 정의한다. 이 두 함수를 합쳐서 새로운 함수 $g_1(x)$[= $f_1 (x) + f_1 (1/4 - x)$]를 만든다. 그러면 $g_1(x)$의 정의 구간은 $[0, 1/4]$로 확장된다.

• 함수 $g_1(x)$를 $x$축으로 3/8[= 1/2 - 1/8]만큼 평행 이동하여 함수 $v_1(x)$[= $g_1(x - 3/8)$]를 만든다. [그림 3]의 중앙 부분에 보이는 함수가 $v_1(x)$이다.

• 함수 $v_1(x)$를 정의한 구간은 [그림 4]에 보이는 둘째 줄 흰색 부분과 같다.

• 다음으로 [그림 4]의 셋째 줄 흰색 부분에도 함수 $v_2(x)$를 정의한다. 함수 $v_1(x)$와 비슷하게 $v_2(x)$를 생성하지만, 구간 길이는 1/4 비율로 줄인다. 예를 들면 $f_2 (x)$는 구간 $[0, 1/32]$에서 정의한다. 이 구간에서 $f_2 (x)$가 최대값을 가지는 점을 $x$ = $x_2$라 한다. 함수 $f_2 (x)$는 식 (24)와 비슷하게 정의할 수 있다. 다만 [그림 4]에서 보듯이 $g_2(x)$는 두 개를 만들어서 구간 $[0, 3/8]$과 $[5/8, 1]$의 중심으로 각각 이동해야 한다. [그림 3]에서 좌우에 하나씩 보이는 모양이 $g_2(x)$를 평행 이동하여 $v_2(x)$로 정의한 함수이다.

• [그림 4]처럼 이 과정을 무한히 반복하여 $v_n (x)$를 생성하면 볼테라의 함수 $V(x)$를 다음처럼 표현할 수 있다.

                     (25)

식 (25)로 정의한 함수는 기본 모양이 식 (24)와 비슷하다. 그래서 함수 $V(x)$는 구간 $[0, 1]$에서 연속이며 미분 가능하다. 함수 $V(x)$를 미분한 $v(x)$[= $dV(x)/dx$]는 식 (19)에 의해 유계이다. 함수 $v(x)$는 임의의 구간 $[0, x_0]$에서 리만 적분 가능하지 않다. 여기서 $0 < x \le 1$. 이는 SVC 집합이 조밀한 곳이 없는 집합(nowhere dense set)에 속하기 때문이다. 상세히 설명하면, SVC 집합에서 서로 다른 두 점 $x, y$를 선택해본다. [그림 4]에서 검정색으로 표시한 영역에 있는 $x, y$를 아무리 간격을 좁혀 선택하더라도 구간 $[x, y]$를 만들 수 없다.

[그림 5] 칸토르 집합의 생성 방법(출처: wikipedia.org)

볼테라 함수의 리만 적분 불가능성으로 인해 [그림 4]의 SVC 집합을 꼼꼼하게 볼 필요가 있다. 더 잘 이해하기 위해 SVC 집합을 [그림 5]의 칸토르 집합(Cantor set)과 비교해본다. 칸토르 집합은 구간 $[0, 1]$을 삼등분해서 1/3 부분을 제거한다. [그림 4, 5]에서 남아있는 검정색 부분이 각각 SVC 및 칸토르 집합이다. 예를 들어, [그림 5]의 둘째 줄에 남는 구간은 $[0, 1/3]$과 $[2/3, 1]$이다. [그림 5]에 있는 과정을 계속 반복하면 남아있는 검정색 구간의 길이는 어떻게 될까? [그림 5]에서 잘라낸 부분을 먼저 생각해본다. 간단한 등비 급수이므로 다음처럼 계산한다.

               (26)

잘라낸 부분이 1이므로, 남아있는 구간의 길이는 신기하게도 0이 된다. 칸토르 집합은 구간의 길이가 0이며, 임의의 서로 다른 두 점을 어떻게 선택하더라도 연속된 구간을 만들 수 없다. 그래서 칸토르 집합도 조밀한 곳이 없는 집합이다. 식 (26) 계산에서 보듯이, 남아있는 구간 길이가 없기 때문에 이럴 수 있다고 생각할 수 있다. 비슷한 방식을 SVC 집합에도 적용해본다. 칸토르 집합과는 다르게 사등분해서 1/4만 남기기 때문에 잘라낸 부분의 길이는 다음과 같다.

               (27)

[그림 4]를 봐도 알 수 있듯이 SVC 집합은 잘라낸 길이[흰색]와 남아있는 길이[검정색]가 같다. 남아있는 길이가 분명 있는데도 SVC 집합은 조밀한 곳이 없는 집합이다. 이는 굉장히 특이한 결과이므로 증명을 해보자[3]. 먼저 [그림 4]에서 남아있는 세부 구간의 길이 $l_n$을 구해본다. 식 (27)에 의해 잘라낸 세부 구간의 전체 길이 $C_n$을 알기 때문에 $l_n$은 다음과 같다.

               (28)

[그림 4]처럼 자르기 연산을 $n$번 한 후에 만들어진 $2^n$개의 세부 구간[그림 4에서 검정색 선]을 생각한다. 세부 구간에 있는 서로 다른 두 점 $x, y$[$y > x$이며 같은 세부 구간에 있을 필요는 없다.]를 뽑고 두 점 사이의 길이를 $d$ = $y - x$라 한다. 자르기 연산을 계속 해나가면 적당한 $N$에 대해 $l_{n+N} < d$가 된다. 이러면 $x, y$ 사이에 $x, y$와 연결되지 않는 세부 구간이 생긴다. 그래서 $x, y$는 같은 세부 구간에 있을 수 없다. 이를 더 확장하면, SVC 집합은 자르기 연산을 무한 번 반복하기 때문에 세부 구간에 있는 어떤 두 점도 같은 구간에 절대 있을 수 없다. 다른 말로 하면 SVC 집합에 있는 서로 다른 두 점 $x, y$ 사이에는 $x, y$와 세부 구간이 다른 점 $z$가 항상 존재한다. 따라서 SVC 집합은 세부 구간의 길이는 있지만 조밀한 곳이 없는 집합이 된다.
SVC 집합에 대한 논의를 볼테라 함수에 다시 적용해본다. 볼테라 함수를 정의할 때 사용한 세부 구간은 SVC 집합의 세부 구간과 같다. 따라서 SVC 집합의 세부 구간의 끝점 위치에서 $V(x)$를 미분하면 항상 불연속이 된다. 이 불연속 점 근방에서 $v(x)$를 적분하려면 식 (16)처럼 세부 구간 $[x_n, x_{n+1}]$을 정의하고, 식 (22)처럼 세부 구간의 길이를 계속 줄였을 때 임의의 양의 실수 $\epsilon$보다 항상 작아야 한다. 하지만 SVC 집합의 특성으로 인해 구간을 아무리 줄이더라도 그 구간 안에는 불연속점이 존재한다. 예를 들어 적분 구간을 $x$ = $0$ 가까이 되도록 $[0, \Delta x]$로 잡으면 그 급수 합은 식 (22)처럼 되지 않고 다음처럼 표현된다.

             (29)

식 (29)에 의해 급수 합을 임의의 양의 실수 $\epsilon$ 보다 작게 잡을 수가 없다. 왜냐하면 $x$ = $0$ 근방에는 불연속점이 SVC 집합과 같이 계속 존재하기 때문에, 식 (22)처럼 불연속점의 구간은 줄이고 연속점의 구간은 늘려서 적분하기는 불가능하다. 그래서 볼테라 함수의 미분은 리만 적분 불가능이다. 정리하면 볼테라 함수의 미분과 관련된 적분은 다음처럼 쓸 수 있다.

               (30)

식 (3)에 정의한 리만 적분 관계식을 이용해서 다양한 적분 특성을 증명할 수 있다.

   1. 기본(basics)   

미분 공식과 식 (3)의 우변을 이용하면 다양한 적분 공식을 유도할 수 있다.

[$0$인 적분 구간]

               (1.1)

[증명]

정적분의 정의인 식 (3)에 의하면 닫힌 구간 $[a, a]$는 길이가 없으므로[$\Delta x$ = $x_{n+1} - x_n$ = $0$] $f(x)$가 유한하면 당연히 정적분값은 0이 되어야 한다.

______________________________

[반대 방향 적분 구간]

            (1.2)

[증명]

식 (3)에서 적분 구간을 거꾸로 바꾸면 $\Delta x$ = $x_{n+1} - x_n$의 부호가 바뀌어 정적분값도 부호가 바뀌어야 한다.

______________________________

[적분 구간의 연결]

         (1.3)

[증명]

두 적분을 식 (3)처럼 무한 합으로 바꾸고 적분 구간 $[a, b]$와 $[b, c]$를 식 (2)와 유사한 형식으로 서로 연결한다. 그러면 이 무한 합은 적분 정의에 따라 식 (1.3)의 우변과 같이 쓸 수 있다. 따라서 두 적분 구간을 하나로 합칠 수 있다.

______________________________

[선형 사상(線型寫像, linear mapping)]

          (1.4)

[증명]

식 (1.4)의 피적분 함수를 식 (3)에 대입하여 정리하면 식 (1.4)가 바로 나온다.

______________________________

식 (1.4)를 확장하여 여러 함수를 사용하는 유한 급수(finite series)에도 적분을 적용할 수 있다.

         (1.5)

식 (1.4)는 적분과 유한 합(finite sum)이 서로 교환될 수 있음을 보여준다.

[부분 적분(部分積分, integration by parts)]

          (1.6)

[증명]

적분은 미분의 역연산이므로 곱셈에 대한 미분 공식을 이용하여 식 (1.6)을 증명할 수 있다. 여기서 다음 기호를 사용한다.

             (1.7)
______________________________

[부등식]

                  (1.8)

[증명]

조건에 의해 항상 $g(x)-f(x) \ge 0$이다. 함수값이 $0$보다 큰 함수를 적분하면 정적분은 항상 $0$보다 크다. 즉 $\int_a^b [g(x) - f(x)]\,dx$ $\ge$ $0$이 성립한다. 이 결과에 식 (1.4)를 적용해서 식 (1.8)의 오른쪽 식을 얻는다.

______________________________

[정적분의 미분]

                  (1.9)

                  (1.10)

[증명]

식 (1.10)의 적분을 위해서 $x, t$에 대한 편미분(partial differentiation) 관계를 다음과 같이 설정한다.

                  (1.11)

식 (1.11)의 좌변과 우변을 $t$에 대해서 $a$에서 $x$까지 정적분한다.

                  (1.12)

다음 단계로 식 (1.12)의 첫째식을 $x$에 대해 미분한 후 식 (1.12)의 둘째식을 대입한다. 그러면 식 (1.10)이 증명된다.

                  (1.13)

여기서 완전 미분(exact differential)을 도입해 $F(x, x)$의 미분을 $dF(x, t) |_{t = x}$ = $\partial F(x, t)/ \partial x \cdot dx |_{t = x}$ $+$ $\partial F(x, t)/ \partial t \cdot dt |_{t = x}$처럼 구한다. 

______________________________

식 (1.10)은 볼테라 방정식(Volterra equation)이나 아벨의 적분 방정식(Abel's integral equation)에 활용된다.

   2. 이중 적분(double integral)   

[병진 대칭성(translational symmetry)]

               (2.1)

여기서 $u$ = $x-y$이다.

[증명]

매개변수 $u$ = $x-y$라 두고 식 (2.1)의 좌변을 정리한다.

                  (2.2a)

여기서 $F(x)$는 $f(x)$의 원시 함수이다. 식 (2.2a)의 마지막식을 각각 부분 적분한다.

                  (2.2b)

                  (2.2c)

식 (2.2b)와 (2.2c)를 빼서 식 (2.1)로 간략화한다.

______________________________

식 (2.1)은 자기 상관(autocorrelation)이 등장하는 관계식에 많이 쓰인다.

[참고문헌]

[1] B. Riemann, Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe (About the Description of a Function by a Trigonometric Series), 1853.
[2] D. M. Bressoud, "Wrestling with the fundamental theorem of calculus," Macalester College, Minnesota, Oct. 2003. (방문일 2010-07-08)
[3] J.-P. Merx, "The Smith Volterra Cantor set," Math Counterexamples, Nov. 2015. (방문일 2019-10-05)

[4] 김경화, "적분개념의 발달 (리만적분에서 르베그적분으로의 이행을 중심으로)", 한국수학사학회지, 제21권, 제3호, pp. 67–96, 2008년 8월.

[다음 읽을거리]
1. 미분 방정식의 의미

2. 리만–르베그 보조 정리

3. 연산 미적분학