[경고] 아래 글을 읽지 않고 "수치 적분"을 보면 바보로 느껴질 수 있습니다.

[그림 1] 사각형 규칙(rectangle rule)으로 수치 적분(출처: wikipedia.org)
리만 적분(Riemann integral)으로 만든 정적분(definite integral)을 수치적으로 계산하기 위해 면적을 다양한 방식으로 근사하는 방법을 수치 적분(numerical integration)이라 부른다. 수치 적분이란 명칭 대신 옛날 용어인 구적법(求積法, quadrature)을 쓰기도 한다. 수치 적분 중에서 가장 직관적인 방법은 면적을 작은 사각형으로 어림하는 사각형 규칙(rectangle rule) 혹은 중점 규칙(midpoint rule)다.
 (1)
(1)여기서 $x$ = $(a+b)/2$는 구간의 중점(midpoint)이다.

[그림 2] 사다리꼴 규칙(trapezoidal rule)으로 수치 적분(출처: wikipedia.org)
사각형 규칙보다 함수 $f(x)$에 더 가깝게 근사하는 방식은 [그림 2]처럼 미소 사다리꼴을 쓰는 사다리꼴 규칙(trapezoidal rule)이다.
 (2a)
(2a) (2b)
(2b)여기서 $x_k$ = $a+kh$; 세부 구간의 간격 $h$는 모두 동일하다.
1. 심슨의 규칙(Simpson's rule)
[그림 1.1] 구간을 나누면서 적용한 심슨의 규칙(출처: wikipedia.org)
심슨의 규칙(Simpson's rule)은 정적분의 피적분 함수 $f(x)$를 제2차 라그랑주 보간(Lagrange interpolation)인 $f(x)$ $\approx$ $L_2(x)$으로 근사한다.
 (1.1)
(1.1)여기서 $h$ = $\Delta x$ = $(b-a)/2$, $x_0$ = $a$, $x_1$ = $(a+b)/2$ = $a+h$, $x_2$ = $b$, $y_k$ = $f(x_k)$이다. 라그랑주 다항식(Lagrange polynomial) $l_k(x)$의 입력 변수를 $u$ = $x-x_1$로 전환한다.
 (1.2)
(1.2)여기서 $x_1 - x_0$ = $x_2 - x_1$ = $h$, $x_2 - x_0$ = $2h$이다. 식 (1.2)를 식 (1.1)에 넣고 정적분해서 심슨의 규칙을 완성한다.
 (1.3)
(1.3)식 (1.3)에 공통 인자로 $1/3$이 나와서, 식 (1.3)을 심슨의 1/3 규칙(Simpson's 1/3 rule)으로 이름 붙이기도 한다.
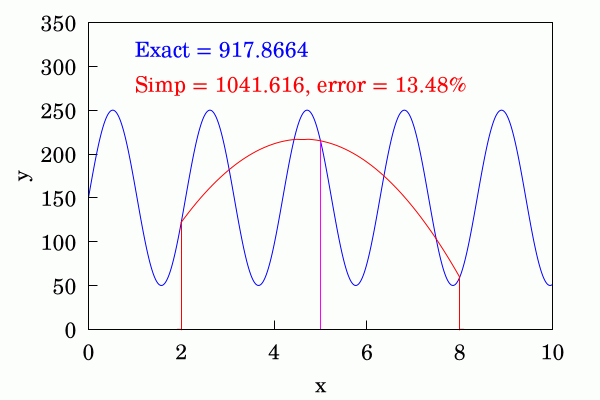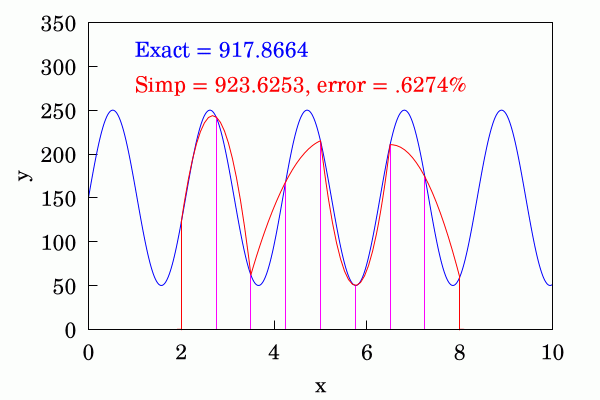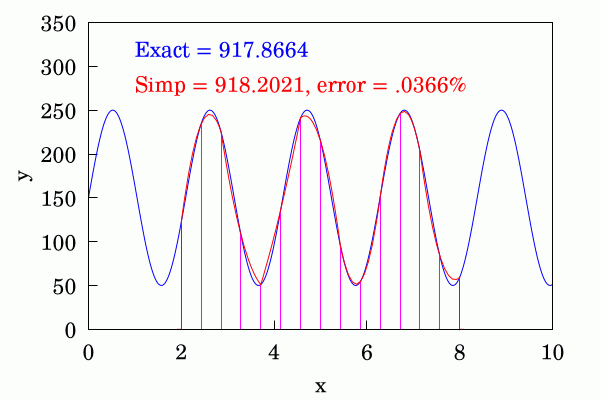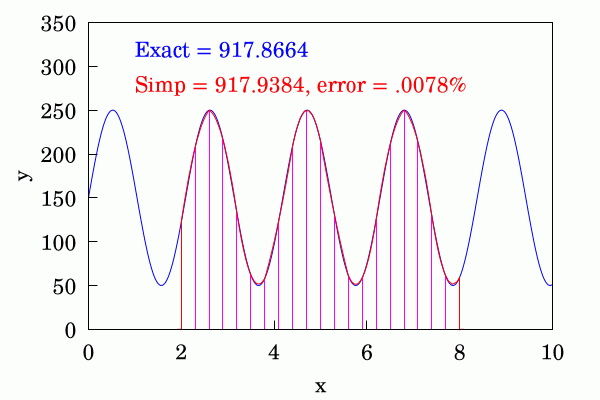
식 (2b)처럼 구간을 세밀하게 나누어 세부 구간의 간격을 $h$ = $(b-a) \mathbin{/}(2n)$이 되게 한다.
 (1.4)
(1.4)여기서 $x_0$ = $a$, $x_{2n}$ = $b$, $x_k$ = $a + kh$; 계산에 쓰는 함수값의 개수는 $2n+1$이다.
2. 뉴턴–코츠 공식(Newton–Cotes formula)
심슨의 규칙을 제$n$차 라그랑주 보간 $L_n(x)$로 일반화해서 수치 적분하는 방법은 뉴턴–코츠 공식(Newton–Cotes formula)이 된다.
 (2.1)
(2.1)여기서 $x_k$ = $a+kh$, $h$ = $(b-a)/n$; $w_k$는 정적분의 속성을 가진 가중치(weight)이다. 만약 식 (2.1)에서 $n$ = $2$인 경우는 심슨의 1/3 규칙이 된다.
뉴턴–코츠 공식은 매우 유용한 도구이지만 조심할 점이 있다. 식 (2.1)처럼 적분을 할 때 라그랑주 보간을 쓰기 때문에, 고차 라그랑주 다항식을 쓸수록 $x$ = $a$와 $b$ 근방에서 룽에 현상(Runge's phenomenon)이 발생해 적분 결과가 발산할 수 있다. 그래서 피적분 함수가 충분히 부드러워서 고계 미분[고차 미분도 쓰이지만 용어의 일관성을 위해 고계를 채택]이 유한하다는 가정이 꼭 필요하다.
[다음 읽을거리]
댓글 없음 :
댓글 쓰기
욕설이나 스팸글은 삭제될 수 있습니다. [전파거북이]는 선플운동의 아름다운 인터넷을 지지합니다.