1. 열 방정식


[그림 1] 푸리에 급수를 이용한 톱니파의 표현(출처: wikipedia.org)
통신 이론(communication theory)을 공부한 사람이면 누구나 아는 개념이 아래의 기함수(奇函數, odd function)에 대한 푸리에 급수(Fourier series)이다. 간단하게 푸리에 사인 급수(Fourier sine series)라고도 한다.
 (1)
(1)
여기서 $f(t)$는 기함수라 가정했고, $T$는 신호의 주기(period), $F_m$은 푸리에 계수(Fourier coefficient)이다. 푸리에 급수는 임의의 주기 함수(periodic function)를 삼각 함수(trigonometric function)의 무한 급수(infinite series)로 표현할 수 있어서 매우 신기하다. 경이로운 푸리에 급수를 이용해서 일반 함수의 특성을 기저 함수의 무한 급수로 분석하는 방법은 푸리에 해석(Fourier analysis)이라고 부른다. 식 (1)이 성립하기 때문에, 푸리에 계수 $F_m$은 다음과 같은 적분을 통해 쉽게 구할 수 있다.
 (2)
(2)
여기서 $F_{-m}$ = $-F_m$, 첫째식은 어떤 함수 $(\cdot)$를 한 주기 $T$에 대해 적분(integration)이다. 기함수를 한 주기에 대해 적분하면 둘째식에 있는 사인 함수(sine function)의 직교성(orthogonality: 서로 다른 두 함수를 곱해 적분하면 항상 0이 되는 성질)에 의해 셋째식이 얻어진다. 유명한 식 (2)는 푸리에Joseph Fourier(1768–1830)가 제안한 푸리에 계수를 결정하는 방법이다. 만약 $f(t)$가 우함수이면 식 (2)의 마지막 적분식에 의해 $F_m$ = $0$이 된다. 즉, 식 (2)의 적분식은 우함수와는 관계없는 식이다. 혹은 식 (2)의 적분식은 어떤 함수의 기함수 특성을 뽑는 식이라 생각할 수도 있다.[∵ 우함수 특성은 0이 되기 때문에]
여기까지는 왠만한 통신 이론 책에 나오는 내용이라 특별한 부분은 없다. 하지만 푸리에 급수를 식 (2)에 있는 적분으로 외우고 푸리에 급수의 모든 면을 다 안다고 생각하면 큰 오산이다. 푸리에 급수의 핵심은 식 (2)가 아니고 식 (1)이기 때문이다. 식 (1)이 성립하면 식 (2)는 자동적으로 얻어진다. 통신 이론을 배운 대부분의 학생들은 식 (1)을 고민하지 않는다. 식 (1)을 푸리에 급수의 정의라 생각하고 교수가 하는 말을 그대로 받아들이는 경우가 99.9%이다. 하지만 이런 학생들은 현재를 넘어서는 새로운 통신 방식을 제안할 수 없다. 식 (1)의 의미를 심각하게 고민하고 교수말을 믿지 않는 고집스러운 0.1%의 학생들이 장래에 진정한 통신공학자가 될 것이다. 푸리에 급수를 고민하지 않고는 CDMA(Code Division Multiple Access), OFDM(Orthogonal Frequency-Division Multiplexing), MIMO(Multiple-Input and Multiple-Output)와 같은 창의적인 통신 방식을 제안할 수 없다. 통신에서 푸리에 급수를 사용하는 이유는 무엇일까? 바로 신호 처리가 쉽기 때문이다. 식 (1)로 다시 돌아가 상상한다. 주기 함수 $f(t)$를 그대로 사용하기가 쉬운가 아니면 삼각 함수의 무한 급수를 사용하기가 쉬운가? 언뜻 보면 무한 급수가 없는 $f(t)$를 쓰기가 쉬울 것 같지만 우리는 주기 함수 $f(t)$에 대해 아는 부분이 없어 이 함수를 그대로 쓸 수는 없다. 하지만 푸리에 급수로 통칭하는 삼각 함수의 무한 급수는 계수 $F_m$만 결정되지 않았고 시간적 변화를 의미하는 삼각 함수는 모두 결정되어 있으므로 주기 함수 $f(t)$의 성질을 푸리에 급수를 이용해 분석할 수 있다. 따라서 시간적으로 변하는 $f(t)$를 푸리에 계수 $F_m$만으로 결정할 수 있다. 이 뜻을 제대로 이해하기가 통신 공부의 시작이다.
식 (1)은 증명이 필요한 공식이다. 푸리에가 이 방법론을 제안했을 때 가장 많은 비판을 받은 부분이 식 (1)이다. 식 (1)은 절대 정의가 아니다. 식 (1)이 푸리에 급수의 정의라면 이후 전개되는 식 (2)와 같은 내용은 동어반복이 되어 수학 이론에 심각한 결함이 된다. 대부분의 경우 식 (1)은 맞지만 모든 경우에 대해 성립하지는 않는다. 이 개념을 이해하기 위해 [그림 1]을 본다. 삼각 함수를 계속 더해가면 [그림 1]처럼 톱니파(sawtooth wave)를 근사화할 수 있다. 무한개의 삼각 함수를 더하면 톱니파를 완벽히 표현할 수 있다. 그런데 문제점이 하나 있다. $t$ = $\pm \pi, \pm 3 \pi$ 등에서 톱니파는 불연속이어서 함수값을 특정할 수 없다. 그런데 푸리에 급수는 불연속점인 $t$ = $\pm \pi, \pm 3 \pi$ 등에서 함수값이 0이라고 하고 있다. 그래서, 불연속 함수(discontinuous function) 측면으로 보면 푸리에 급수는 식 (1)을 항상 만족하지는 않는다. 따라서, 식 (1)의 등호(=)를 새롭게 바꾸어서 불연속 함수에도 적용가능하도록 해야한다.[∵ 불연속인 경우는 등호가 성립하지 않기 때문에 식 (1)을 다르게 써야 한다.] 식 (1)의 증명을 위해 푸리에 급수를 확장한다. 기함수와 전혀 다른 특성을 갖는 우함수(偶函數, even function)에 대해 푸리에 급수를 정의하면 다음과 같다. 우함수에 대한 푸리에 급수는 푸리에 코사인 급수(Fourier cosine series)라고 한다.
 (3)
(3)
식 (2)와 동일한 방법을 식 (3)에 적용하면 계수 $G_m$을 다음처럼 얻을 수 있다.
 (4a)
(4a)
여기서 $G_{-m}$ = $G_m$이다. 노이만 수(Neumann number) $\varepsilon_m$을 이용해 식 (4)에 등장한 적분을 더 편하게 표현할 수 있다.
 (4b)
(4b)여기서 $\varepsilon_m$ = $2 - \delta_{m0}$, $\delta_{ml}$은 크로네커 델타(Kronecker delta)이다. 따라서 푸리에 급수는 기함수, 우함수 여부에 따라 사인(sine) 혹은 코사인(cosine) 함수로 표현할 수 있다. 만약 $g(t)$가 기함수이면 식 (4)의 마지막 적분식에 의해 $G_m$ = $0$이 된다. 즉, 식 (4)의 적분식은 기함수와는 관계없는 식이다. 다른 측면으로 보면 식 (4)의 적분식은 어떤 함수의 우함수 특성을 추출한다.[∵ 기함수 특성은 0이 되기 때문에] 또한, 다음처럼 모든 함수는 우함수와 기함수의 합으로 표현할 수 있다.
 (5)
(5)
따라서, 식 (1)과 (3)을 합치면 우함수와 기함수 특성이 모두 합쳐지기 때문에 임의의 주기 함수에 대한 복소 푸리에 급수(complex Fourier series)를 얻을 수 있다. 복소 푸리에 급수는 기함수 혹은 우함수 여부에 관계없이 모든 주기 함수에 적용할 수 있는 일반적인 기법이다.
 (6)
(6)
식 (6)을 정리하면 다음과 같다.
 (7)
(7)
여기서 $F_{-m}$ = $-F_m$, $G_{-m}$ = $G_m$이다. 식 (2)와 (4)를 일반 함수 $h(t)$에 적용하기 위해 식 (5)처럼 $h(t)$ = $h_{\rm even}(t) + h_{\rm odd}(t)$라 한다. 다음으로 식 (2)와 (4)의 최종 결과인 $F_m$, $G_m$ 표현식을 식 (7)에 대입하면 복소 푸리에 계수 $H_m$은 다음으로 결정된다.

 (8)
(8)
혹은 식 (7)의 최종 결과인 $h(t)$ = $\sum_{m=-\infty}^\infty H_m e^{i m \omega_0 t}$를 $-T/2$에서 $T/2$까지 직접 적분해서[혹은 복소 지수 함수의 직교성을 이용해서] 식 (8)을 구할 수 있다. 푸리에 급수 개념을 정리하기 위해 복소 푸리에 급수와 푸리에 사인 및 코사인 급수의 관계를 증명한 식 (5)에서 (8)까지를 다시 본다. 우함수와 기함수 특성을 차례로 합치면 일반식인 복소 푸리에 급수가 식 (7)과 (8)처럼 얻어진다. 거꾸로 복소 푸리에 급수로부터 푸리에 사인 및 코사인 급수를 유도하려면 복소 지수 함수(complex exponential function)를 오일러 공식(Euler's formula)을 이용해 코사인과 사인으로 분해하여 식 (8)처럼 적분한다. 그러면 복소 푸리에 급수의 계수 $H_m$이 $F_m$과 $G_m$으로 나누어짐을 보일 수 있다. 푸리에 계수의 수렴 특성을 알기 위해 다음 적분식을 생각한다[1].
 (9)
(9) (10)
(10)
만약 $f(t)$가 제곱 적분 가능한 함수(square-integrable function)이면 식 (10)의 좌변이 유계(bounded)가 된다. 또한 정수 $M$은 한없이 커질 수 있으므로 식 (10)의 좌변이 무한 급수가 되더라도 유계가 된다. 따라서, $f(t)$가 제곱해서 적분 가능한 경우 푸리에 계수 제곱값의 무한 급수는 항상 수렴한다.
[그림 2] 디리클레 핵심의 함수값(출처: wikipedia.org)
푸리에 급수가 원래 함수로 수렴한다는 증명은 다음의 등비 급수(geometric series)부터 시작한다.
 (11)
(11)
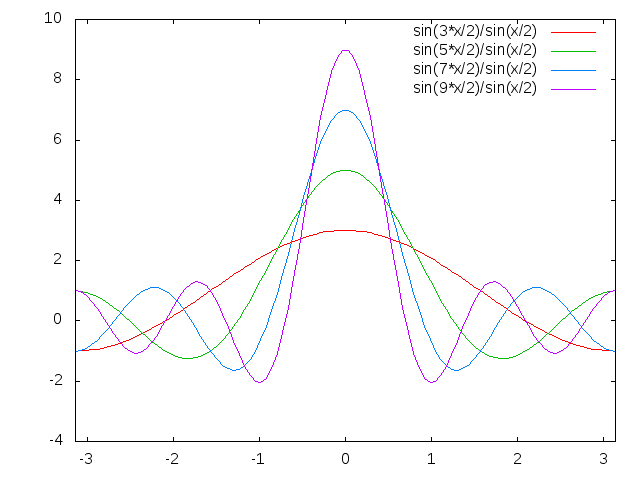
식 (11)의 우변에 있는 등비 급수(geometric series)는 매우 중요하기 때문에 특별한 이름이 붙어있다. 푸리에 급수가 가진 원래 함수로의 수렴성을 증명한 디리클레Peter Gustav Lejeune Dirichlet(1805–1859)의 이름을 따서 다음 등비 급수를 디리클레 핵심(Dirichlet kernel)이라 부른다.
 (12)
(12)
디리클레 핵심은 등비 급수를 이용해 다음처럼 쉽게 계산할 수 있다.
 (13)
(13)
등비 급수에 사용하는 복소 지수 함수 $e^{imt}$의 개수에 집중해서 디리클레 핵심을 $D_M(t)$가 아닌 $D_{2M+1}(t)$로 표기하기도 한다. 식 (12)의 디리클레 핵심을 이용해 식 (11)의 부분 합 $S_M$을 다시 정의하면 다음과 같다.
 (14)
(14)
아래에서 푸리에 급수의 원래 함수 수렴성을 편하게 증명하기 위해 주기 $T$ = $2 \pi$로 가정한다. 이렇게 하더라도 일반성이 떨어지지 않는다.
[연속 함수와 푸리에 급수]
함수 $f(t)$가 연속이면 $f(t)$에 대해 다음 푸리에 급수 관계가 반드시 성립한다.
 (15)
(15)[증명: 디리클레 방법] [4]
디리클레 핵심을 한 주기에 대해 적분하면 다음을 얻을 수 있다.
 (16)
(16)여기서 $u$ = $-t'$이다. 식 (9)처럼 함수 $f(t)$와 부분 합 $S_M$을 서로 빼본다. 이때 부분 합은 식 (14)처럼 정의하고 함수 $f(t)$도 적분으로 바꾸기 위해 식 (16)의 둘째식을 사용한다[1]. 그러면 함수 $f(t)$와 부분 합 $S_M$의 차이는 다음처럼 함수 $f(t)$를 부분 합 $S_M$으로 근사한 경우의 오차값이 된다.
 (17)
(17)
다음으로 $M$을 무한대로 보내서 식 (17)의 결과가 0이 되면 증명은 끝이 난다. 하지만 이렇게 하기 전에 식 (17)에 나타난 함수 $f(t)$로 이루어진 식을 $g(t)$로 정의해서 그 특성을 좀더 세밀하게 파악한다. $f(t)$가 연속이기 때문에 $t \ne t'$인 경우는 $g(t)$도 연속이다. $t$ = $t'$이면 로피탈의 규칙(L'Hôpital's rule)을 통해 다음을 얻는다.
 (18)
(18)
함수 $f(t)$가 연속이면 그 미분은 유한하므로 식 (18)의 값은 존재하며 유한하다.[∵ $0 < |t-t'| < \delta \Rightarrow |[f(t) - f(t')]/\epsilon| < 1$, 여기서 $f(t)$는 유한한 점에서만 미분 불가능일 수 있으며, $\epsilon$이 매우 작은 경우 $\delta, \epsilon$은 일대일 대응이 성립한다. 이 부분이 헷갈리면 테일러 급수(Taylor series)를 봐라.] 그래서, $g(t)$는 모든 점에서 유한하다. 이 결과를 이용해 $M$을 무한대로 보내면 다음이 성립해서 식 (15)가 증명된다.
 (19)
(19)
함수 $g(t)$가 유한한 경우 식 (19)가 성립하는 이유는 [그림 3]의 사인 함수 진동으로 설명할 수 있다.

[그림 3] 진동하는 함수의 특성(출처: wikipedia.org)
$M$이 커짐에 따라 식 (19)의 사인 함수가 빠르게 진동하므로 느리게 변하는 함수 $g(t)$가 한 번은 더해지고 한 번은 빼지므로 이를 모두 모으면[혹은 적분하면] 0으로 수렴하게 된다.
______________________________
위 증명에서 함수가 연속이면 유한한 점을 제외하고 그 미분은 유한하다는 명제를 사용한다. 이 명제는 모든 경우에 대해 참일까? 아니다. 이 부분을 규명한 바이어슈트라스Karl Weierstrass(1815–1897)의 증명으로 연속성과 미분 가능성에 대한 이해가 깊어졌다. 바이어슈트라스는 삼각 함수 급수를 이용해서 모든 점에서 연속이지만 미분의 발산으로 인해 모든 점에서 미분 불가능한 함수[2]인 바이어슈트라스 함수(Weierstrass function)를 제안했다. 연속이지만 모든 영역에서 미분 불가능한 바이어슈트라스 함수는 현실과 동떨어져 있다고 생각할 수도 있다. 하지만 바이어슈트라스 함수의 대표적인 예가 프랙탈(fractal)임을 고려하면, 연속인 미분 불가능 함수(continuous non-differentiable function)는 현실에서도 중요한 의미가 있을 수 있다. 그래서 연속이지만 프랙탈과 같은 성질을 갖는 함수는 제외해야 하므로, 위와 같은 방식으로 증명할 때는 매우 조심스럽게 접근해야 한다.
[증명: 스튀름–리우빌 이론(Sturm–Liouville theory)]
스튀름–리우빌 이론을 이용하면 쉽게 식 (15)를 증명할 수 있다. 먼저 푸리에 급수가 식 (20)에 있는 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)을 만족함을 보인다.
 (20)
(20)다음 단계로 $p(x)$ = $1$, $q(x)$ = $0$, $r(x)$ = $1$, $\lambda$ = $m^2$을 식 (20)에 대입한다.
 (21)
(21)
즉, 복소 지수 함수는 스튀름–리우빌 미분 방정식을 만족하며 경계 조건이 주기적이므로 경계 조건이 고정되었다. 따라서, 복소 지수 함수는 고유 함수의 완비성(completeness of eigenfunctions)을 만족하여 모든 함수를 식 (15)처럼 표현할 수 있다.
______________________________
식 (19) 증명은 [그림 3]을 이용해서 대충하면 되지만 이런 정도 설명에 만족하면 진전은 별로 없다. 우리가 헷갈리는 개념은 수학의 대가들도 헷갈린다. 전문가도 실수할 수 있는 부분이라서, 우리 수양의 부족보다 그 헷갈림 속에 명확하게 설명되지 않는 수학적 진리가 있기 때문이다. 식 (19)를 명확히 증명하려면 리만–르베그 보조 정리Riemann–-Lebesgue lemma)를 이용해야 한다. 리만–르베그 보조 정리를 증명하려면 적분법의 진정한 의미를 고민해야 된다. 푸리에 급수를 연구하던 리만Bernhard Riemann(1826–1866)이 리만 적분(Riemann integral)을 새롭게 정의하고 삼각 함수 급수의 유일성을 고민하던 칸토르Georg Cantor(1845–1918)가 집합론(set theory)을 제안했던 사실은 우연이 아니다. 수학 역사에서 보면 푸리에 급수는 새로운 신천지였다. 푸리에 급수로 인해 함수(function)의 개념, 연속성과 미분 가능성, 무한 급수, 적분법, 집합론 등이 변화되었거나 새롭게 제안되었다. 푸리에는 열 방정식(heat equation)을 풀기 위한 해법으로 푸리에 급수(Fourier series)를 제안했다[6]. 열은 물리적인 실체를 가지며 측정도 가능하기 때문에 푸리에 급수가 적절한 해법임은 분명했다. 하지만 수학적으로는 결함이 있었다. 불연속 함수를 삼각 함수의 합으로 표현할 수 있다는 관찰은 푸리에 급수의 큰 문제점이었다. 푸리에 급수는 수학자 라그랑주Joseph-Louis Lagrange(1736–1813)의 사랑하는 제자 푸리에가 제안한 획기적인 방법이었지만, 수학적으로 결함이 있는 방법을 라그랑주는 절대 인정할 수가 없었다. 19세기 초반에는 불연속 함수를 함수로 취급하지 않았기 때문에 불연속 함수를 연속 함수가 될 수 있게 하는 식 (1)은 큰 결함이라 생각했다. 요즘은 이 부분이 전혀 문제가 되지 않는다. 불연속 함수도 정의상 함수이기 때문에 이 함수를 푸리에 급수로 표현해도 수학적으로 전혀 문제가 되지 않는다. 개념을 좀더 확장하면 [그림 1]처럼 유한한 점에서 불연속인 함수도 푸리에 급수 전개가 가능하다. 디리클레가 1829년디리클레 24세, 조선 순조 시절에 증명했던 방법[4]을 참고해서 불연속점에서의 수렴 특성을 증명한다.
[조각마다 연속인 함수와 푸리에 급수]
함수 $f(t)$가 조각마다 연속(piecewise continuous)이면 다음 푸리에 급수가 반드시 성립한다.
 (22)
(22)[증명]
조각마다 연속은 함수가 유계이면서 유한한 점에서만 불연속임을 뜻한다. 식 (14)의 적분 변수를 바꾸면[$t-t' \rightarrow t'$] 다음을 쉽게 얻을 수 있다.
 (23)
(23)
식 (23)의 첫째식과 둘째식은 $t' \leftrightarrow -t'$ 변수 치환 관계를 가진다. 식 (17)처럼 주기 함수와 부분 합을 빼주면 다음과 같다.
 (24)
(24)
함수 $f(t)$로 이루어진 식을 $g(t)$로 정의해서 그 특성을 본다.
 (25)
(25)
함수 $g(t)$는 $t'$ = $0$일 때만 문제가 있으므로, 이 경우의 극한을 구한다. 변수 $t'$가 항상 0보다 크면서 0으로 접근하면 식 (25)의 첫째식을 써서 계산하면 된다.
 (26)
(26)변수 $t'$가 0보다 작으면서 0으로 접근할 때는 식 (25)의 둘째식을 쓰면 된다. 따라서, $g(t)$는 모든 점에서 유한하므로 $M$이 커짐에 따라 식 (24)는 0으로 수렴한다.
______________________________
이상의 증명을 통해 푸리에 급수를 정확히 표현하려면 식 (15)가 아닌 식 (22)를 써야한다. 또한 식 (22)에 의해 식 (9)의 베셀 부등식은 항등식이 된다. 이 항등식은 파르세발의 정리(Parseval's theorem)라고 부른다.
 (27)
(27)만약 계수 $F_m$의 제곱이 아닌 $F_m$이 절대 수렴하면, 푸리에 급수는 모든 영역에서 균등 수렴한다. 푸리에 급수의 균등 수렴성은 바이어슈트라스 $M$판정(Weierstrass $M$-test)으로 손쉽게 결정한다. 디랙 델타 함수(Dirac delta function)를 이용하면 디리클레 핵심이 만드는 무한 급수를 아름답게 정의할 수도 있다. 대신 아래 식이 성립하려면, 적분 개념에 기반을 둔 리만–르베그 보조 정리가 필수적으로 적용되어야 한다.
 (28)
(28)
여기서 첫째 줄은 식 (15)에서 증명한 내용을 디리클레 핵심으로 다시 쓴 식이며 둘째 줄은 첫째 줄의 표현을 디랙 델타 함수로 다시 표기한 식이다. 물론 푸리에 급수의 완비성(completeness of Fourier series)이 성립하기 때문에 디랙 델타 함수를 식 (8)에 바로 대입해서 계산해도 식 (28)의 둘째 줄을 얻을 수 있다. 식 (28)을 다음처럼 정리하면, 충격 열(impulse train) 혹은 디랙 빗(Dirac comb)을 복소 지수 함수의 무한 급수로 나타낼 수 있다.
 (29)
(29)
[그림 4] 여러 가지 주기 함수(출처: wikipedia.org)
푸리에 급수 개념을 이용하면, 여러 초등 함수와 무한 급수의 관계를 쉽게 증명할 수 있다. 무한 급수에 대한 증명이 쉬워지는 이유는 푸리에 급수의 완비성 때문이다.
1. 급수 표현식(series representation)
[초등 함수의 급수]
 (1.1)
(1.1)
 (1.2)
(1.2)
식 (1.1)에 있는 $x$에 $x + \pi$를 대입하면 된다.
 (1.3)
(1.3)
로그 함수 $-\log(1-x)$에 대한 테일러 급수(Taylor series)를 이용해서 식 (1.3)을 증명한다.
- 톱니파(sawtooth wave)
[그림 1, 4]에 있는 톱니파를 식 (1)을 이용해 적분하면 다음을 얻는다.
 (1.4)
(1.4)
점 $x$ = $\pm \pi$ 근방에서는 불연속이며, $x$ = $\pm \pi$에서 식 (1.4)에 있는 무한 급수의 수렴값은 0이다.
- 역톱니파(reverse sawtooth wave)
[그림 1, 4]에 있는 톱니파의 좌우를 뒤집으면 역톱니파가 된다. 식 (1.4)에서 $x$ 대신 $x-\pi$를 대입하면 다음을 얻을 수 있다.
 (1.5)
(1.5)
식 (1.5)는 식 (1.3)에 제시한 무한 급수의 허수부를 선택해서 다음처럼 초등적으로 증명할 수도 있다.
 (1.6)
(1.6)
점 $x$ = $0^+$ 근처에서는 식 (1.5)의 우변이 0보다 크므로, 식 (1.6)에서 $+\pi$를 택하면 식 (1.5)의 좌변을 얻을 수 있다.
- 절대값 $|x|$
실수 $x$의 절대값에 대한 푸리에 급수는 다음과 같다.
 (1.7)
(1.7)
[그림 5] 부호 함수의 모양(출처: wikipedia.org)
- 부호 함수(sign function) $\operatorname{sgn}(x)$
[그림 5]에 있는 부호 함수의 푸리에 급수는 식 (1.7)을 미분해서 쉽게 구할 수 있다.
 (1.8)
(1.8)
여기서 부호 함수는 $x$ = $0$에서 불연속이다.
- 2차 함수(quadratic function)
2차 함수에 대해 푸리에 급수를 적용하면 다음 무한 급수를 얻을 수 있다.
 (1.9)
(1.9)식 (1.9)를 미분해서 식 (1.5)를 다시 유도할 수도 있다. 식 (1.9)에서 $x$ = $0$을 대입하면, 유명한 바젤 문제(Basel problem)의 답을 쉽게 구할 수 있다.
 (1.10)
(1.10)- 분수 복소 지수 함수(fractional complex exponential function) [5]
 (1.11)
(1.11)[참고문헌]
[1] D. Jackson, "The convergence of Fourier series," The American Mathematical Monthly, vol. 41, pp. 67–84, Feb. 1934.
[2] J. Thim, Continuous Nowhere Differentiable Functions, Master Thesis, Luleå University of Technology, Sweden, 2003.
[3] 최인혁, "해석학하는 만화 [1]: 두 번 미분하기", HORIZON, 2019년 6월. (방문일 2019-10-01)
[3] 최인혁, "해석학하는 만화 [1]: 두 번 미분하기", HORIZON, 2019년 6월. (방문일 2019-10-01)
[4] P. G. L. Dirichlet, "Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données (On the convergence of trigonometric series which serve to represent an arbitrary function between given limits)," Journal für die reine und angewandte Mathematik (Journal for Pure and Applied Mathematics), vol. 4, pp. 157–169, 1829.
[5] M. V. Berry, "Optical vortices evolving from helicoidal integer and fractional phase steps," J. Opt. A: Pure Appl. Opt., vol. 6, no. 2, pp. 259–268, Jan. 2004.
[6] 이정오, "무한급수의 총합 가능성과 후세인 보르에 관하여", 한국수학사학회지, 제30권, 제6호, pp. 353–365, 2017년 12월.
[7] 박원우, 딥러닝을 위한 푸리에 영상처리, 홍릉, 2023.
[다음 읽을거리]
1. 푸리에 변환
2. 리만–르베그 보조 정리
저.. 제가 통신을처음배워서 잘모르는데..
답글삭제식 1번과 2번을보는데 이해가 안되서요 ㅜㅜ..
식 1번은 그,..m=1부터 무한데까지 그 식이요..에프티를 주파수 f를 기함수로 풀어놓은식인가요...?
그리구 식2번이..1,2,3째줄이 이해가안되서요ㅠㅠ..
첫째줄에 인테그랄 - 2분의 T 에서 2분의 T까지 라고 정한건 무슨의미인가요,,?그리구,,안에있는식은 무슨의미인가요...또,,,,사인앞에(*)은 무슨뜻이에요...??
두째줄 사인안에있는 식도 왜그런지 궁금하구,,..ㅜㅜ
셋째줄은 =표시되잇잖아요 f(t)에대한 괄호인가요 아님 Fm에 대한 괄호인가요...
근데,..셋째줄에 2분의 T인가 넷째줄은 T분의 2이네요.....
너무질문이 많았나요..ㅠㅠ 되게궁금해서..
사실 월요일날 시험보는데 여기 자료가 되게 도움이되는거같아서 책안보고 여기보고있걱든요.. 책에 자료가없어서,.ㅜㅜ
아,,,그리고 4번째줄에서 식안에 f(t)는 갑자기 왜나오는건가요..???
답글삭제아래 간단히 답해 봅니다. 본문을 약간 수정했습니다.
삭제1. 식 (1)은 f(t)가 기함수라 가정하고 푸리에 급수로 표현한 것입니다. 우함수면 식 (1)로 표현 안됩니다.
2. 식 (2)는 푸리에가 제안한 유명한 푸리에 급수 계산법입니다.
3. -T/2에서 T/2까지 적분한 것은 한 주기에 대한 적분입니다. 0에서 T까지 적분하더라도 결과는 같습니다.
4. (.)를 쓴 것은 적분 연산자를 어떤 함수 (.)에 적용한다는 뜻으로 쓴 것입니다.
5. 식 (2)의 둘째식은 삼각함수의 적분으로 증명가능합니다. 중요한 것은 이게 사인 함수의 직교성(orthogonality)이라는 것입니다. 직교성이 있어야 식 (15)의 완비성(completeness)이 성립합니다.
6. 식 (2)의 세째줄은 f(t)가 기함수라 2배를 한 것입니다.
7. 식 (2)의 세째줄은 푸리에 계수 Fm을 구하기 위해 기함수 f(t)를 한 주기 적분한 것입니다. 직교성에 의해 푸리에 계수가 사인 함수의 한 주기 적분으로 표현됩니다.
질문있습니다
답글삭제주기함수 f(t)를 삼각함수의 무한급수로 나타내게 된다면 정말 유용하고 편리한 방법일 것이라고 생각은 듭니다. 하지만 푸리에급수의 계수를 구할때 f(t)가 필요하니까 결국 다시 어려운 방법이 되는게 아닌가요?
으.. 답변 부탁드립니다 감사합니다.
관점을 조금 다르게 보십시오.
삭제식 (1)에서 Fm은 시간에 대해 상수입니다. 시간에 따라 변화하는 것은 사인 함수이므로 사인 함수만 가지고도 시간 함수 f(t)의 변화를 볼 수 있습니다. 예를 들면 f(t)의 미분은 사인 함수를 미분해 무한급수를 계산하면 그 특성을 알 수 있습니다.
아... 그렇군요 상수니까
삭제이해가 되었어요 감사합니다^^
안녕하세요 ㅎ
답글삭제질문이 있어서 글을 남깁니다 ㅎ
주기 함수에서 푸리에 급수를 사용 한다고 했는데 주기 함수일때 푸리에 변환도 가능 한가요?
예, 가능합니다. 푸리에 급수를 확장한 것이 푸리에 변환이라 주기함수도 가능합니다.
삭제주기함수에 대한 푸리에 변환은 아래에 소개되어 있습니다.
http://ghebook.blogspot.kr/2012/08/fourier-transform.html
^^ 감사합니다~
답글삭제덕분에 많은 정보를 얻고 갑니다 ㅎ
종종 막히는 부분이 있으면 글을 남겨도 될까요? ㅎ
방문 감사합니다. 댓글은 언제든 환영입니다. ^^
삭제질문 있습니다.
답글삭제함수에 위상이 포함되어있을 땐, 어떻게 전개가 되나요??
예를 들어, f(x)=sin(W0t+세타1)이라는 기본조파 함수라면,
여기서 푸리에 변환을 한다고 생각했을때,
제 생각에는 주기함수니까 푸리에 급수로도 표현할 수 있지 않을까 싶은데,
지식이 얕아 전개가 쉽지 않네요..
어떻게 생각하시나요??
원칙은 단순합니다. 식 (6)이나 (7) 공식을 증명했기 때문에 다음부터는 기계적으로 적용하면 됩니다.
삭제말씀하신 함수는 주기함수이기 때문에 푸리에 급수로 전개하는 것이 맞습니다.
삼각함수 푸리에 급수를 이용한다면 sin(ω0*t+θ0)를 삼각함수의 합차공식을 이용해 전개하면 sin 항과 cos 항을 얻을 수 있습니다.
복소지수 푸리에 급수라면 sin 함수를 오일러 공식으로 전개하여 구하면 됩니다.
아.. 느낌은 오는데,
삭제계산이 정확히 되질 않네요.
대략적으로
an = 1/T integral 0~T까지 sin(W0t)*cosnt 이 될 것 같은데 맞나요 ㅠㅠ..
답변이 늦었네요. ^^
삭제$f(x) = \sin(\omega_0 t + \theta_0)$라면 그대로 공식에 적용해야 합니다. $\theta_0$를 생략하면 안됩니다.
존경합니다 ㅎ 좋은 지식 , 좋은 글 감사합니다 ㅎ
답글삭제존경까지야... 방문 감사합니다. ^^
삭제혹시 오일러공식을 이용해 푸리에공식까지 유도하는 과정을 나타낼수 있나요?
답글삭제오일러 공식 같은 초보적인 공식으로 푸리에 급수의 완비성을 증명하기는 어렵습니다. 위에 제시한 증명이 가장 쉽습니다.
삭제혹시 오일러 공식으로만 푸리에 급수 증명이 가능하면 수학 논문지에 내시면 될겁니다.
교수님이 리포트로 오일러공식으로 푸리에공식까지 정리해야지고 내라는데 그냥 이걸 이해하면 되는건가요?ㅠㅠ
답글삭제아마 그 내용은 증명을 하라는 게 아니고 식 (2) 등을 이용해 연습하라는 의미 같네요. 열심히 연습하세요. 하지만 계산 연습은 증명이 아닙니다.
삭제(7)에서 (8) 로 어떻게 넘어가는 거죠??
답글삭제더 알기 쉽게 본문을 수정했습니다.
삭제정의한 even/odd function 들이 h(t) 와 h(-t) 의 +- 조합으로 각각 이루어져 있는데,
삭제이것이 정리 과정에서 h(t) 에 대해서 통일되는 것이 잘 이해가 안되요.
결국은 어떤 식으로 정리되던간에,
1) h(-t) => h(t) 로 바뀌는 과정이 있거나, (t->-t 치환적분)
2) h(-t) 를 포함하는 항이 evenfunction 이어서 -T/2 ~ T/2 적분시 소거가 되거나,
둘중의 하나가 필요할 것 같은데, 2)번은 h(t) 자체의 우함수/기함수 여부는 알수 없기 때문에 불가능할 것 같고, 1)번을 통해서 정리가 되어야 하지 않나 싶은데,
계산해봤는데 쉽게 치환후 정리가 되지는 않네요.
죄송한데, 저 과정을 좀더 풀어서 써주실 수는 없나요? ^^;;;;;
Fourier Series, Fourier Transfrom 을 통틀어서 저부분만 안풀리네요. 흑
식 (8) 수식과 본문을 다시 수정했습니다.
삭제푸리에 계수를 구하기 위해 사인이나 코사인을 곱해 적분하면 기함수나 우함수 특성만 뽑아집니다. 이게 중요한 푸리에 급수의 특성입니다.
저것이 문제였었군요. 모든 퍼즐이 풀렸습니다. 감사~ ㅎㅎㅎ
삭제안녕하세요. 공학수학 공부하다가 막히는 부분이 있으면 항상 선생님의 블로그부터 들려 만족할 만한 정보를 얻고 갑니다.
답글삭제오늘 푸리에급수에 관한 시험을 치뤗는데, 제가 올바른 답을 적었는지 궁금하여 여쭤봅니다.
푸리에 급수가 사인과 코사인의 무한급수 합으로 표현될 수 있는 이유에 대해 서술하라는 문제입니다.
선생님의 답변을 듣고싶습니다.
선생님 아닙니다, 익명님. ^^ 전파거북이입니다.
삭제복소 푸리에 급수는 식 (5)와 (8)을 이용해 푸리에 사인과 코사인 급수로 만들 수 있습니다. 반대도 가능하고요. 핵심은 기함수와 우함수 관계입니다.
정말...어렵네요..
답글삭제수학, 특히 해석학 분야는 푸리에 급수 이전과 이후로 나누어진다고 생각합니다. 그 정도로 영향력이 큰 부분이 푸리에 급수라서 처음 공부하면 쉽지 않습니다. 어렵게 느끼는 것이 정상입니다. ^^
삭제작성자가 댓글을 삭제했습니다.
답글삭제서로 분야가 달라서 그런지 용어도 생소하네요. "Vertical BW"라고 쓰신 것은 비디오 대역폭(video bandwidth)을 의미하나요?
삭제주파수 대역 측정기(spectrum analyzer)는 기본적으로 FFT 개념이 들어가기 때문에 주기 신호와 비주기 신호를 나눌 필요는 없을 것 같은데요.
해상도 대역폭(resolution bandwidth)를 고정하면 주어진 주파수 대역의 측정 표본수가 정해집니다. 비디오 대역폭 마저 고정하면 훑기 시간(sweep time)도 거의 정해져서 훑기 시간을 10배 키운다 해도 측정 결과가 바뀔 것 같지는 않네요. (잡음 특성은 좋아지겠지요.)
T.T 어렵네요.
답글삭제1. 식(9)가 잘 몰라 좀 찾아보니, 3째줄에 적분 전상태이므로 Σ앞에 T가 없어야 하지 않을까요?
2. 블로그 오른쪽위 검색이 예전에 됬었는데, 안되네요. T.T
또 틀렸네요. T.T
삭제곰유님 덕분에 수식 수준이 더 좋아졌습니다. 진정으로 감사드립니다. ^^
블로그 검색은 가끔씩 안됩니다. 구글이 주기적으로 갱신하면서 무언가 초기화되는 것 같습니다.
와~ 정말 어렵네요. (하긴 지금까지 쉬운것은 없었지만.ㅋㅋㅋ)
삭제거의 식 2개로 하루종일 보네요. (요즘 좀 한가해서요 ㅋㅋㅋ)
문의드릴 내요 아래 링크에 두었습니다. 부탁 드립니다.
http://blog.daum.net/share_like_bear/116
위링크에 있는 질문 리스트만 여기에 복사를 해놓았습니다.
1. 식(9) 아래와 같이 하는 것이 맞는지 좀 봐주실수 있으실런지요?
1-1.너무 기초적인 질문인데요. 식(9)관련하여 보다가 한참 해맸던 부분인데요. 처음에는 아래식의 우측방식으로 하다가 보니, 와무래도 아닌거 같아서, 아래식의 중간에 있는 것으로 하였는데요. 이게 복소수와 관련이 있는건가요? 질문이 좀 이상하지요?
2. 식(16)관련
2-1. 식(16)이 왜 있는건가요? 증명과정에서 사용하고 있지 않은거 같아서요. (아직 전체적으로 이해를 하지 못한상태에서 드리는 질문T.T)
2-2. 식 16의 첫줄은 2π Σ [sin(mπ)/mπ]이 되어 Sinc function이 m=0일때는 1이고, 그외에는 0으로 2π 되는게 맞는건가요?
2-2-1. 이렇게 우선 계산을 하면 안될거 같은게 Sinc function은 m=0일때, 분모가 0인지라 좀 사용하기 꺼림직해서요.
2-3. 둘째줄은 첫줄에서와 같은 방식으로 해보았는데, 안되네요.약간 힌트를 좀
3. 식(1)에서 m=0부터 하지 않은 이유가 있는건가요? 아님 별 의미가 없어서 인가요?
천재와 만나는 시간인데 쉬우면 이상한 것이지요. ^^
삭제1-1. 식 (9)가 틀렸었네요. 저번에 오차 지적해서 고칠 때 $T$가 아닌 $dt$를 삭제했어야 되네요. 죄송합니다.
질문하신 부분을 계산할 때 복소 지수 함수의 직교성을 사용해야 마지막 항이 증명됩니다. 링크에 제시한 것처럼 하면 증명이 되지 않습니다.
2. 식 (16)은 디리클레 핵심의 매우 중요한 성질입니다. 식 (16)을 식 (17)에 사용하고 있습니다.
2-2-1. 디리클레 핵심을 사인 함수로 보지 말고 복소 지수 함수의 합으로 보세요. 충분히 잘 정의된 함수입니다.
3. $m = 0$이면 사인 함수 때문에 항 전체가 0이 됩니다.
1. 1-1. 추후에 해보고 다시 문의드리겠습니다.
삭제(먼가 해본게 이상하다 싶어서..., 역시나 T.T)
2-2-1. 오히려 말씀하신대로 하니 계산이 더 간단하더군요.
2-3. 합을 편쳐서 하니 바로 나오데요. 왜이렇게 생각이 막혔는지, T.T 말씀하신방식으로도 해보았습니다. 역시 더 간단.
감사드립니다.
4. 식(18)에 두번째 줄에는 sine 항목 미분하여 cos 0=1 이 분모가 있는 것이지요?
4. 예, 분자와 분모를 모두 미분하는 로피탈의 정리를 이용했습니다.
삭제1. 식(9)관련하여 이번엔 재대로 한거 같긴한데요. 다시 한번 봐주실 수 있으시겠는지요?
삭제http://blog.daum.net/share_like_bear/116
처음에는 찾아본 자료들과 약간 다른 부분있어 증명이 될 수 있을까? 의심했는데, 되네요. ㅋㅋ
예, 그렇게 하시면 됩니다. ^^
삭제좀 두서 없는 질문 입니다. 헤~~~
삭제예전에 basis function이라는 것을 물어보았었는데요.
"기저 함수(basis function)는 어떤 수치 해석법을 쓰느냐에 따라 정의와 의미가 달라집니다. 일반적으로는 푸리에 급수 정도를 생각하면 됩니다."
1. 그럼 식(15)의 첫줄 식에서 e^imt가 basis가 되는건가요?
2. 그리고 EM에서는 공간에 대한 함수가 되는거구요?
두리뭉실하게 답한 이유가 있습니다. 기저 함수는 모을 경우 어떤 모양이든 전체를 설명할 수 있는 함수입니다. 하지만, 명확하게 기저 함수의 완비성이 증명된 것은 푸리에 급수 부류입니다. 스투름-리우빌 이론에서 파생된 푸리에 급수의 아류들도 여기에 해당됩니다.
삭제실제 문제에서는 경계 조건 문제로 인해 완비성이 검증된 기저 함수를 사용할 수 없습니다. 그래서 여러 가지 문제가 생기지만 현실적인 이유로 기저 함수로 정의해 사용합니다.
1. 기저 함수라 할 수 있습니다. 구체적으로는 전역 기저 함수(global basis function)라 합니다.
2. 전자파는 파동이므로 공간과 시간 모두에 대해 기저 함수를 정의할 수 있습니다.
1. 아직은 답변해 주신 내용을 모르겠습니다. T.T
삭제그냥 모르고 하는 질문입니다. 말도 안되는 질문인건 저도 아는데요.T.T
궁금해서요. 혹시나 해서요. .
1-1. 스투름-리우빌 이론에서 파생된 푸리에 급수의 아류들 중에 그린 함수가 포함이 되는건가요?
1-1-1. 어떤 MOM기반 planer-3DEM(PCB같은 평면 형태 구조만 해석)이 경계조건을 설정을 따로 하지 않아서, 어떤분이 물어 보더라구요. 이건 왜 경계조건이 없을까?
1-1-1-1. 스투름-리우빌 이론에서 파생된 푸리에 급수의 아류들은 경계조건이 없어도 해석을 할 수 있는 건가요?
2. [기초질문T.t]식(23)에서 변수를 쉽게 어떻게 바꾸는 건가요?
3. 식(19)에 대한 물리적인 의미는 설명해주신거로 알겠는데요.
S_m(t)가 f(t)의 부분합이지만,
M이 무한대가 되면, S_m(t)가 f(t)와 같아 지므로 0이 되는 것으로 증명은 할 수 없는건가요?
1. 기저 함수는 그린 함수와는 다릅니다. 푸리에 급수의 아류들은 베셀, 르장드르, 게겐바우어, 마티외 함수 등이 있습니다. 이들은 모두 완비성이 있습니다.
삭제2. $t' \rightarrow -t'$
3. 식 (19)가 증명입니다.
그리고, 미분 방정식을 경계 조건 없이 풀 수는 없습니다. MoM에서도 경계 조건이 있습니다. 사용자가 설정할 필요 없이 기본 설정을 쓰는 것이지 경계 조건이 없는 것이 아닙니다.
삭제2. 식(23)의 첫째줄에서 둘째줄로 가는게, even 함수특성이 있어서, D_m(t') = D_m(-t') 인것은 알겠는데요. 식(14)에서 식(23)의 첫줄이 어떻게 바꾸는지 아리송해서요.
삭제혹시, 단순하게
f(t') D_m(t - t')에서
t - t' = t_1 , t ' = t - t_1 로 해서
f( t - t_1 ) D_m( t_1 )
다시 t_1 ==> t' 해서
f( t - t' ) D_m( t' )
이렇게 하는건가요?
예, 맞습니다. ^^
삭제식(26)관련
삭제분모 뿐만 아니라, 분자들도
lim f(t_+) - f(t+t') = 0
t'->0_+
lim f(t_-) - f(t-t') = 0
t'->0_-
이기 때문에, 로피탈정리를 적용하는 게 아닌가요?
맞습니다.
삭제죄송합니다.재가 착각을 한거 같습니다.
삭제(0의 +에서 접근하는거)
lim f(t_+) - f(t+t') = 0
t'->0_+
(-에서 0으로 접근하는거)
lim f(t_-) - f(t-t') = 0
t'->0_+
해서 하나의 식에 +에서 접근 하는거와 -에서 접근하는것이 다 있는거 같네요.
식 (24)를 잘 보기 바랍니다. 중요한 것은 $g(t)$가 발산하지 않는다는 것입니다.
삭제증명에서 로피탈의 정리를 사용하기는 하였지만,
삭제연속 불연속 무관하게, 함수가 주기적이기만 하면, 결국 불연속이 나올거 같으면, 로피탈정리를 사용하면 되는거다. 이렇게 봐도 무리가 없는건가요?
조금 다른 것 같습니다. 로피탈 정리가 적용되는 영역(or 근방)에서는 함수가 연속이 되어야 합니다. 함수 $f(t)$를 교묘하게 변형해서 $g(t)$가 되게 하면서 로피탈 정리를 항별로 각각 적용해 발산되지 않게 하는 것이 디리클레가 제안한 증명의 핵심입니다.
삭제1. 그럼 주가함수 f(t)에 부분함을 빼는 이유는 교묘하게 변형하여 g(t)를 만들기 위한 과정인건가요?
삭제2. 그런데 g(t)가 수렴을 하면 왜 프리에 급수가 성립을 하는 것인가요?
2-1. 엄밀하게는 프리에 급수가 함수라는 것을 증명하는 건가요?
1. 예, 발산하지 않는 $g(t)$를 만들기 위한 것입니다.
삭제2. $g(t)$가 수렴하는 것이 아니고 전체 적분값이 0으로 갑니다. 이 부분을 증명하려면 리만-르베그 보조 정리를 봐야 합니다. 아래 참고하세요.
http://ghebook.blogspot.kr/2012/08/riemann-lebesgue-lemma.html
아 질문이 너무 깊이 들어 가지 않은가 싶습니다. 추후에 기억도 못할 것 같은뎅~~ T.T
삭제2. 식(15)와 (22)는 프리에 급수의 수렴성을 증명한건가요?
2-1. 현대에 불연속 함수도 함수로 분류한다면, 식(22)를 식(15)와 같이 표현에도 무관한거 아닌가요?
3. 약간 헷갈리는 부분인데요. g(t)무관하게 M이 커지면, 0으로 수렴하는거 아닌가요?
2. 맞습니다.
삭제2-1. 식 (15)는 연속 함수에 대한 증명, 식 (22)는 유한점 불연속 함수에 대한 증명입니다. 서로 다른 증명입니다. 물론 식 (22) 증명은 식 (15)를 포함합니다.
3. 리만-르베그 보조 정리가 성립하려면 $g(t)$가 유한해야 합니다.
시간에따라 주파수가 변할경우 푸리에 변환이 되는가요?
답글삭제비선형이 되기 때문에 일반적인 푸리에 변환으로는 답을 찾을 수 없습니다.
삭제이 부분은 회로 설계에서도 중요한 부분이서 학문 분야가 따로 있습니다. 간단히는 "조화 해석(harmonic analysis)", 더 구체적으로는 "비선형 조화 해석(nonlinear harmonic analysis)"으로 부립니다. 이 분야에서는 비선형을 다루기 때문에 시간에 따라 주파수가 변동하는 것도 이론적으로 처리 가능합니다만 실험을 해보면 괴리는 있습니다. 고출력으로 가면 이론과 실험의 차이는 더 커지고요.
제가 지금 푸리에를 해야하는 식이 하나 있는데 잘 안풀려서 질문을 드리고 싶습니다.
삭제E field = exp(j w1 t) + exp(j w2 t)
w1 =w1(t)=w0 + delta w * cos(cost + phi)
일때,
F{E * conj of E} = ?
이것 입니다...
위식에서 w2, delta w, w0 등은 상수이며
답글삭제일단 w1만 시간 t에따라 바뀝니다.
적분표를 보시고 답을 찾는게 빠를 것 같습니다. 푸리에 변환이 문제가 아니고 적분이 문제입니다. 아래 수학 공식책 참고하세요.
삭제http://ghebook.blogspot.kr/2010/09/blog-post.html
식(28) 증명관련하여, 해결이 될듯해서 문의댓글을 삭제하였는데, 아~ 다시 모르겠네요. 힌트좀...헤~
답글삭제1. 첫줄을 증명하려면, f(t')가 f(t)가 되어야 할거 같은데, 그럼 둘째줄이 증명이 되어야 가능하거 같은데요.
1-1. 둘째줄이 디리클레 핵심을 적분 하면 2pi, 즉 2pi·1
여기에서 1은 디렉텔타함수를 적분한거로 증명이 되는 건가요?
1-1-1. 그런데 디렉 델타함수 안에 2npi는 어떻게 들어가게 되는 건가요?
1-2. 적분하지 않고, 둘째줄을 증명을 할수 있나요?
2. 둘째줄없이 첫줄을 증명할 수 있나요?
푸리에 급수가 증명되었기 때문에 델타 함수를 적분해서 푸리에 계수를 구하면 쉽게 식 (28)이 증명됩니다.
삭제식 (28)의 첫째줄은 푸리에 급수의 증명이고 둘째줄은 증명을 활용해 델타 함수의 푸리에 급수를 구한 식입니다.
델타 함수 안의 $2n \pi$는 주기 함수이기 때문에 들어간 것입니다.
식(28)첫줄은 어째어째 했는데, 둘째 줄은 T.T
삭제아래 링크 문의드릴 내용 두었습니다.
http://blog.daum.net/share_like_bear/116
위 링크에 질문 목록만 아래에 복사해 두었습니다.
----------------------------------------------------------
1. 식(28) 첫줄 증명을 해보니, 프리에 급수의 그냥 다른 형태 같은데요.
맞는지좀 한번 봐주실수 있으시겠는지요?
1-1. 좀 찜찜한게, 계수 Fm에는 f(t')가 있는데, 최종 결과를 f(t)라고 해도 상관 없는건가요?
1-2. t'가 무엇을 정의하기 위한 가요? 또다른 임의의 변수를 정의 하기 위한건가요?
2. 식(28)둘째줄을 아래까지는 해보았는데, 시그마가 최종적으로 없어지지가 않는데요.
힌트좀...
2-1.리만-리베그 보조 정리가 sin, cos, 지수함수 이외에도 디렉델타 함수에서도 적용이 되는 건가요?
식 (28)의 둘째줄은 보통의 푸리에 급수책 보면 델타 함수 정의를 이용한 연습 문제 정도로 나옵니다. 적분할 필요도 없습니다.
삭제식 (28)의 첫째줄은 푸리에 급수의 완비성 증명입니다. 푸리에 계수를 구하는 것과 푸리에 급수의 완비성 증명은 차원이 다릅니다.
1-1. 델타 함수를 보시면 쉽게 이해될 것입니다. 같은 점이라 같습니다.
2-1. 리만-르베그 보조 정리가 델타 함수에 적용되는 것이 아닙니다. 델타 함수는 일종의 표기법입니다.
T.T
삭제1. 식(28 둘째줄을 증명하기 위해서, f(t')=δ(t−t')로하고 첫줄에 입력하면 증명이 되는건가요?
2. 식(28 둘째줄의
δ(2nπ+x−x') when n= 0, ±1, +2....
은
... + δ(-2nπ+x−x') + ...+ δ(-2π+x−x')+δ(x−x')+ δ(-2π+x−x')+...+ δ(2nπ+x−x') + ...
와 같은 건가요?
2-1. 아님
... + δ(-2nπ+x−x') + ...+ δ(-2π+x−x')+δ(x−x')+ δ(-2π+x−x')+...+ δ(2nπ+x−x') + ...
중에 하나 인건가요?
위에도 설명했듯이 $2n\pi$는 주기 함수를 만들기 위한 조건이니 적분할 때는 신경쓸 필요 없습니다.
삭제델타 함수를 식 (8)의 마지막식에 넣으면 식 (28)의 둘째줄을 증명할 수 있습니다.
감이 좀 잡히긴 한데, 좀더 생각을 해봐야 겠습니다.
삭제그리고 프리에 급수를 처음에는 깊이 들어 갈 생각이 없었는데,
보면 볼수록 오묘하고, 생각하면 생각할 수록 가능성 등이 무한할거 같다는 생각이 듭니다.
물론 재가 이걸 실무에 적용할 수 있을 정도로 깨달음을 얻을 수 있을지는 미지수 이지만요. T.T
1. 둘째줄의 증명은 적분해서 같다는 것을 보인다는 것은 적분식 안에 있는 것이 같다는 것을 증명할 수 있는 것은 아닌듯 합니다. 그리고 n을 m으로 표기한 것도 그렇구요. 맞나요?
2. f(t')=δ(t−t') 만 적용하여 증명이 된다고 말한다는 것은 일반성이 떨어지기 때문이지요?
3. 식(28)첫줄을 증명을 하다가 보니, 식(28)첫줄 증명과 무관한게, 약간 햇갈리는 부분이
식(17)함수 주기함수f(t)와 부분합 S_M(t) 인데, 좀 이상하게 보입니다.
즉 식(15)를 기준으로 보면,
f(t)는 m이 (-)무한대에서 (+)무한대 이고,
S_M(t)의 m은 -M에서 +M인데, 어떻게 식(17)의 둘째 줄과 같이 정의가 될수 있는가 입니다.
1. $n,m$은 별개의 서로 다른 지표입니다.
삭제2. 델타 함수는 함수라기보다는 정의이기 때문에 그렇습니다.
3. $M$이 무한대로 가기 때문에 동일합니다. 물론 수렴성은 따져야 합니다.
3. 식(11)에서 주기함수 f(t)의 부분합 S_M(t) 이 디리클레 핵심의 m은 -M에서 +M이고,
삭제주기함수 f(t)의 디리클레핵심의 m은 (-)무한대에서 (+)무한대 인데,
식(17)에서의 m은 -M에서 +M인 디리클레 핵심의 범위는 묶여 있는 이게 어떻게 가능한가요?
위에 이미 답이 되었습니다. $M$이 고정된 것이 아니고 계속 커집니다, 무한대까지. ^^
삭제음~ 아 생각이 한번 고정되니 무엇을 잘못 생각하고 있느지 모르겠습니다. T.T
삭제식(19)에서 부분합 S_M(t) 이 디리클레 핵심의 m은 -M에서 +M을 M을 무한대로 극한하니깐 f(t)와 같아 지는데요.
식(17)은 주기함수 f(t)의 부분합 S_M(t) 이 디리클레 핵심의 m은 -M에서 +M.
식 (17)에서 증명이 끝나는 게 아니고 식 (19)까지 이어집니다. 다시 잘 보세요. ^^
삭제안녕하세요, 일전에 질문 드렸던 전자과 학생입니다.
답글삭제푸리에를 왜 하는지에 대해서 설명을 해주실때, 푸리에 계수를 알면
time domain의 원신호를 삼각함수의 합으로 표현이 가능하다고 하였습니다.
그러나 푸리에 시리즈를 하다보면, 그래프로 나타낼때
x축은 frequency, y축은 X(f)의 magnitude로 많이 표현을 하는데요
가령, 700MHz에서 X(f)가 가장 크게 나오고, 100MHz에서 X(f)가 그다음으로크게 나오고.....
를 해석하면, time domain에서의 신호는 700MHz를 가장 많이 포함하고 있고, 100MHz를 그다음.... 으로 포함하고 있다.
라고 해석하라고 합니다.
어째서 단순히 푸리에 계수로 그런 판단을 할 수 있는지 이해가 안됩니다.
직관이지 않기 때문에 어렵습니다. 식 (22)가 푸리에 급수의 핵심입니다. 분명히 시간 영역과 주파수 영역이 등호(=) 관계입니다.
삭제단순히 보면 모든 임의의 신호는 주파수를 가진 주기 신호의 합이 된다는 것이 푸리에의 주장입니다. 이 부분은 푸리에와 디리클레가 각각 증명했습니다.
또한, 식 (7)을 보면 푸리에 계수 $H_m$과 연관된 것이 $m$번째 주파수($\exp(i m \omega_0)$)입니다. 그래서 $H_m$을 보면 $m$번째 주파수의 특성을 알 수 있습니다.
삭제네 이해했습니다. 그런데 MATLAB 코딩중 답을 구하지 못한게 있어서 전파거북이님께 질문을 드리고싶은것이 있습니다.
답글삭제====================================================================
Fs = 3000; % Sampling frequency
T = 1/Fs; % Sample time
L = 10000; % Length of signal
t = (0:L-1)*T; % Time vector
C = 2;
w_m1 = 2*pi*100;
w_m2 = 2*pi*10;
m_1 = 2;
m_2 = 2;
M_1 = 0.01;
M_2 = 0.01;
psi_1 = 10;
psi_2 = 15;
w_THz = 2*pi*1e12;
phi_1 = 10;
phi_2 = 15;
x = C* (1+M_1*sin(w_m1*t + psi_1)) .* (1+M_2*sin(w_m2*t + psi_2)) .* cos(w_THz*t + m_1 * sin(w_m1*t + phi_1) - m_2*sin(w_m2*t + phi_2));
NFFT = 2^nextpow2(L);
X = fft(x,NFFT)/L;
f = Fs/2*linspace(0,1,NFFT/2+1);
plot(f,2*abs(X(1:NFFT/2+1)))
xlabel('Frequency (Hz)')
ylabel('|X(f)|')
===================================================================
를하면 Fs에따라 몇 Hz에서 magnitude를 크게 갖는지 다릅니다.
http://cafe.naver.com/circuitsmanual/107240
위 링크 글이 보이실지 모르겠지만,
Fs = 100, 200, 500, 1000, 2000, 4000 일때 200에서 가장 크게 뛰고 그리고 400에서 뜁니다. 단순히
freq를 어디까지 보여주는지 차이지만
Fs = 3000 일때 1000큰처에서 뜁니다..
Fs = 5000 할땐 또 다르게 바뀌고요
Fs 를 어떻게 설정해야할지 모르겠네요, 더불어 L도 마찬가지고요
복사해주신 코드를 제가 정확하게 보기는 어렵고요...
삭제한 가지만 말씀드리면 Fs를 표본화 주파수라 했고, 관심 신호는 테라 헤르츠가 들어가고 있습니다. 이 둘을 비교하면 표본화 주파수가 너무 작아요. 표본화 이론에 의하면 테라 헤르츠보다 2배 빠르게 표본화 주파수를 설정해야 됩니다.
안녕하세요. 해당 부분을 공부하고 있는 학생인데요. 위에는 없는 내용인거 같지만 푸리에 급수 관련되 것이라 질문 해볼게요 ㅎ;
답글삭제푸리에 시리즈 미분 공식 부분인데요.
x(t) 의 푸리에계수를 Ak라고 하면
dx(t) / dt =>푸리에계수=> jk2(pi)f*Ak
인 공식때문인데요.
그렇다면, t+1와 t는 미분을 하면 두 식 모두 1이 되어 푸리에 계수가 같게 되는데
실제로는 달라야 정상이네요.
혹시 이부분 답변 해주실 있을까요?
첫부분은 정확히 맞습니다.
삭제두번째 질문하신 $t+1$과 $t$는 어떤 의도인지 잘 이해가 안가네요. 좌표 변환이라면 서로 계수가 다를 수 있지요.
f(t)의 푸리에 계수 => ak
삭제g(t)의 푸리에 계수 => bk
d f(t) / dt = 1 의 푸리에 계수 => jk2(pi)f*ak
d g(t) / dt = 1의 푸리에 계수 => jk2(pi)f*bk
두식 모두 1의 푸리에 계수 이므로
jk2(pi)f*ak = jk2(pi)f*bk
따라서, ak = bk [ t의 푸리에 계수 = t+1의 푸리에 계수 ]
그런데 ak 와 bk는 같아서는 안될거 같은데...
저는 이렇게 생각했습니다. ㅠㅠ
아 위에서 f(t) = t, g(t) = t+1입니다.
삭제같아진 이유는 푸리에 급수 때문이 아니고 미분 때문입니다. 적분하면 적분 상수가 있기 때문에 $f(t), g(t)$는 같지 않습니다. 적분해서 상수를 결정해보세요. ^^
삭제음.. ㅎ 잘모르겠네요;;
삭제t와 t+1은 다른 식이니까 f(t)와 g(t)는 다르다는 것은 알겠습니다.
다만, ak=bk가 되는게 이상합니다.
f(t)와 g(t)는 상수부분이 다른 엄연히 다른식인데, 푸리에계수 미분공식을 가지고 이둘의 푸리에 계수를 구했을때 같게 나오는 것이 이상합니다.
상수 부분만 다른 두 식을 미분 하면 상수부분이 없어지고, 이 미분한 식들을 가지고 푸리에 계수를 구하면, 없어진 상수부분때문에 푸리에계수가 같을수도 있다고 생각합니다.
그렇다면, 이 공식이 잘못된 것은 아닐테고, 제가 빠트린 부분이나, 아니면 공식상 전제조건이 있는가 궁금합니다.
위에도 있듯이 미분한 후의 관계식으로 푸리에 계수를 결정하면 시간의 상수항이 사라집니다. 이때는 다시 적분한 후 $f(0) = 0, g(0) = 1$을 이용해 적분 상수를 결정하면 됩니다.
삭제이것은 푸리에 계수와는 관계없고 단순한 미분, 적분 관계입니다.
계속 고민해봤는데 음.. 좀더 공부를 해야겟네요; ㅎ;
삭제주기가 3인 주기함수 g(t)=t+1, 0<t<1 / 0 , 1<t<3
인 식의 푸리에계수를 구하는 것이 문제입니다.
이것의 푸리에 계수를 구할때, (t+1) * exp(-jk2(pi)ft)가 부분적분을 해야하므로
계산을 쉽게 하기 위해서,
g(t)를 한번 미분한 d(t+1) / dt = 1의 푸리에 계수를 구하여.
결과값에 1 / 2k(pi)f 를 곱해주자. 라고 생각했습니다.
그래서, 해당 구간에서 1의 푸리에 계수 ak를 찾았을때,
ak에 1 / 2k(pi)f를 곱해주어 g(t)의 푸리에 계수를 찾았습니다.
하지만, 실제로 g(t)를 미분하지 않고, 푸리에 계수를 구했을 때와
g(t)를 한번 미분해서 푸리에 계수를 구하고 1 / 2k(pi)f를 곱한값을
찾았을 때는 두 값이 다르게 나왔습니다.
생각을 해보니, 이런식이라면, t, t+1, t+2 와 같은 t+c꼴의 모양의 식들은
푸리에 계수가 똑같이 나오게 됩니다. 하지만, 실제로는 그 값들이 다릅니다.
[그 예를 들면, t-1은 t를 1만큼 이동한것이므로, (타임 쉬프트)
t의 푸리에 계수가 bk라면,
t-1의 푸리에 계수는 bk*exp(-j*2*pi*k) 가 됩니다.]
말씀하신, 다시 적분하여 적분상수를 구하라 하신 부분에서
다시 적분을 하면, 제가 원하는 방식인 t+1을 미분하여 푸리에 계수를 구하려는
취지와 맞지가 않는 것 같습니다. 계속 답변해드리게 만들어 죄송합니다.;;ㅠ
푸리에 급수는 해석적인 방법이라 어떤 방식으로 계산하든지 제대로 했으면 답은 동일합니다.
삭제답을 찾는 방법은 여러 가지가 있으니 원칙에 따라서만 하면 어쨌든 답은 얻어집니다. ^^
위에서 말한 내용을 수식으로 쓰면 다음과 같습니다.
$\frac{dh(t)}{dt} = \sum_{m=-\infty,m\ne0}^{\infty} H_m' e^{j m \omega_0 t}~ \Rightarrow ~h(t) = \sum_{m=-\infty, m\ne0}^{\infty} \frac{H_m'}{j m \omega_0} e^{j m \omega_0 t} + C$
적분 상수 $C$는 사실 시간 불변 성분이기 때문에 $h(t)$를 한 번 적분하여 얻을 수도 있습니다.
도와주신 덕분에 어느정도 해결된거 같습니다.
삭제한참 고민한건데 친절히 알려주셔서 드디어 알거 같네요.
감사드립니다.ㅎ
안녕하세요. 가끔 검색하면 좋은 글들이 나와서 늘 잘 보고 있는데, 오늘은 보다가 궁금한 게 생겨서 질문드립니다.
답글삭제위의 어느 댓글에도 나와있는데, 디리클레 커널을 [-pi,pi]에서 적분하면 2pi가 나오는 증명에서, 복소지수를 이용하여 잘 정의된 함수라 적분이 문제가 없다고 하셨는데(아마 분모가 0이 되는 부분이 있어도 상관없다는 의미이신 거 같은데) 이게 무슨 말씀인지 잘 모르겠어요.
이전부터도 이런 sinc func. 형태에서 분모가 0인 경우에 대해 로피탈을 이용해서 답을 구하긴 했었는데 그렇게 해도 되는 근거를 잘 모르고 해왔었거든요.
그리고 식 (18)에서 , t != t'이면 g(t)가 연속인 것은 이해가 가는데, g(t')=lim t->g(t)라고 쓸 수 있는지 모르겠어요. g(t')은 정의될 수 없는 거 아닌가요??
1. 분모가 0이 되는 것이 꺼림직하면 식 (13)을 보세요. 복소 지수 함수의 합으로 정의하면 $t = 0$이 되더라도 문제 없습니다.
삭제2. $g(t)$가 모든 점에서 연속이라는 뜻은 아닙니다. $t = t'$를 포함해서 $g(t)$가 모든 점에서 유한한가라는 관점으로 증명하고 있습니다.
근데 정말 어렵긴 하네요. 제가 신호와시스템을 배울 때에, 교수님이 x(t)=integral X(jw) e^jwt dt 가 된다고만 하고 아무 설명 없이 그 이후를 전개해 버려서 그 이후의 내용을 이해해서 체계를 갖춰도, 저 근본적인 부분에 대해서 증명이 없으니 답답하고 붕 뜬 느낌을 늘 받았었는데 오늘 그 근거를 발견했어요.
답글삭제다만 마음 깊이 받아들이는 건 시간이 좀 더 필요하겠네요...
거북이님..진심으로 책 하나 내시면 안되나요ㅜ
답글삭제여기에 있는 것이 사실상 책입니다, 익명님. 언제든 볼 수 있고, 수정할 수 있고. ^^
삭제전파거북이님 안녕하세요. 푸리에 해석을 공부하고 있는 학생인데 궁금한 점이 생겨서 질문드립니다. 푸리에 급수로 어떠한 함수를 모델링 했을 때, 기존 함수와 이를 푸리에 전개한 함수의 그래프가 일치하지 않습니까? 그런데 공학수학 교재에 있는 푸리에 전개 예제들을 보니, 원래 함수를 푸리에 전개한 결과가 상당히 복잡하다는 것을 발견했는데요. 즉, 사인, 코사인 등의 초월함수에 구간이 무한대인 시그마 또는 인테그랄 연산을 하게 되는데 이 경우에 기존 함수처럼 단순히 임의의 x 값을 넣어서 함수 값을 구하는 것이 불가능하지 않나요? 다시 말해서 푸리에 급수나 푸리에 적분의 경우 기존 함수를 모델링 하고는 있지만, 실제로 특정 x 값에 대해서 함수 값을 구하는 것이 불가능 한 것인가요?
답글삭제지적하신대로 함수값을 정확하게 얻으려면 무한 급수를 계산해야 합니다. 하지만 이건 현실적으로는 불가능합니다.
삭제다만 참값과 근사값과의 차이는 푸리에 급수의 항 개수를 증가시키면 항상 줄어듭니다. 근사중에서 푸리에 급수 기반 근사는 성능이 좋은 편입니다.
푸리에 급수는 n을 1씩 증가시키면서 각각의 항을 구하는 방식으로 정확도를 높여갈 수 있는데, 푸리에 적분(not 푸리에 변환)의 경우는 어떻게 되나요? 푸리에 적분으로 함수를 모델링 했을 때, 적분 자체가 굉장히 난해하여 풀기가 상당히 어렵더라구요. 교재에서는 푸리에 적분이 해석적인 방법으로 적분하기 어려운 식의 적분값을 구하는, 하나의 공식으로서 이용된다고 하는데 이는 바꿔 말하면 푸리에 적분 자체를 근사 함수로 이용할 수 없다는 뜻 아닌가요? 푸리에 적분은 다음과 같은 방식을 통해 적분 공식으로서 이용되는데요... { (1) 임의의 x에 대하여 함수값 f(x)를 미리 알고 있고 (즉, 기존 함수가 무엇인지 안다는 뜻) (2) f(x)를 푸리에 적분으로 전개하여 (3) 전개한 푸리에 적분에 x를 대입하고 (4) 이 수식의 값이 (1)의 값과 같다 } 앞서 말씀 드렸듯 특정 적분을 푸리에 적분으로서 풀이하는 것 자체가 이미, f(x)의 함수값을 미리 알고 있지 않은 이상은 푸리에 적분을 풀이할 수 없다는 것 아닌가요?
삭제푸리에 적분도 비슷하게 생각할 수 있습니다. 어차피 근사할 때는 컴퓨터를 쓰기 때문에 적분도 수치 적분으로 교체합니다. 이 수치 적분의 구간을 줄여가면 푸리에 적분을 오차를 줄이면서 구할 수 있습니다.
삭제통신에서는 원래의 시간 함수 $f(t)$를 알기 어렵기 때문에 주로 주파수 대역 특성($F(\omega)$)을 봅니다. 이때 쓰이는 장비가 주파수 대역 분석기(spectrum analyzer)입니다.
다시 말해서, 거북님 말씀은 ***푸리에 적분은 기존 푸리에 급수와 달리 일반적인 방법으로 풀이하기는 어려우나*** 컴퓨터 상에서 수치 적분을 통해 근사 함수로 이용할 수 있다는 말씀이신가요?
삭제수치 적분도 믿을 만합니다. 오히려 무한 급수보다 적분이 더 좋은 결과를 도출하는 경우가 많습니다. 전자파 해석에 사용하는 GTD(회절에 대한 기하 이론, geometric theory of diffraction) 같은 것이 좋은 예입니다. 원통 좌표계에 대한 무한 급수는 매우 느리게 수렴하지만 회절 적분은 빠르게 수렴시킬 수 있습니다.
삭제질문 있습니다!
답글삭제식(6)에서 (7)로 넘어가는 과정에서 Hm을 m의 범위에 따라 세부분으로 나누셨는데요.
m=0, m>0일때는 이해가 되는데
m<0일때 (G-m + iF-m)/2 이렇게 -부호가 아닌 +부호로 나오는게 잘 이해가 되지 않습니다.
단순하게 생각하세요, 익명님. ^^
삭제지수 함수에 $-m$으로 표시된 항을 모으면 됩니다. 분모에 있는 $i$가 분자로 올라오면 $-i$가 되어 식 (6)이 쉽게 얻어집니다.
안녕하세요^^ 통신공학을 공부하지는 않지만 푸리에분석에 대해 알아보려고 여러가지 글을 읽고있는 한 사람입니다. 그런데 푸리에 분석에서 1-Dimensions와 3-Dimensions 이 있더라구요.(식 전개과정에서 읽었습니다.) 식 자체는 이해가 가는데 여기서 왜 굳이 1차원과 3차원으로 구분을 나누는 이유가 있는 건가요?? 차이점이라던지.. 그리고 그러면 왜 2차원은 없는건가요...?? 좀 이상한 질문일수도 있겠지만 궁금해서 질문합니다..ㅠㅠ
답글삭제2차원도 당연히 있습니다, 익명님. ^^
삭제푸리에 급수는 미분 방정식을 풀기 위해 제안된 개념이라서 변수가 하나일 때는 1차원, 두 개는 2차원, 세 개는 3차원 등등으로 분해해서 풀 수 있습니다.
아하~! 저는 단순히 차원이라는 말이 언급됬길래 공간의 차이인가 라는 생각만 막연히 했었는데 그런 이유때문에 차원이 나뉘는 거였네요. 친절한 답변 감사드려요 ^^
삭제전파거북님 궁금한게 한가지 있어요 !
답글삭제주기함수를 다루는 푸리에 급수에서
이산시간의 주기함수를 다룰 때는 연속시간의 주기함수와는 다르게 N개의 구별된 정현파 함수를 갖는다고
하잖아요. 그럼 주파수 도메인으로 나타날 때도 N개의 주파수 성분만 나타나면 되는데 왜
N 주기의 주파수로 나타나는 건가요? 수식으로 풀어보면 e^(jkΩn)에 k 대신 k+N을 대입하여 구해보면 똑같
e^(jkΩn)가 나옴을 확인할 수 있고 이를 통해 주파수는 N만큼만 존재하고 그 배수 의 경우는 반복이란 것을
알 수있는데요. 이거를 상황적으로는 이해 를 못하겠는데 굳이 그렇게 까지 이해할 필요가 없는 부분인
가요? 아니면 설명이 가능하시다면 부탁 좀드릴게요 감사합니다.
DFT 분야에서 아주 중요한 질문입니다.
삭제원칙적으로 무한대의 주파수 성분이 있어야 원래 신호를 표현할 수 있습니다. 여기서 중요한 부분은 모든 시간을 표현하고자 할 때입니다.
만약, 우리가 모든 시간을 포기하고 시간 표본을 $M$개만 이산적으로 추출한다면 푸리에 계수도 $M$개만 얻을 수 있고, 나머지는 반복됩니다. 이게 타당한 것인가를 고민해야 하고, 그래서 발견한 것이 나이퀴스트(Nyquist)와 섀넌(Shannon)이 제안한 표본화 정리입니다.
안녕하십니까? 존애하는 전파거북이님께 질문을 드리고자 글을 남깁니다..
답글삭제저는 이 엄청난 게시물의 기본인지는 모르겠으나, 식(1)과 식(2)에 대해 이해가 안갑니다.
저는 식(1)를 통해 식(2)를 유도하려고 했으나, 어떤 수학적 오류발생한지 잘 모르겠습니다.
일단 저는 식(1)의 양변에 식(2)의 첫줄의 식을 적용시켜 (·)부분에 f(t)를 넣어서 푸니 좌변은 괜찮은데,
우변은 (무한합 F_m)이 있는데 이것이 적분 밖으로 나갈수있는지 잘 모르겠습니다.
만약 나간다 해도 (무한합 F_m)*(T/2)가 되어서 T/2를 좌변으로 넘기면 식(2)의 넷째줄 우변과 일치하는데
좌변은 F_m 이 아닌 (무한합 F_m)이 됩니다.
분명이 저의 미천한 지식때문에 일어난 오류같은데 어디서부터 오류가 발생된지 모르겠습니다.
존애하는 전파거북이님! 그대의 도움으로 저를 이 연옥으로부터 해방 시켜주시옵 소서.
-오시 올림-
아 해결이 되었습니다... 이딴걸 질문 드려서 송구합니다..
삭제쫌만 생각해보면 될것을.........ㅠㅜ
-오시 올림-
오시님, 혼자 해결하시는 것이 제일 좋습니다. 혼자 고민하면 사고가 깊어집니다. ^^
삭제안녕하세요 너무 혼자고민을 오래해서 하나만 여쭐게요 ㅠㅠ sin급수 cos급수를 합쳐서 복소 퓨리에를 만들었는데 여기에서 exp^jwt꼴이니까 이 복소수의 Re파트만 실제 신호인가요? 결국엔 페이져표기가 되었으니까 이게 맞는것같기도 한데 ㅠㅠ
답글삭제김기남님, 원칙적으로는 아닙니다.
삭제복소 지수 함수가 완비성을 가지기 때문에 임의의 복소 함수를 푸리에 급수로 전개할 수 있습니다. 또한, 실수도 복소수에 포함되기 때문에 실수부를 취하는 연산을 하지 않더라도 복소 지수 함수 기반 푸리에 급수는 실수 함수를 전개할 수 있습니다.
식 (13) 등비급수 공식 말인데요, a*(r^0-r^n)/(1-r) 아닌가요?
답글삭제말씀하신 등비 급수 공식을 써서 만든 식입니다. 다만, 제시하신 식에서 $n$은 $n+1$이 되어야 합니다.
삭제제가 바보라서 그런지 모르겠지만.. 디클렐레 방법은 뭔가 논리적으로 확 와닿지가 않네요.. 식 (15)는 정의고, partial sum Sm이 f(t)로 수렴한다는 것 조차 식 (15)를 Sm과 f(t)에 그대로 적용해서 썼기 때문에 뭔가 당연한 결과가 나온 것 같은... 제가 바보라서 그럴까요... 뭔가 식 (15) 정의가 선행되고, 디클렐레 방법은 푸리에 급수 구조만 보여주는 것 같은 느낌이..
답글삭제고민을 해야 발전합니다, 이재님. ^^
삭제식 (15)는 정의가 아닙니다. 식 (15)의 좌변과 우변이 같을 이유는 없습니다. 이 명제를 증명하는 기법이 디리클레 방법입니다.
전 바본가봐요 ㅠㅠ 어디서 잘못했는지 알아 냈어요. 항상 감사합니다!
삭제확실히 Hilbert space를 공부하고 Fourier transform을 다시 보니 이해되는 속도가 빠르네요
답글삭제Jung Woo님, 힐버트 공간과 푸리에 변환을 연결하기가 쉽지 않은데요, 대단하시네요. ^^
삭제안녕하세요 전파거북이님. 정말 헤메고헤메다 찾아오게 되었습니다. 전 해양쪽을 배우고있는 공대생입니다. 질문이 있습니다 .. 푸리에 이론으로 임의의 주기함수 f(x)를 계수Fm으로만 결정해서 통신처리가 쉽다고하셨는데, 이것이 mp3 음악소스나, 동영상소스 등을 압축하는 원리랑 같은것인가요? 기존의 음악소스를 푸리에함수로 바꾸어 sine, cosine의 합으로만 나타내는것이 압축하는것의 원리인지 ..혼자서 푸리에를 배우려니 정말 쉽지가 않습니다 ..ㅠㅠ
답글삭제또한 깁스현상..그 탁 튀어오르는 그 현상은 왜생기는지.. 실제적으로 어떻게 완화시키는지 궁금합니다..
1. 푸리에 급수 혹은 변환은 압축에 쓰일 수 있는 유용한 기법입니다. 관련해서 아래 링크 참고하세요.
삭제http://ghebook.blogspot.kr/2012/08/fourier-transform.html
2. 깁스 현상은 불연속점이 있는 조각 연속 함수(piecewise continuous function)를 푸리에 급수로 표현했기 때문에 생깁니다. 대표적인 것이 구형 함수(rectangular function)의 푸리에 근사입니다. 깁스 현상은 불연속점이 원인이므로 원함수의 급속한 변경을 제한하면 튀는 현상은 줄어듭니다. (물론 원함수의 불연속 특성 일부가 상실됩니다. ) 예를 들면, 저역 통과 필터(low pass filter)를 통과시킬 수 있습니다.
식(9)에서 2번째 식에서 3번째 식으로 넘어과는 과정이 이해가 잘 안되요 도와주세요 ㅠㅠ
답글삭제3번째 식에서 사라진 2번째 식의 가운데 두항에 대해서 설명좀 해주실수 있을까요??
중간항이 사라졌다기 보다는 "A - B - B + B = A - B"가 된 것입니다. 여기서 A, B는 두번째 식에 있는 첫째항과 둘째항입니다.
삭제선생님. 안녕하세요. 처음 인사 드립니다.
답글삭제푸리에 급수 공부하다가 이 블로그를 알게 되었는데 읽을 수록 바보가 되는 느낌입니다.
선생님 프로필에 '질문하라'고 적혀 있어서 용기내어 질문을 몇개 드리고 싶습니다. 제가 읽고 있는 푸리에 해석이라는 책에서 몇가지 질문드리고 싶은데 혹시 메일로 질문 드려도 되는지요? 제가 구글 블로그 사용법을 잘 몰라서 그런데 혹시 선생님 블로그 글에 댓글다는 형식 말고 그냥 질문을 올릴 수 있는 방법이 있는지요?
안녕하세요, Steve님. ^^
삭제댓글로 질문하시는 것이 좋습니다. 블로그에서는 다른 방법이 없습니다.
잘 읽었습니다. 감사합니다.
답글삭제퓨리에 급수가 삼각함수와 직접적인 관련이 있는 건가요?
답글삭제아주 밀접한 관계가 있습니다.
삭제삼각 함수에 가중치를 여러 번 곱하면 임의의 연속 함수를 원하는 범위까지 근사할 수 있다는 것이 푸리에 급수입니다.
안녕하세요 거북이님. 질문이 있습니다.
답글삭제식 (23)의 첫째줄은 식 (14)의 적분 변수를 단순하게 바꿈으로써 얻으셨다고했는데요,
-----참고-----
2. 식(23)의 첫째줄에서 둘째줄로 가는게, even 함수특성이 있어서, D_m(t') = D_m(-t') 인것은 알겠는데요. 식(14)에서 식(23)의 첫줄이 어떻게 바꾸는지 아리송해서요.
혹시, 단순하게
f(t') D_m(t - t')에서
t - t' = t_1 , t ' = t - t_1 로 해서
f( t - t_1 ) D_m( t_1 )
다시 t_1 ==> t' 해서
f( t - t' ) D_m( t' )
이렇게 하는건가요?
-------------------------라는 곰유님의 질문에 맞다고 답하셨습니다.
근데 t-t`를 t_1로 치환하는 과정에서 -dt`=dt_1이고, 적분범위도 -pi 에서 pi 가 아니고 달라지지않나요?
하 이 글을 읽으며 정말 많은 질문들이 생겨났다가 혼자 고민하는 과정에 사라지고를 반복하고 있습니다. 생각하는 힘이 강해지고 있다는 걸 몸소 느낄 수 있네요. 여전히 질문이 허접한 건 이해 부탁드립니다. ㅜㅜ
네, 특별할 것 없는 단순한 변수 치환입니다. ^^
삭제전파거북이님 항상 좋은 글 감사합니다! 읽어내려가다 궁금한 점이 생겨 여쭙니다.
답글삭제식 18에서 함수 g를 정의해서 수렴성을 확인한 다음 sin항과 곱해서 연산했을 때 0으로 수렴하여 증명한다고 이해했습니다.
그런데 수렴성을 판단할 때 식을 쪼개서 각각을 판단하는 것이 논리적으로 정확하다고 볼 수 있나요?
식을 쪼갰다기 보다는 리만-르베그 보조 정리를 적용하기 위해 $g(t)$가 리만 적분 가능한지 판단한 것입니다.
삭제감사합니다, 전파거북이님.
삭제끝까지 읽지도 않구 너무 성급했네요...
빠른 답변 감사합니다!
작성자가 댓글을 삭제했습니다.
답글삭제복소 지수 함수의 합을 구한 다음에 오일러 공식을 적용하면 됩니다.
삭제안녕하세요.전파거북이님. 항상 귀중한 자료 올려주신 것 감사드리고 있고 forier 급수도 잘 보고 있습니다. 다름아니라, 본 내용과 더불어서 개인적으로 여러 수리물리학이나 공학수학책을 보니, 다변수 함수의 경우도,푸리에 전개가 가능하다고 하는데, 증명은 다들 없고, 제곱적분 기능할 경우 푸리에 전개가 된단 식으로만 되어 있더군요. 그렇게 해놓고는 그냥 사용하는 위주로 서술되어 있는게 대부분인거 같습니다.
답글삭제다변수 함수에 대한 푸리에전개의 경우 증명과정은 위의 내용과 비슷한 수준이나 방식을 따르게 되는건지 궁금해서여쭤봅니다. 바쁘신 중에 답주시면 정말 감사하겠습니다.
다변수 함수라고 모두 푸리에 전개 가능한 것은 아닙니다. 핵심은 변수 분리(separation of variables)입니다. 이 개념은 오일러, 푸리에 등이 사용한 재미난 수학적 기교입니다.
삭제변수 분리법에 대한 예시는 아래 참고하세요.
https://ghebook.blogspot.kr/2012/07/heat-becomes-communication-heat-equation.html
넵. 바쁘신 중에 답주셔서 감사합니다!
삭제말씀하신 것과 같이 공학수학이나 수리물리학에서 등장하는 편미방을 변수분리법에 의해서 풀어가는 과정에서 경계조건이 적절히 주어질 경우, 자연스럽게 다변수함수가 푸리에전개가 가능한 형태로 되는 것을 볼 수 있네요.
다만 그럼에도 불구하고, 이변수함수 및 그 이상의 n차원에서의 어떤 임의적인 함수가 L2 Space에 있을 경우 n개의 삼각함수나 지수함수가 곱해진 것들의 무한합으로 수렴되는 형태로 표현될 수 있다는 수학적 정리부터가, 처음에 푸리에급수에 대해 찾을때 나와서 좀 어려웠던 것 같습니다.
제대로 찾아보니 stone-Weierstrass approximation theorem이라는 위상수학에서나 증명이 이뤄지는 정리라던가, 그냥
슈뢰딩거방정식 정도나 풀며 hermitian operator의
고유함수들로 span이 가능하다고 공리적으로 알던
Hilbert space에 대한 보다 깊은 지식, 그외 이들을 보조하는 잡다한 수학적 개념들이 개입이 되고서야 증명이 엄밀히 이뤄지는 것이라서 어디까지를 공리적으로 잡아야할지 혼자 시간을 많이 써버린 것 같습니다. ㅋ
다시한번 감사의 말씀드리고 좋은 하루 되시길 바랍니다!
안녕하세요.전파거북이님. 좋은글 정말 잘 보았습니다. 전자과를 다니면서 신호 및 시스템 과목에서 통신이론 까지 푸리에급수를 정말 많이 쓰지만 "그냥 맞다고 하고 써도되나? 왜 이 급수로 표현되는지 모르면 예외상황이 생길때 왜그런지 알수 없지 않나?"라는 의문을 매수업마다 떨치지못해 인터넷을 뒤져보다 들어오게 되었습니다. 본문과정중 한가지 의문이 생기는것이, 디리클레조건에는 확실히 f(t)가 주기함수라는 조건이 있지만 식 (15)를 증명하기위한 과정중에서 주기함수인 조건인 f(t+T)=f(t)를 쓴것이 전혀안보이는데 위 증명을 따라간다면 f(t)가 주기함수가아니고 본문의 T값에 아무값이나 집어넣어도 식 (15)가 성립해야되는것 아닌가요? 밤새고민하다가 인터넷을 찾아보다 알아내지못해서 질문드리게 됬습니다. 답변해주신다면 정말감사하겠습니다.
답글삭제식 (16)은 주기 함수를 가정하고 계산한 거예요.
삭제식 (16)은 디리클레 핵심을 적분한것이니 f(t)가 주기함수인지 아닌지에 관한정보가 없는것 아닌가요....?
삭제디리클레 핵심 정의에 사용한 식 (11)도 보세요. 또한 푸리에 급수 전개할 때 전제로 사용하는 조건이 주기 함수예요. 푸리에 급수 표현식 주기와 $f(t)$ 주기는 같이 설정되어야, 식 (7)의 전제가 성립하게 돼요.
삭제아 그렇군요. 완벽히 이해까지는 아니지만 실마리는 찾은것 같습니다. 완벽한 증명이란 어렵군요.. 감사합니다!
삭제h(t)에서 m이 마이너스 무한대부터로 바뀌는 이유가 -imwt 부분 때문인가요?
답글삭제맞습니다, 익명님. ^^ 식 (7)에 있는 $H_m$ 정의와 식 (6) 최종 결과를 같이 보세요.
삭제좋은 글 감사합니다. 취미로 푸리에 변환을 알아가는 중입니다.
답글삭제위키피디아를 보면 푸리에 수렴은 여러 종류가 있으며 그중 점별,균등,절대 등등의 수렴이 있다고 합니다. 당연히 수렴 조건이 다르지요. 예를드신 수렴 증명은 점별수렴인가요? 아님 균등수렴인가요? 함수 f(t)가 연속이라 하셨는데, 균등수렴을 말하시는 것 같습니다.
f(t)가 그냥 연속이라는 것은 균등수렴에서 충분한 조건이 아니라고 합니다. 반드시 립시츠 연속이 되어야 균등수렴한다고 합니다. 이 경우 푸리에 계수는 절대 합(absolutely summable)이 가능하고 균등수렴한다고 합니다. 의견 부탁 드립니다.
다시 한번 높으신 수학 해석에 감사드립니다.
식 (15)에 있는 좌변과 우변은 (엄밀한 의미에서) 점대점으로 같지는 않아요. 좌변 $f(t)$는 연속 함수입니다. 이건 변함이 없어요. 이걸 푸리에 급수 관점으로 표현한 무한 급수인 우변이 중요해요. 우변이 무한 급수이기 때문에 수렴 조건을 사용하게 됩니다. 본문에 소개하지 않았지만 바이에어슈트라스 M-판정(Weierstrass M-test)을 이용하면, 유한점 불연속 함수의 푸리에 급수는 균등 수렴함을 보일 수 있어요.
삭제빠른 답변에 감사드립니다. 저는 위키피디아를 읽어보고 공부 중입니다.
삭제제가 드린 질문을 좀더 부연 설명 드리겠습니다.
(1) 푸리에 급수 f(t)의 수렴은 f(t)가 유한개의 불연속점을 가질때(한 주기 안에서) 식(15)의 우변은 f(t)로 점별수렴합니다. 또한 그것의 계수 Fm은 리만-리베르그 보조정리에따라 m이 무한대로 갈수록 0으로 수렴합니다.(수렴속도는 O(1/n)에비례) 그러나 이경우 푸리에 계수의 절대 합(absolutely summable)은 발산합니다. 또한 불연속 점에서 깁스현상이 발생하고 불연속점 근처에서는 파상이 발생합니다. 이 파상 때문에 불연속 점근처에서는 f(t)의 좌미분계수와 우미분계수의 평균값으로 수렴한다고 할수 있는지요? 불연속 점이 있으면 절대로 균등 수렴 할수 없습니다.
(2) 급수f(t)가 연속함수 일때, 연속 함수라는 조건만으로 균등 수렴한다고 할수 없습니다.
급수가 연속이며, 홀더조건을 만족 시키거나, 푸리에 계수의 절대 합이 가능하거나, 립시츠 연속 일때 급수 f(t)는 균등 수렴합니다. 균등수렴한다는 것은 계수 Fm의 0으로 수렴 속도가 빠르고 O(1/n^k), f(t)의 모든 점에서 식(15)의 좌/우변의 절대 오차의 최고값이 0으로 수렴한다는 것입니다. 급수f(t)가 단지 연속함수 일때 디리클레 핵심 및 다른 기법으로 증명한 수렴은 균등수렴이라 할수 있는지요?
다시한번 감사드립니다.
애고, 지적하신 내용을 다시 보니 제 답변이 틀렸네요. 죄송하고요, 틀린 부분 지적은 정말 감사합니다. ^^
삭제1. 균등 수렴하려면 $f(t)$는 연속이 되어야 합니다. 또한 $f(t)$의 미분이 존재한다면 $f'(t)$는 유한점에서만 불연속일 수 있고 이외 구간에서는 반드시 연속(piecewise continuous)이 되어야 합니다.
2. 그래서 식 (22)는 모든 점에서 수렴하지만, $f(t)$가 불연속점을 가지면 균등 수렴하지는 않습니다. 그냥 불연속점에서 식 (22)의 좌변만 봐도 균등 수렴하지 않는 게 보이네요.
좋으신 말씀 감사합니다. 첨언 해도 될런지요.
삭제균등 수렴하려면 f(t)는 연속이 되어야 합니다. 또한 f(t)의 미분이 존재한다면 f′(t)는 유한점에서만 불연속일 수 있습니다.
예: f(t)=abs(t), -1<=t<=1 의 주기함수는 연속이며 f’(0)에서 좌미분 계수와 우미분 계수가 다릅니다. 따라서 미분 할수 없습니다. 즉 f′(t)는 t=0에서 불연속 점을 가집니다.
무한급수가 균등 수렴합니다 .
f(t)=sqrt(t), 0<=t<=1의 주기함수는 연속이지만 f’(0)에서 미분값이 무한대입니다.
따라서 미분 할수 없습니다. 그러나 f’(0)에서 상계(upper bound) 값이 없어서
그러므로 무한급수는 균등 수렴하지 않습니다.
친절한 설명 다시 감사드립니다.
허락하신다면 한번더 부연 하겠습니다.
삭제전파거북님께서 하시고자 하는 말씀은
- (1)식이나 (15)식이 항상 성립하는 것은 아니다. 무한급수가 원함수f(t)에 균등 수렴할 경우만 (1)식과 (15)식이 성립한다. (디리클레 핵심과 리만-리베르그 보조정리를 이용하여 간단히 증명가능)
- 무한 급수가 원함수에 균등수렴하기위해서는 원함수가 연속 함수이며 홀더조건을 만족 시키거나, 푸리에 계수의 절대 합이 가능하거나, 립시츠 연속 등등의 조건을 만족 시켜야 한다.
- 만일 원함수 f(t)가 불연속 점이 있거나, 연속 일지라도 위의 균등수렴 조건을 만족 시키지 못하면 무한급수는 점별수렴하며 (1)식과 (15)식이 성립되지 않는다.
- 이 경우 불연속 점에서는 깁스현상이 일어난다.
- 따라서 푸리에 급수에서 (1)식이나 (15)식만 믿지말고 수렴은 매우 중요한 사항이다.
- 수렴이 왜 중요한 문제인가는 많은 산업분야에 푸리에 급수/변환을 적용함에 있어
무한급수는 우리가 다룰수 없고 실제는 한정된 계수를 이용한 부분합을 이용한다. 이경우 부분합이 무한대로 가면 원함수에 수렴하는지는 매우중요하다.
-예를 들어 의료기기 MIR경우 주워진 푸리에 계수(실제는 주파수 영역의 데이터)를 이용하여 사진을 만들어 낸다. 이때 부분합에 불연속 점이 있으면 사진이 왜곡된다. 따라서 왜곡(깁스현상)을 없애기위한 노력들이 있다. 즉 이는 푸리에 수렴과 매우 밀접한 관계가 있다.
- 결론은 푸리에 급수의 수렴은 그냥 수학이 아니라 여러 산업분야에 사용되는 기술의 원천이다.
이런 말씀을 하실려고하셨지요?
제가 애매하게 표현했네요. ^^ 미분이 존재한다는 표현은 미분이 구간마다 연속(piecewise continuous)이란 뜻으로 썼어요.
삭제예로 드신 두번째 함수는 미분이 구간마다 연속은 아니기 때문에 균등 수렴은 M-판정법으로 해야 합니다. 또한 미분이 발산한다고 해서 반드시 균등 수렴하지 않다고 할 수도 없어요. 대표적인 예가 바이에어슈트라스 함수입니다. 이 함수는 모든 점에서 미분이 발산하는데도 균등 수렴해요.
위의 첨언 중 f(t)=sqrt(t), 0<=t<=1는 f(t)=sqrt(abs(t)), -1<=t<=1로 바꿉니다. 허둥대다보니 실수가 나오네요. 그리고 f(t)는 실수(real number) 입니다.
삭제위키피디아에 있는 바이에어슈트라스(Weierstrass) 함수를 읽어보겟습니다.(내일 예정)
삭제바이에어슈트라스(Weierstrass) 함수를 읽어본 바에 의하면
삭제Weierstrass function is well known that this function is uniformly continuous everywhere but differentiable nowhere.
라고 합니다. 여기서
Lipschitz continuous ⊆ α-Hölder continuous ⊆ uniformly continuous 입니다.
따라서 모든 립시츠 연속은 균등 연속입니다. 그러나 모든 균등 연속은 립시츠 연속이 아닙니다. 따라서 바이에어슈트라스 함수는 균등 연속이지 립시츠 연속이 아닙니다.
당연히 바이에어슈트라스 함수는 단지 균등 연속이지 균등 수렴하지는 않습니다.
왜냐면 수렴값이 발산하기 때문입니다.
결론: 바이에어슈트라스 함수는 단지 균등 연속, 립시츠 연속은 균등 수렴
정정: 왜냐면 미분값이 발산하기 때문입니다.
삭제죄송합니다. 위키피디아 읽어보니 제가 틀렸습니다.
삭제Weierstrass function를 푸리에 무한급수라보면 무한급수는 균등수렴합니다.
이유는 Weierstrass M-test를 하여보면 알수 있습니다.
Weierstrass 함수의 푸리에 급수 계수를 Fn=a^n이라하면 계수의 절대합은 수렴합니다.
따라서 Weierstrass function는 균등수렴합니다.
앞으로는 아는척 하지 않겠습니다.
Unknown님, 계속 치열하게 고민하시고 공부하시길 바랍니다. ^^
삭제어쨌건 제가 공부해보면 푸리에 급수는 수학, 물리학, 공학에서 가장 중요한 개념입니다. 계속 열공하세요.
질문 하나더 드려도 될까요?
답글삭제불연속 점이 있는 경우(22. 유한점 불연속 함수와 푸리에 급수)
“함수 f(t)가 유한한 점에서 불연속이면 다음 푸리에 급수가 반드시 성립한다.”
즉 특정한 점f(t1)의 좌미분계수와 우미분계수의 평균값으로 수렴한다고 해석 됩니다.
여기서 불연속점에서 깁스현상이 일어나고 파상(overshoot)이 나타난다고 합니다. 이 파상의 크기는 불연속 점에서 좌미분 계수와 우미분 계수 차이의 9% 라고 합니다. 또한 급수가 무한대로 가더라도 이 파상은 없어지지 않는다고 합니다. 따라서 깁스현상 때문에 불연속점 근처에서는 푸리에 급수는 f(t1)의 좌미분계수와 우미분계수의 평균값으로 수렴하지 않는다는 생각이 듭니다. 어떻게 생각하시는지요?
감사합니다.
1. 위 답글에 쓴 "식 (15)에 있는 좌변과 우변은 (엄밀한 의미에서) 점대점으로 같지는 않아요"를 고민하시면 답을 얻을 거예요. 즉 푸리에 급수 접근법에서는 식 (15)가 아닌 식 (22)로 표현한 좌변과 우변이 같아요.
삭제2. 연속 함수와 미분 가능을 고려한 푸리에 급수는 다른 문제입니다. 바이에어슈트라스 함수(Weierstrass function)로 한 번 검색해보세요.
삼각함수의 직교성이라는 말이 사인함수와 코사인함수의 위상차가 말그대로 90도인 부분과 연관성이 있나요?
답글삭제그렇다고 볼 수 있지만, 정확히는 삼각 함수 합차 공식 때문에 직교성이란 특징이 생겨요.
삭제공업수학 책을 보니 삼각함수 시스템의 직교성 파트에 바로 합차 공식으로 보여주는 게 나오네요
삭제언제나 성실한 답변 감사드립니다. 덕분에 좀 더 공부할 의욕이 생깁니다
안녕하세요, 시그널 프로세싱을 공부하고 있는 학생입니다.
답글삭제다름이 아니라, cos(wt)를 FT하게 되면, sine 부분은 없기 때문에, 결과가 실수 + 허수로 나타날 때, 허수는 모든 구간에서 0이 되는 것이 맞나요? 그리고 그에 따라 위상은 0도 or 180도가 되어야 하는 것이 맞는가요?
맞습니다, 박준용님. ^^
삭제안녕하세요. 항상 많은 도움 얻어가고 있습니다.
답글삭제글을 읽던 중 이해가 가지 않는 부분이 생겨 질문을 드리고 싶은데요, 식(23)에서 적분 변수를 바꾸는 과정은 알겠지만 어째서 적분 구간은 그대로인지 잘 모르겠습니다.
반가워요, Unknown님. ^^
삭제식 (23)은 각(라디안)에 대한 적분입니다. 그래서 적분 구간이 360도($= 2\pi$) 범위라면 어떻게 잡더라도 적분값은 동일해요.
간단한 원리였군요. 감사합니다.
삭제9에서 10으로 넘어가는 베셀부등식 증명을 좀 더 설명 해주실 수 있나요?
답글삭제그리고 13번도 설명좀 부탁드려요
1. 식 (10)은 식 (9)를 이항해서 구합니다. 단순한 부등식이에요.
삭제2. 식 (13)은 등비 급수와 오일러 공식을 이용해 보세요, 응집물리님. ^^
안녕하세요. 항상 좋은 포스팅 잘 보고 있습니다.
답글삭제질문이 있어서 댓글 남기게 되었는데요.
식 (28)을 증명할 때 Dirac delta function은 piecewise continuous하니까 식(22)를 이용해야 되겠다고 생각을 했습니다.
그러다 보니 문제가 생겼습니다.
식(22)에서 f=Dirac delta function이라고 하면 {f(x+)+f(x-)}/2 가 항상 0이 됩니다.
f가 나와야 Dirac delta function = Dirichlet Kernel 꼴로 나와 증명이 되는데 말이죠.
이 문제에 대해 도움주시면 감사하겠습니다.
조각마다 연속은 [그림 1]과 같은 함수입니다. 디랙 델타 함수는 유계가 아니라서(예를 들어 $x = 0$에서 발산) 식 (22)에 집어넣을 수 없어요.
삭제답변 감사합니다.
답글삭제그렇다면 디랙 델타 함수는 연속이지도, 조각마다 연속이지도 않은데 어떻게 퓨리에 급수를 이용해서 표현할 수 있는지 궁금합니다.
저는 퓨리에 급수의 수렴성을 연속이거나, 조각마다 연속인 모든 함수를 표현할 수 있다로 이해했거든요.
좋은 질문입니다. 그 질문에 대해 논리적인 답을 한 수학자는 수학의 노벨상이라는 필즈상을 받았어요.
삭제디랙 델타 함수가 된다고 했지만, 정확하게는 푸리에 급수의 완비성을 표현하는 표기법이라고 보면 됩니다.
아래 링크도 참고로 보세요.
https://ghebook.blogspot.com/2011/10/dirac-delta-function.html
거북이형님 감사합니다.. 우연히 이 블로그를 알게되었는데 이글을 시작으로 한 3시간동안 여러 글을 보느라 시간가는줄도 몰랐네요... 덕분에 배웠던 내용들 복습하고, 앞으로 배울 내용들 예습해가는거 같습니다ㅎㅎ 제 지식에 빈틈이 상당히 많았다는걸 알게되었습니다.. 감사합니다
답글삭제방문 감사합니다, 익명님 😉 꾸준히 열공하세요~~
삭제안녕하세요 좋은 포스트 보고 감명받았습니다. 임의의 함수에 대해 퓨리어 급수를 어떻게 놓고 푸는지 찾다가 왔는데, 질문이 있습니다. 어떤 논문에 보니, 극좌표에서 r*sin(theta)를 SIGMA from n=-inf to inf [(f_{n-1}-f_{n+1})*exp(i*n*theta)]의 퓨리어 급수 형태로 가정해서 미분방정식을 풀었더라구요. 여기서, f_{n}은 미정계수이구요, n은 급수에 쓰인 변수를 아랫첨자로 표현한 것 입니다. 또, 유사하게 r*cos(theta)는 SIGMA from n=-inf to inf [(f_{n-1}+f_{n+1})*exp(i*n*theta)] 로 표현해서, 두 미정계수 f_{n-1}과 f_{n+1} 사이에 차를 합으로만 바꾸어 놨던데, 이 부분을 좀 설명해 주실 수 있으신가요?
답글삭제오일러의 공식을 이용해 삼각 함수를 복소 지수 함수로 풀어보세요. 식 (6)과 비슷할 것 같아요.
삭제아 그렇구요. 아랫첨자에 n-1, n+1이 있는 부분이 너무 생뚱맞아서 이해가 안됐는데, r이 exp(i*n*theta)에 대응되고, sin(theta)가 {exp(i*theta) - exp(-i*theta)}/(2i)로 변환되니까, 계수의 아랫첨자가 (n-1), (n+1)이 남아 있었던거네요. 공부하는데 필요한 많은 지식들을 배워갑니다. 정말정말 감사해요.
삭제안녕하세요. 푸리에 급수 증명 관련해서 10년째 고민하고 있습니다.
답글삭제보통 인터넷이나 책 보면 삼각 함수의 직교 성질을 이용하여 삼각함수 앞의 계수를 구하는게 전부입니다.
하지만 이것으로는 충분하지 않지요.
제가 알고 싶은 것은 사인파와 코사인파의 조합만으로 정말 모든 형태의 주기 함수를 표현할 수 있느냐? 라는 것 입니다.
이것에 대한 증명은 아무리 찾아도 없더군요.
윗 글에 ( f(t)+f(-t) )/2 + ( f(t)-f(-t) )/2 = f(t) 인 성질을 이용하면 증명할 수도 있을거 같은데 . . . 잘 모르겠네요.
푸리에 급수에서 사인파 합계 부분이 ( f(t)-f(-t) )/2 이고 , 코사인파 합계 부분이 ( f(t)+f(-t) )/2 라고 이해하면 되나요?
그렇다면 이 부분에 대하여 증명이 가능할까요 ?
식 (15)와 (22)에 증명이 있어요.
삭제어렵네요 ㅠㅠ
삭제공대생 출신들도 쉽게 이해할 수준의 증명은 없나요 ?
좀 더 간단한 증명이면 좋겠는데요 ㅠㅠ
참고 링크라도 걸어주시면 고맙겠습니다.
Unknown님, 제가 공부한 바로는 본문의 증명이 가장 쉬워요.
삭제현대 수학에 입문한다 생각하시고 증명에 집중하시면 많은 경험을 쌓을 수 있어요.
선생님 좋은 글 정말 감사합니다 아직 이해는 잘 못했지만 두고두고 읽으러 오겠습니다*^^*
답글삭제시간을 가지고 천천히 가셔도 됩니다. 인생은 길어요 ^^
삭제식 (14)를 이용하여 식 (23)을 유도하는 부분이 잘 이해가 안 되어 질문 드립니다.
답글삭제t-t'을 k로 변환한다고 하면 t-t' = k 이고 t'의 범위가 (-pi, pi)였으므로 k의 범위는 (t+pi, t-pi)가 되고
d(t') = d(t-k) = d(-k)이므로 적분은 f(t-k)*Dm(k)*d(-k)이고 적분 범위는 (t+pi, t-pi)이므로
최종적으로 정리하니 f(t-k)*Dm(k)*d(k)이고 적분 범위는 (t-pi, t+pi)인 적분 함수가 나왔습니다.
그런데 식 (23)의 결과에서는 t = 0인 형태인데 어째서 이렇게 되는 것인지 잘 모르겠습니다.
Dm 함수를 한 주기에 대해 적분한다면 2pi가 나오게 된다는 점은 알고 있지만 위 식에서는 Dm에 f(t-k)가 붙어 있으니 t의 값에 따라 적분 결과가 다르게 될 것 같은데 어째서 t는 고려하지 않아도 되는지 잘 모르겠습니다.
주기 함수 $f(t), D_M(t)$는 모두 주기가 $2 \pi$입니다. 그래서 적분의 시작점을 어디로 잡든지 $2 \pi$만큼만 적분하면 결과는 모두 동일합니다.
삭제감사합니다. 곰곰히 생각해 보니 이해가 되는 듯 하네요. f(t-k)가 (t-k)에 관한 함수이기는 하지만 여기서 t는 적분과 관계없는 변수이므로 적분기호 안의 f(t-k)*Dm(k)의 값은 오로지 k에 의해서만 결정되는 건데 적분기호 안의 t와 범위에 쓰인 t를 동일하게 생각했네요.
삭제그리고 Dm 함수의 우함수 특성에 의해 Dm(t) = Dm(-t)이므로 Dm 함수는 y축 대칭이고, t'가 0일 때 f(t-t')과 f(t+t')의 값이 같으므로 첫째식과 둘째식의 차이는 함수 f를 y축으로 대칭시켜 적분한 것 뿐이네요. 그래서 첫째식과 둘째식의 결과가 같은 거군요.
삭제푸리에 급수가 균등 수렴함을 보이는 것을 M-판정법으로 한다고 하셨는데, 계수들의 수열이 절대수렴함을 어떻게 보일 수 있을까요? x=0을 대입하여 함수값에 수렴함을 이용할 수 있다고 생각했는데, 절대수렴이 아니라서 안되네요.
답글삭제그리고 역사 부분은 어떤 곳에서 찾아보시는지 여쭤봐도 될까요?
삭제1. 푸리에 급수의 균등 수렴성은 아래 링크에 소개되어 있어요. 푸리에 계수의 절대 수렴은 증명하는 게 아니고, 균등 수렴의 조건입니다.
삭제https://ghebook.blogspot.com/2020/06/uniform-convergence.html
2. 역사 부분은 위키피디아를 가끔 보기도 하고요, 논문이나 잡지를 읽다가 기억하고 싶은 걸 블로그에 적어놓고 있어요.
영상처리로 배우는 푸리에변환:
답글삭제https://www.aladin.co.kr/shop/wproduct.aspx?ItemId=309060931
추천합니다.
목차만 봐도 책이 재미있어 보이네요 ^^
삭제