천장에 매달린 사슬의 운동 방정식(Equation of Motion for Hanging Chain)

[경고] 아래 글을 읽지 않고 "천장에 매달린 사슬의 운동 방정식"을 보면 바보로 느껴질 수 있습니다.
1. 미분 방정식의 의미
2. 뉴턴의 운동 법칙
3. 줄에 대한 파동 방정식
4. 단진자의 운동 방정식

대가(大家, maestro)라는 사람들의 특징중 하나는 누구보다 먼저 고민하고 생각하기이다. 1732년베르누이 32세, 조선 영조 시절 다니엘 베르누이Daniel Bernoulli(1700–1782)는 [그림 1]과 같은 문제를 고민하여 답을 얻었다. 우리 관점에서 1732년은 조선(朝鮮) 영조(英祖) 8년에 해당한다. 조선 영조 시대에 사슬의 움직임을 고민하는 학자를 상상하기 어렵지만, 유럽에는 베르누이라는 수학자 겸 물리학자가 있었다. 시대를 새롭게 만드는 사람들은 거장이기 때문에, 그들에게 항상 찬사를 보내야 한다.

[그림 1] 늘어뜨린 사슬(출처: wikipedia.org)

천장에 사슬을 매달아 진동을 주면 그 사슬[1]은 어떻게 움직일까? 우리의 시작점은 줄에 대한 파동 방정식(wave equation for a string)이 되어야 한다.

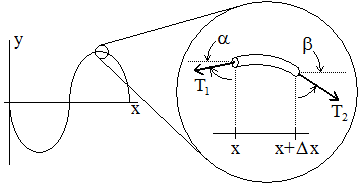
[그림 2] 줄에 생기는 파동(출처: wikipedia.org)

[그림 2]의 줄에 생기는 $y$방향 장력(tension), 질량(mass), 위치(position)의 관계식은 아래와 같다. 자세한 유도는 줄에 대한 파동 방정식(wave equation for a string)에서 볼 수 있다.

                       (1)

파동 방정식(wave equation)에서는 외부 힘이 없기 때문에, $x$방향 장력 $T_x$는 $x$에 대해 상수라고 가정했다. 하지만 [그림 1]과 같은 구조에서는 중력 때문에 $x$방향 장력의 변화를 다음처럼 고려해야 한다.

                       (2)

식 (2)를 식 (1)에 대입하면 [그림 1]에 대한 운동 방정식(equation of motion)을 얻을 수 있다.

                       (3)

사슬에 작용하는 $x$방향 장력을 구하기 위해 [그림 3]을 보자.

[그림 3] 천장에 매달린 사슬

천장에 매달려 있기 때문에 중력(gravity)이 아래 방향[혹은 $-x$방향]으로 작용하여 $x$방향 장력이 위치별로 일정하지 않게 된다. 따라서, 다음 관계식이 성립한다.

                       (4)

여기서 $g$는 중력 가속도(gravitational acceleration)이다. 만약 $x = 0$이면 장력이 0이지만, $x$가 증가하는 방향으로 가면 질량이 늘어서 장력이 점점 커진다. [그림 3]에서 천장 부근까지 올라가면, 장력에 기여하는 사슬의 질량이 최대가 된다. 따라서 중력에 의해 천장점의 장력이 최대이다. 다음으로 식 (4)를 식 (3)에 대입해 정리하면 다음 미분 방정식(differential equation)을 얻는다.

                       (5)

식 (5)를  편하게 풀기 위해 페이저(phasor)를 가정해 시간 변화 성분을 없애자. 그러면 다음과 같은 미분 방정식을 유도할 수 있다.

                       (6)

이 미분 방정식이 최초의 베셀 미분 방정식(Bessel's differential equation)이다. 베셀의 미분 방정식은 아래처럼 표현된다.

                      (7)

식 (7)에서 $n = 0$을 대입하면 식 (6)과 (7)이 매우 닮았음을 볼 수 있다. 따라서 다음과 같은 변수 치환을 하자[1].

                      (8)

여기서 $a$는 결정해야할 상수이다. 다음으로 식 (8)을 식 (6)에 대입하여 식 (7)과 비교하자.

                      (9)

식 (9)에 의하면 식 (6)은 분명 0차 베셀 미분 방정식이며, $y$의 변동은 0차 베셀 함수(the zeroth Bessel function)로 주어진다.

                      (10)


[참고문헌]

[1] C. Byrne, Notes on Bessel's Equation and the Gamma Function, University of Massachusetts Lowell, April 2009.

[다음 읽을거리]
1. 베셀의 미분 방정식