커패시터(Capacitor)

[경고] 아래 글을 읽지 않고 "커패시터"를 보면 바보로 느껴질 수 있습니다.

1. 전압

2. 전류

3. 저항

[수치 해석: 커패시터(출처: phet.colorado.edu)]

저항(resistor), 인덕터(inductor)와 더불어 회로 이론(circuit theory)을 구성하는 3대 소자인 커패시터(capacitor)는 전기(電氣, electricity)를 저장할 수 있는 소자이다. 커패시터라는 이름에서도 알 수 있듯이 이는 무언가를 수용할 수 있는 장치라는 뜻이다.[축전기(蓄電器)라고도 부르지만, 배터리(battery)란 의미가 너무 강해서 회로 이론에 쓰면 전압원과 헷갈릴 수 있다. 콘덴서(condenser)라는 이름도 붙이지만, 전기 분야가 발견되던 초기 이름이라 너무 구식이다. 그래서 현재는 커패시터란 용어로 거의 통일되었다.] 커패시터에 저장하는 물질은 당연히 전기의 원천인 전하(electric charge)이다.

[그림 1] 커패시터의 구조(출처: wikipedia.org)

커패시터가 전기를 저장하는 원리는 쿨롱의 법칙(Coulomb's law)이다. 우리가 잘 알듯이 ($+$)와 ($-$) 전하(電荷, electric charge)는 항상 서로를 당기기 때문에 [그림 1]과 같은 구성을 하면 전기를 모을 수 있다. 즉, 왼편 금속에 ($+$)를, 오른편 금속에 ($-$)를 강제로 놓으면 서로 당기기 때문에 전기가 모여있을 수 있다. 정확하게는 전기장(electric field)의 형태로 커패시터 내부에 모여있게 된다. 쉽게 생각하면 내부에 ($+$)와 ($-$) 전하를 많이 저장할 수 있는 장치를 커패시터라고 한다. 얼마나 많이 모이는가는 전기 용량(電氣容量, capacitance) 혹은 정전 용량(靜電容量)으로 계량한다. 전기 용량이 높으면, 동일한 전압을 가해도 더 많은 전하가 모인다. [그림 1]을  보면 왼쪽 금속판에 ($+$) 전하가 모여있다. 이 경우는 쿨롱 법칙(Coulomb's law)에 의해 ($+$) 전하끼리 서로 미는 힘(척력)이 생기기 때문에 ($+$) 전하를 왼쪽 금속판에 모으기 힘들다. 즉, 금속판에 ($+$) 전하를 모아 놓으면 서로 밀기 때문에 금속판을 빠져 나오려는 힘이 생긴다.[∴ ($+$) 전하가 금속판을 나올 수 없도록 외부에서 ($+$) 전압(voltage)을 걸어준다.] 이런 ($+$) 전하 사이의 척력을 이기고 금속판에 ($+$) 전하를 모으기 위해 반대편 금속판에 ($-$) 전하가 있다. 쿨롱 법칙(Coulomb's law)에 의해 ($+$)와 ($-$) 전하는 서로 강하게 당기는 힘[인력]이 생겨 ($+$) 전하는 왼쪽 금속판에 저장될 수 있다. 더 많은 전하를 모으려면 전기장이 커져야 하므로 [그림 1]의 금속판의 간격 $d$는 작아질수록 좋다. 또한, ($+$) 전하간의 척력을 줄이려면 금속판 자체의 공간이 넓어져야 하므로 금속판의 면적 $A$가 커져야 많은 ($+$) 전하를 금속판에 모을 수 있다. 마찬가지 논증이 ($-$) 전하에 대해서도 성립한다.

[그림 1]과 같이 전하가 충전된 커패시터에 저항을 연결하면 충전된 전하가 방전되면서 저항에 일을 시킬 수 있다. 이런 일을 내가 원하는 방식대로 설계하기가 회로 이론의 존재 목적이다. 커패시터의 특성을 보여주는 중요 공식은 아래에 있다.

                       (1a)

                       (1b)

여기서 $Q$는 전하, $V$는 전압(voltage), $C$는 전기 용량(capacitance) 혹은 영어 발음 그대로 커패시턴스라고 부른다. 전기 용량의 단위는 F[패럿 혹은 패러드, farad]이다. 패럿이라는 이름은 전속 밀도(electric flux density) 개념을 실험적으로 증명한 패러데이Michael Faraday(1791–1867)로부터 왔다. 패러데이는 구형 커패시터(concentric spherical capacitor)를 제작하여 이  커패시터에 전하를 충전시킨 후 커패시터 내부의 유전 물질을 다양하게 바꾸면서 충전된 전하의 변화를 측정했다. 이 실험에서 놀라운 결과가 얻어졌다. 구형 커패시터가 개방되었다면 내부 유전 물질의 종류에 관계없이 커패시터에 충전된 전하량[혹은 전속 밀도]은 전혀 변함이 없었다. 즉, 전속 밀도는 유전 물질의 종류와는 관계 없는 양이다.

흔하지는 않지만 전기 용량 $C$의 역수를 탄성 비율로 번역하는 일래스턴스(elastance) $S$라고도 한다. 전하를 저장하는 커패시터와 탄성력을 가진 스프링(spring)은 전혀 관계없는 소자이지만, 일래스턴스의 제안자인 헤비사이드Oliver Heaviside(1850–1925)의 논리를 따라가보면 고개가 끄덕여진다. 또한 로렌츠 진동자 모형(Lorentz oscillator model)에서 스프링처럼 운동하는 전자(electron)의 탄성 특성은 일래스턴스로 정확히 대체된다.
식 (1b)는 식 (1a)의 시간 미분형이다. 회로 이론에서는 식 (1b)를 많이 쓴다. 전압을 미분한 부분은 전류에 정비례하므로 전압이 순식간에 변하기는 불가능하다.[∵ 전압이 불연속이 되면 전류는 무한대가 되어야 한다.] 이 개념을 물리적으로 이해하려면 전하 보존의 법칙(conservation of electric charge)을 생각해야 한다. 전하는 갑자기 생기거나 사라지지 않으므로 커패시터에 충전된 전하도 갑자기 사라지거나 생길 수 없다. 전하량이 변동될 때는 전류가 흐를 때 뿐이다. 또한, 전하가 존재하면 전압이 있으므로 커패시터의 전압은 갑자기 생기거나 사라질 수 없다. 이게 커패시터의 중요한 특징이 된다. 식 (1)과 같은 공식을 보면 무턱대고 외우려고 하지 말자. 정말 식 (1)이 맞는지 의심을 하고 그 다음에 확신을 가져야 한다. 우리 기준으로 완벽히 증명되지 않으면 절대로 믿지 않는 독한 마음이 우리를 연구자로 만든다.

[전기 용량의 관계식]

전압($V$)을 높이면 충전되는 전하($Q$)는 선형적으로 증가한다. 이때의 비례 상수가 전기 용량($C$)이다.

[증명]

식 (1a)의 증명을 위해 먼저 전기장(electric field)–전속 밀도(electric flux density) 관계식을 생각한다.

                       (2)

전체적인 증명 방법은 옴의 법칙(Ohm's law) 증명과 매우 유사하다. 식 (2)를 면적 적분해서 전하를 먼저 뽑아낸다.

                       (3)

여기서 면적 적분은 전속 밀도를 임의 표면적 $s$에 대해 적분하여 전하 $Q$를 만든다. 이 면적 적분은 일반적으로 닫힌 면적 적분으로 표기해야 하나 옴의 법칙 증명과 유사하게 만들기 위해 식 (3)처럼 표기한다. 전속 밀도 $\bar D$와 면적 미분소 $d \bar a$는 같은 방향으로 잡아서[∵ 전속 밀도가 뚫고 지나가는 단면적은 임의로 잡을 수 있다.] 벡터를 사용하지 않고 스칼라를 사용한다.[∵ 내적을 구성하는 벡터가 같은 방향이면 두 벡터 크기의 곱으로 생각할 수 있다.] 전압과 전기장의 관계로부터 식 (4)가 정의된다.

                          (4)

여기서도 전기장 $\bar E$의 방향과 선 미분소 $d \bar l$의 방향을 동일하게 잡았다.[∵ 전기장을 정의하는 선 미분소의 방향은 임의로 잡을 수 있다.] 그래서 전속 밀도, 전기장, 면적 미분소, 선 미분소는 동일한 벡터 방향을 가진다. 식 (4)를 식 (3)에 대입하여 정리한다.

                          (5)

여기서 전압 미분소 $dV$가 적분을 빠져나오는 이유는 옴의 법칙 증명과 동일하다. 즉, 표면적 $s$ 상에서 전압 $V$는 상수이고, $dl$을 잘 정의하여 $dV$가 표면적에 대해 상수가 되도록 한다. 다음으로 식 (5)를 선 적분하면 식 (1a)를 증명할 수 있다.

                          (6)

여기서 $Q$가 적분 구간 바깥으로 나올 수 있는 이유는 선 적분 구간에 대해 $Q$는 상수이기 때문이다.[∵ 가우스 정리(Gauss' theorem)에 의해 특정 표면적을 둘러싸는 면적 적분 내부에 있는 전하만이 전체 전하량을 결정한다.]

______________________________

식 (1a)는 단순 정의라고 생각하기 쉬운데 전기장–전속 밀도 관계를 이용하면 위와 같이 증명이 된다. 전자기학 공부에서 이런 과정 자체는 상당히 재미있다. 증명이 명확히 되기 때문에 안심하고 식 (1a)를 사용할 수 있다.

[그림 2] 평행판 커패시터(출처: wikipedia.org)

식 (6)의 전기 용량 공식은 일반적이기 때문에 어떠한 구조에도 사용할 수 있다. 예를 들어 [그림 2]에 있는 무한 평행판(infinite parallel-plate)의 전기 용량을 식 (6)을 이용해 계산한다. 전기장 방향이 $z$축이라면 다음을 얻는다.

                          (7)

만약 평행판이 유한하다면 평행판의 끝단에 전하가 몰려 전기장이 강해지기 때문에 식 (7)보다는 전기 용량이 커진다. 경험적으로 유한 평행판의 전기 용량은 식 (7)보다 10~15 % 정도 커진다. 모서리 효과(edge effect)를 고려한 전기 용량의 정확한 계산을 원하면 [여기]를 참고할 수 있다. 식 (1a)를 이용하여 전기 용량을 아래와 같이 정의할 수도 있다.

                             (8)

전기 용량을 정의한 동일한 구조에 전류가 흐를 수 있다면 다음 저항 관계식이 자연스럽게 성립한다.

                          (9)

유전율(誘電率, permittivity) $\epsilon$과 전도도(傳導度, conductivity) $\sigma$가 전체 공간에 대해 일정하다면 다음 관계식이 항상 성립해야 한다.

                         (10)

신기하게도 저항($R$)과 전기 용량($C$)의 곱은 유전체의 이완 시간(relaxation time)이 된다. 식 (10)의 이완 시간 $\tau$는 전하 밀도(혹은 전하)가 존재하는 평균 시간(시간의 기대값)이다.

[그림 3] 키르히호프 전류 법칙(출처: wikipedia.org)

이상의 논의를 통해 직류(DC: Direct Current)에서 정의된 KCL(Kirchhoff Current Law)을 교류(AC: Alternating Current)로 확장할 수 있다. 전하 보존 법칙(conservation of electric charge)을 체적 적분하고 가우스 정리(Gauss' theorem)와 식 (1a)를 적용하면 다음을 얻는다.

                         (11)

원칙적으로 AC에서는 KCL이 성립하지 않는다. 하지만, 식 (11)과 같이 커패시터에 흐르는 전류를 변위 전류(變位電流, displacement current)로 정의해서 식 (11)의 마지막식으로 정리하면 AC에서도 KCL이 성립하도록 만들 수 있다. 이상을 바탕으로 병렬(竝列, parallel or shunt)과 직렬(直列, series)에 대한 전기 용량 공식을 증명한다.

[병렬로 된 커패시터]

[그림 4] 병렬로 된 커패시터(출처: wikipedia.org)

                         (12)

[증명]

[그림 4]는 병렬 구성이므로 전기적 높이인 전압은 KVL(Kirchhoff Voltage Law)에 의해 어느 커패시터에서나 같다. 이 전압을 $V$라 놓는다. 그러면 식 (1a)를 미분하여 식 (1b)처럼 각 커패시터[$C_1, C_2, \cdots, C_N$]에 흐르는 전류[$I_1, I_2, \cdots, I_N$]를 정의할 수 있다. 마지막으로 식 (11)의 일반화된 KCL을 이용하여 전체 전류 $I$를 계산한다.

                         (13)

______________________________

[직렬로 된 커패시터]

[그림 5] 직렬로 된 커패시터(출처: wikipedia.org)

                         (14)

[증명]

[그림 5]는 직렬 회로이므로 식 (11)의 일반화된 KCL(Kirchhoff Current Law)에 의해 각 커패시터에 흐르는 전류는 같다. 이 전류를 $I$라 설정한다. 그러면 식 (1a)의 미분에 의해 식 (1b)처럼 각 커패시터[$C_1, C_2, \cdots, C_N$]에 걸리는 전압[$V_1, V_2, \cdots, V_N$]의 미분을 정의할 수 있다. 다음으로 KVL(Kirchhoff Voltage Law)을 이용하여 전체 전압 $V$의 미분을 계산하면 다음과 같다.

                         (15)
______________________________

[그림 6] 실제 커패시터 모습(출처: wikipedia.org)

[그림 6]은 실제로 사용되는 커패시터를 보여준다. 크기도 다양하며 커패시터를 만들 때 사용한 유전체(誘電體, dielectric)의 종류도 많다. 식 (7)에 한 유도처럼 유전율이 커질수록 유전 물질의 두께가 얇을수록 전기 용량은 커진다. 따라서 전기 용량을 결정은 주로 커패시터 내부에 있는 유전 물질이다. [그림 6]처럼 커패시터의 종류는 많지만 커패시터 내부를 채우는 물질에 따라 구분하면 크게 세라믹 커패시터(陶磁器, ceramic capacitor)와 전해 커패시터(電解, electrolytic capacitor)[1]로 나눌 수 있다. 세라믹 커패시터는 도자기의 재료인 고체 세라믹(도자기, 陶磁器, ceramic)을 내부에 채우기 때문에 유전체의 두께가 두꺼워져(보통 5 μm) 전기 용량을 키우기가 어렵다.[비유전율은 보통 10 정도이나 사용하는 분말 종류에 따라 1000 이상이 되게 할 수도 있다.] 반면, 액체 전해질이 두 극 사이에 채워진 전해 커패시터는 아주 얇은 산화막[보통 1 nm/V: 1 V를 가할 때 1 nm 정도 형성]을 만들 수 있어 전기 용량을 현저하게 높일 수 있다.[전해질의 일종인 소금물은 분극(分極, polarization)이 너무 잘 되어 전기를 흘릴 수도 있다. 소금물의 비유전율은 대충 100 정도이며 산화막의 비유전율은 10 정도이다.]

[그림 7] 전해 커패시터의 다양한 크기(출처: wikipedia.org)

전해 커패시터[1]는 세라믹 커패시터보다 전기 용량이 크지만 불편하게도 대부분 극성(極性, polarity)을 가진다. 즉, 전해 커패시터는 직류 전압을 기준으로 ($+$)와 ($-$)를 연결하는 부분이 정해져 있다. 이런 특성은 상당히 재미있다. 왜냐하면 [그림 1]의 커패시터 구조는 원래 극성 구별이 없기 때문이다.

[그림 8] 전해 커패시터의 동작원리

왜 이렇게 극성을 구별해주어야 할까? 이 부분을 이해하려면 먼저 [그림 8]에 제시한 전해 커패시터의 동작 원리를 이해해야 한다. 전해 커패시터를 제작할 때 양극(anode)과 음극(cathode)에 쓰이는 금속은 가격이 저렴한 알루미늄[그림 8의 노란색]을 주로 쓴다. 양극과 음극의 단면적이 넓어져야 많은 전하를 저장할 수 있으므로 먼저 에칭(etching) 공정을 이용해 실효 면적을 늘린다. [그림 8]처럼 양극에 두꺼운 산화막[그림 8의 하늘색]이 형성되므로 양극을 많이 에칭해서 단면적이 커지도록 한다. 다음에 특수 전해질에 담근 양극에만 강한 전압을 가해서 양극에만 두꺼운 산화막을 인공적으로 형성(forming)시킨다. 이를 위해 보통 음극 알루미늄보다 양극 알루미늄을 두껍게 만든다. 그 다음에 전해질을 머금은 종이[그림 8의 보라색]를 양극과 음극 사이에 넣고 둘둘 말아 전해 커패시터를 최종적으로 만든다. 음극은 인위적으로 산화시키지는 않았지만 공기 중에 있는 산소에 의해 음극은 자연적으로 얇은 산화막이 생긴다. 그러면 [그림 8]과 같은 전해 커패시터가 얻어진다. 사실 전해 커패시터는 양극($C_a$)과 음극($C_c$) 커패시터가 직렬로 연결된 구조이나 $C_c \gg C_a$이므로[∵ 조건은 같은데 음극쪽 산화막 두께가 매우 얇다.] 식 (14)를 이용하면 아래가 성립한다.

                         (16)

전해 커패시터가 세라믹 커패시터보다 전기 용량이 큰 이유도 [그림 8]을 보면 분명해진다. 원래 두께($d_{\rm old}$)보다 산화막 두께($d_{\rm new}$)가 매우 얇기 때문에 식 (7)에 의해 전해 커패시터의 전기 용량이 월등하게 커진다. 정상적인 극성으로 DC 전압을 가하면 전해질을 통해 DC 전류가 흐르게 되고 이 전류가 양극(anode) 금속에 산화막을 지속적으로 형성한다. 산화막이 어느 정도 형성되면 DC 전류를 차단하게 되어 커패시터로 동작하게 된다.[∵ 산화막은 절연체이기 때문에 DC 전류를 흘리지 않는다. 하지만 절연 파괴 전기장(breakdown electric field)을 넘어서게 되면 전류가 흐를 수 있다.] 여러 가지 이유로 산화막이 얇아질 수 있으므로 산화막을 재형성하기 위해 계속적으로 전해 커패시터에는 누설 전류가 생기게 된다. 따라서, 전해 커패시터는 세라믹 커패시터보다 손실이 매우 크다. 음극(cathode) 금속에는 전압이 반대 극성으로 걸렸기 때문에 산화막을 없애는 방향으로 화학 작용이 일어나지만 양극에 있는 산화막이 전류를 차단하기 때문에 음극 산화막이 완전히 없어질 수는 없다.

[전해 커패시터의 폭발 시연]

원래 정해진 극성과 반대로 DC 전압을 가해주면 양극에 원래 존재하던 산화막을 없애는 방향으로 화학 작용이 일어나서 결국에 커패시터는 단락(短絡, short)과 비슷한 동작을 하므로[커패시터는 원래 개방(開放, open) 특성을 가져야 한다.] 극성을 잘못 연결한 경우는 열에 의해 전해 커패시터가 폭발하게 된다. 따라서, 사용할 때 전해 커패시터의 극성을 꼼꼼하게 확인해야 한다. 이런 특성을 제대로 이해하려면 알루미늄[금속]과 전해질에서 생기는 화학 작용을 알아야 한다.

      (17)

식 (17)은 알루미늄($\rm Al$)과 물($\rm H_20$)이 반응하면 산화막($\rm Al_2O_3$)과 수소 기체($\rm H_2$)가 생김을 의미한다. 식 (17)과 같은 반응이 일어나려면 전도 전류(conduction current)가 아닌 이온 전류(ionic current: 이온(ion)이 움직여서 만드는 전류)가 흘러야 한다. 이때 DC 전압이 필요하다. 정상적인 극성인 ($+$) 전압을 알루미늄 양극(anode)에 가하면 알루미늄($\rm Al$)과 산화 이온(oxide ion: ${\rm O^{2-}}$)이 반응해서 산화막($\rm Al_2O_3$)과 전자($e$)를 만든다. 왜냐하면 ($+$) 전극에서 강하게 ($-$)인 산화 이온을 당기기 때문이다. 또한, 산화막 근처에 존재하는 알루미늄 이온($\rm Al^{3+}$)은 ($-$) 전압 쪽으로 이동하면서 물과 반응해서 산화막($\rm Al_2O_3$)과 수소 이온($\rm H^+$)을 만든다. 혹은 알루미늄과 전해질이 직접 반응해서 알루미늄 이온과 전자를 만들 수도 있다. 이렇게 만들어진 알루미늄 이온은 전기장에 의해 ($-$) 전압쪽으로 움직인다. 하지만 물과 만나면 식 (17)의 넷째 줄처럼 반응한다. 최종적으로 ($-$) 전압이 걸린 음극(cathode)으로 이동한 수소 이온은 전자와 만나 수소 기체가 된다. 하지만 이런 산화막을 유지하기 위한 과정은 어느 정도 진행이 되면 전기장(electric field)이 약해져[∵ 전압이 고정된 상태에서 산화막이 두꺼워지기 때문에] 이온 전류가 흐를 수 없기 때문에 더 이상 진행되지 않는다. 반대 극성으로 ($-$) 전압을 알루미늄 양극에 걸면 식 (17)과는 반대 현상이 생긴다. 산화막이 전해질과 반응해서 알루미늄과 물을 만들게 된다. 알루미늄 음극에는 ($+$) 전압이 걸려있기 때문에 음극에 산화막이 약간 생기지만 양극에 있던 산화막이 파괴되어 이미 막대한 전류가 커패시터 내부에 흐르는 상태이기 때문에 전해 커패시터는 이 열을 이기지 못하고 파괴되어 버린다. 이 경우 [그림 8]과 같이 자연적으로 음극에 커패시터($C_c$)가 존재하기 때문에 DC 전류가 흐를 수 없을 것 같다. 하지만 음극 산화막은 매우 얇기 때문에 절연 파괴 전기장을 쉽게 넘어서므로, 음극 산화막을 통해 DC 전류가 흘러 전해 커패시터를 파괴할 수 있다.

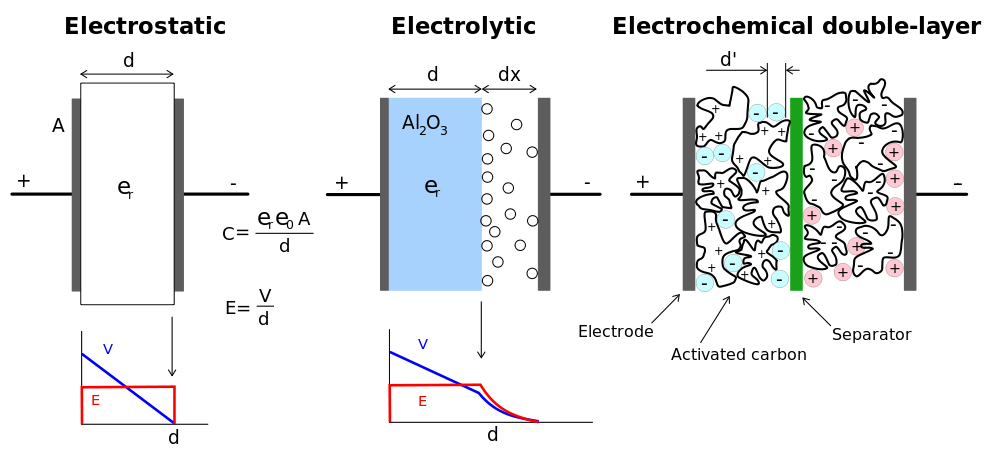
[그림 9] 커패시터의 원리 비교(출처: wikipedia.org)

전해 커패시터보다 더욱 에너지를 잘 저장할 수 있는 소자는 초강력 커패시터(supercapacitor or ultracapacitor)[2], [3]이다. 초강력이라는 의미는 다른 어떤 커패시터보다 전기 용량이 크다는 뜻이다. 초강력 커패시터는 보통 3000 F 정도의 전기 용량을 가지며 5.5만원[$\approx$ $50] 정도 주면 구입할 수 있다. 전기 용량이 매우 크기 때문에 태양 전지와 같은 에너지원의 간편 저장 장치로 사용될 수 있다.

[초강력 커패시터(supercapacitor)의 위력]

초강력 커패시터가 매우 큰 전기 용량을 가질 수 있는 원리는 전기 이중층(EDL: Electric Double-Layer)이다. [그림 9]를 보면 분리막(separator)을 사이에 두고 형성된 전기 이중층을 볼 수 있다. 물론 전하가 이동해야 하기 때문에 활성층(active layer: 전하가 저장되는 층)과 분리막은 전해질에 담겨있어야 한다. 즉, 식 (7)에 제시하듯 구멍이 많은 활성탄을 사용해 면적($A$)을 증가시키고 전기 이중층의 두께[$d$: 보통 수 Å]를 매우 좁게 한 커패시터가 초강력 커패시터이다.

[그림 10] 세라믹 커패시터의 전기 용량 표시법(출처: wikipedia.org)

[그림 10]은 세라믹 커패시터의 전기 용량을 표시하는 방법의 예시를 보여준다. 전기 용량의 기준 단위는 F로 매우 크기 때문에, 세라믹 커패시터의 상용 단위로 적절하지 않다. 그래서 통상적인 세라믹 커패시터의 상용 단위는 pF을 사용한다. 예를 들어, [그림 10]처럼 473이 세라믹 커패시터에 쓰여져 있으면, 전기 용량을 473 = $47 \times 10^3$ pF = $47$ nF만큼 가진 커패시터가 된다.

[참고문헌]

[1] P. M. Deeley and the FaradNet Staff, Electrolytic Capacitors: Theory, Construction, Characteristics and Applications, 2nd ed, 1938.

[2] 김영호, "커패시터와 배터리의 가교 장치, 울트라커패시터," EP&C, pp. 44–50, 2002년 8월.

[3] R. Kötz and M. Carlen, "Principles and applications of electrochemical capacitors," Electrochimica Acta, vol. 45, no. 15–16, pp. 2483–2498, May 2000.

[4] I. Smolić and B. Klajn, "Capacitance matrix revisited," Prog. Electromagn. Res. B, vol. 92, pp. 1–18, 2021.

[5] A. M. Thompson and D. G. Lampard, "A new theorem in electrostatics and its application to calculable standards of capacitance," Nature, vol. 177, p. 888, May 1956.

[6] D. G. Lampard, "A new theorem in electrostatics with applications to calculable standards of capacitance," Proc. IEE - Part C: Monographs, vol. 104, no. 6, pp. 271–280, Sep. 1957.

[다음 읽을거리]

1. 전기장의 에너지

2. 인덕터

3. 페이저를 이용한 임피던스 정의

4. 유전 상수 재는 방법

5. 가장 쉬운 안테나 이론

6. 평행판 커패시터