1. 전기장
2. 전압
전기장(electric field)의 관계식을 유도할 때는 단 하나의 전하(electric charge)만을 고려한다. [그림 1]처럼 두 개의 서로 다른 전하를 고려하면 어떻게 될까?

[그림 1] 전기 쌍극자
[그림 1]의 전하 분포는 매우 중요하다. 왜냐하면 일반적인 물질에 전기장을 가하면 [그림 1]과 같이 전하가 서로 분리되기 때문이다.[∵ 전기장이 가해지면 ($+$) 전하는 ($-$)쪽으로, ($-$) 전하는 ($+$)쪽으로 움직이기 때문이다.] 전기장에 의해 전하가 분리되는 현상은 분극 혹은 극갈림(分極, polarization)이라 한다. 식 (1)에 있는 전압(voltage)의 정의를 이용해 [그림 1]의 전기 쌍극자(electric dipole) 특성을 식 (2)와 같이 계산한다.
 (1)
(1) (2)
(2)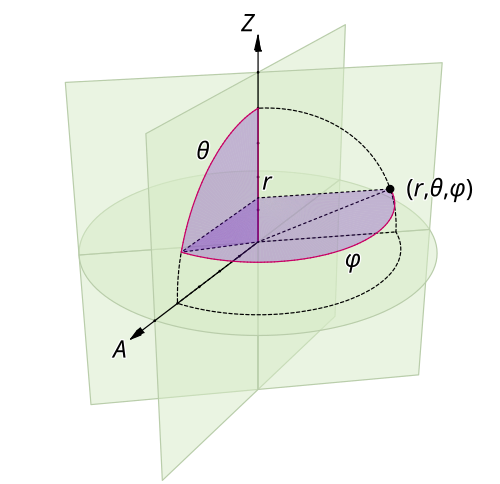

[그림 2] 구 좌표계의 표현(출처: wikipedia.org)
원점 기준에 대한 관측점(observation point) $r$이 매우 멀리 있다고 하면[$r \gg d$] 식 (2)를 아래처럼 근사화할 수 있다.
 (3)
(3)
여기서 $r^2$ = $\rho^2 + z^2$, $\rho^2$ = $x^2 + y^2$; $\theta$는 [그림 2]에 제시한 극고도각(極高度角, polar angle: $\theta$는 꼭대기부터 시작해 내려오기 때문에 일반 고도각과는 정의가 약간 다름), $\hat z \cdot \hat r$ = $\cos \theta$, 벡터 $\bar d$ = $d \hat z$는 변위 벡터(displacement vector)이다.

[그림 3] 전기 쌍극자 모멘트의 방향(출처: wikipedia.org)
[그림 1]에서 변위 벡터의 정의를 보면 특이하다. [그림 3]처럼 ($-$) 전하에서 ($+$) 전하로 가는 방향이 벡터 $\bar d$의 기준 방향이 된다. 이 방향은 전기장을 정의할 때와는 반대이다.[∵ 전기장은 ($+$) 전하에서 나와 ($-$) 전하로 들어간다.] 식 (3)에 있는 전기 쌍극자 모멘트 혹은 전기 쌍극자 능률(electric dipole moment) $\bar p$의 기준 방향을 [그림 3]과 같이 전기장과 반대로 정하면, 유전체(dielectric)의 성질을 표현하기가 매우 편리하다.

[그림 4] 외부 전기장과 분극에 의한 전기장의 방향(출처: wikipedia.org)
왜냐하면 [그림 4]처럼 물체에 전기장이 가해지면 전기적인 인력과 척력에 따라 물체 내부에 ($+$)와 ($-$) 전하가 나누어지는 분극이 생기고, 분극에 의한 전기장은 외부 전기장과 정확히 반대가 되기 때문이다. 즉, 분극에 의한 전기장과는 반대 방향으로 물체 내부의 전기 쌍극자 모멘트를 정의하면, 외부 전기장과 전기 쌍극자 모멘트의 벡터 방향이 일치해서 유전체의 공식화가 간단해진다. 전기 쌍극자 모멘트(electric dipole moment)에 나오는 모멘트 혹은 능률(能率, moment)은 어떤 물리량이 변하는 경향을 뜻한다.[영어 moment의 어원이 라틴어 momentum(운동)인 이유이다.] 식 (3)은 전기 쌍극자가 변하는 경향을 나타내는 지표라서 당연히 모멘트가 어울린다. 조금 더 전문적으로 설명하면 모멘트는 어떤 형태나 특성을 곱 형태로 표현하는 핵심 측정량(measure)을 뜻한다. 물리학에서는 주로 수직 길이를 모멘트라 하지만 반드시 이럴 필요는 없다. 식 (3)에서는 길이와 더불어 전하량까지 곱한 값을 모멘트로 정의한다.
식 (3)에 구배 연산자(gradient operator)를 적용해서 전기장을 계산한다.
 (4)
(4) (5)
(5) 그런데 식 (5)가 성립하는 영역은 $r \gg d$이므로 전기 쌍극자가 있는 곳[$r \approx d$]과는 거리가 매우 먼 곳이다.

[그림 5] 전기 쌍극자가 만드는 전기장(출처: wikipedia.org)
전기 쌍극자 가까이에서는 식 (5)가 맞지 않으므로 $d \gg r$이라 가정하고 식 (3)의 방법론을 적용한다.
 (6)
(6)
식 (6)에 구배 연산자를 적용하면 전기 쌍극자 가까이의 전기장을 구할 수 있다.
 (7)
(7)
만약 $d$가 매우 작아지면 어떻게 되는가? 편하게 계산하기 위해 전기 쌍극자 모멘트 $\bar p$는 $d$에 관계없이 일정하고 $d$만 작아진다고 가정한다. 그러면 다음 극한이 성립한다.
 (8)
(8)여기서 반지름이 $d/2$인 구 부피의 극한은 $0$이라고 가정한다. 3차원 디랙 델타 함수(Dirac delta function) $\delta (\bar r)$는 아래처럼 정의한다.
 (9)
(9)여기서 $\bar r , \bar r'$는 각각 관측점(observation point)과 원천점(source point)이다.
[반도체에서 여기자(勵起子) 혹은 엑시톤(exciton)이 만드는 분극자(分極子) 혹은 폴라리톤(polariton)]
미시 세계에서 분극 현상을 설명하는 양자화된 준입자(quasiparticle)는 분극자, 폴라리톤, 혹은 극갈림알(分極子, polariton)이라 부른다. 분극자는 외부에서 입사하는 빛과 금속(metal)이나 반도체(semiconductor)에 존재하는 전기 혹은 자기 쌍극자(electric or magnetic dipole)의 강력한 상호 작용으로 발생한다. 예를 들어, 반도체에 빛을 비추면 어떤 경우에 여기자 분극자 혹은 엑시톤 폴라리톤(exciton polariton)이 생긴다. 이때 빛으로 생성한 회전하는 전자–정공 쌍(electron–hole pair, EHP)인 여기자 혹은 엑시톤(勵起子, exciton)이 전기 쌍극자를 담당한다. 시간이 지나면 EHP는 점점 감소하면서 사라져 빛이 다시 방출한다. 이 빛을 공진기(resonator)에서 반도체로 다시 되돌리면, EHP의 여기자가 다시 출현한다. 이 과정이 계속 반복되면서 빛과 여기자의 상호 작용은 하나의 입자처럼 행동해서 이 부분을 여기자 분극자라 명명한다.

(a) SPP의 전자기장 구성: $x$축으로 진행
(b) 진행 방향으로 전기장의 변화
[그림 6] 표면 플라즈몬 분극자(surface plasmon polariton, SPP)의 진행(출처: wikipedia.org)
금속과 유전체가 접합된 표면에는 [그림 6]처럼 플라즈몬(plasmon), 해리체자(解離體子), 혹은 플라즈마알[플라즈마 알갱이]이 존재할 수 있다. 다른 말로 덩어리 플라즈몬(bulk plasmon)이 아닌 표면 플라즈몬(surface plasmon)으로 정확히 부른다. 빛이 금속과 유전체 표면에 입사하면, 플라즈마(解離體, plasma)처럼 자유 전자(free electron)가 풍부한 금속 표면에 빛의 전기장이 유기하는 플라즈몬 혹은 더 쉽게 전하 밀도의 진동(oscillation of electric charge density)이 표면에 생긴다. 이 현상은 손실 유전체에 나타나는 침투 깊이(penetration depth)와 비슷하다. 그 다음에 빛의 주파수[주로 가시광(visible light) 대역]와 전기장(electric field)에 따라 전자가 모이거나 흩어지는 영역이 차례로 만들어져 분극자가 형성된다. 이로 인해 빛이 진행하는 방향으로 [그림 6]과 같이 표면 플라즈몬이 극성을 바꾸는 분극자인 표면 플라즈몬 분극자 혹은 폴라리톤(surface plasmon polariton, SPP)이 표면파(surface wave) 형태로 진행한다. 그래서 빛과 함께 ($+$)와 ($-$)로 교대 진동하는 전하 밀도(electric charge density)의 상호 작용을 준입자(quasiparticle)인 표면 플라즈몬 분극자로 이름 붙인다.

[그림 7] 전기 쌍극자에 작용하는 전기력
물질 내부에 고정된 전기 쌍극자에 작용하는 전기력은 [그림 7]과 같다. 외부에서 인가한 전기장 $\bar E$에 따라 전기 쌍극자의 ($+$)와 ($-$) 전하는 전기력을 받는다. 하지만 전기 쌍극자는 결정 분자의 내부에 있기 때문에 전기력이 있더라도 자유롭게 병진 운동을 할 수는 없다. 대신에 전기력에 의한 회전 운동이 다음처럼 발생할 수 있다.
 (10)
(10)따라서 회전력(torque) $\bar \tau$는 전기 쌍극자 모멘트 $\bar p$와 외부 전기장 $\bar E$의 벡터 외적과 같다. 즉, 전기 쌍극자 모멘트에 수직인 방향으로 입사하는 전기장이 전기 쌍극자의 회전을 발생시킬 수 있다.
 (11)
(11)식 (11)은 전자기파(electromagnetic wave)를 사용하는 전자레인지에서 물 분자를 회전시키는 원리이다. 시간적으로 변하는 전기장은 식 (11)에 따라 전기 쌍극자를 가진 물 분자의 회전을 일으키고, 공진 주파수에 해당하는 주기로 전기장이 변하면 물 분자가 완전히 회전을 해서 마찰에 의한 열을 발생시킨다. 식 (11)에 바탕으로 두고 전기 쌍극자가 가진 위치 에너지도 정의할 수 있다. 위치 에너지는 기준점과의 차이만 중요하기 때문에, 보통 회전력이 가장 큰 $\theta$ = $\pi/2$를 위치 에너지의 영점으로 삼는다. 따라서 $\theta$에서 전기 쌍극자가 가진 위치 에너지 $U$는 다음과 같이 정의한다.
 (12)
(12) (13)
(13)전기장 $\bar E$가 $\bar p$와 동일한 방향으로 가해지면, 위치 에너지가 가장 낮아져서 $\bar p$는 이 상태에 머물 수 있다. 또한 $\bar E$의 방향이 $\bar p$와 반대인 경우는 가장 높은 위치 에너지로 인해 $\bar p$가 불안정해진다.

[그림 8] 전기 단극자(electric monopole)로부터 전기 쌍극자, 4극자, 8극자를 생성
[그림 1]에 소개한 전기 쌍극자를 $z$방향으로 평행 이동해서 다양한 전기 다극자(electric multipole)를 생성할 수 있다. [그림 8]처럼 전기 쌍극자를 복사해서 $\pm z$방향으로 $d/2$만큼 평행 이동하고, $-z$방향으로 움직인 전기 쌍극자의 전하 부호를 바꾸면 전기 4극자(electric quadrupole)가 생긴다. 이 4극자를 다시 복사하고 $z$축에 대해 $\pm d/2$만큼 옮기고, 아래쪽 4극자의 전하 부호를 뒤집은 결과는 전기 8극자(electric octupole)로 부른다. 이와 같은 방식으로 2의 거듭제곱인 전기 다극자를 여러 가지로 만들 수 있다.
전기 4극자의 전압 관계식 $V_4(\bar r)$을 전기 쌍극자의 전압인 식 (3)으로부터 만들어본다.
 (14)
(14)여기서 $z$ = $r \cos \theta$; $V_2(\bar r)$은 전기 쌍극자의 전압이다. 식 (14)는 4극자의 전압이 $r^3$에 반비례하는 결과를 명확히 보이지만 약간 오차가 있는 점근식이다. 더 정확한 결과를 얻으려면 르장드르 함수(Legendre function)의 생성 함수(generating function)를 써서 [그림 8]에 보인 전기 4극자의 분포를 계산해야 한다.
 (15a)
(15a)[그림 8]과 같은 전기 다극자의 생성 방식으로 인해 전기 4극자는 단극자와 쌍극자에 해당하는 $n$ = $0$과 $1$ 항이 상쇄된다. 그래서 원점[그림 8에서 초록색] 기준으로 $\pm d$만큼 떨어진 $+Q$ 전하의 전개식에서 $n$ = $2$인 항만 선택한다.
 (15b)
(15b)식 (14)와 (15b)를 비교하면 $\sin^2 \theta$만큼 차이나며, 식 (15b)가 식 (14)보다 더 정확한 근사이다. 이와 비슷한 방법으로 전기 다극자의 전압식을 쉽게 유도할 수 있다. 다른 관점으로 르장드르 다항식(Legendre polynomial) $P_n(\cos \theta)$는 전하 개수가 $2^n$인 전기 다극자의 전압 계수에 정비례한다.
[1] J. D. Jackson, Classical Electrodynamics, 3rd ed., John Wiley & Sons, 1999.
[다음 읽을거리]
1. 유전체의 비밀
2. 자기 쌍극자 모멘트

R+ 와 R- 에 대한 식이 처음에 이해가 안됐습니다. 전자기학책을 펼쳐보니, r>>d 면 R+, R-, r 이 평행이 된다고 가정할 수가 있는거네요. 그래서 R+ 는 r 보다 d/2*cos(theta) 만큼 작고, R-는 r보다 d/2*cos(theta) 만큼 크다고 표현할 수 있네요. 혹시 이해안되신 분들은 참고 되시길 바랍니다.
답글삭제조언 감사합니다, 해리님. ^^
삭제아닙니다. 너무 기초적인 내용이라 다들 이해하실 것 같습니다만, 혹시나 해서 남겼습니다. ^^
삭제저.. 식4번에서 5번으로 넘어가는 과정에서 -cosθ(r)+sinθ(θ)가 어떻게 단위벡터 z가 되는지 알수 있을까요?
답글삭제구 좌표계의 단위 벡터 변환을 보면 됩니다. 아래 링크 참고하세요.
삭제http://ghebook.blogspot.kr/2011/07/spherical-coordinate-system.html
블로그 항상 잘보고있습니다. 혹시 dipole 말고 multipoles는 포스팅하실 계획없으신가요? 광학공부하고있는 학생인데 되게 도움많이될것같아서요. 혹은 도서추천도 좋은데 혹시 가능하신가요 ㅠㅠ
답글삭제시간될 때 다중극(multipole)에 대한 내용도 써볼게요. ^^
삭제본문에 참고문헌도 추가했습니다.
지금 jackson책으로 하고있긴한 데 이해하고있는 게 올바르게 이해한건지 판단하기가 힘들었는 데 ㅠㅠ 감사합니다!
삭제r>>d라서 R+에서 R-d/2*cos(theta)라 하셨는데 식을 어떻게 표현해봐도 d/2*cos(theta)라는 식이 나오질 않네요.. 혹시 알 수 있을까요?
답글삭제아래 링크에 있는 식 (3)과 유사합니다. 참고하세요.
삭제http://ghebook.blogspot.kr/2012/04/smallest-antenna-hertzian-dipole.html
전파거북이님이 쓰신 글들 덕분에 도움많이 받고있습니다.
답글삭제저 한가지 궁금한점이 있는데 쌍극자 모멘트 p를 그림1 에서의 벡터로 표현하면 p의 크기가 d가 될것 같은데.... 분명 쌍극자 모멘트는 Q와 d의 곱이지만 저 벡터는 Q와 관련없고 d와만 관련되어 보입니다.
제가 어디를 잘못 생각하고 있는지 알려주시면 감사하겠습니다.
전기 쌍극자 모멘트는 정의라고 생각해야 합니다. 이렇게 정의한 이유가 식 (3)에 있고요.
삭제화학1 교과서에서 쌍극자 모멘트를 표시할 때 화살표를 +에서 -로 향하게 그리던데 쌍극자 모멘트의 방향은 반대로 -에서 +가 맞는거죠?
답글삭제정말 그렇네요. 화학에서는 전기 쌍극자 모멘트를 반대로 쓰는 경우가 많네요.
삭제안녕하세요. 전자기학 공부하는 학생입니다.
답글삭제본문에 '전기 쌍극자 모멘트의 기준 방향을 전기장과 반대로 정하면 유전체(dielectric)의 성질을 표현할 때 매우 편리해진다.'
이렇게 서술되어있는데 자세히 설명해주실수 있을까요?
쌍극자모멘트는 왜 -에서 +방향으로 정의했는지 책에도 안나와서요.
[그림 4] 밑에 설명을 추가했어요.
삭제친절한 설명 감사합니다. 간단히 말해서 쌍극자 모멘트 벡터를 -에서 +방향으로 정의하면 외부전계와 같은 방향이 되므로, 쌍극자 모멘트 벡터의 부호때문에 유전체의 공식화가 간단해진다라고 이해해도 될까요?
삭제맞습니다~~
삭제전파거북이님 답변 감사합니다. 책에는 수식으로만 되있어서 이해가 어려웠는데
삭제설명듣고 많이 배우고 갑니다. 블로그로 좋은 일 하시네요. 날씨 추운데 감기 조심하세요.
식 (4)에서 전기장을 계산하면 구면 좌표계에서의 방위각 성분이 없는데 잘 이해가 안 되네요.
답글삭제수식으로는 이해가 되는데 쌍극자 전기장의 3D 그림을 보면 방위각 성분이 있는 것 아닌가요?
쌍극자의 전기장이 방위각에 관계없이 독립이라는 건 알겠는데 전기장 벡터에서 방위각 성분 자체가 없는 것이 이해가 안 됩니다.
예를 들어 r과 theta는 고정되어 있고 pi만 움직여서 관찰한다고 했을 때 pi가 30도일 때와 60도일 때는 전기장 크기가 같더라도 방향은 달라지는 것 아닌가요?
그러면 방위각 성분은 남아있어야 하는 것 같은데 제가 어디에서 착각을 하고 있는지 모르겠습니다.
도움 주시면 감사하겠습니다.
아 그리고 쌍극자 전기장 그림 주소도 첨부하겠습니다.
삭제https://www.wolfram.com/mathematica/new-in-9/built-in-symbolic-tensors/electric-potential-and-field-of-a-dipole.html
아닙니다. 방위각 방향은 반지름과 극고도각 방향과는 수직입니다.
삭제[그림 1]에 보는 것처럼 두 전하는 $z$방향으로 배치되므로, 전압의 방위각 방향 성분이 없어요. 그래서 전압의 구배인 전기장도 방위각 방향은 없습니다.
그동안 제가 구면 좌표계에 대해 겉핥기로만 알고 있었네요.
삭제구면 좌표계를 다시 제대로 공부하니까 이해했습니다.
항상 도움 많이 받고 있습니다.
감사합니다.
안녕하세요 전파거북이님 오늘도 자료 잘 조고 있어요! 게시물을 보다가 이해가 안 되는 부분이 있어서 댓글 남겨요!
삭제3번식 4번째 줄에 Qcos세타*벡터d=벡터p•r의 단위 벡터 아닌가요?
그림1을 참고하니 벡터r이 단위 벡터가 아닌 것 같아서요
문제 없네요. 참고 위해 내용을 조금 더 추가했어요.
삭제