[경고] 아래 글을 읽지 않고 "전자파의 편파"를 보면 바보로 느껴질 수 있습니다.
[그림 1] 전자기장이 가진 선형 편파[빨간색 화살표]의 진행 모습(출처: wikipedia.org)
전자기파(electromagnetic wave)가 가진 벡터적 속성을 명확히 표현하는 개념으로 편파(偏波, polarization)가 있다. 횡파(橫波, transverse wave)의 진동이 기하학적으로 기울어진 성질인 편파는 3차원 벡터인 전기장(electric field) $\bar E$나 자기장(magnetic field) $\bar H$의 방향으로 정할 수 있다. 하지만 전자파에서는 자기장 대신 전기장의 방향을 편파로 정의한다. 왜냐하면 $\bar F_e$ = $q \bar E$처럼 전기장의 방향으로 전기력 $\bar F_e$가 직관적이게 생기는 간편함이 있기 때문이다. 만약 자기장을 편파로 택하면, $\bar F_m$ = $q \bar v \times \bar B$에 따라 자속 밀도 $\bar B$와 전하 속도 $\bar v$의 벡터 외적(cross product)으로 자기력 $\bar F_m$을 계산하는 복잡함이 발생한다. 따라서 힘과 장의 방향이 같은 전기장으로 편파를 구성하는 방식이 훨씬 간단하다.
전자파의 편파는 원역장 영역(far-field region)에서 볼 때 더 명확해진다. 어떤 전자파이든지 원역장에서는 모두 평면파가 되므로[∵ 전기장과 자기장의 발산(divergence)이 0이므로 혹은 벡터 포텐셜의 진행 방향 기여가 없으므로], 전자파가 진행하는 방향 $\bar k$로는 전기장과 자기장이 없는 TEM(횡전자기, Transverse ElectroMagnetic)파 특성이 생긴다. 그래서 원역장에서 전기장은 법선 벡터(normal vector)를 $\bar k$로 갖는 평면(plane)을 만들므로, 원역장에서 독립적인 편파 성분은 항상 2개이다. 이 성분 중에서 우리가 관심 있는 혹은 사용하는 편파는 동일 편파(co-polarization), 동일 편파에 직교해 벡터 내적(dot product)이 0인 성분은 교차 편파(cross-polarization)로 이름 붙인다. 편파는 전기장으로 정의하기 때문에, 동일 및 교차 편파를 보통 $E_c$, $E_x$로 각각 표기한다. 동일 편파의 순도를 어림하기 위해 교차 편파 판별도(cross-polarization discrimination or cross-polar discrimination, XPD)도 공식화한다.
(1)교차 편파가 적을수록, 동일 편파는 커질수록 XPD는 증가한다. 정상적인 통신을 위해서는 통상적으로 20dB 혹은 25 dB 이상의 XPD가 필요하다[9]. 이런 독립적인 편파 성분에 정보를 각각 실으면, 별다른 조치가 없어도 수신부에서 통신 채널(channel) 2개를 확보할 수 있다. 이런 통신 방식을 편파 다양성(polarization diversity)이라 부른다.
근역장 영역(near-field region)에서는 편파 관계가 매우 복잡해진다. 일반적으로 $x,y,z$방향 벡터가 모두 존재하고, 원역장이나 균일 평면파(uniform plane wave)와 다르게 전기장과 자기장 관계가 $\eta \bar H$ = $\hat k \times \bar E$처럼 깔끔하게 기술되지 않는다. 여기서 $\eta$는 파동 임피던스(wave impedance)이다. 전자장 표현식(electromagnetic field representation) 관점에서 독립적인 벡터 포텐셜 $A_z, F_z$을 시작점으로 해서 모든 근역장을 만들 수 있다. 이 근역장은 6종류인 $E_x, E_y, E_z$와 $H_x, H_y, H_z$이다. 안테나의 여기 조건에 따라 전기장이나 자기장이 우세할 수 있고 6가지 벡터가 존재하므로, 근역장에서는 6가지 독립적인 벡터로 정보를 전달할 수 있다. 즉, 동일 주파수에 대해 원역장보다 근역장이 더 늘어난 전송 용량을 가진다. 다만 원역장 통신에서는 두 편파의 벡터 내적(dot product)이 0 혹은 직교하도록 맞추어 사용하지만, 근역장 통신의 경우는 6개 벡터의 벡터 내적(dot product)은 0이 아니라서 대각화(diagonalization)와 같은 추가 연산이 필수적이다.
송신과 수신 안테나를 세워서 신호를 수신하는 경우, 수신 편파를 송신 편파와 최대한 일치시켜야 최대 전력을 얻을 수 있다. 이 특성을 정량화하기 위해 전력 기준으로 편파 효율(polarization efficiency) $\eta_p$ 혹은 편파 손실 계수(polarization loss factor) PLF를 정의한다.
(2a)여기서 $0 \le \eta_p \le 1$; $\hat p_t, \hat p_r$은 각각 송신과 수신 편파를 나타내는 편파 단위 벡터(polarization unit vector)이다. 수신 안테나를 송신 안테나와 같은 방향으로 잘 세우면, 편파 효율 $\eta_p$는 최대값인 100%가 된다. 실수로 수신 안테나가 송신 안테나에 직각이 될 때는 $\eta_p$ = $0$이 되어서 송신 신호를 수신 안테나로 잡을 수 없다. 원형 편파(circular polarization)처럼 편파 단위 벡터 $\hat p$에 페이저(phasor)가 적용된 경우는 식 (1a)를 바꾸어서 페이저 기반 편파 단위 벡터 $\hat {\bf p}$를 도입한다.
(2b)여기서 $(\cdot)^*$은 각 벡터 성분에 켤레 복소수(complex conjugate)를 적용하라는 뜻이다.
광학(optics) 분야에서는 선형, 원형, 타원 등과 같이 고정된 편향을 가진 빛이라는 의미로 편파를 편광(偏光, polarized light)으로 이름 붙인다. 특정 방향으로 기울어지거나 돌아가는 편광은 편광기(polarizer)로 검출한다. 편광에 대비되는 말로 비편광(非偏光, unpolarized light)이 있다. 비편광은 편광이 무작위로 생기거나 시간에 따라 변해서 진행 방향에 따라 고정된 편향을 만들지 못한다.
1. 선형 편파(linear polarization, LP)
[그림 1.1] 선형 편파에서 전기장의 변화(출처: wikipedia.org)
편파 정의 중에서 가장 단순한 경우는 [그림 1]과 같은 선형 편파(linear polarization, LP)이다. 선형 편파는 파동이 진행할 때 전기장이 [그림 1.1]처럼 직선에 고정되어 위아래로 움직인다. 선형 편파는 보통 수직 편파(vertical polarization, VP) $\hat p_v$와 수평 편파(horizontal polarization, HP) $\hat p_h$로 나뉜다. 수직과 수평을 나누는 기준면은 지면이다. 지면에 전기장이 수직이면 수직 편파, 평행하면 수평 편파가 된다. 선형 편파를 정할 때 [그림 5.1]처럼 지면과 높이를 각각 $\hat x$와 $\hat y$로 잡아서, $\hat p_h$ = $\hat x$ 및 $\hat p_v$ = $\hat y$로 설정한 경우는 루드위그-1 정의(Ludwig-1 definition)[5]라 명한다. 수평 편파와 수직 편파가 동일한 크기와 같은 위상으로 함께 있는 편파는 경사 편파(slant polarization, SP)라 한다. 더 구분하면 지면 $\hat x$를 기준으로 45˚만큼 돌아간 편파를 경사 편파, 계속 진행해서 135˚까지 회전한 편파는 반경사 편파(anti-slant polarization)로 명한다.
(a) 아름다운 해수면
(b) 대도시의 철골 구조
[그림 1.2] 여러 가지 실제 통신 환경(출처: wikipedia.org)
실제 통신 환경에서 정보를 전송할 때는 전파 인자(propagation factor) PF가 최대값이 되게 편파를 선택한다. 예를 들어, [그림 1.2(a)]와 같은 해양 통신에서 표면은 바다이므로 수평 편파를 쓰면 바닷물의 전기 전도도(electrical conductivity)로 인해 전송 손실이 매우 커진다. 이때는 당연히 수직 편파를 기본으로 삼아야 한다. 대도시의 전파 환경은 수직이나 수평 편파가 좋다고 단정적으로 말할 수 없다. 예시적으로 [그림 1.2(b)]의 철골(steel frame) 구조를 본다. 철골이 수평으로 놓인 건물에 전파가 투과될 때는 수직 편파가 수평 편파보다 유리하다. 왜냐하면 수평 편파의 전기장이 놓인 방향으로 금속 철골이 있어서 수직 편파보다 반사가 강하게 생기기 때문이다. 하지만 모든 건물을 [그림 1.2(b)]처럼 짓지 않고 철골을 지면에 수직으로 세워서 만들기도 해서, 대도시에서는 편파에 대한 선호도가 별로 없다.
[그림 1.3] 건물 내부의 복도(출처: wikipedia.org)
[그림 1.3]처럼 건물 내부에 있는 복도(hallway)에서는 수직 편파가 수직 편파보다 전송 손실이 작다[2]. 복잡한 내부 공간에서 전자파의 편파별 손실이 다른 이유가 궁금하다. 이런 특성은 프레넬 방정식(Fresnel equation)으로 설명한다. 건물의 천장과 바닥은 철근 콘크리트(reinforced concrete)로 만들어 완전 전기 도체(perfect electric conductor, PEC)로 근사된다. 반면에 복도 옆의 벽면은 단순한 유전체로 생각할 수 있다. 그러면 벽면을 입사 평면(plane of incidence)으로 간주해 수직과 수평 편파는 각각 TE(transverse electric)파와 TM(transverse magnetic)파가 된다. 프레넬 방정식에 따르면 특정 각도에서 TM파에는 브루스터 각(Brewster's angle) 현상이 발생하므로, 반사파는 적고 투과파는 강해진다[2]. 이로 인해 복도로 전송되는 수평 편파는 벽면으로 투과하는 경우가 많아서 전송 손실이 커진다. TE파 경우는 벽면에서 반사가 여전하기 때문에 복도의 전자파는 손실을 덜 겪는다.
[그림 1.4] 편원 회전 타원체(oblate spheroid)의 예인 M&M 사탕(출처: wikipedia.org)
주파수가 밀리미터파(millimeter-wave) 이상으로 높아지면, 편파에 따른 강우 감쇠 특성이 생긴다. 빗물이 하늘에서 떨어질 때, 공기에 의한 견인력(牽引力, drag force)으로 인해 둥그런 물방울이 위아래로 찌그러져 [그림 1.4]와 같은 편원(偏圓) 회전 타원체(oblate spheroid)[모양 예시: 늙은 호박, 달걀 부침, 납작한 사탕, 호떡 등]로 바뀐다. 그러면 수평 편파는 납작한 빗물 때문에 반사가 많이 생기고[∵ 전기장 방향으로 길죽한 유전체가 존재], 수직 편파는 상대적으로 반사가 많이 생기지 않는다. 따라서 강수량이 많은 날에는 수평 편파가 수직 편파보다 손실이 커진다[3].
[그림 1.5] 구 좌표계의 단위 벡터(원본 출처: wikipedia.org)
수직과 수평 편파는 지표면에서 단거리로 통신할 때 유용한 개념이다. 하지만 항공기와 통신하거나 장거리 조건이 되면, 더 이상 사용하기 어렵다. 이때는 구 좌표계의 단위 벡터를 써서 수직과 수평 편파를 확장한다. 즉, $\hat p_v$ = $-\hat \theta$, $\hat p_h$ = $\hat \phi$로 두면 어느 위치에 있든지 수직과 수평 편파를 써서 무선 통신(wireless communication)을 분석할 수 있다.
(1.1)여기서 $\theta_i, \phi_i$는 $(\theta, \phi)$로 나타낸 입사각(incident angle)이다. 식 (1.1)을 살짝 비틀어 [그림 5.1]과 같이 하늘 방향인 높이를 $\hat z$ 대신 $\hat y$로 택할 수 있다. 이 경우는 식 (5.1)로 공식화한 $\hat p_v$ = $\hat \vartheta$, $\hat p_h$ = $-\hat \varphi$인 루드위그-2 정의(Ludwig-2 definition)[5]가 된다.
전자파에서 수직과 수평 편파가 섞인 비율은 편파각(polarization angle) $\gamma$로 표현한다.
(1.2)여기서 $\gamma$ = $0^\circ$, $90^\circ$이면 각각 수직과 수평 편파를 뜻한다.
2. 원형 편파(circular polarization, CP)
[그림 2.1] 오른손 원형 편파의 전자파 진행과 전기장 회전(출처: wikipedia.org)
전기장이 특정한 직선만을 따라 변하는 선형 편파와 다르게, [그림 2.1]에 소개한 원형 편파(circular polarization, CP)는 전자파의 진행 방향[보통 $\hat z$]을 회전축(rotation axis)으로 전기장이 회전한다. 이 전기장은 두 가지 방향인 오른손과 왼손 규칙(right- and left-hand rules)으로 돌아갈 수 있다. 더 정확하게 원형 편파는 위치를 고정하고 시간 변화에 따른 전기장의 회전 방향으로 정의한다. 예를 들어, [그림 2.1]에서 우리 위치를 원점에 두고 진행 방향을 바라볼 때, 이 전자파는 전기장이 오른손 규칙으로 돌아가는 원형 편파이다.
[그림 2.2] 오른손 규칙으로 정하는 회전 방향(출처: wikipedia.org)
[그림 2.1]을 더 쉽게 보기 위해 [그림 2.2]처럼 회전축인 진행 방향을 오른손의 엄지 손가락으로 잡고, 고정된 위치에서 시간 변화에 따른 전기장이 [그림 2.2]와 같은 원형으로 돌아가는 전자파를 상상한다. [그림 2.1]과 같은 편파는 오른손 원형 편파(right-handed circular polarization, RHCP)로 부른다. 이번에는 왼손 엄지 손가락을 진행 방향으로 삼고 왼손의 나머지 손가락 방향으로 전기장이 회전하는 경우를 생각한다. 이 편파는 왼손 원형 편파(left-handed circular polarization, LHCP)로 이름 붙인다. 오른손과 왼손이란 단어 대신 우수(右手) 원형 편파, 좌수(左手) 원형 편파로 명칭을 쓰기도 한다.
식 (1.1)과 비슷하면서도 페이저(phasor)로 각 성분별 위상을 달리해서 RHCP와 LHCP를 각각 공식화한다.
(2.1a: $e^{-i\omega t}$ 시간 약속)
(2.1b: $e^{j\omega t}$ 시간 약속)여기서 $\hat {\bf p}_l$ = $\hat {\bf p}_r^*$; 진행 방향은 $+z$축이다. 식 (2.1)이 원형 편파를 나타내는 공식을 이해하려면, 위치를 $z$ = $0$ 정도에 정하고 파동의 실수부가 시간에 따라 돌아가는 방향을 확인한다. 예를 들어, $\hat {\bf p}_r$에 대해 이 과정을 계산한다.
(2.2a: $e^{-i\omega t}$ 시간 약속)
(2.2b: $e^{j\omega t}$ 시간 약속)원형 편파의 표현식은 매우 간단하지만, 시간 약속에 따라 RHCP와 LHCP의 공식이 완전히 정반대란 사실은 큰 혼동을 유발한다. 안테나 설계에서 대형 사고를 치지 않으려면, 원형 편파의 시간 약속을 사전에 미리 선택하고 철저히 고정해야 한다.
[그림 2.3] 송신 안테나가 복사하는 RHCP를 수신 안테나가 정상적으로 수신하는 설정
원형 편파를 사용하는 송수신 안테나가 편파 손실 없이 온전한 전력을 수신하려면, 송신과 수신 모두 같은 편파를 써야 한다. 예시로써 [그림 2.3]처럼 RHCP를 복사하는 안테나의 전자파는 RHCP로 설계한 수신 안테나로 잡는다. 식 (2.1)만 단순하게 보면, RHCP와 LHCP는 $\hat y$ 관점에서 반대 위상을 가져서 RHCP를 LHCP로 수신해야 할 것 같다. 하지만 이렇게 하면 큰일난다. 왜냐하면 송신과 수신 안테나는 [그림 2.3]과 같이 서로 바로 보는 상태라서 송수신의 좌표축 정의가 다르다. [그림 2.3]에서 $y$축은 $y'$축과 정반대이다. 그래서 $e^{j \omega t}$를 쓰는 수신 기준으로 $y'$축과 연결된 안테나에서 수신된 전기장은 $E_y'$ = $-E_y (-j)$ = $j E_y$이다. 즉, 반대가 된 $y$축으로 인해 $-j$인 위상이 $+j$인 위상으로 바뀐다. 이 관계를 명확히 하기 위해 식 (2b)에서는 수신기의 편파 단위 벡터 $\hat {\bf p}_r$에 켤레 복소수를 취한 $\hat {\bf p}_r^*$를 사용한다. 푸리에 변환의 성질에 따라 주파수 영역에서 적용하는 켤레 연산[= $F^*(\omega)$]은 시간 영역에서 실수 신호(real signal) $f(t)$의 시간을 역전시킨 방식[= $\mathfrak{F}[f(-t)]$]과 동일하다. 그래서 식 (2b)는 수신기의 수신 전력을 최대로 만들 수 있는 방법을 암시하고 있다. 즉, 수신되는 신호를 예측해 시간을 역전시키거나 주파수 영역에서 켤레 복수수로 만들면, 송신과 수신의 내적을 극대화시킬 수 있다.[$\hat {\bf p}_t \cdot \hat {\bf p}_r^*$ = $\hat {\bf p}_t \cdot \hat {\bf p}_t^*$ = $1$] 이 개념은 레이다(radar)에 많이 사용되는 정합 필터(matched filter)의 출발점이다.
[그림 2.4] 원형 편파가 장애물에서 반사되어 교차 편파로 바뀌는 현상
원형 편파는 특이하게 장애물에서 반사되면, 자기 편파와 정반대인 교차 편파로 바뀌는 현상이 생긴다. 예를 들어, [그림 2.4]처럼 RHCP가 산란체에 입사할 때, 반사 현상은 기존 편파를 LHCP로 바꾼다. 왜냐하면 반사를 하더라도 전기장은 오른손 규칙으로 동일하게 돌아가지만 전자파가 전파되는 방향은 반대가 되기 때문이다. 그러면 RHCP는 LHCP로, LHCP는 RHCP로 편파가 변한다. 이로 인해 원형 편파는 반드시 산란체가 없는 환경에서 사용해야 한다. 혹은 다른 관점에서 원형 편파는 한 번 반사된 신호를 제거하기 쉽다. [그림 2.4]와 같이 RHCP를 입사시켜서 LHCP로 반사되는 경우를 본다. RHCP를 받는 수신기는 LHCP에는 편파 효율 $\eta_p$가 0%가 되므로 LHCP인 반사파가 완전히 없어진다.
[그림 2.5] 방송 위성 서비스의 예시(출처: wikipedia.org)
[그림 2.5]는 전형적인 방송 위성 서비스(broadcasting-satellite service, BSS)가 구축된 구조를 예시적으로 보여준다. 대기중에는 장애물이나 산란체가 없기 때문에 원형 편파를 쓰기 매우 좋다. 선형 편파를 써도 된다고 생각할지 모르지만 오산이다. 지구국(earth station)과 위성(satellite)은 매우 멀리 떨어져 있어서, 선형 편파를 쓰는 송수신 안테나의 방향을 제대로 맞추기가 아주 난해하다. 이때는 당연히 원형 편파를 써야 한다. 원형 편파는 안테나가 설치된 각도가 아닌 전기장이 돌아가는 방향으로 동일과 교차 편파를 구별한다. 그래서 지구국과 위성이 가시선(line-of-sight, LoS) 조건만 만족하면, 편파 효율을 100%로 가지면서 통신할 수 있다. 다만 위성 방송 수신기는 원형 편파 대신 선형 편파를 쓰기도 한다. 이는 위성이 원형 편파를 쏘더라도 선형 편파로 잡을 수 있기 때문이다. 대신 원형 편파 수신기에 비해 선형 편파 수신기는 3dB만큼 손해가 생긴다. 예를 들어, RHCP의 신호를 수직 편파로 잡을 때의 편파 효율은 50%로 줄어든다.
(2.3: $e^{-i\omega t}$ 시간 약속)RHCP 수신기로 받아도 되는 신호를 굳이 선형 편파 수신기로 받는 이유는 편의성과 가격 때문이다. 서비스 제공자(service provider) 입장에서는 어떤 수신기든지 자기 방송을 보면 유리하기 때문에, 통신 링크 혹은 접속(communication link)을 설계할 때 선형 편파로도 수신이 되게 한다. 또한 선형 편파 수신기는 [그림 2.3]과 같은 $x, y$축 위상을 조정할 필요가 없어서 가격도 저렴하다.
3. 타원 편파(elliptical polarization, EP)
[그림 3.1] 타원 편파에서 전기장이 회전하는 모양(출처: wikipedia.org)
선형 편파와 원형 편파를 모두 포함하도록 일반화한 편파는 타원 편파(elliptical polarization, EP)로 이름 붙인다. [그림 3.1]에서 보듯이 타원 편파에서 전기장 끝이 회전하는 궤적은 타원(ellipse)이 된다. 식 (2.1)과 비슷하게 $z$축으로 진행하는 타원 편파를 $x,y$ 성분으로 나타낸다.
(3.1a: $e^{-i\omega t}$ 시간 약속)
(3.1b: $e^{j\omega t}$ 시간 약속)식 (3.1)에 시간 약속을 곱하고 실수부를 선택해서 시간에 따라 회전하는 방정식을 생성한다.
(3.2a: $e^{-i\omega t}$ 시간 약속)
(3.2b: $e^{j\omega t}$ 시간 약속)조건 $E_{0x}$ = $E_{0y}$를 기준으로 $\Delta \phi$ = $-90^\circ$이면 RHCP, $\Delta \phi$ = $+90^\circ$라면 LHCP가 된다. 식 (1.2)와 (2.1)을 참고해서 타원 편파의 일반화된 편파 단위 벡터 $\hat {\bf p}_e$를 정의한다.
(3.3a: $e^{-i\omega t}$ 시간 약속)
(3.3b: $e^{j\omega t}$ 시간 약속)여기서 $E_{0x}$ = $E_0 \cos \gamma$, $E_{0y}$ = $E_0 \sin \gamma$, $E_0$ = $\sqrt{E_{0x}^2 + E_{0y}^2}$이다. 타원 편파의 궤적을 확인하기 위해 식 (3.2)에서 시간 변화를 없애서 $e_x, e_y$에 대한 식으로 바꾼다.
(3.4a)식 (3.4a)의 마지막식은 2차 곡선이므로, 판별식(discriminant)에 계수를 넣어서 $D$ = $1\cdot 1 - \cos^2 \Delta \phi$ = $\sin^2 \Delta \phi$를 계산한다. 위상차 $\Delta \phi$ $\ne$ $0^\circ$, $180^\circ$인 편파는 항상 판별식이 $D > 0$이 되어 $(e_x, e_y)$가 만드는 도형은 타원이다. 2차 곡선의 계수 행렬 $\bf A$를 고유 분해(eigendecomposition)함으로써 식 (3.4a)를 타원의 방정식(equation of ellipse)으로 변환한다.
(3.4b)여기서 $c$ = $\cos \Delta \phi$, $s$ = $\sin \Delta \phi$이다.
[그림 3.2] 회전한 타원을 위한 좌표계(원본 출처: wikipedia.org)
위상 성분 $e_x, e_y$가 아닌 [그림 3.2]에 표시한 전기장 성분 $E_x, E_y$에 대한 타원 궤적도 얻을 수 있다.
(3.5a)여기서 $\alpha$ = $\cos \gamma$, $\beta$ = $\sin \gamma$, $\beta / \alpha$ = $\tan \gamma$ = $E_{0y}/E_{0x}$; 판별식은 $D$ = $\alpha^2 \beta^2 - (\alpha \beta c)^2$ = $(\alpha \beta s)^2$이므로 2차 곡선은 타원이다. 식 (3.5)를 바탕으로 계수 행렬을 정의하고 식 (3.4b)처럼 고유 분해한다.
(3.6b)여기서 기운각(tilt angle) $\psi$를 $\tau$로 쓰기도 한다. 고유치 $\lambda_\pm$을 써서 식 (3.5a)를 타원의 표준 방정식(standard equation of ellipse)으로 간략화한다.
(3.6c)[그림 3.2]에 보인 편파가 회전하는 표준 타원(standard ellipse)의 반장축 $\overline{OA}$와 반단축 $\overline{OB}$의 길이를 결정하고 축비(axial ratio) AR 혹은 타원율(ellipticity) $\varepsilon$의 공식을 만든다.
(3.7a)
(3.7b)여기서 [그림 3.2]에 소개한 종횡비(aspect ratio) 각도 $\chi$는 축비와 연계된 매개변수이다. 축비 정의에서 조심할 부분은 위상차 $\Delta \phi$이다. 단순히 $E_{0x}$ = $E_{0y}$이면 원형 편파가 아닌 경사 편파가 나오기 때문에 축비는 무한대가 나온다. 그래서 $E_{0x}$ = $E_{0y}$ 요소와 함께 $\Delta \phi$ = $\pm \pi /2$인 조건이 반드시 필요하다.
식 (3.7b)의 마지막식에 나온 $\tan \chi$는 계산이 복잡이므로, 제곱이 나오는 $\tan (2\chi)$를 대신 사용한다.
(3.7c)
(3.7d)식 (3.7b)와 (3.7c)에 출현한 축비는 타원 편파의 중요한 특성이지만, 현업에서는 원형 편파의 존재성을 판별하기 위해 많이 사용한다. 축비는 정의상 $\text{AR} \ge 1$을 만족한다. 축비가 1이면 원형 편파, 1보다 크면 타원 편파이고 축비가 커질수록 선형 편파에 근접한다. 식 (3.7a)에 나온 복잡한 삼각 함수의 제곱은 더욱 단순한 편파 단위 벡터 $\hat {\bf p}_e$의 크기로 변경될 수 있다.
(3.8a)여기서 $1$ = $(\alpha^2 + \beta^2)^2$ = $\alpha^4 + \beta^4 + 2 \alpha^2 \beta^2$; $\bar{\bar{I}}$ = $\hat x \hat x + \hat y \hat y$는 단위 다이애드(unit dyad)이다. 식 (3.8a)를 활용해서 식 (3.7b)의 축비 정의를 단순화한다.
(3.8b: 편파 단위 벡터 $\hat {\bf p}_e$)
(3.8c: 편파 벡터 $\bar {\bf p}_e$)데시벨(decibel)로 축비를 정의할 때는 전기장 기준임을 감안해 다음처럼 계산한다.
(3.9)현실에서는 완벽한 원형 편파가 드물어서, $\text{AR} \le$ 3 dB 이내에 드는 타원 편파를 근사적인 원형 편파로 간주한다. 실제 안테나 설계에서 넓은 대역에 대해 $\text{AR} \le$ 3 dB 규격을 맞추기는 매우 어렵다.
4. 스토크스 변수(Stokes parameter)
(a) 편광 및 비편광에 대한 $S_0, S_1, S_2, S_3$ 정의
(b) 편광에 대한 $I,Q,U,V$ 정의
[그림 4.1] 스토크스 변수의 가시화(원본 출처: wikipedia.org)
타원 편파를 더욱 일반화해서 이 세상에 존재하는 모든 편파를 표현할 수 있는 근원적인 지표로 스토크스 변수(Stokes parameter), $S_0, S_1, S_2, S_3$를 정의한다[7], [10].
(4.1a)여기서 $I_t$는 광원의 전체 조도(total irradiance), $p$는 편광도(偏波度, degree of polarization), $\psi$와 $\chi$는 각각 [그림 3.2]에 나온 기운각(tilt angle)과 종횡비(aspect ratio) 각도; $I_t p$는 전체 조도 중에서 비편광을 없애고 편광만 선택한 조도이며 [그림 4.1(b)]에서 $I$에 해당한다. 대충 빛의 세기로 이해하는 $I_t$의 정확한 이름은 복사 조도(輻射照度, irradiance)이며 단위는 W/㎡이다. 복사 조도는 복사 전력(radiant power)인 복사 선속(輻射線束, radiant flux)에 수신면의 영향까지 고려한 복사 측정량이다. 편광도 $p$의 정확한 정의는 아래와 같다.
(4.1b)여기서 $I_t$ = $E_p + E_u$; $E_p$[= $I$]와 $E_u$는 각각 편광과 비편광의 복사 조도이다. 비편광이 없는 빛은 $E_u$ = $0$으로 인해 판광도가 $p$ = $1$이라서 말 그대로 완벽한 편광이다.
변수 $S_0$을 제외한 $S_1, S_2, S_3$는 [그림 4.1(a)]와 같은 구 좌표계(spherical coordinate system)를 구성한다. 예를 들어, $S_1$ = $x$, $S_2$ = $y$, $S_3$ = $z$로 두면, 스토크스 변수를 $I_t p$ = $r$, $2 \chi$ = $\pi/2 - \theta$[고도각(elevation angle)], $2 \psi$ = $\phi$[방위각(azimuth)]인 구 좌표계로 등가시킬 수 있다. 이런 방식으로 변수 $S_1, S_2, S_3$을 가시적으로 표시하는 구 좌표계 혹은 그 방식을 푸엥카레 구(Poincaré sphere)라고 이름 붙인다[10]. 푸엥카레 구는 1892년푸엥카레 38세, 조선 고종 시절에 푸엥카레Henri Poincaré(1854–1912)[개정 표기로는 푸앵카레; 개정 외래어 표기법에서 ɛ̃을 엥에서 앵으로 바꿈, 반면 ɛ은 에로 유지]가 편파 상태의 직관적 표현법으로써 제시했다. 변수 $I_t p, \chi, \psi$는 다시 $S_1, S_2, S_3$의 조합으로 표현될 수 있다.
(4.2)스토크스 변수는 영국의 대(大)물리학자 스토크스George Stokes(1819–1903)가 1852년스토크스 33세, 조선 철종 시절에 제안했다. 이때는 맥스웰 방정식이 없던 시절이라서 스토크스는 측정이 가능한 양으로 편광을 명확히 정의하려 했다[4]. 그래서 스토크스는 [그림 4.1(b)]에 소개한 $I,Q,U,V$로 편광 특성을 정했다. 변수 $I,Q,U,V$는 편광에만 적용되고 비편광을 포함하지 않는다. 요즘은 모든 종류의 빛에 대한 특성을 분석하기 위해, 편광용 $I,Q,U,V$를 확장해 타원 편파인 식 (3.2)로 만드는 $S_0, S_1, S_2, S_3$을 주로 사용한다.
[그림 4.2] 금속 모눈선(metallic wiregrid)으로 만든 선형 편광기(출처: wikipedia.org)
대략 빛의 세기인 복사 조도 $S_0$은 특정 표면에 입사하는 편광 및 비편광의 전력 밀도로 잰다. 하지만 $I,Q,U,V$ 정의는 편광에만 적용되므로, $I$ = $I_t p$는 편광만의 복사 조도이다. 그래서 $I,Q,U,V$ 정의는 $p$ = $1$인 $S_0, S_1, S_2, S_3$ 정의의 특별한 경우이다. 변수 $Q, U$는 [그림 4.2]에 보인 선형 편광기(linear polarizer)를 이용해 측정한다. 예시로 든 [그림 4.2]에서 선형 편광기는 가로로 배치한 금속 모눈선(metallic wiregrid)으로 제작된다. 이 선형 편광기를 [그림 4.2]처럼 돌리고 비편광을 가진 빛을 쏜다. 그러면 가로 방향 전기장은 반사되어 이 선형 편광기를 통과하지 못한다. 대신 세로 방향 전기장은 잘 투과되므로, 이 선형 편광기는 비편광을 수직 편광으로 바꾼다. 각도 $\phi$방향 편광을 통과시키는 선형 편광기가 출력하는 복사 조도는 $L_\phi$로 표기한다. 예시로써 [그림 4.2]에 나온 선형 편광기의 특성은 $L_{90^\circ}$이다. 따라서 $L_\phi$를 이용해 $Q, U$를 정의한다.
(4.3a)
(4.3b)여기서 $I$ = $C_r + C_l$[∵ $\hat {\bf p}_r$과 $\hat {\bf p}_l$은 정규 직교 기저(orthonormal basis)라서 길이를 보존]; $C_r$과 $C_l$은 각각 RHCP와 LHCP를 완전히 통과시키는 원형 편광기의 성질을 뜻한다. 이 개념을 더 이해하기 위해, 편광에 따른 $Q, U, V$의 변화를 [그림 4.3]에 나온 편광 그림과 변수 부호로 살펴본다. 예를 들어, 스토크스 변수가 $Q$ = $U$ = $0$이면서 $V > 0$이면 이 편파는 RHCP, 반대로 $V < 0$인 때는 LHCP를 표현한다.
(a) LP, SP, CP에 대한 Q, U, V의 대응
(b) Q, U, V의 부호의 편광 선택성
[그림 4.3] 진행 방향이 $z$축이며 빨간색으로 바뀌는 편광에 대한 $Q, U, V$의 변화값(출처: wikipedia.org)
타원 편파의 전기장 표현인 식 (3.1a)를 이용해 $I,Q,U,V$를 전기장으로 나타낸다.
(4.4a)여기서 $\bar{\bf E}$ = $E_{0x}\hat x + E_{0y}e^{-i \Delta \phi}\hat y$, $\tan \gamma$ = $E_{0y}/E_{0x}$이다. 식 (3.1b)를 써도 식 (4.4a)와 같은 결과가 얻어진다. 따라서 $I,Q,U,V$는 시간 약속과 무관하게 동일한 값을 가진다. 식 (4.4a)를 활용해 $I,Q,U,V$가 서로 만족해야 하는 관계를 유도한다.
(4.4b)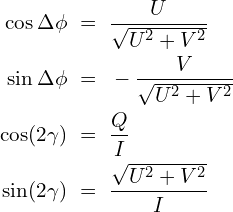
(4.4c)
(4.4d)변수 $I,Q,U,V$를 측정하는 경우, 타원 편파의 이해에 필요한 모든 변수 $\Delta \phi, \gamma, \psi, \chi$를 계산할 수 있다. 대표적으로 축비 $\text{AR}$은 식 (4.4c)를 식 (3.7)에 넣어서 만들 수 있다.
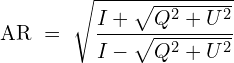(4.5)불편하게 $V$ 변수 정의에 ($-$)를 사용한 이유는 시간 약속에 관계없이 RHCP는 $V > 0$이 나오도록 만드는 목적 때문이다. 즉, 오른손 법칙처럼 RHCP에 선호하는 부호인 ($+$)를 배정한다. 반대로 식 (4.4a)의 정의로 인해 LHCP의 $V$는 항상 0보다 작게 나와서 LHCP의 $V$ 부호는 항상 ($-$)이다.
부수적으로 식 (4.1)에 도입한 $p$도 $Q, U, V$의 측정값으로 결정된다. 광원에 섞인 비편광은 무작위로 생기므로, 비편광에 대한 동일과 교차 편광의 측정값인 $E_{u,\text{co}}$, $E_{u,\text{cx}}$는 모두 존재하며 두 값은 $E_{u,\text{co}}$ = $E_{u,\text{cx}}$로 같다. 그래서 $L_\phi, C_r, C_l$에는 항상 비편광이 포함되어 있지만, $Q, U, V$에는 뺄셈으로 인해 비편광이 모두 제거된다. 또한 식 (4.3)의 측정 결과를 빼지 않고 더하면 광원의 전체 조도 $I_t$가 나온다.
(4.6a)
(4.6b)5. 루드위그 정의(Ludwig definition)
전자파의 직교 편파(orthogonal polarization)를 정의하는 창의적인 개념으로 루드위그 정의(Ludwig definition)가 안테나 특성 분석에 종종 사용된다[5], [6]. 루드위그 정의는 자주 쓰이지 않지만 모르면 안테나 전문가일 수 없어서 꼼꼼하게 알아둔다. 제안자 루드위그Arthur Ludwig(1939–)는 반사판 안테나(reflector antenna) 설계의 사실상 표준(de facto standard)인 TICRA[티크라: 전자기 복사의 영어명인 electromagnetic radiation에서 중앙의 글자를 추려서 만든 tic ra에서 유래] 프로그램 개발에 큰 기여를 했다. 미국 제트추진연구소(Jet Propulsion Laboratory, JPL) 소속이던 루드위그는 1971년루드위그 31세, 박정희 정부 시절에 덴마크 공과대학교(Technical University of Denmark, DTU)로 안식년을 가게 되었다. 이때 루드위그가 박사 과정의 결과물로 작성한 반사판 안테나용 설계 코드를 TICRA가 알게 되었다. 이 프로그램의 성공 가능성을 예견한 TICRA는 1976년에 루드위그의 코드를 바탕으로 GRASP(그라스프: 범용 반사판 안테나 SW 패키지, General Reflector Antenna Software Package)를 만들어서 TICRA 프로그램에 포함시켰고 현재까지도 계속 개선하고 있다.
[그림 5.1] 루드위그의 3가지 편파 정의(출처: [5])
[그림 5.2] 안테나를 좌표계 $(r, \alpha, \varepsilon)$으로 이동(출처: [8])
루드위그가 제안한 총 3개의 편파 정의는 안테나 해석에 쓰이는 동일 편파(co-polarization) $\hat p_\text{co}$와 교차 편파(cross-polarization) $\hat p_\text{cx}$를 $z$축 근처에서 구분할 때 유용하다.
- 루드위그-1 정의(Ludwig-1 definition): 데카르트 좌표계를 기준으로 가로축과 세로축을 각각 $x, y$로 잡고 $\hat p_\text{co}$ = $\hat y$, $\hat p_\text{cx}$ = $\hat x$로 설정한다. 이 정의는 선형 편파에 포함되며, 데카르트 좌표계처럼 좌표를 $(x, y, z)$로 구성한다.
- 루드위그-2 정의(Ludwig-2 definition): 구 좌표계를 시작점으로 하면서 높이[원래는 $+z$축이 구 좌표계의 높이] 혹은 극축(pole axis)을 새롭게 $-y$축에 두고 구 좌표계의 $(\theta, \phi)$와 비슷한 각도 $(\vartheta, \varphi)$의 단위 벡터를 사용해 동일과 교차 편파를 $\hat p_\text{co}$ = $\hat \vartheta$, $\hat p_\text{cx}$ = $-\hat \varphi$로 정한다. 통상적인 구 좌표계를 만드는 $(X, Y, Z)$ = $(x, y, z)$ $\to$ $(r, \theta, \phi)$와 [그림 5.1]의 두번째 좌표계 $(x', y', z')$ $\to$ $(r, \vartheta, \varphi)$는 $(x', y', z')$ = $(x, z, -y)$인 관계를 가진다.[$(x', y', z')$는 [그림 5.1]에 나오지 않고 $(r, \vartheta, \varphi)$로 상상한다.] 이 좌표계의 좌표 $(r, \vartheta, \varphi)$ 대신 본능적인 $(r, \text{AZ}, \text{EL})$을 쓰기도 한다. [그림 5.2]처럼 극축(pole axis)을 $-y$축에서 $-x$축으로 대체해서 단위 벡터를 $\hat \alpha, \hat \varepsilon$로 놓고 좌표를 $(r, \alpha, \varepsilon)$으로 설정할 수도 있다.
- 루드위그-3 정의(Ludwig-3 definition): 안테나 분석에 유용하도록 구 좌표계의 단위 벡터 $\hat \theta, \hat \phi$를 조합해서 동일과 교차 편파를 $\hat p_\text{co}$ = $\sin \phi \hat \theta + \cos \phi \hat \phi$, $\hat p_\text{cx}$ = $\cos \phi \hat \theta - \sin \phi \hat \phi$로 표현한다. 이 단위 벡터 $\hat p_\text{co}$와 $\hat p_\text{cx}$는 각각 구 좌표계를 위한 수직 편파 $\hat p_v$와 수평 편파 $\hat p_h$의 일반화에 해당한다. 일반화된 수평과 수직 좌표축을 써서 좌표를 $(r, h, v)$로 정의할 수 있다.
루드위그-2 정의에 나오는 $(\vartheta, \varphi)$는 [그림 5.1]을 바탕으로 나타낸다.
(5.1a)여기서 $\vartheta$와 $-\varphi$[각도가 $z$축에서 $x$축으로 변하도록 부호 ($-$)를 추가]는 각각 극고도각(polar angle)과 방위각(azimuth)에 대응한다. 좌표계 $(x,z,-y)$를 높이가 $-y$축인 구 좌표계 $(r, \vartheta, \varphi)$로 바꾸고 식 (5.1a)를 대입해, 루드위그-2 정의를 위한 동일과 교차 편파를 구한다.
(5.1b)
(5.1c)여기서 $(r, \text{AZ}, \text{EL})$를 만드는 좌표계 $(x'', y'', z'')$는 $(x'', y'', z'')$ = $(z, x, y)$인 변환을 가진다. 평면 $z$ = $0$의 정면에서 $xy$평면을 보면, 지면 역할인 $zx$평면의 $z$ = $0$에서 오른손 규칙(right-hand rule)에 따라 회전하는 방향으로 $\text{AZ}$가 정의된다. 마찬가지로 $zx$평면에서 높이를 따라 올라가는 방향으로 $\text{EL}$이 만들어진다. $\text{AZ}$와 $\text{EL}$의 단위 벡터로 만드는 편파 단위 벡터는 식 (5.1b)와 동일하게 나온다.
(5.1d)여기서 $\cos \text{EL}$ = $\sqrt{1 - (y/r)^2}$, $\cos \text{AZ}$ = $z \mathbin{/} (r \cos \text{EL})$, $\sin \text{AZ}$ = $x \mathbin{/} (r \cos \text{EL})$이다. 구 좌표계의 높이 축을 $\hat y$에 두지 않고 $\hat x$에 두는 루드위그-2 정의도 있다. 이 둘을 구별하기 위해 $\hat y$를 쓰는 [그림 5.1]의 두번째 정의를 루드위그-2I 정의(Ludwig-2I definition)라 하고, $\hat x$를 구 좌표계의 높이 기준으로 선택하면 루드위그-2II 정의(Ludwig-2I definition)라 부른다.
기존에 잘 쓰고 있는 선형, 원형, 타원 편파가 있는데도 루드위그 정의를 써야 하는 이유는 무엇일까? 루드위그 정의를 제대로 이해하려면 구 좌표계의 한계를 봐야 한다. 안테나의 송수신 특성을 분석할 때는 구 좌표계가 매우 유용하다.[∵ 안테나를 원점에 두고 구면파 형태로 복사되는 전자파를 구의 표면 위치에서 분석하기 때문이다.] [그림 5.1]에서 안테나의 복사 방향은 보통 $z$축으로 선정하고, 편파를 구성하는 전기장은 $x,y$축에 있다고 가정한다. 하지만 구 좌표계는 $\theta$ = $0^\circ$와 $180^\circ$에서 특이점이 생긴다. 이 근방에서는 비슷한 위치에 있는 점들이 살짝만 움직여도 좌표 $(\theta, \phi)$와 단위 벡터 $\hat \theta, \hat \phi$가 급격하게 바뀐다. 이런 문제점은 강체(rigid body)의 자세를 조정할 때 피해야 하는 짐벌 잠금(gimbal lock)과 비슷하다. 루드위그는 구 좌표계의 약점을 해결하기 위해, [그림 5.1]처럼 $\theta$ = $0^\circ$ 근방에서 동일과 교차 편파가 명시적으로 표현되도록 3가지 정의를 제시했다. 특히 루드위그-3 정의는 평면 주사(planar scan)를 쓰는 근역장 안테나 측정(near-field antenna measurement)에서 요긴하게 쓰인다. 평면 주사에서 모터(motor)는 탐침(probe)을 지면 $\hat x$와 높이 $\hat y$방향으로 움직여서 근역장을 잰다. 이 결과를 푸리에 변환(Fourier transform)으로 원역장에 보내면, 주빔(main beam)이 향하는 $\theta$ = $0^\circ$ 근처에서 전자장의 $\hat \theta, \hat \phi$ 성분이 심하게 변한다. 하지만 실제 안테나의 복사 패턴(radiation pattern)은 이렇게 변하지 않는다. 이때는 루드위그-3 정의를 도입해서 $\hat \theta, \hat \phi$ 성분을 선형 결합한 동일 및 교차 편파로 해결한다.
[그림 5.3] 루드위그-3 정의의 일반화(출처: [6])
[그림 5.3]은 쓸모 있는 루드위그-3 정의를 더욱 일반적인 경우로 확대하기 위한 좌표계를 보여준다. 원래 제안된 루드위그-3 정의는 $\theta$ = $0^\circ$ 주변이 관심 지역이다. 하지만 구면 주사(spherical scan)처럼 구 좌표계의 임의각 $(\theta, \phi)$에서도 루드위그-3 정의를 사용하려면, 원래 공식의 각도 $\phi$를 [그림 5.3]에 보인 일반화 각도 $\zeta$로 바꾼 일반화 루드위그-3 정의(generalized Ludwig-3 definition)를 채택한다[6].
(5.2a)각도 $\zeta$를 구하려고 피시험 안테나(antenna under test, AUT)의 전기장은 개구 평면(aperture plane)인 $xy$평면에 있다고 가정한다. 이 개구 전기장이 공간 상으로 퍼진 전기장 $\bar E_s$ = $E_s \hat p_\text{co}$는 임의 방향으로 성분을 가진다. 단순화를 위해 전기장 $\bar E_s$에서 개구면인 $xy$평면에 평행한 요소 $\bar E_t$를 추출한다.
(5.2b)여기서 $\hat \theta$ = $\cos \theta \hat \rho - \sin \theta \hat z$이다. 접선 전기장 $\bar E_t$를 구성하는 성분이 형성하는 편파각(polarization angle)은 [그림 5.3]에 표시한 $\xi$이다.[편파각 $\zeta$는 식 (1.2)과 (3.3a)에 쓴 $\gamma$에 해당한다.]
(5.2c)여기서 $\xi$는 $E_\phi$에서 시작해 $E_\rho$ 방향으로 잰 각도이다. 편파각 $\xi$의 기준점을 $\hat x$로 바꾼 새 편파각을 [그림 5.3]처럼 $\phi'$라 한다. 그러면 $\phi'$ = $\phi + (\pi/2 - \xi)$이다. 이 결과를 식 (5.2c)에 대입해서 $\zeta$를 유도한다.
(5.2d)여기서 $(\theta, \phi)$는 일반화 루드위그-3 정의를 적용할 구면상의 위치, $\phi'$는 $\hat x$축에서부터 개구면을 따라 잰 편파각이다. 통상적으로 편파각은 $\phi'$ = $90^\circ$로 설정한다. 물론 편파각을 $90^\circ$ 대신 $0^\circ$로 선택해도 전혀 문제없다. 다만 다이폴 안테나(dipole antenna)와 같은 기본 안테나를 지면에 대한 수직 편파로 설정해서 측정하는 경우가 많아서 $\phi'$ = $90^\circ$를 많이 쓴다는 뜻이다. 그러면 식 (5.2d)를 $\tan \zeta$ = $\tan \phi \mathbin{/} \cos \theta$로 단순화할 수 있다. 여기에 $\theta$ = $0^\circ$를 넣으면 $\zeta$ = $\phi$가 되므로, $\phi'$ = $90^\circ$와 $\theta$ = $0^\circ$에서 일반화 루드위그-3 정의는 기존 루드위그-3 정의에 부합한다.
[참고문헌]
[1] I. Naito, "A note on representation of electromagnetic plane wave polarization state," IEEE Trans. Antennas Propag., vol. 70, no. 7, pp. 6066–6071, Jul. 2022.
[2] P. Kyritsi and D. C. Cox, "Propagation characteristics of horizontally and vertically polarized electric fields in an indoor environment: Simple model and results," IEEE Veh. Technol. Soc. Conf. Proc., vol. 3, pp. pp. 1422–1426, Oct. 2001, Atlantic City, NJ, USA.
[3] Specific Attenuation Model for Rain for Use in Prediction Methods, Recommendation ITU-R P.838-3, Mar. 2005.
[4] J. Tatum, 4.1: Polarized Light and the Stokes Parameters, Physical Optics, The LibreTexts, CA, USA.
[5] A. Ludwig, “The definition of cross polarization,” IEEE Trans. Antennas Propag., vol. 21, no. 1, pp. 116–119, Jan. 1973.
[6] J. E. Roy and L. Shafai, "Generalization of the Ludwig-3 definition for linear copolarization and cross polarization," IEEE Trans. Antennas Propag., vol. 49, no. 6, pp. 1006–1010, Jun. 2001.
[7] J. J. Condon and S. M. Ransom, Radiation Fundamentals, Essential Radio Astronomy, National Radio Astronomy Observatory, VA, USA, 2015. (방문일 2022-03-29)
[8] A. C. Newell and G. Hindman, "Antenna spherical coordinate systems and their application in combining results from different antenna orientations," ESA ESTEC Workshop on Antenna Measurements, 1999. (방문일 2024-01-28)
[9] Fixed Radio Systems; Characteristics and Requirements for Point-to-point Equipment and Antennas; Part 4: Antennas, Draft ETSI EN 302 217-4, V2.2.0, Apr. 2025.
[10] Z. Sun, "Poincaré sphere and Stokes parameters of orbital angular momentum wave based on Euler’s formula," Opt. Lett., vol. 50, no. 13, pp. 4382–4385, Jun. 2025.
[다음 읽을거리]
글이 안보이는데 수정중이신건가요?
답글삭제네 ^^ 재미있는 내용이라서 꼼꼼히 쓰고 있어요.
삭제ㅎㅎㅎ 기대하고 있겠습니다.
삭제