1. 뉴턴의 운동 법칙
2. 에너지의 개념
3. 균일 평면파의 의미
4. 포인팅의 정리
[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.
 (1)
(1)
식 (1)에서 전자파의 속도는 $c$로 일정하기 때문에 전자파가 전달되는 속도 방향 운동량 $p_c$는 다음으로 쓸 수 있다.
 (2)
(2)
여기서 $v$는 우리가 적분하려는 체적(volume)이다. 식 (2)의 좌변에 있는 운동량도 우변의 전자파 에너지 밀도(energy density of electromagnetic wave)처럼 단위 체적당 운동량 $\mathfrak{p}_c$로 바꾸면 다음을 얻는다.
 (3)
(3)
식 (3)을 간략화하기 위해 우리가 생각하는 전자파를 균일 평면파(uniform plane wave)로만 한정하자. 먼저 평면파의 다음 성질을 기억하자.
 (4)
(4)여기서 $\bar k$는 파수 벡터(wavenumber vector)이다. 식 (4)를 식 (3)에 대입하면 다음을 얻는다.
 (5)
(5)여기서 $\bar k$ = $k_0 \hat k$, $k_0$ = $\omega \sqrt{\mu_0 \epsilon_0}$, $\eta_0$ = $\sqrt{\mu_0 / \epsilon_0}$이다. 전자파 운동량의 방향은 파수 벡터의 방향이어야 하므로 식 (5)를 벡터적으로 표현하면 다음과 같다.
신기하게도 전자파 운동량 밀도(momentum density)는 포인팅 벡터(Poynting vector)와 밀접한 관계를 가진다. 또한 전자파의 복사 압력(electromagnetic radiation pressure) 정의 $\mathfrak{\bar f}$를 이용하면 다음 관계도 얻는다.
 (7)
(7) (8)
(8)위 정의에서 켤레 복소수(complex conjugate)는 큰 의미없다. 켤레 복소수가 들어간 정의는 페이저(phasor)를 사용한다는 뜻이다. 식 (8)의 전자파 운동량 밀도를 이용해 전자파의 각운동량 밀도(angular momentum density)를 정할 수 있다.
 (9)
(9)
아래 맥스웰 방정식을 식 (9)에 대입하면 다음을 얻는다.
 (10: 패러데이의 법칙)
(10: 패러데이의 법칙) (11)
(11)식 (11)에 다음 벡터 항등식(vector identity)을 적용해보자.
 (A.1)
(A.1) (A.2)
(A.2) (12)
(12) (13)
(13) (14)
(14)
또한 우리가 계산하고 있는 양은 각운동량 밀도이므로 식 (14)는 다음 체적 적분과 관련되어 있다.
 (15)
(15)
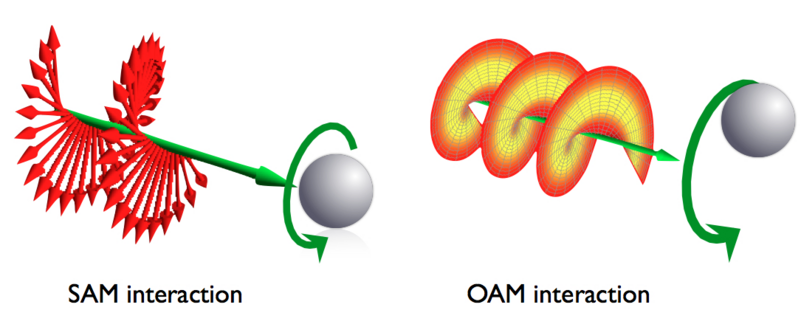
[그림 1] 자전과 공전 각운동량(출처: wikipedia.org)
식 (15)를 식 (12)에 대입하면 전자파의 각운동량 밀도를 다음 두 성분으로 나눌 수 있다.
 (16)
(16)
$\mathfrak{\bar J}_{\rm SAM}$은 선형 편파(Linear Polarization, LP) 경우 0이고 원형 편파(Circular Polarization, CP)는 값이 있으므로 자전 각운동량(Spin Angular Momentum, SAM)이라 부른다. 자전 각운동량은 원형 편파이므로 전자파 전달축 중심에서도 전기장과 자기장이 존재한다.[물론 원형 편파이므로 파면 전체에서 전자파 전력의 분포는 동일하다.] $\mathfrak{\bar J}_{\rm OAM}$은 축[$\bar r$]을 기준으로 계산하고 있으므로 공전 각운동량(Orbital Angular Momentum, OAM)이라 한다. 자전 각운동량과는 다르게 전자파 전달축 근방에서는 전자파 전력이 없고, 전달축에서 떨어진 특정한 반지름 위치의 전자파 전력이 최대가 된다.[전자파의 전력 분포 특성이 공전 궤도와 매우 유사하다.]

[그림 2] 정지한 하전 입자에 입사하는 균일 평면파
전자파의 운동량을 더 정확히 이해하기 위해 [그림 2]처럼 정지한 하전 입자에 작용하는 전자파 특성을 살펴보자. 초기 조건[$t$ = $0$]에서 정지[$v_x$ = $v_z$ = $0$]해 있는 하전 입자에 균일 평면파(uniform plane wave)가 입사하면 전기장에 의해 하전 입자가 가속된다. $x$방향으로 가속된 하전 입자는 자기장에 의해서도 영향을 받는다. 매우 작은 시간인 $t$ = $\Delta t$에서 변화된 $x$방향 속도와 자기력은 다음과 같다.
 (17)
(17)식 (17)을 이용해 운동 에너지와 $z$방향 운동량을 계산한다.
 (18)
(18)식 (18)에 제시한 결과는 식 (2)와 정확히 일치한다. 재미있는 결과지만 의문이 생긴다. 분명 전기장에 의해 $x$방향으로 가속이 되는데, 운동량 증가는 $z$방향으로 생긴다. 어떻게 해서 이런 현상이 생길까? 단순하게 보면 전자파는 식 (6)과 같은 운동량을 가지기 때문에, 전자파가 가진 운동량이 하전 입자에 전달되어 $z$방향 운동량이 생긴다고 설명할 수 있다. 이런 정성적인 설명을 바탕으로 로렌츠 힘(Lorentz force)을 이용해 좀더 정량적인 분석을 해보자.
 (19)
(19)식 (19)에 등장한 미분 방정식을 풀면 $x, z$방향 속도를 다음처럼 구할 수 있다.
 (20)
(20)사이클로트론(cyclotron) 동작 원리와 유사하게 $v_x$는 $+x, -x$방향을 진동하고 있다. 따라서 $x$방향 평균 운동량은 0이 되어, 전체 운동량에 기여하는 성분은 없다. 하지만 $z$방향 속도는 상수항이 있으므로, $z$방향 평균 운동량[$\langle p_z \rangle$]은 $mc$로 일정하다. 전기력과 평균 운동량과의 관계는 다음과 같다.
 (21)
(21)또한 식 (20)에서 $t \approx \Delta t$로 근사하면 식 (17)과 (18)을 얻을 수 있다.
이상의 논의에서 전자파 운동량은 식 (6)처럼 하전 입자에 직접 작용함을 볼 수 있다. 전자파에 전기장은 항상 있지만, 전기장이 하전 입자에 전달하는 전기력은 상쇄되어 사라진다. 대신에 전자파 에너지가 전달되는 방향으로 하전 입자에 운동량이 전달된다.
[참고문헌]
[2] K. T. McDonald, "Orbital and spin angular momentum of electromagnetic fields," Physics Examples, 2009.
[3] R. N. C. Pfeifer, T. A. Nieminen, N. R. Heckenberg, and H. Rubinsztein-Dunlop, "Momentum of an electromagnetic wave in dielectric media," Rev. Mod. Phys., vol. 79, no. 4, pp. 1197–1216, Oct. 2007.
[다음 읽을거리]
1. 자기 단극자
전자파의 운동량 Pc가 왜 저렇게 (2)와 같이 나오는지는 잘 모르겠습니다. ㅠ_ㅠ
답글삭제전자파의 속도가 일정하기 때문인데요 아래 링크의 식 (11)에 증명되어 있습니다.
삭제http://ghebook.blogspot.kr/2011/09/energy.html
위 식 (2)의 가장 우변은 전자파의 에너지 밀도입니다. 아래에 증명되어 있습니다.
http://ghebook.blogspot.kr/2011/03/poyntings-theorem.html
안녕하십니까 동아대학교 신소재공학과에 다니는 학생입니다. 죄송합니다만 여쭙고 싶은것이 있는데 특허문제로 글로 남기기는 힘들것같아서 실례인줄 알지만 연락 주시면 안될까 여쭙습니다. 010 4414 1246 으로 연락 부탁 드려봅니다
답글삭제필요하면 iGhebook@Gmail.com 으로 이메일 주세요. ^^
삭제질문은 언제든 환영합니다.
확인] 본 페이지는 exp(-iωt) 시간약속을 사용하고 있습니다.
답글삭제이 도대체 무슨말인지요? 시누소이드 파형과 같이 정확하다는 의미인가요?
아닙니다. 페이저(phasor)를 정의할 때 어떤 시간 기준을 사용할 것인지를 명시한 것입니다.
삭제아래 링크 참고하세요.
http://ghebook.blogspot.kr/2010/10/maxwells-equations-using-phasor.html
15식은 왜 0이 되는 것인가요? 궁금합니다. ~~
답글삭제우리가 생각한 면적 적분의 방향을 $r$방향으로 정했습니다. 그래서, 피적분 함수와 면적 적분소가 수직이 되어 0이 됩니다.
삭제식 (5)에서, 공간에 저장된 에너지량을 포인팅 벡터를 c로 나눈 값으로 표현하셨는데 포인팅 벡터 자체가 에너지 벡터인데 그런 결론이 가능한지 잘 받아들여지지 않습니다. 제가 잘못생각하고 있는건가요?
답글삭제다시 생각해보니, 포인팅 벡터는 에너지가 아닌 전력 벡터라고 보는게 맞군요! 그럼, 전력벡터를 c로 나눈 것이 곧 에너지밀도라는 결론이 나오는 것인가요?
삭제포인팅 벡터의 속도가 c이기 때문이군요.
삭제식 (5) 위쪽에 있는 설명이 식 (5)의 증명입니다. 포인팅 벡터는 전기장과 자기장으로 구성되기 때문에 이동 속도는 항상 광속($c$)입니다.
삭제전자파 각운동량의 분해를 명쾌하게 보여 주셔서 감사합니다.
답글삭제몇가지 질문이 있습니다.
1) Momentum을 정의 할때 마지막에 체적 적분이 되어야 하는것이 아닌가요? 기준점 r에 대하여?
2) linear momentum과 angular momentum을 나눌때? 에너지 보존은 어떻게 되나요? Poynting vector를 기준으로.... 저식으로는 선형운동량의 요소가 각운동량의 요소가 될수 없어 보이는데..
3) 참고한 reference 를 알수 있을까요? (SAM+OAM)
감사합니다. 항상 정말로 잘 보고 있습니다.
방문 감사합니다, PWC님. ^^
삭제1. 유도 과정에서는 모두 (각운동량의) 밀도로 표현했습니다. 각운동량을 얻으려면 당연히 체적 적분을 하면 됩니다.
2. 유도의 출발점은 포인팅이 예측한 전자파의 운동량입니다. 이걸로 각운동량을 정의해 계산한 것입니다.
3. 전자파 각운동량이 SAM과 OAM으로 분리된다는 걸 보고 한 번 해본 것입니다. SAM과 OAM으로 검색하면 참고문헌이 많이 나오네요. [2]에 하나 더 추가했습니다.
답글 감사합니다.
삭제한가지 더 질문 드리면...
SAM, OAM이 가지는 공식에 대한 물리적 의미를 설명해주실 수 있나요?
감사합니다.
SAM과 OAM은 자전과 공전을 생각하면 됩니다.
삭제전자파에서 자전에 해당하는 것은 원형 편파(CP: circular polarization)를 의미합니다.
공전은 전자파 분포 관점에서 봐야 합니다. 축방향 중심에는 전자파 전력이 거의 없고, 특정한 반지름 위치에 전자파 전력이 최대가 됩니다.
질문 하나 더 드리겠습니다ㅜㅜ
삭제식 (4)를 식 (3)에 대입해서 식 (5)를 얻는 과정을...잘모르겠습니다.
plane wave를 가정 하고 파수벡터 k를 이용해 계산하는건 알겠는데, (4)이용,
그 과정을 따르는 벡터 표시들을 무엇이며 어떻게 유도된 것인지 설명해 주실수 있나요?
다시 말해 계산이 이해가 안갑니다....
vector_E = vector_k X vector_H / (-we) 아닌가요? 어디서 hat_k? hat_E가 나오나요?
감사합니다.
상수항을 잘 대입하면 됩니다. 본문에 내용 약간 추가했어요.
삭제감사합니다 잘 정리 되네요!!
삭제혹시 전자기파의 운동량 및 계산에 대해 질문을 할 수 있을까요?
답글삭제전자기파의 운동량도 무한대가 될수 있나요? 그리피스라는 전자기학 과목이 있는데요.
q2인 입자가 등속으로 z축 방향으로 움직이고 q1인 입자는 원점에서 정지해 있을 때
q2에 의한 자기장과 q1에 의한 전기장으로 운동량을 구하면 쉽게 구해지는데
q2에 의한 자기장과 과 전기장으로 운동량을 계산을 하면 무한대가 나옵니다.
여기서 제가 계산한 방법은 q2가 있는 곳을 기준으로 하여 구좌표계로 계산하였는데 무한대가 나와습니다.
운동량이 무한대일 경우도 있나요? 아니면 제가 계산을 틀리게 한 것인가요?
힘을 구하기위해 시간에 대해 미분해야하는데 답이 무한대가 나와서 시간에 대해 미분하면 상관이 없는지 궁금합니다. 저의 계산이 틀린다면 저의 풀이 과정을 검토해 줄 수있나요? ㅠㅠ
평면파인 경우는 전자기파의 운동량이 무한대로 나옵니다.
삭제계산할 때 점 전하 가정해서 무한대가 나온 것인가요? 어쨌건 포인팅 정리에 의해, 특정 영역의 운동량이 발산하면 해당 원천의 에너지가 무한대라는 뜻입니다.
네, 전하량 q1,q2 둘 다 점입자라고 생각하고 운동량을 계산 할떄 q2에 의한 자기장과 q1에 의한 전기장을 구하후 포인팅벡터를 구하고 원점을 중심으로 구좌표계에 대해 모든 공간 적분하면 유한값이 나오는데
삭제q2에 의한 자기장과 q2에 의한 전기장을 구한 후 포인팅벡터를 구하고 q2가 있는 점을 기준으로 모든 공간에 대해 적분하면 무한대가 나옵니다. ㅜㅜ
q2가 있는 점 vt곳을 기준으로 구좌표계로 계산했습니다. (x,y,z)-(0,0,vt)
삭제위에서도 말씀드렸듯이 점 전하의 전기장이 무한대인 영역이 있어, 운동량 밀도도 무한대이고 이걸 체적 적분한 운동량도 그 영역에서 무한대입니다.
삭제무한대 나왔다고 틀린 계산을 한 것은 아닐 겁니다. 하지만 적분 위치에 따라 무한대 아닌 경우가 있는 것은 이상하네요.
q2를 원점으로 하여 계산하면(vt=0, 0으로 간주해도 되나요?) r의 적분 범위가 0~무한대인데 여기서도 답은 무한대로 나옵니다. q2에의한 전자기장 운동량만 무한대가 나오는 상
삭제황입니다. q1(전기장) q2(자기장) 의한 전자기 운동량은 유한값이 나옵니다. 적분위치에 따라 무한대가 아니라는 말은 q1q2에 의한 전자기운동량 말하는 것인가요?
식 (6)을 이용해 전자파의 운동량을 계산한다면, 단순 체적 적분이라서 적분 영역이 같으면 원점을 어떻게 두든지 결과는 같아요.
삭제- 말씀하신 두 전하의 전자장은 서로 상호 작용하지 않기 때문에 각각 계산해 더하면 됩니다. 중첩의 원리(superposition principle)를 쓰면 되요.
- 등속 운동하는 전하는 전기장과 자기장을 동시에 만들어요. 그렇다고 전자파가 발생하는 것은 아니고요. [체렌코프 복사(Cherenkov radiation)는 예외]
헤헤..답변 고맙습니다.
삭제1 "적분 위치에 따라 무한대 아닌 경우가 있는 것은 이상하네요." 잘 이해가 가지 않습니다.
2.등속 운동하는 전하가 전자파를 발생하지 않는 다는 것은 운동량을 만들지 않는 것인가요?
1. 단순한 적분에 대한 얘기입니다. 적분은 좌표계 바꾼다고 결과값이 바뀌지 않아요.
삭제2. 식 (6)으로 표현된 운동량은 있어요. 하지만 이 운동량 밀도의 발산이 없기 때문에 전자파는 없어요.
발산이 없다는 것은 유한값이 아닌가요? 운동량 밀도가 발산이면 무존것 전자파가 존재 한다는 것인가요?
삭제포인팅 벡터의 발산과 관련해서 아래 링크 참고하세요.
삭제http://ghebook.blogspot.kr/2011/03/poyntings-theorem.html
발산이 더이버전스 말하는 것인가요???
삭제맞습니다.
삭제발산이 없다는 것이 0아 아닌 정의를 할 수 없어서 그렇것인가요?
삭제발산 연산자에 대해 더 세부적으로 보시면 아시겠지만, 발산이 0이라는 뜻은 "해당 체적에 들어온 벡터만큼 동일한 벡터가 빠져 나가서 내부에 쌓이거나 생성된 벡터가 없다"를 의미합니다.
삭제답변 고맙습니다. 알듯 말듯 하네요 헤헤..
삭제그렇면 발산이 없다는 말은 0을 포함한 유한값도 없다고 이해 해도 되나요?
제가 이해 한것을 끄적어 내면
"등속으로 움직이는 전하 입자가 순간 원점에 있다고 했을 때 포인팅벡터를 구하면 r^(-4)이 나오는데 이는 발산을 할 수 없는 식이기 때문에 전자파는 존재 하지 않는다."
이렇게 생각하는 것이 옳은 것인가요?
1. 발산이 없다는 것은 0이라는 뜻입니다.
삭제2. 등속 운동하는 전하의 포인팅 벡터 발산을 구하려면 포인팅의 정리를 적용하면 됩니다. 원천에 대한 체적 적분이 0이기 때문에 발산이 0이에요.
1. 포인팅벡터 발산이 0이면 전자기운동량밀도의 발산도 0인데
삭제이렇게 되면 운동량밀도는 운동량밀도가 발산이 0이어도 유한값이 존재 할 수 있나요?
2. 이해가 안되서 위키백과의 https://ko.wikipedia.org/wiki/%ED%8F%AC%EC%9D%B8%ED%8C%85_%EB%B2%A1%ED%84%B0
포인팅 정리 식에서 원천에 대한 체적적분은 어는 부분을 말하는 것인가요?
익명님, 답변이 충분히 된 것 같습니다. ^^ 위 댓글에도 말씀드렸듯이 발산과 포인팅 정리를 다시 한 번 보세요.
삭제1. 발산이 0이라고 벡터가 0인 것은 압니다.
2. 전류와 자류 밀도 있는 부분이 원천입니다.
위의 포인팅정리를 보니 평균 포인팅 벡터가 0이 원천에 대한 체적 적분이 0을 의미 하는 것인가요? 평균이 아닌 벡터에서는 어떻게 되는 것인가요?
삭제답변을 기다리고 있습니다. ㅠㅠ
답글삭제추가하신 내용 감사히 잘 봤습니다.
답글삭제각운동량을 예로 들면, 각운동량 역시 운동량 방향(Poynting vector)으로 운동량이 생기고, 마찬가지로 양자화(정량화)된 상수를 얻을 수 있습니다. 물리학에 photon의 개념으로 생각할수 있고 역으로 계산해서 전자기파의 각운동량을 판단하는 정량상수로 이용 할 수 있습니다.
이부분에서 물리학(광학?)과 전자기학의 개념들이 서로 맞물리며 멱살잡고 싸우기 시작하는데요.....혼란스럽습니다ㅜㅜ
안녕하세요 전파거북이님. 궁금한점이 있어 이렇게 댓글을 남깁니다.
답글삭제일반적으로 가속도 운동을 하는 전자는 힘을 받아 AC측면으로 생각해 전자파가 나온다고 생각이 되는데,
하지만 원자핵을 도는 전자는 등속 원운동하여 속도는 일정하지만 방향이 바뀌어 가속도 운동을 하게 되는데 그러면 이 경우 전자한테 전자파가 나오는지 궁금합니다.
하지만 방향은 바뀌어도 속도가 변하지 않기때문에 DC측면으로 생각해 전자파가 나오지 않는다고 생각하는데 제 생각이 맞을까요?
1. 원자핵의 전자가 원 운동하면 가속이 생기기 때문에 당연히 전자파가 나옵니다. 이걸 설명하는 과정이 양자 역학의 발전 역사입니다.
삭제2. 전자가 등속 운동(DC)해도 전자파가 나오는 경우가 있습니다. 이 부분은 체렌코프 복사를 찾아보세요.
1의 추가: 하지만 전자파가 나오면 에너지가 손실되어 결국 원자가 붕괴되기 때문에, 현실에서는 전자파가 나오지 않습니다. 따라서 전자기학이 원자 설명에 적용될 때 심각한
삭제문제가 생깁니다.
안녕하세요 전파거북이님, 애독자 중 한명입니다.
삭제위와 같은 상황은 음전하가 등속원운동하고 있는 상황이고 이는 원형도체선로에서 일정한 전류가 흐르고 있는 상황과 같이 모델링할 수 있다고 생각됩니다.
이런한 경우 원형고리 특정지점의 자계의 세기를 비오사바르 법칙을 통해 구한다면 시간에따라 변하는 것이 아닌 거리에 대한 함수값으로 나오는 것으로 알고있습니다.
전자파는 자계 또는 전계가 시간에 따라 변해야만 생성되는 것으로 알고 있는데 이에 관해 혹시 설명 해주실 수 있을까요?
그리고 만약 이러한 상황에서 전자파가 나온다면 어떤 방향으로 방사되어 진행될지 궁금합니다.
항상 친절한 답변 감사드립니다.
하전 입자의 원 운동을 전자파로 계산하기는 쉽지 않습니다. 단순하게 전류로 가정한다면, 루프 안테나(loop antenna)로 볼 수 있어 안테나 관점으로 계산하면 됩니다. (그렇다고 쉽지는 않아요. ㅠㅠ)
삭제루프 안테나의 주빔 방향은 반지름에 따라 달라집니다.