고유 함수의 완비성(Completeness of Eigenfunctions)

[경고] 아래 글을 읽지 않고 "고유 함수의 완비성"을 보면 바보로 느껴질 수 있습니다.
1. 스튀름–리우빌 이론
2. 푸리에 급수의 시작

[그림 1] 푸리에 급수의 완비성(출처: wikipedia.org)

스튀름–리우빌 이론(Sturm–Liouville theory)의 최종 목표는 푸리에 급수(Fourier series)를 이해하기이다. 푸리에 급수는 왜 수렴하며, 직교성(orthogonality)과 완비성(completeness)을 왜 가질까? 다른 함수도 이런 특성을 가지고 있는가? 1807년푸리에 39세, 조선 순조 시절에 등장한 푸리에 급수의 성공을 수학적으로 완벽하게 이해하기 위해 스튀름Jacques Charles François Sturm(1803–1855)은 1829년스튀름 26세, 조선 순조 시절부터 스튀름–리우빌 이론에 대한 다수의 논문을 발표한다. 1837년에는 리우빌과 함께 네 쪽짜리 논문을 썼다. 이 논문은 짧지만 스튀름–리우빌 이론의 정수를 보여준다[1]. 스튀름의 진동 정리(Sturm's oscillation theorem)를 쓰면 푸리에 급수가 가진 완비성을 모든 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)으로 확장할 수 있다.

[고유 함수의 완비성]

고유치(eigenvalue) $\lambda_m$에 대한 직교 정규 고유 함수(orthonormal eigenfunction)가 $\psi_m$인 경우 제곱 적분 가능한 함수(square-integrable function) $f$는 고유 함수의 무한 급수로 항상 표현 가능하다.

                   (1)

여기서 내적(inner product)과 직교 정규 고유 함수는 다음과 같이 정의한다.

                       (2: 내적)

                       (3: 직교 정규 고유 함수)

                      (4: 크로네커 델타)

[증명]

고유 함수의 완비성 증명 시작은 식 (5)의 레일리 몫(Rayleigh quotient)이다[2].

   (5)

레일리 몫에 의해 고유치는 고유 함수의 내적으로 표현할 수 있다. 처음에 레일리 몫을 보면 의미없는 공식같지만 고유 함수의 완비성을 증명하는 새로운 길을 제시한다. 식 (6)의 스튀름 진동 정리를 적용한다.

                      (6)

스튀름의 진동 정리에 의해 고유치는 최소값을 반드시 가진다. 그래서 정칙 경계 조건(regular boundary condition)을 만족하는 임의의 함수 $f$를 식 (5)의 정의에 대입해서 다음 부등식을 얻는다.

                      (7)

여기서 $f$는 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)을 만족하며 제곱 적분 가능(square integrable)해야 한다.

                      (8)

스튀름–리우빌 이론에서는 기본적으로 고유치를 선택한 상태에서 경계 조건을 만족하는 고유 함수를 고유치에 대응해서 구한다. 하지만 식 (7)의 시작점은 고유치가 아니고 우리가 고려하는 $f$이므로, 지금까지 쓰던 기본 방법론에서 약간 어긋나있다. 이후에 $f$에 대응하는 고유치 $\lambda_f$를 레일리 몫으로 찾는다. 이 $\lambda_f$는 식 (7)처럼 가장 작은 고유치 $\lambda_0$보다 크거나 같아야 한다. 왜냐하면 스튀름의 비교 정리(Sturm's comparison theorem)에 따라 정의 구간 내에서 영점 개수가 가장 작은 경우는 $\lambda_0$를 가진 $\psi_0$이고 $\lambda_f$를 품은 $f$의 변화가 $\psi_0$보다 느려질 수 없기 때문이다. 예를 들어, $f(x)$ = $\psi_i(x) + \psi_j(x)$이고 $\lambda_i < \lambda_j$인 조건에서 식 (5)로 얻는 고유치는 $\lambda_f$ = $\lambda_i + \lambda_j$가 됨으로 인해 $\lambda_i < \lambda_f$를 얻는다.[식 (5)로 계산할 필요없이 각 고유 함수에 대한 스튀름–리우빌 미분 방정식을 더한 후에 $\psi_i(x) + \psi_j(x)$로 내적을 적용해서 $\lambda_f$를 더 쉽게 정할 수 있다.] 결국 레일리 몫은 $f$의 고유치를 생성하는 연산이므로, 스튀름–리우빌 미분 방정식이 성립하는 $f$가 얻을 수 있는 고유치는 $\lambda_0$보다 작아질 수 없다. 다음 단계로 함수 $f$와 관계되지만 고유 함수 $\psi_0$의 영향은 없는 함수를 $g_0$이라 한다. 이를 통해 $g_0$의 단순한 표현식을 도출한다.

                      (9)

마찬가지로 함수 $g_0$와 관계되지만 고유 함수 $\psi_1$의 영향이 없는 함수는 식 (9)와 유사하게 $g_1$로 정의할 수 있다. 이 과정을 계속 반복해서 $\psi_0, \psi_1, \cdots, \psi_M$의 영향이 없는 함수 $g_M$을 다음처럼 규정한.

                      (10)

여기서 $m$ = $0, 1, 2, \cdots, M$이다. 또 하나 생각할 부분은 $g_M$이 $\psi_0, \psi_1, \cdots, \psi_M$의 영향이 없기 때문에 식 (5)와 (7)에 의해 다음 부등식이 성립하게 된다.

                      (11)

여기서 $g_M$은 $\lambda_0, \lambda_1, \cdots, \lambda_M$과 관계가 없어서 $g_M$의 레일리 몫은 $\lambda_{M+1}$보다 항상 크거나 같아야 한다. 또한 식 (11)의 우변에 있는 내적의 의미를 파악한다.

                      (12)

                      (13)

여기서 $M_0$는 고유치 $\lambda_m$이 ($-$)인 최대 정수이다. 즉, $m \le M_0$이면 $\lambda_m \le 0$이다.

식 (12)와 (13)을 식 (11)에 대입하고 정리하면 다음과 같다[2].

              (14)

식 (6)의 스튀름 진동 정리에 의해 고유치는 무한대로 커져서 $M$이 무한대로 커질 때에 식 (14)의 우변은 0으로 수렴한다. 그래서 $E_M$이 0으로 수렴하므로 고유 함수의 완비성인 식 (1)이 항상 성립한다.

______________________________

이로써 푸리에 급수를 포함한 스튀름–리우빌 이론의 고유 함수는 탄탄한 수학적 기초위에 서있을 수 있다. 이런 이유로 공학 수학 시간에 스튀름–리우빌 이론을 배운다. 왜냐하면 스튀름–리우빌 이론을 통해 고유 함수의 무한 급수로 임의의 함수를 쉽게 표현할 수 있기 때문이다. 푸리에 급수와 같은 고유 함수의 무한 급수를 처음 보면 고유 함수를 무한히 더해서 임의의 함수를 표현하는 절차가 매우 신기해보인다. 그다음에는 책에서 맞다니까 무작정 고유 함수의 무한 급수 특성을 외우게 된다. 그런데 이렇게 해서는 발전이 없다. 자기 신념과 확신이 필요하다. 위의 증명을 따라올 수 있으면 푸리에 급수를 마음속으로부터 완벽히 이해하게 되고 더 나아가 스튀름–리우빌 미분 방정식이 만드는 고유 함수의 무한 급수 특성까지 알 수 있다.

식 (12)를 이용하면 $m$이 커질 때 무한 급수의 계수인 $a_m$의 특성을 유도할 수 있다. 식 (12)에서 고유치와 계수의 무한 급수는 반드시 수렴해야 하므로, 다음 관계가 성립한다.

                      (15)

따라서, $m$이 커질 때 $a_m$은 커지지 않고 항상 $\tau_a$의 속도로 작아진다.

푸리에 급수 전개처럼 식 (1)을 다음 적분으로 표현할 수 있다.

                     (16)

식 (16)은 어떤 연속 함수에 대해서도 성립하므로 $f(x)$를 상수 함수(constant function)라 생각하면 다음을 얻을 수 있다.

                     (17)

식 (16)과 (17), 디랙 델타 함수(Dirac delta function) 정의를 이용하면, 고유 함수로 만든 무한 급수를 델타 함수로 표현할 수 있다.

                     (18)

[그림 1] 불연속 함수(출처: wikipedia.org)

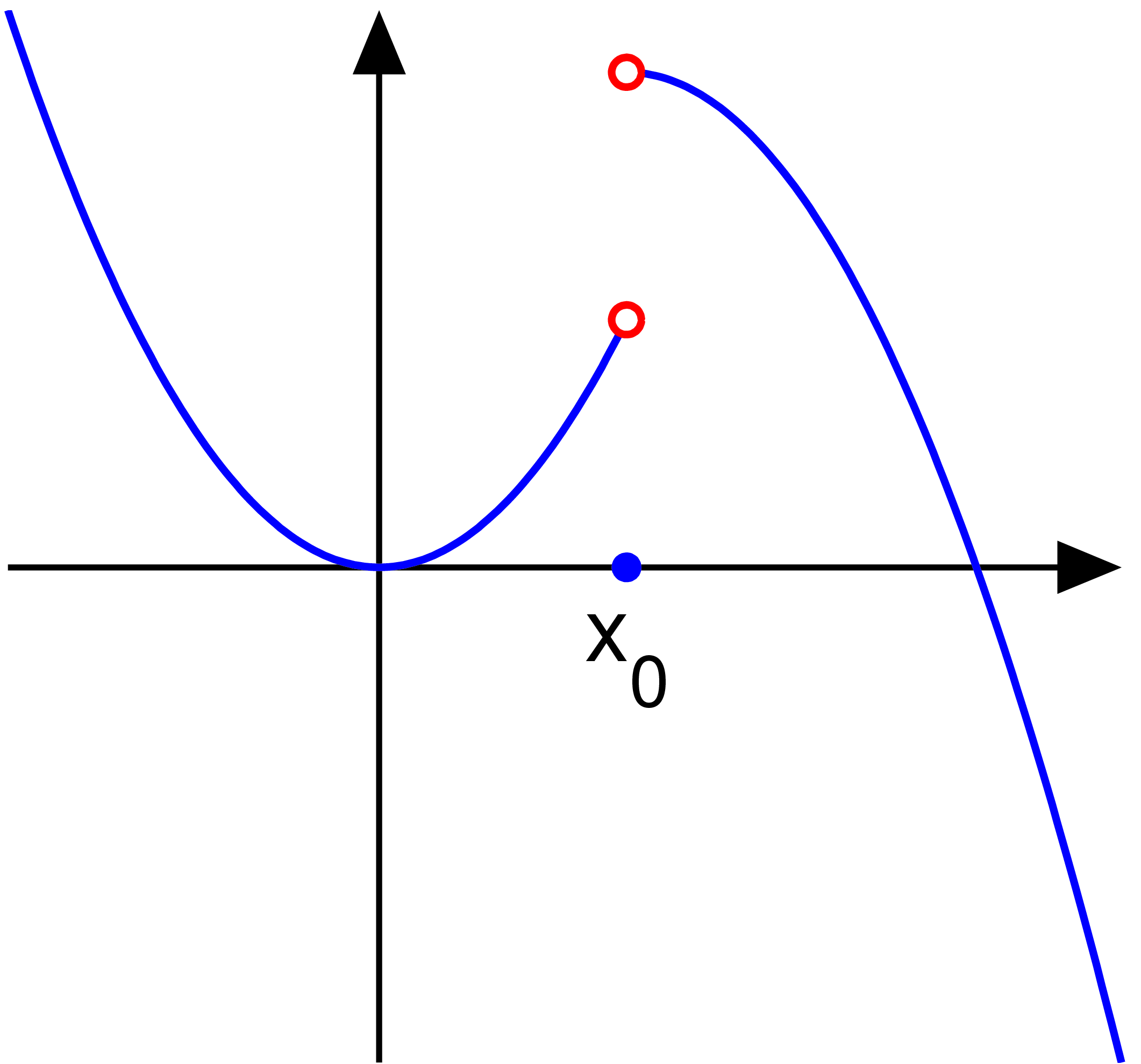
[그림 1]과 같은 불연속 함수(discontinuous function)를 고유 함수로 표현하면 어떻게 될까? 함수의 불연속성을 고유 함수로 표현할 수 있을까? 당연히 표현할 수 없다. 함수가 불연속인 점에서는 고유 함수의 무한 급수로 표현할 수 없다. 그렇다 하더라도 식 (1)이 틀렸다고 볼 수는 없다. 실제로는 고유 함수의 완비성을 아래와 같은 적분 형태로 표현하기 때문이다.

                     (19)

표현식이 적분이므로 어느 한 점에서 $f(x)$와 $S_M(x)$가 같지 않더라도 여전히 적분값은 0이다. 그러면, 불연속점에서는 고유 함수의 무한 급수가 어떤 값을 가지는가? 이를 이해하기 위해 불연속성을 아래처럼 연속성의 극한으로 생각한다.

                      (20)

여기서 $\Delta x$가 0으로 가면 우리가 원하는 불연속성이 얻어진다. 또한, 테일러 급수(Taylor series)로 인해 $\Delta x$가 아주 작을 때는 모든 함수 $f(x)$의 적절한 근사가 식 (20)이 된다. $\Delta x \ne 0$일 때에 함수 $f(x)$는 여전히 연속해서 식 (1)에 증명한 고유 함수의 완비성이 성립한다. 만약 $\Delta x$가 0으로 한없이 가까이 가면 $x$ $\approx$ $x_0$이므로, 식 (20)에 의해 고유 함수의 무한 급수는 $f(x_0)$ = $(f_r + f_l)/2$에 수렴한다. 즉, 불연속점에서는 좌극한($f_l$)과 우극한($f_r$)의 평균에 수렴한다. 조금 다른 각도로 보면 $\Delta x$가 아무리 바뀌더라도 함수값이 변하지 않는 고정점이 $x$ = $x_0$이며 고유 함수의 무한 급수는 고정점인 $f(x_0)$ = $(f_r + f_l)/2$로 수렴한다. 대충 생각하면 어떤 $\Delta x$에 대해서도 $f(x_0)$ = $(f_r + f_l)/2$를 만족해서 $\Delta x \to 0$인 경우에도 $f(x_0)$는 고정된다.

[참고문헌]

[1] W. O. Amrein, A. M. Hinz, D. B. Pearson, Sturm–Liouville Theory: Past and Present, Birkhäuser Basel, 2005.

[2] R. D. Costin, Completeness of the Eigenfunctions, Sturm–Liouville Theory, 2010. (방문일 2011-12-05)

[다음 읽을거리]
1. 고유치가 복소수인 스튀름–리우빌 이론