리만–스틸체스 적분(Riemann–Stieltjes Integral)

[경고] 아래 글을 읽지 않고 "리만–스틸체스 적분"을 보면 바보로 느껴질 수 있습니다.

1. 적분법의 의미

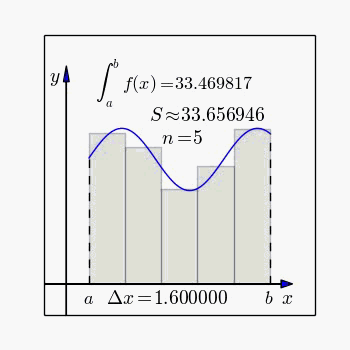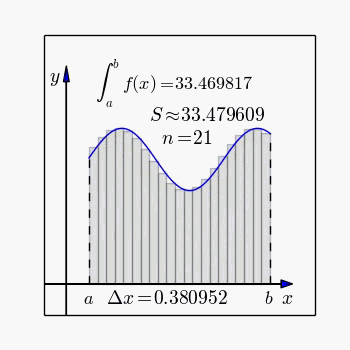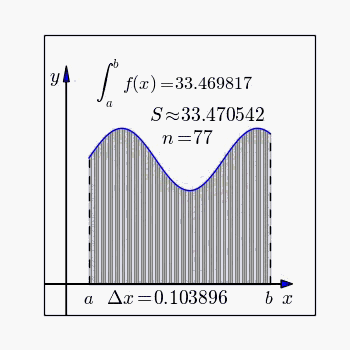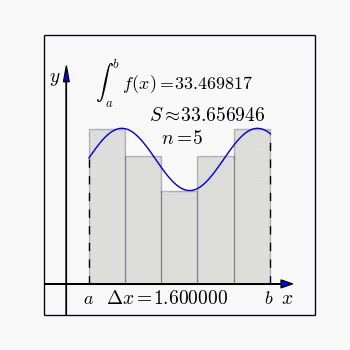
[그림 1] 리만 적분으로 정의하는 정적분(출처: wikipedia.org)

통상적인 정적분(定積分, definite integral)은 [그림 1]처럼 $x$축을 따라가면서 함수값 $f(x)$가 만드는 면적을 계산한다.

                  (1)

식 (1)을 더 확장하려면 어떤 방법을 택해야 할까? 고급 개념인 벡터(vector)를 적용해서 식 (1)을 선 적분(line integral)으로 만들 수 있다.

                  (2)

혹은 식 (2)에 도입한 벡터 개념을 버린 후, $x$를 대신하는 임의의 곡선 $g(x)$를 적분 변수로 두고 $f(x)$를 단순하게 정적분한다.

                  (3)

여기서 $dg(x)$는 $g(x)$의 미분소(differential), $g(x)$의 움직임을 결정하는 $x$는 단조 증가하거나 감소한다. 식 (3)과 같이 리만 적분(Riemann integral)을 일반화한 정적분은 리만–스틸체스 적분(Riemann–Stieltjes Integral)이라 한다. 리만–스틸체스 적분은 스틸체스Thomas Joannes Stieltjes(1856–1894)가 1894년스틸체스 38세, 조선 고종 시절에 제안했다. 리만 적분의 정의를 이용해서 리만–스틸체스 적분을 더 고상하게 표현할 수도 있다.

                  (4)

여기서 $x_n$은 정적분을 위해 구간 $[a, b]$를 나눈 점, $t_n$은 닫힌 세부 구간 $[x_{n}, x_{n+1}]$ 사이에 있는 임의점이다. 점 $x_n$이 단조 증가인 경우는 다음과 같은 순서 조건을 만족한다.

                  (5)

만약 $g(x)$ = $x$인 직선이라면, 리만–스틸체스 적분은 단순한 리만 적분이 된다. 식 (3)에는 $g(x)$의 미분소가 있으므로, 다음과 같이 $x$에 대한 적분으로 변형하기도 한다.

                  (6)

또한 부분 적분(integration by parts)을 이용해서 미분소 $dg(x)$를 $df(x)$로 바꿀 수도 있다.

                  (7)

여기서 $d[f(x)g(x)]$ = $g(x) df(x) + f(x) dg(x)$이다.

[다음 읽을거리]

1. 아벨의 적분 방정식

2. 오일러–매클로린 공식