1. 커패시터
2. 유전체의 비밀
3. 전송선 이론
4. 전압파의 반사 계수
안테나(antenna)를 설계하든 필터(filter)를 설계하든 기판 위에 RF(Radio Frequency) 소자를 설계하려면 먼저 사용하는 기판(substrate)의 특성을 알아야 한다. 기판의 두께는 자나 캘리퍼스(calipers)로 재면 되지만 유전 상수(dielectric constant) 혹은 비유전율(relative permittivity) 측정법은 금방 떠오르지 않는다. 유전율이 생기는 원인은 물질 내부에 있는 양성자와 전자가 분리되는 분극(polarization)이므로 양성자와 전자가 떨어지는 현상을 재면 되지만 너무 작은 영역에서 일어나는 일이라 이게 쉽지 않다. 그래서, 간접 측정법[1]을 사용하여 유전 상수를 측정하게 된다. 많이 쓰는 방법이 전기 용량(capacitance), 반사도(reflection coefficient) 혹은 공진 주파수(resonant frequency)를 잰다. 당연히 저주파에서는 전기 용량법이 많이 쓰이고 고주파에서는 반사도 방법이나 공진 주파수 방법이 자주 쓰인다.
[그림 1] 주파수에 대한 물의 유전 상수 변화(출처: [3])
유전 상수 측정에는 재미있는 일화가 있다. 맥스웰James Clerk Maxwell(1831–1879)이 1862년맥스웰 31세, 조선 철종 시절부터 빛도 전자파의 일종이라고 주장했을 때 거의 대부분의 물리학자로부터 많은 비난을 받았었다. 스코틀랜드 출신의 듣도 보도 못한 신출내기 물리학자의 주장을 혁신적으로 보는 학자는 거의 없었다. 이 신출내기가 기반으로 삼은 개념도 비웃음거리였다. 수학을 전혀 모르는 실험 물리학자 패러데이Michael Faraday(1791–1867)의 전기력선과 전기장의 개념을 이용했기 때문이다. 맥스웰의 개인적인 상황도 이 당시는 좋지 않았다[4]. 케임브리지 대학교(University of Cambridge)를 졸업하고 거의 바로 스코틀랜드 애버딘(Aberdeen, Scotland)의 매리셜 대학교(Marischal College)의 교수가 되고 결혼도 했다. 이때까지는 좋은 시절이었지만, 1860년맥스웰 29세, 조선 철종 시절에 대학 통합으로 교수직을 잃고[천하의 맥스웰이 1860년에는 구조 조정을 당했었다.] 에딘버러 대학교(University of Edinburgh)에 지원했으나 다시 떨어졌다. 겨우 신생 학교인 런던 국왕대학교(King's College London)에 다시 자리를 잡았다. 런던 국왕대학교에서 절치부심하며 1864년맥스웰 33세, 조선 고종 시절에 만든 멋들어진 결과가 맥스웰 방정식(Maxwell's equations)이다.[맥스웰 방정식과 관계된 정확한 날짜[7]: 논문 투고 1864년 10월 27일, 논문 공개 1864년 12월 8일, 논문 출판 1865년 1월] 이런 상황이었으니 주변 물리학자들이 맥스웰의 중대한 연구 결과에 주목하지 않았던 사실은 매우 당연해 보인다. 그 비난 중에서 가장 심각했던 과학적 사실이 물의 유전율이다[3], [9], [10]. 물의 유전 상수($\epsilon_r$)를 실온에서 재어보면 약 80 정도 나온다. 맥스웰은 빛도 전자파라고 했기 때문에 빛에 대한 굴절률(refractive index: 물은 약 1.33) $n$으로부터 물의 유전 상수[$\epsilon_r = n^2$]를 환산할 수 있다. 애석하게도 빛의 굴절률[$n = 1.33$]로 환산한 물의 유전 상수값은 80이 아니고 약 1.8 정도로 계산된다.[물의 유전 상수는 온도와 압력에 따라 달라지므로 근사치로 표현한다.] 이론값 기준으로 측정값이 몇 배도 아니고 40배 이상 차이가 난다. 자신의 방정식이 흔한 물의 특성도 예측하지 못했기 때문에, 맥스웰 방정식(Maxwell's equations)은 자기 고국인 영국에서도 버림받게 된다. 당시 주류였던 대(大)물리학자 켈빈William Thomson, Lord Kelvin(1824–1907)[온도 단위에 나오는 바로 그 아저씨]의 비판도 맥스웰에게는 큰 짐이었다. 켈빈은 너무나도 이상한 맥스웰의 방정식을 인정하지 않았다[5]: 밑도 끝도 없이 장(field) 개념을 소개하고 사원수(quaternion) 기반의 편미분 방정식(partial differential equation)을 20개나 쏟아내는 기괴한 맥스웰 방정식. 켈빈은 역학적 기반이 없이 수학적 상상에만 기반을 둔 이런 맥스웰 방정식을 혹독하게 비판했다[5]. 이런 상황 때문에 맥스웰 지지자는 소수였고 켈빈 지지자는 넘쳐났다. 이후 독일의 헤르츠Heinrich Hertz(1857–1894)가 1887년헤르츠 30세, 조선 고종 시절에 전자파 존재를 실험적으로 증명하여 맥스웰의 이론은 다시 주목을 받기 시작한다. 하지만 안타깝게도 이때는 맥스웰이 위암으로 죽은 후였다. 전자파 존재 증명은 켈빈에게도 맥스웰에게도 비극이었다. 켈빈이 그렇게 비판하고 무시했던 맥스웰의 이론이 켈빈[1907년에 사망] 살아 생전에 존재가 증명되었고, 맥스웰은 자신의 평생 역작이 빛을 보는 놀라운 광경을 보지 못하고 1879년맥스웰 48세, 조선 고종 시절에 사망했으니 말이다. 요즘은 맥스웰을 고민하게 했던 물의 유전율 변화 현상을 쉽게 설명할 수 있다. [그림 1]처럼 물은 주파수에 따라 유전 상수가 심하게 달라지기 때문이다. 물의 유전 상수가 약 80임은 DC에 가까운 저주파에서 측정했다는 뜻이다. 빛에 대한 유전 상수는 매우 높은 주파수에서 측정하므로 약 1.8이 나오게 된다.
1. 전기 용량 방법(capacitance method)
[그림 1.1] 커패시터의 구조(출처: wikipedia.org)
[그림 1.1]과 같이 구조가 아주 전형적인 커패시터를 하나 준비한다. 커패시터의 물리적 크기(길이 혹은 면적)은 잘 알고 있다고 가정한다.[∵ 물리적 특성은 자로 재면 된다.] 그 다음에 [그림 1.2]와 같은 LCR 계측기(LCR meter)를 이용해 커패시터의 전기 용량을 실험적으로 정확하게 측정한다. LCR 계측기는 부하 임피던스(load impedance)를 정밀하게 재는 측정 장비이다. LCR 계측기에 있는 LCR은 당연히 L(인덕터, inductor), C(커패시터, capacitor), R(저항, resistance)을 의미한다. 하지만 LCR 계측기는 소자의 저주파 특성[주로 kHz, 많아야 MHz]을 재는 장비이므로 GHz를 넘는 고주파는 LCR 계측기로 재지 못하고 아래 [그림 2.1]에 있는 회로망 분석기를 사용해야 한다.
[그림 1.2] LCR 계측기: Keysight(Agilent) E4980A(출처: keysight.com)
LCR 계측기가 없다면 커패시터의 충전과 방전 실험을 통해 오차가 크지만 값싼 방법으로 전기 용량을 잴 수도 있다. 따라서, 커패시터의 물리적 크기와 전기 용량을 알면 수치 해석 기법을 통해 커패시터에 채워진 물질의 유전 상수를 결정할 수 있다. 물리적 크기가 고정되면 유전 상수가 커질수록 전기 용량이 커지기 때문에 가능하다. 수치 해석 기법을 쓰기가 곤란하면 커패시터를 [그림 1.3]처럼 평행판으로 만들면 된다.
[그림 1.3] 평행판 커패시터(출처: wikipedia.org)
[그림 1.3]에 보인 평행판 커패시터의 전기 용량 공식은 단순하게 결정된다.
(1.1)
식 (1.1)에서 물리적 크기$(A, d)$와 전기 용량 $C$가 결정되면 유전율(permittivity) $\epsilon$이 정해진다.
(1.2)
유전 상수와 유전율은 식 (1.2)의 관계를 가지므로 유전 상수 $\epsilon_r$이 결정된다.
2. 반사도 방법(reflection coefficient method)
반사도 법[6], [8]은 [그림 2.1]에 소개한 회로망 분석기(network analyzer)를 사용하기 때문에 굉장히 정밀한 유전 상수 측정법이다. 또한 회로망 분석기는 LCR 계측기와는 다르게 GHz까지도 측정 가능하므로 고주파 측정의 핵심 장비이기도 하다.
[그림 2.1] 회로망 분석기(출처: wikipedia.org)
유전율 측정은 번거운 과정이기 때문에 [그림 2.2]와 같은 자동화된 측정법을 많이 사용한다[2]. 요즘 나오는 회로망 분석기는 이를 지원하기 위해 GPIB(General Purpose Interface Bus)나 네트워크 카드가 기본적으로 장착되어 있다.
[그림 2.2] 자동화된 유전율 측정 장치(출처: emtool.com)
회로망 분석기에 기하 구조가 단순한 부하[여기에 측정하고자 하는 유전체를 삽입: 그림 2.2에서는 동축선 측정기]를 연결하고 [그림 2.3]의 구성으로 반사도를 측정한다. 회로망 분석기는 [그림 2.4]처럼 매질의 불연속에 의해 생성되는 반사파를 재는 정밀한 측정 장비이다.
[그림 2.3] 전원과 부하가 있는 전송선 회로
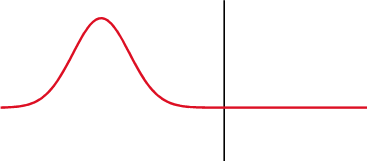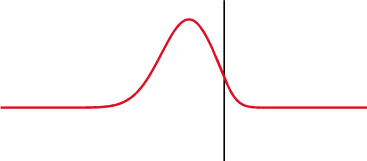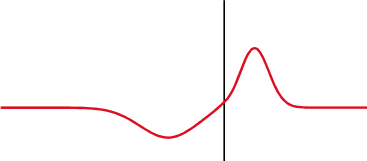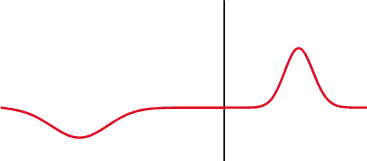
[그림 2.4] 파동의 반사와 투과(출처: wikipedia.org)
반사도가 측정되면 식 (2.1)에 의해 부하 임피던스(load impedance)를 알 수 있다. 부하의 유전율을 바꾸면 부하 임피던스가 바뀐다.
(2.1)
기하 구조가 알려졌기 때문에 유전율값을 바꾸어가면서 측정한 반사도와 수치 해석 기법으로 계산한 반사도가 최대한 같아지도록 한다.[이 방식은 그림 2.5처럼 역방향 문제(inverse problem)를 풀 때 주로 쓰는 방법이다.]
[그림 2.5] 유전율을 예측하는 알고리즘(출처: emtool.com)
[그림 2.5]의 알고리즘에 따라 측정한 반사도와 계산한 반사도의 오차가 가장 작은 유전율값을 답으로 예측한다[2]. 오차를 더 줄이기 위해 단일 주파수에 대해 측정하지 않고 넓은 주파수 범위에 대해 측정한다. 유전체를 장착할 수 있는 부하 구조는 도파관(waveguide)이나 동축선(coaxial cable)을 많이 사용한다.
3. 공진 주파수 방법(resonant frequency method)
유전율이 바뀌면 공진 주파수가 바뀌는 특성을 이용해 기판의 유전 상수를 결정한다. [그림 2.1]와 같은 회로망 분석기에 RF 필터[여기에 측정하고자 하는 유전체를 삽입]를 물리고 공진 특성을 측정한다. 공진 주파수가 측정되면 [그림 2.5]과 같이 유전율을 바꾸어가면서 측정한 공진 주파수와 수치 해석 기법으로 계산한 공진 주파수가 최대한 같아지도록 한다. 측정한 공진 주파수와 계산한 공진 주파수의 오차가 가장 작은 유전율값이 답이다. 이 방법은 공진 주파수만 찾기 때문에 반사도 법과는 다르게 넓은 주파수 범위를 측정할 필요는 없다.
[참고문헌]
[1] Measuring dielectric constant, Microwave Encyclopedia, 2008.
[2] 동축선 기반 유전율 측정장치 제어시스템, 이엠툴, 2010. (방문일 2011-10-21)
[3] T. Meissner and F. Wentz, "The complex dielectric constant of pure and sea water from microwave satellite observations," IEEE Trans. Geo. Rem. Sens., vol. 42, no. 9, pp. 1836–1849, Sep. 2004.
[4] L. Campbell and W. Garnett, James Clerk Maxwell with a Selection from his Correspondence and Occasional Writings and a Sketch of his Contributions to Science, Macmillan, 1882.
[5] K. Johnson, The Electromagnetic Field, James Clerk Maxwell - The Great Unknown, 2002.
[6] Basics of measuring the dielectric properties of materials, Application Note, Agilent. (방문일 2023-09-30)
[7] G. Pelosi, "A tribute to James Clerk Maxwell on the 150th anniversary of his equations (1864–2014)," IEEE Antennas Propagat. Mag., vol. 56, no. 6, pp. 295–298, Dec. 2014.
[8] M.-S. Park, J. Cho, S. Lee, Y. Kwon, K.-Y. Jung, "New measurement technique for complex permittivity in millimeter-wave band using simple rectangular waveguide adapters," J. Electromagn. Eng. Sci., vol. 22, no. 6, pp. 616–621, Nov. 2022.
[9] A. De Ninno, E. Nikollari, M. Missori, F. Frezza, "Dielectric permittivity of aqueous solutions of electrolytes probed by THz time-domain and FTIR spectroscopy," Phys. Lett. A, vol. 384, no. 34, 2020, art. no. 126865.
[10] Attenuation Due to Clouds and Fog, Recommendation ITU-R P.840-9, Aug. 2023.
(3)
(4)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)
(27)
(28)
(29)
(30)
(31)
(32)
(33)
(1)
(2)
(3)
(4)
(6)
(7)
(10)
(22)
(24)
