
(2b)
여기서 $y(\xi x)$는 $y(x)$의 변수 치환이다. 우리가 베셀 함수를 공부하는 이유는 원통 좌표계
(circular cylindrical coordinate system) 관련 문제를 풀 때 빠지지 않고 항상 출현하기 때문이다. 즉 물체의 모양이 원통이면 당연히 미분 문제의 좌표계를 원통 좌표계로 택한다. 그러면 이 미분 방정식의 해는 베셀 함수의 선형 결합으로 표현된다.
하지만 베셀 함수를 컴퓨터 코드로 직접 구현하기는 매우 어렵기 때문에, 주로 수치 해석 전문가가 작성한 결과를 이용해서 베셀 함수를 계산한다. 차수(order, $n$ or $\nu$)가 실수이고 입력 변수(argument, $x$ or $z$)는 실수 혹은 복소수인 베셀 함수의 계산은 [5]를 주로 사용한다. 차수가 복소수로 확장된 베셀 함수의 코드는 [6]을 참고할 수 있다. 또한 베셀 함수를 수치 계산하는 알고리즘(algorithm or algorism)은 아주 예전에 만들어졌기 때문에 주로 포트란(Fortran: IBM 수학 공식 번역 체계, The IBM Mathematical Formula Translating System)으로 작성되었다.
[음의 차수]
 (1.1)
(1.1)
 (1.2)
(1.2)
[증명]
식 (1.1)을 증명하기 위해
일반화된 제1종 베셀 함수(Bessel function of the first kind)를 생각한다.

(1.3)
식 (1.3)에 $\nu$ = $-n$을 대입하여 정리하면 다음을 얻는다.

(1.4)
여기서
감마 함수(gamma function)의 입력에 음의 정수
[$m-n+1 \le 0$]가 들어가면 무한대가 되는 성질을 이용한다.
[∵ 감마 함수의 그래프를 보면 음의 정수에서 감마 함수의 크기가 무한대 됨을 볼 수 있다. 혹은 식 (6.4)의 오일러 반사 공식을 봐도 음의 정수에서 감마 함수가 발산함을 증명할 수 있다.] 식 (1.2)는 다음에 제시한
제2종 베셀 함수(Bessel function of the second kind)의 정의를 이용하면 쉽게 증명된다.

(1.5)
식 (1.5)에서 $\nu$ = $-n$을 대입하면 다음을 얻을 수 있다.

(1.6)
______________________________
[음의 입력 변수: 패리티 혹은 동등성(parity)]
 (1.7)
(1.7)
 (1.8)
(1.8)
베셀 함수를
무한 급수로 표현한 식에 음의 입력 변수를 대입하여 증명한다. 제2종 베셀 함수 경우는 무한 급수 외에 로그 함수가 있으므로, $\log(-|x|)$ = $\log(|x|) + i \pi$로 인해 식 (1.8)과 같은 결과가 나온다.
______________________________
[한켈 함수(Hankel function)에 대한 음의 입력 변수: 패리티 혹은 동등성(parity)]
[증명]
한켈 함수의 정의에 식 (1.7)과 (1.8)을 대입하여 증명한다. 예를 들면 식 (1.9)의 증명은 다음 절차를 거친다.

(1.11)
______________________________
[베셀 함수의 관계] 
(1.12)

(1.13)
[증명]
 (1.14)
(1.14)
마찬가지 방법으로 식 (1.13)의 둘째식도 유도한다.
______________________________
[일반화된 음의 차수]

(1.15)
[증명]식 (1.13)에서 $\nu$에 $-\nu$를 치환해서 증명한다.
______________________________

(1.16)
[증명]식 (1.12)에 식 (1.15)를 대입해서 유도한다.
______________________________
만약 식 (1.16)의 차수 $\nu$가 정수라면, 식 (1.16)은 식 (1.1)과 (1.2)로 간략화된다.

(1.17)
[증명]식 (1.16)을 식 (1.17)의 좌변에 대입해서 양의 차수로 바꾸어서 정리한다.
______________________________
식 (1.17)은 $d/dx$ 혹은 $d/dy$를 적용해도 성립한다.
[해석적 연속(analytic continuation)]

(1.18)
여기서 $m$은 정수, $z$는 복소수이다.
[증명]______________________________
제1종 베셀 함수 $J_\nu (z)$의 차수 $\nu$가 정수가 아닌 실수라면, $z^\nu$로 인해 음의 실수축에
가지 자름(branch cut)이 생긴다. 우리가 계산할 때는 가지 자름을 피하므로, 음의 실수축은 $J_\nu (z)$의 정의역에서 보통 제외한다. 하지만 식 (1.18)의 $e^{m \pi i}$처럼 원점에 대한 회전 회수를 명확히 하면, $z$ = $0$을 제외한 모든 복소 영역에서 $J_\nu (z)$를 해석적이게 할 수 있다. 즉 $z$가 음의 실수축을 넘어갈 때, 식 (1.18)에 기반해 $J_\nu (z)$를 다음과 같이 바꾸면 함수값은 계속 연속적으로 변하게 된다.
 (1.19)
(1.19)
여기서 임의로 작은 양수 $\delta$에 대해 $\operatorname{arg}(z)$ = $\pi-\delta$와 $\pi+\delta$는 식 (1.19)의 좌변과 우변으로 각각 계산하며, 식 (1.19)의 우변에서 $z$의 편각이 $\pi$를 초과하면 $z e^{-2 \pi i}$의 편각은 $-\pi$부터 다시 시작한다. 이러한 복소 함수의 체계적인 정의역 확장을
해석적 연속(analytic continuation)이라 한다.

(1.20)
[증명]식 (1.14)처럼 제2종 베셀 함수의 정의에 식 (1.18)을 대입해서 식 (1.20)을 유도한다.
______________________________
식 (1.18)과 (1.20)의 차수 $\nu$가 정수, $m$ = $1$이고, $z$가 양의 실수라면, 식 (1.18)과 (1.20)은 각각 식 (1.7)과 (1.8)이 된다.
 (1.21)
(1.21)
[증명]식 (1.13)의 첫째식에 식 (1.5)와 (1.18)을 대입해서 정리한다.

(1.22)
마찬가지 방식으로 식 (1.21)의 둘째식을 증명한다.
______________________________
식 (1.21)의 첫째식과 둘째식에 $m$ = $1$과 $-1$을 각각 대입해서 다음처럼 단순화된 관계식을 얻는다.
 (1.23)
(1.23)
식 (1.23)의 첫째식에서 $\nu$가 정수이고 $z$가 양의 실수인 경우는 식 (1.9)가 된다. 하지만 식 (1.23)의 둘째식은 식 (1.10)이 되지 않는다. 이는 식 (1.23)에 있는 $e^{-\pi i}$ 때문이다. 다시 말해 $e^{-\pi i}$가 의미하는 음의 실수축의 약간 아래에서 계산한 결과는 식 (1.23)의 둘째식이지만, 식 (1.10)은 음의 실수축에서 약간 위인 $e^{\pi i}$에서 정의하기 때문이다.
[켤레 복소수(complex conjugate)]
 (1.24)
(1.24)

(1.25)
식 (1.3)에 제시한 제1종 베셀 함수의 무한 급수 표현식을 이용해서 식 (1.24)의 첫째식을 증명한다. 여기서
감마 함수의 켤레 복소수 관계를 이용한다. 식 (5.3)에 있는 제2종 베셀 함수의 정의에 켤레 복소수를 적용해서 식 (1.24)의 둘째식도 증명한다.
식 (1.24)에 의해 식 (1.25)도 자연스럽게 성립한다. 예를 들어, $\left[H_\nu^{(1)}(z) \right ]^*$ = $J_{\nu^*}(z^*) - i N_{\nu^*}(z^*)$ = $H_{\nu^*}^{(2)}(z^*)$처럼 증명이 가능하다
______________________________
2. 함수 표현식(function representation)
[푸리에 변환]

(2.1)
[증명]
______________________________
[삼각 함수의 거듭제곱]

(2.2)
여기서 $\nu > -1/2$이다.[$\because$ 유도 과정에 베타 함수의 적분 표현식을 사용하기 때문에]
[증명]

(2.3)

(2.4)
식 (2.4)를 식 (1.3)에 대입하여 정리해보자[1].

(2.5)

(2.6)

(2.7:
삼각 함수의 합차 공식)
식 (2.6)과 (2.7)을 식 (2.5)에 대입하면 다음을 얻는다[1].

(2.8)
식 (2.2)처럼 적분 구간을 확장하려면, $\theta$ = $(0, \pi/2)$에 대해 $\phi$ = $\pi - \theta$로 변수 치환하면 된다.
______________________________
[베셀의 적분(Bessel's integral)]
여기서 $n$은 정수이다. 피적분 함수에 코사인이 들어간 식 (2.9a)의 적분은 식 (5.2)에 제시되어 있다.
[증명]
차수 $n$ = $0$인 경우는 식 (2.2)를 통해 증명 가능하다.

(2.10)
차수 $n$ = $1$인 경우는 식 (5.6)을 이용할 수 있다.

(2.11)
다음으로 식 (2.9a)가 식 (5.1)의 재귀 관계를 만족함을 보인다.

(2.12)
식 (2.12)에 식 (2.10)과 (2.11)을 대입하면 모든 $n$에 대해 식 (2.9a)의 첫째식이 성립함을 증명할 수 있다. 식 (2.9a)의 둘째식은 식 (2.9a)의 첫째식에서 적분 구간을 $(-\pi, 0)$, $(0, \pi)$로 나누고 변수 치환하면 쉽게 증명된다.
이번에는 식 (2.9a)로 만든 식 (3.1a)의 야코비–앙어 전개(Jacobi–Anger expansion)에 바탕을 두고, 식 (3.1a)의 둘째식에 푸리에 급수의 직교성을 적용함으로써 식 (2.9b)를 유도한다. 식 (2.9b)의 $n$에 $-n$을 대입한 식과 식 (2.9b)를 더하거나 빼서 식 (2.9c)도 증명한다.
______________________________
[생성 함수에 대한 적분]

(2.13)
여기서 $n$은 정수이며 폐경로 $c$는 $t$ = $0$을 감싼다.
[증명]
식 (3.7)의
생성 함수(generating function)에 복소 함수론의
유수 정리(留數定理, residue theorem)를 적용하면 증명된다.
______________________________
[그림 2.1] 한켈 경로 $\mathcal{H}$의 원점 대칭 경로 $\mathcal{C}$ = $-\mathcal{H}$
[쉴레플리의 적분(Schläfli's integral)] 
(2.14)
여기서 적분 경로 $\mathcal{C}$ = $-\mathcal{H}$는 [그림 2.1]에 제시된 대로
한켈 경로(Hankel contour) $\mathcal{H}$에 원점 대칭이다.
식 (2.14)의 우변에 있는 적분을 다음처럼 변수 치환해서 쉴레플리의 제1 적분(Schläfli's first integral)을 만든다[2].
 (2.15)
(2.15)
식 (2.15)에 있는 경로 적분
(contour integral)을
테일러 급수 전개(Taylor series expansion)하면, 다음 결과를 얻는다[2].
 (2.16)
(2.16)
여기서 복소 적분의 경로를 $\mathcal{C}$에서 $\mathcal{H}$로 바꾼다. 적분 경로 $\mathcal{H}$는
한켈 경로이다. 식 (2.16)에 있는 $f(w)$를 식 (2.15)에 대입해 식 (1.3)과 비교하면 증명이 끝난다.
______________________________
식 (2.13)과 (2.14)를 비교해 보면, 정수 $n$이 실수 $\nu$로 치환된다. 정말 이렇게 단순할까? 우리는 아는 만큼만 볼 수 있다. 이 두 식에서 중요한 차이는 적분 경로 설정이다. 한켈 경로로 적분 경로를 선택하면, 베셀 함수의 정의에 나오는
감마 함수(gamma function)의 역수를 복소 적분으로 쉽게 표현할 수 있다. 즉, 복소 적분이란 새로운 틀로 베셀 함수를 바라보는 방법이 식 (2.14)이다.


(2.17)
[증명]
식 (2.14)와 [그림 2.1]에 있는 적분 경로를 다음과 같이 바꾸어본다.

(2.18)
식 (2.18)의 마지막 적분은 변수를 치환하여 다음처럼 증명한다.

(2.19)
______________________________
[그림 2.2] 한켈 경로의 원점 대칭 경로 $\mathcal{C}$와 관련된 사각형 경로 $\mathcal{R}$
[쉴레플리–좀머펠트 적분(Schläfli–Sommerfeld integral)] [4]
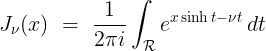
(2.20)
여기서 사각형 경로 $\mathcal{R}$은 [그림 2.2]와 같다.
[증명]식 (2.14)에 바탕을 두고 $t$ = $e^w$라고 변수 치환한다. 그러면 [그림 2.1]에 나온 $\mathcal{C}$는 사각형 경로 $\mathcal{R}$로 바뀌고 식 (2.14)도 아래와 같이 변형된다.
 (2.21)
(2.21) ______________________________
식 (2.20)은 쉴레플리Ludwig Schläfli(1814–1895)가 가장 처음에 만든 적분이며, 베셀의 적분을 일반화한 식 (2.17)은 그 다음에 유도되었다. 당연하지만 식 (2.20)의 적분 구간을 [그림 2.2]로 선택해서 식 (2.17)을 쉽게 증명할 수 있다.
 (2.22)
(2.22)
실수가 정의역인 베셀 함수의 적분 표현식에서 실수 $x$ 대신 복소수인 $z$를 치환해서 정의역을 복소수 영역으로 손쉽게 확장할 수 있다. 다만 적분 자체가 수렴해야 하므로, 식 (2.20)에 의해 $\Re[z] > 0$ 혹은 $|\arg(z)| < \pi/2$인 조건이 반드시 필요하다.
 (2.23)
(2.23)
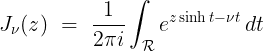 (2.24)
(2.24)
복소수 $z$에 대한 편각의 절대값이 $\pi/2$가 되면, 새로운 조건이 필요하다. 식 (2.24)에서 $z \sinh t$는 감쇠를 주지 못하므로, $\Re[\nu] > 0$이란 수렴 조건을 추가해야만 적분이 잘 수렴한다. 즉, 순허수 조건인 $\arg(z)$ = $\pm \pi/2$라면, 쉴레플리 적분의 수렴 조건은 $\Re[\nu] > 0$이 된다.
[그림 2.3] 한켈 경로의 원점 대칭 경로 $\mathcal{C}$의 여러 가지 변형
식 (2.15)를 복소수로 확장할 때에 필요한 조건은 무엇일까? 먼저 $u$ = $zt/2$로 변수 치환해서 식 (2.15)를 복소 영역으로 확대한 결과는 다음과 같다.
 (2.25)
(2.25)
여기서 식 (2.14)에 나온 원래 경로인 $\mathcal{C}$는 원점을 제외하고 $\Re[t] < 0$을 만족하도록 [그림 2.3]처럼 자유롭게 변형할 수 있고, 식 (2.25)의 새로운 $\mathcal{C}$는 $u$ = $zt/2$에 따라 복소 평면 상에서 회전한다. 식 (2.25)의 적분 경로를 이해하기 위해 적분 변수 $u$가 움직이는 특성을 상상한다. 예를 들어, $\arg(z) \approx \pi/2$라면, [그림 2.3]의 왼쪽 경로를 $t$의 $\mathcal{C}$로 택해서 $\Re[u] < 0$이 되도록 할 수 있다. 반대로 $\arg(z) \approx -\pi/2$가 되더라도 [그림 2.3]의 오른쪽 경로에 의해 여전히 $\Re[u] < 0$을 만족한다. 또한 변수 치환해서 만든 식 (2.25)에 등장하는 적분의 수렴성은 $e^u$가 결정하고 $z$와는 상관이 없어진다. 즉, 원점을 제외하고 $\Re[u] < 0$이 되도록 적분 경로 $\mathcal{C}$를 잘 선택하는 한, 식 (2.25)는 $z$의 편각에 관계없이 언제나 수렴한다. 결국 식 (2.25)는 식 (2.23)보다 더 일반화되기 때문에, 여러 가지 베셀 함수의 문제를 풀 때 매우 유용하다. 예를 들어,
변형 베셀 함수(modified Bessel function)의 적분 표현식을 만들 때에 식 (2.25)는 중요한 출발점이 된다.
3. 야코비–앙어 전개(Jacobi–Anger expansion)
야코비–앙어 전개(Jacobi–Anger expansion)는 복소 지수 함수와 제1종 베셀 함수를 연결하는 매우 중요한 공식이다. 야코비
Carl Gustav Jacob Jacobi(1804–1851)는 타원 함수
(elliptic function),
야코비 행렬(Jacobian) 등으로 워낙 유명해서 익숙한 이름이지만, 앙어
Carl Theodor Anger(1803–1858)는 조금 생소하다. 수학자 겸 천문학자인 앙어는 베셀 함수를 일반화시킨 베셀
Friedrich Wilhelm Bessel(1784–1846)의 제자이다. 그는 베셀이 천문대장인 쾨니히스베르크 천문대
(Königsberg Observatory)에서 훈련을 받았고, 이후에 스승의 모범을 따라 천문학자로서 천문학과 수학을 잘 발전시켰다.
[야코비–앙어 전개] 
(3.1a)

(3.1b)
식 (2.9a)에 있는 베셀의 적분은
푸리에 급수(Fourier series)에서 계수를 구하는 과정과 같다. 따라서, 식 (2.9a)를 푸리에 급수 관점으로 쓰면 식 (3.1a)의 첫째식을 얻을 수 있다. 식 (3.1a)의 첫째식에 있는
사인 함수(sine function)를 코사인 함수
(cosine function)로 바꾸면 식 (3.1a)의 둘째식이 얻어진다. 다음 단계로 식 (3.1a)의 둘째식을 $x, \theta$에 대해 각각 편미분해서 식 (3.1b)를 유도한다.
______________________________
식 (3.1a)의 둘째식을 활용하면 다음 적분을 얻을 수 있다. 아니면 식 (2.9a)의 첫째식을 변수 치환하면 된다.

(3.2)
야코비–앙어 전개와
베셀 함수의 점근식(asymptote of Bessel function)을 이용하면
균일 평면파(uniform plane wave)를
디랙 델타 함수(Dirac delta function)와 연결시킬 수 있다.

(3.3)
식 (3.3)에서 두 개의 디랙 델타 함수가 출현하는 이유는 균일 평면파의 특징 때문이다. 원점을 기준으로 보면 $\phi$ = $180^\circ$ 방향에서 평면파가 원점으로 들어와서 $\phi$ = $0^\circ$ 방향으로 평면파가 빠져나간다. 이 상황을 수학식으로 표현한 결과가 식 (3.3)이다. 식 (3.3)을 변형하면, 임의각인 $\phi$ = $180^\circ + \phi_0$에서 들어와서 $\phi$ = $\phi_0$로 빠져나가는 평면파는 다음처럼 표현된다.
 (3.4)
(3.4)
식 (3.4)를 한켈 함수(Hankel function)로 다시 표현하면, 평면파와 한켈 함수의 수학적 관계를 증명할 수 있다.  (3.5)
(3.5)

(3.6)
여기서 $0 \le \phi \le \pi$이다.
[생성 함수(generating function)]

(3.7)
오일러의 공식(Euler's formula)을 이용해 식 (3.1)의 사인 함수를 다음처럼 치환하면, 베셀 함수의
생성 함수(generating function)를 만들 수 있다.

(3.8)
식 (3.7)에서 $t$의 크기가 $1$이 아닌 경우는 어떻게 증명할까? 증명을 위해서는
복소 함수론의
로랑 급수(Laurent series)를 이용해야 한다. 식 (3.7)의 좌변을 $t$에 대해 로랑 급수 전개해본다. 하지만 실제로 할 필요는 없다. 식 (3.8)이 $|t|$ = $1$인 경우에 성립하기 때문에, 해석 함수의 성질에 의해 $|t| \ne 1$인 영역에서도 식 (3.7)은 타당하다. 물론 특이점 $t$ = $0$은 제외한다.
______________________________
[아벨의 항등식(Abel's identity)] 
(4.1)

(4.2a)

(4.2b)

(4.3a)

(4.3b)
여기서
함수 행렬식(Wronskian)은 다음과 같이 정의한다.

(4.4)
[증명]
베셀 함수의 차수
(order)를
고유치(eigenvalue)로 놓고 다음에 제시한
아벨의 항등식을 적용한다.
 (4.5)
(4.5)
여기서 $p(x)$ = $x$이다. 아벨의 항등식에서 필요한 상수는 보통 $x$ = $0$ 혹은 무한대로로 가는 극한을 택해서 결정한다. 예를 들어, 식 (4.1)의 증명에 필요한 상수는 다음과 같이 계산한다.

(4.6)
식 (4.2a)도 식 (4.6)과 비슷하게 상수를 정한다.
 (4.7)
(4.7)
식 (4.3a)는 $W[J_\nu(x), J_\nu(x)]$ = $0$과 식 (4.1)로 유도한다. 식 (4.3a)와 식 (4.1)을 조합해서 식 (4.2b)도 증명한다.
______________________________
식 (4.1)–(4.3)을 종합해서 더욱 일반화한 함수 행렬식을 도출할 수 있다.

(4.8a)

(4.8b)
여기서 $a,b,c,d$는 마음대로 선택하는 상수, $Z_\nu(\cdot), B_\nu(\cdot)$는 임의의 제$\nu$차 베셀 함수이다. 식 (4.8)은 선형 결합된 베셀 함수의 함수 행렬식은 단독 함수간 함수 행렬식의 상수배임을 보여준다.
5. 재귀 관계(recurrence relation)
[베셀 함수의 합]

(5.1)
여기서 $Z_\nu (x)$는 임의의 베셀 함수[$J, N, H$]이다.
[증명]
먼저
제1종 베셀 함수(Bessel function of the first kind)에 대해 다음을 증명한다.

(5.2)
또한
제2종 베셀 함수(Bessel function of the second kind)는 다음으로 정의된다.

(5.3)
식 (5.3)을 이용해 식 (5.1)의 관계식에 적용한다.

(5.4)
한켈 함수(Hankel function)는 다음처럼 정의되므로, 식 (5.2)와 (5.4)를 아래식에 대입하면 식 (5.1)이 성립함을 알 수 있다.

(5.5)
______________________________
[베셀 함수의 미분]

(5.6)
여기서 $Z_\nu (x)$는 임의의 베셀 함수[$J, N, H$]이다.
[증명]
증명 방법은 식 (5.1)과 동일하다.
제1종 베셀 함수(Bessel function of the first kind)에 대해 식 (5.6)을 적용하면 다음과 같다.

(5.7)
제2종 베셀 함수(Bessel function of the second kind)와
한켈 함수(Hankel function)에 대해서도 식 (5.4)와 유사하게 증명할 수 있다.
______________________________

(5.8)
[증명]식 (5.6)에 식 (5.1)을 대입해서 증명한다.
______________________________

(5.9)
[증명]조건 $Z_\nu (x)$ = $0$을 식 (5.1)에 대입해서 $Z_{\nu-1}(x)$ = $-Z_{\nu+1}(x)$를 얻는다. 이 결과를 다시 식 (5.6)에 넣으면 식 (5.9)가 유도된다.
______________________________
식 (5.9)에 따라 베셀 함수의 미분은 차수가 바뀐 베셀 함수로 쉽게 계산된다. 하지만 베셀 함수의 함수값 $Z_\nu (x)$는 꼭 0이란 조건이 필요하다.
6. 특정값(specific value)과 극한(limit)
[점 $x$ = $0$의 극한]

(6.1)

(6.2)
식 (1.3)에서 $m$ = $0$만 택하면 식 (6.1)이 증명된다. 식 (6.2)의 첫째식은
차수가 0인 제2종 베셀 함수의 $x$ = $0$에 대한 극한을 취해서 유도한다. 식 (6.2)의 둘째식 증명을 위해서는 식 (5.3)을 이용해야 한다. 차수가 $\nu > 0$인 경우의 극한은 다음과 같다.

(6.3)
식 (6.3) 증명에 아래에 있는
오일러의 반사 공식(Euler's reflection formula)을 이용한다.

(6.4)
______________________________

(7.1)

(7.2)
[증명]
식 (1.16)과 (1.15)를 각각 $\nu$에 대해 미분한 후, $\nu$ = $n$을 대입해서 식 (7.1)과 (7.2)를 각각 증명한다.
______________________________
음의 차수 미분이 가진 재미있는 성질은 제1종과 제2종 베셀 함수가 함께 나오는 점이다. 예를 들어, $J_{-n}(x)$를 미분하면 특성이 다른 $N_n(x)$가 섞여서 나온다. 식 (7.1)의 첫째식은 식 (1.5)와도 연결된다. 또한 베셀 함수의 차수가 식 (1.1)이나 (1.2)의 성질이 있다고 해서 양과 음의 차수 미분도 $(-1)^n$이 곱해지는 단순 관계라고 오해하면 안된다. 식 (7.1)에서 보듯이 양과 음의 차수 미분 사이의 관계는 제1종과 제2종 베셀 함수를 추가로 가져야 한다. 예시로 보면, 제1종 베셀 함수에 대한 양과 음의 차수 미분은 다음처럼 연결된다.

(7.3)
이와 같이 베셀 함수의 차수 미분은 쉽사리 정복하기 어려운 개념이다. 현재까지도 차수 미분은 닫힌 형태나 깔끔한 급수해 등이 알려지지 않고 있다. 다만 $n$ = $0$인 특별한 경우에는 차수 미분이 베셀 함수 형태로 매우 쉽게 표현된다.
 (7.4)
(7.4)

(7.5)
[증명]
차수 $n$ = $0$ 근방에서는 양이든 음이든 차수 미분은 동일하다. 차수 미분의 동일 조건을 식 (7.1)에 대입해서 식 (7.4)를 유도한다.
 (7.6)
(7.6)
식 (7.5)는 식 (7.4)를 조합해서 간단하게 증명할 수 있다.
______________________________
식 (7.1)과 거의 동일하게 식 (7.4)처럼 차수 미분을 하면, 제1종과 제2종 베셀 함수가 서로 교환된 공식이 깔끔하게 얻어진다.
8. 부정적분(indefinite integral)

(8.1)
여기서 $Z_m (\cdot)$과 $B_n(\cdot)$는 각각 임의의 제$m$차 및 제$n$차 베셀 함수
[$J, N, H$], $(\cdot)'$는 입력 변수
(argument)에 대한 미분, $C$는 적분 상수, $W(f, g)$는
함수 행렬식(Wronskian)이다.
[증명]
베셀 함수 $Z_m(x)$를 만드는 식 (2a)에 $B_n(x)$를 곱한 미분 방정식을 하나 만든다. 베셀 함수 $Z_m(x)$와 $B_n(x)$를 서로 바꾼 미분 방정식도 만든다. 이 두 식을 서로 빼주어 적분하면 식 (8.1)이 증명된다.
______________________________
식 (8.1)에서 $n$ = $\pm m$인 경우는
로피탈의 정리(L'Hopital's rule)를 써서 다음처럼 정리한다.

(8.2)
여기서 $dZ_m(x)/dm$은 차수에 대한 베셀 함수의 미분이다.
[제1 롬멜 적분(the first Lommel integral)]

(8.3)
여기서 $Z_m (\cdot)$과 $B_m(\cdot)$은 서로 다른 임의의 제$m$차 베셀 함수[$J, N, H$], $(\cdot)'$는 입력 변수(argument)에 대한 미분이다.
[증명]
식 (8.3)의 둘째 줄은 식 (8.1)과 비슷하게 증명한다. 식 (8.3)의 셋째 줄은 둘째 줄에 식 (5.8)을 대입해서 유도한다.
______________________________
[제2 롬멜 적분(the second Lommel integral)]

(8.4a)

(8.4b)
[증명]
식 (8.2)처럼 식 (8.3)의 둘째 줄에 대해 로피탈의 정리를 적용해서 식 (8.4a)를 얻는다.
 (8.5)
(8.5)
비슷한 방식으로 식 (8.3)의 셋째 줄에 로피탈의 정리를 써서 식 (8.4b)도 유도한다.
______________________________
 (8.6a)
(8.6a)
 (8.6b)
(8.6b)
여기서 $\lambda$는 적절한
고유치(eigenvalue)이다. 각 미분 방정식에
자기 수반성(自己隨伴性, self-adjointness) 연산을 적용해서 정리한다. 그러면 식 (8.1)과 (8.3)이 간단하게 도출된다.
 (8.7)
(8.7)

(8.8a)

(8.8b)
여기서 $W(u, v)$는
함수 행렬식(Wronskian), 식 (8.8a)와 (8.8b)를 위한 $y_1, y_2$는 각각 $Z_m(x), B_n(x)$와 $Z_m(\zeta \rho), B_m(\beta \rho)$이다.
[도함수의 제1 롬멜 적분(the first Lommel integral of derivatives)]

(8.9)
[증명]
도함수의 적분에
부분 적분(integration by parts)을 적용해서 아래와 같이 정리한다.
 (8.10)
(8.10) ______________________________
만약 $m$ = $0$이거나 $\zeta$ = $\beta$라면, 식 (8.2)와 (8.3)을 사용해서 식 (8.9)를 닫힌 형태로 표현할 수 있다. 하지만 그외 나머지 경우는 식 (8.9)의 마지막에 나타난 적분으로 인해 수치 적분을 피할 수 없다.
9. 정적분(definite integral)
[베셀 함수의 직교성]

(9.1)
여기서 $j_{\nu, m}$은 제$\nu$차 제1종 베셀 함수의 제$m$번 영점(zero), $J_\nu (j_{\nu, m})$ = $0$이다.
[증명]
조건 $J_\nu (j_{\nu, m})$ = $0$을 고려해서 식 (8.4a)를 정리하면 식 (9.1)의 둘째식을 얻는다. 이 둘째식에 식 (3.9)를 대입해서 다시 셋째식도 유도한다.
______________________________
식 (9.1)은 제1종 베셀 함수의 직교성(直交性, orthogonality)이라 부른다.

(9.2)
[증명]
식 (3.2)에 $n$ = $0$을 대입해서 적분 구간을 $[0, \pi]$로 바꾼다.
 (9.3a)
(9.3a)
피적분 함수 $\sin(x cos \theta)$는 구간 $[0, \pi]$에서 기함수이므로 적분값은 0이 되므로, 식 (9.2)와 같은 형태로 바꾸고 $t$ = $\cos \theta$로 변수 치환한다.
 (9.3b)
(9.3b) ______________________________
식 (9.2)의 피적분 함수는 $x$ = $\pm 1$에서 특이점을 가지지만, 적분값은 깔끔하게 계산된다.
[표 10.1] 제1종 베셀 함수의 영점 특정값: $J_\nu (j_{\nu, s})$ = $0$
| $j_{\nu, s}$ | $J_0(x)$: $\nu$ = 0 | $J_1(x)$: 1 | $J_2(x)$: 2 | $J_3(x)$: 3 | $J_4(x)$: 4 | $J_5(x)$: 5 |
| $s$ = 1 | 2.4048 | 3.8317 | 5.1356 | 6.3802 | 7.5883 | 8.7715 |
| 2 | 5.5201 | 7.0156 | 8.4172 | 9.7610 | 11.0647 | 12.3386 |
| 3 | 8.6537 | 10.1735 | 11.6198 | 13.0152 | 14.3725 | 15.7002 |
여기서 $\nu \ne 0$인 경우는 자명해인 $j_{\nu, 0}$ = $0$이 존재한다. 위 표보다 더 정확한 영점을 구하고 싶으면
울프럼 알파(Wolfram Alpha)가 제공하는 BesselJZero$[\nu, s]$ 함수를 쓰면 된다.
[표 10.2] 제1종 베셀 함수 미분의 영점 특정값: $J_\nu' (j_{\nu, s}')$ = $0$
| $j_{\nu, s}'$ | $J_0'(x)$: $\nu$ = 0 | $J_1'(x)$: 1 | $J_2'(x)$: 2 | $J_3'(x)$: 3 | $J_4'(x)$: 4 | $J_5'(x)$: 5 |
|---|
| $s$ = 1 | 3.8317 | 1.8412 | 3.0542 | 4.2012 | 5.3175 | 6.4156 |
| 2 | 7.0156 | 5.3314 | 6.7061 | 8.0152 | 9.2824 | 10.5199 |
| 3 | 10.1735 | 8.5363 | 9.9695 | 11.3459 | 12.6819 | 13.9872 |
여기서 $J_0'(0)$ = $0$이라서 위 표에 자명해(trivial solution)인 $j_{0, 0}'$ = $0$을 추가한다. 식 (5.6)에 의해 $J_0'(x)$ = $-J_1(x)$이므로, 항상 $j_{0,s}'$ = $j_{1,s}$를 만족한다.
[영점 공식: $Z_\nu(x)$와 $Z_\nu'(x)$]
 (10.1)
(10.1)
[증명]식 (5.8)을 변형해서 식 (10.1)의 좌변처럼 만든다.
______________________________
제2종 베셀 함수는 $x$ = $0$에서 발산하지만, 식 (10.1)의 좌변 조건에서는 $x$ = $0$도 근이 될 수 있다.
 (1)
(1) (2)
(2) (3)
(3)

 (4)
(4) (5)
(5) (6)
(6) (7)
(7)

 (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12)
 (13)
(13) (14)
(14) (15)
(15) (16)
(16) (17)
(17) (18)
(18) (19)
(19) (20)
(20) (21)
(21) (22a)
(22a) (22b)
(22b) (23)
(23) (24)
(24) (25)
(25) (1)
(1) (3)
(3) (4)
(4)
 (6)
(6)

 (8)
(8)
 (9)
(9) (10)
(10) (11)
(11)
 (1)
(1) (2b)
(2b)

 (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6)

 (1.9)
(1.9) (1.10a)
(1.10a) (1.10b)
(1.10b) (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13)
 (1.15)
(1.15) (1.16)
(1.16) (1.17)
(1.17) (1.18)
(1.18)
 (1.20)
(1.20)
 (1.22)
(1.22)

 (1.25)
(1.25) (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5)
 (2.6)
(2.6) (2.7:
(2.7:  (2.8)
(2.8)
 (2.9a)
(2.9a) (2.9b)
(2.9b) (2.9c)
(2.9c) (2.10)
(2.10) (2.11)
(2.11) (2.12)
(2.12) (2.13)
(2.13)
 (2.14)
(2.14)


 (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19)
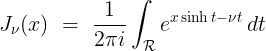 (2.20)
(2.20)


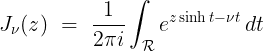


 (3.1a)
(3.1a) (3.1b)
(3.1b) (3.2)
(3.2) (3.3)
(3.3)

 (3.6)
(3.6) (3.7)
(3.7) (3.8)
(3.8) (4.1)
(4.1) (4.2a)
(4.2a) (4.2b)
(4.2b) (4.3a)
(4.3a) (4.3b)
(4.3b) (4.4)
(4.4)
 (4.6)
(4.6)
 (4.8a)
(4.8a) (4.8b)
(4.8b) (5.2)
(5.2) (5.3)
(5.3) (5.4)
(5.4) (5.5)
(5.5) (5.6)
(5.6) (5.7)
(5.7) (5.8)
(5.8) (5.9)
(5.9) (6.1)
(6.1) (6.2)
(6.2) (6.3)
(6.3) (6.4)
(6.4) (7.1)
(7.1) (7.2)
(7.2) (7.3)
(7.3)
 (7.5)
(7.5)
 (8.1)
(8.1) (8.2)
(8.2) (8.3)
(8.3) (8.4a)
(8.4a) (8.4b)
(8.4b)

 (8.6b)
(8.6b)
 (8.8a)
(8.8a) (8.8b)
(8.8b) (8.9)
(8.9)
 (9.1)
(9.1) (9.2)
(9.2)

 (10.1)
(10.1)