1. 텐서
2. 행렬
3. 행렬식
벡터(vector) 혹은 행렬(matrix)과 분명히 구별되는 텐서(tensor)의 특성은 좌표 불변(座標獨立, coordinate independent or coordinate invariant)이다. 텐서의 좌표 불변성을 좌표 변환(座標變換, coordinate transform) 관점으로 생각해본다. 최초의 좌표계(座標系, coordinate system)이자 우리 직관과도 잘 일치하는 좌표계는 [그림 1]의 데카르트 좌표계(Cartesian coordinate system)이다.

[그림 1] 2차원과 3차원 데카르트 좌표계(출처: wikipedia.org)
[그림 2] 1차원 데카르트 좌표계의 계량 혹은 측도 표현(출처: wikipedia.org)
계량은 길이를 재는 단위(unit interval)이다. 예를 들어, [그림 2]는 1이라는 계량으로 무한히 좌우로 연결하면 1차원 데카르트 좌표계 $(x)$가 됨을 보여준다. 가로 방향에 수직 방향인 세로 방향으로 좌표축을 확장하면 [그림 1]의 왼쪽에 있는 2차원 데카르트 좌표계 $(x, y)$를 생성할 수 있다. 마찬가지로 [그림 1]의 오른쪽처럼 높이 방향으로 확장하면 3차원 데카르트 좌표계 $(x, y, z)$가 얻어진다. 우리가 쉽게 상상할 수 있는 데카르트 좌표계를 좌표 변환의 기준 좌표계라고 보통 생각한다.

[그림 3] 근방의 개념(출처: wikipedia.org)
좌표계의 차원은 3차원이라 가정해도 큰 문제가 없으므로[∵ 차원 확장은 좌표점을 구성하는 좌표의 수를 늘리면 쉽게 되므로] 데카르트 좌표계 $X$ = $(x^1, x^2, x^3)$에서 일반 좌표계(generalized coordinate system or curvilinear coordinate system) $U$ = $(u^1, u^2, u^3)$로 가는 일반적인 좌표 변환을 아래로 정의한다.
 (1)
(1)
텐서에서 말하는 좌표 변환은 기저 벡터(basis vector)의 변경이라 생각하면 쉽다. 예를 들어 벡터(vector) $\bar A$는 데카르트 좌표계에서는 $\bar A(x,y,z)$ = $A_x(x,y,z) \hat x + A_y(x, y, z) \hat y + A_z(x, y, z) \hat z$로 표시할 수 있다. 하지만 좌표 변환한 원통 좌표계(circular cylindrical coordinate system)에서는 동일한 벡터를 $\bar A(\rho, \phi, z)$ = $A_\rho (\rho, \phi, z) \hat \rho + A_\phi (\rho, \phi, z) \hat \phi + A_z (\rho, \phi, z) \hat z$로 표현한다. 비슷하게 구 좌표계(spherical coordinate system)에서는 $\bar A(r, \theta, \phi)$ = $A_r (r, \theta, \phi) \hat \rho + A_\theta (r, \theta, \phi) \hat \theta + A_\phi (r, \theta, \phi) \hat \phi$처럼 쓸 수 있다. 또한 위치 벡터(position vector)는 텐서를 구성 못할 수도 있으므로,[∵ 좌표계의 원점이 다르면 위치 벡터는 서로 달라진다.] 식 (1)에 있는 위치 벡터의 차이를 텐서로 정의해야 함에 주의한다. 위치 벡터의 차이를 한없이 줄여가면 좌표계의 미분(differential)을 아래처럼 정의할 수 있다.
 (2)
(2)
여기서 $i$는 자유 첨자(free index: 합 기호에서 한 번만 출현하여 텐서가 표현하는 방정식을 명확히 표시), $j$는 무효 첨자(dummy index: 합 기호에서 두 번 출현하여 합 기호가 생략됨을 표시, 자유 첨자와 같지 않으면 다른 문자로 변경 가능), 동일한 지표(指標, index: 식 (2)에서 $j$)가 반복되어 합산 기호(summation symbol) $\Sigma$를 생략하면 아인슈타인 표기법(Einstein notation)이라 한다. 즉, 곱해진 기호에서 동일한 지표가 출현하면 합 기호 $\Sigma$가 있다고 생각해야 한다. 텐서 이론에서는 아인슈타인 표기법을 거의 사용하기 때문에 식 (2)에 익숙해져야 한다. 식 (2)의 미분 개념이 유용한 이유는 [그림 3]의 근방(近方, neighborhood) 관점으로 생각할 수 있다. 미분은 한없이 작아지는 두 지점을 의미하기 때문에 특정한 점 $P$의 3차원에 대한 미분을 [그림 3]에 있는 근방이라 생각할 수 있다. 이 근방을 모두 합치면 3차원 공간을 모두 만들 수 있다. 즉, 좌표계간의 일반적인 좌표 변환을 식 (2)를 이용해 표현할 수 있다. 그러나 식 (2)가 성립하기 위해서는 아래 관계식이 반드시 성립해야 한다.
 (3)
(3)
식 (3)에 나오는 결과는 유명한 야코비 행렬식(Jacobian determinant or Jacobian)이다. 여기서 야코비 행렬식은 야코비 행렬(Jacobian matrix) $\bf J$의 행렬식[= $|{\bf J}|$]이다. 예를 들어 2차원인 경우 야코비 행렬 $\bf J$는 식 (4)로 표현할 수 있다.
 (4)
(4)
여기서 $\bf J$는 $(x, y)$에서 $(x', y')$로 가는 좌표 변환에 사용한다. 이는 식 (4)의 야코비 행렬을 만들 때 좌표 성분 $x' = x'(x, y)$와 $y' = y'(x, y)$를 $x$와 $y$에 대해 편미분하기 때문이다. 식 (2)에 있는 데카르트 좌표계 $X$의 미분[혹은 근방] $dx$와 일반 좌표계 $U$의 미분[혹은 근방] $du$가 식 (1)의 좌표 변환을 통해 상호 연결되기 위해서는 식 (3)의 야코비 행렬식이 0이 아니어야 한다. 행렬식이 0이 아니면 식 (4)의 역행렬(inverse matrix)이 존재해서 $dx$와 $du$가 식 (4)의 행렬 관계를 통해 서로 종속적이 되도록 변환할 수 있다. 즉, 식 (4)를 통해 $dx$는 $du$를 만들 수 있고 식 (4)에 있는 야코비 행렬의 역행렬을 만들어 $du$가 $dx$를 생성하도록 할 수 있다. 이를 정리하면 아래와 같다.
일반 좌표계간의 좌표 변환이 일대일 대응(一對一對應, one-to-one mapping)이 되기 위해서는 좌표 변환의 야코비 행렬식이 0이 아니어야 한다.

[그림 4] 공변 벡터와 반변 벡터(출처: wikipedia.org)
또한, 좌표계가 만들어지기 위해서는 좌표계를 구성하는 벡터(vector)가 정의되어야 한다. 텐서 이론에서는 두 가지 종류의 기저 벡터(basis vector)를 [그림 4]와 같이 정의한다.
 (5: 공변 기저 벡터)
(5: 공변 기저 벡터) (6: 반변 기저 벡터)
(6: 반변 기저 벡터)
식 (5)에 있는 일반 좌표계 $U$의 위치 벡터는 아래로 정의한다.
 (7)
(7)
여기서 $O$는 데카르트 좌표계 $X$의 원점이며 좌표 변환이 정해지면 고정된다.[미분 관점에서 좌표점 $O$는 고정되었기 때문에 없는 것과 마찬가지이다.] 또한, 일반 좌표계 $U$에서는 위치 벡터지만 데카르트 좌표계 $X$에서는 위치 벡터의 차이로 정의함을 눈여겨 봐야한다. 텐서가 되려면 좌표 불변성을 만족해야 하기 때문에 식 (7) 정의를 따라야 한다. 식 (5)는 좌표축의 기저 벡터(basis vector)를 정의할 때 사용하는 일반적인 방법이다. 예를 들어 데카르트 좌표계의 기저 벡터는 아래식으로 얻을 수 있다.
 (8)
(8)
식 (5)를 수식적으로만 보면 위치 벡터 $\bar r$을 $u^i$ 방향으로 편미분하라는 의미이다. 그러면 $u^i$가 변하는 방향을 나타내는 벡터가 얻어진다. 즉, $u^i$축을 표현하는 벡터가 된다. 식 (6)은 변환 $u^i$에 대한 구배(gradient)이다. 구배 연산자는 정상[꼭대기] 검출기이기 때문에 $u^i$가 최대로 변하는 방향을 얻을 수 있다. 데카르트 좌표계에서는 식 (5)와 (6)의 벡터는 서로 동일하다.[$u^1 = x$, $u^2 = y$, $u^3 = z$라 가정해서 식 (6)에 대입해보라.] 하지만 일반 좌표계인 경우는 같을 필요가 없다. 식 (5)와 (6)에 제시한 벡터의 관계식을 얻기 위해 내적(inner product)을 취한다.
 (9)
(9) and
and  (10)
(10)
신기하게도 벡터 내적(dot product)인 식 (9)는 식 (10)으로 표현되는 크로네커 델타(Kronecker delta)가 된다. 식 (9)에서 $u^i$의 편미분이 크로네커 델타가 되는 이유는 무엇일까? 바로 편미분의 정의 때문이다. 편미분에서는 내가 관심있는 변수[식 (9)에서 $u^j$]가 아니면 모두 상수로 취급하므로 $i \ne j$인 경우는 상수 취급되어 모두 0이 된다.
좀더 엄밀하게 식 (5)와 (6)의 벡터를 표현하면, 식 (5)는 공변 벡터(共變, covariant vector or covector), 식 (6)은 반변 벡터(反變, contravariant vector: 흔히 벡터라고 함)라고 한다. 공변 벡터는 다른 말로 미분 형식(differential form) 혹은 1차 형식(one-form: 단순하게 생각하면 텐서 생성시 벡터를 하나만 사용한 형식이며, 1차 형식의 원래 정의는 벡터에서 좌표 성분을 뽑는 함수 관계이다.)[1]이라 한다. 식 (5)와 (6)처럼 텐서에서는 공변과 반변을 나타내기 위해 아래첨자(subscript, lower index)와 위첨자(superscript, upper index)를 사용한다. 수학적으로만 보면 $\partial x^j / \partial u^i$로 표현되면 공변 특성, $\partial u^j / \partial x^i$라면 반변 특성이 된다. 즉, 식 (5)에 있는 $\partial x^j / \partial u^i$는 데카르트 좌표계 $X$가 있고, 이 성분을 일반 좌표계 $U$의 성분 방향으로 미분한다는 뜻이다. 이는 $X$에서 $U$로 가는 좌표 변환 특성을 표현하고 있으므로 공변[좌표 변환과 비례]이 된다. 반면 반변[좌표 변환과 반비례]은 $\partial u^j / \partial x^i$가 되어, 공변과는 거꾸로 $U$ 성분을 $X$ 성분 방향으로 미분하는 특성을 표현한다. 미분 연산자 관점으로 보면 식 (5)와 (6)이 공변과 반변을 표현하는 의미를 더 쉽게 생각할 수 있다. 공변 미분 연산자는 $\partial x^j / \partial u^i \cdot \partial / \partial x^j = \partial / \partial u^i$처럼 변환된다.[분명 미분 연산자는 $X$에서 $U$로 갔다.] 반변은 $\partial u^j / \partial x^i \cdot \partial / \partial u^j = \partial / \partial x^i$이다.[반변은 $U$에서 $X$로 갔다.] 좌표 변환[$X \to U$]에 대해 함께 변하는 공변과 거꾸로 변하는 반변 특성이 미분 연산자 변환에서 잘 나타난다. 예를 들어 $u^i = 2 x^i$인 좌표 변환에서, $\bar a_i$는 $X$의 위치 벡터를 $U$ 성분으로 미분해 공변 특성인 $1/2 \cdot \hat x_i$가 된다. 반변은 공변과 반대되므로, $\bar a^i = 2 \hat x_i$가 얻어진다. 이 결과를 벡터 성분 관점에서 본다. $X$ 좌표계에서 $A \hat x_i$인 벡터는 공변과 반변 기저 벡터 관점에서 $A \hat x_i$ = $(2A) (1/2 \cdot \hat x_i)$ = $(1/2 \cdot A) (2 \hat x_i)$로 각각 표현된다. 즉 좌표 변환[$X \to U$]에 대해 함께 변하는 공변과 거꾸로 변하는 반변 특성을 벡터 성분에서 관찰할 수 있다.
공변[위치 벡터의 $u^i$ 편미분 방향]과 반변[등치면(isosurface) $u^i$의 최대 변화 방향] 벡터 관계는 어떤 좌표축의 접선과 수직 성분 관계가 아니다. 예를 들면 반변 벡터는 데카르트 좌표에서 $\hat x$로 정하고, 공변 벡터는 $\hat x$에 수직인 $\hat y$ 혹은 $\hat z$ 중 하나로 정하지는 않는다. 물론 이렇게 될 수도 있지만 일반론을 말한다. 오히려 공변과 반변 벡터는 반드시 좌표 변환 관점에서 생각해야 한다. 단순히 서로 접선과 수직 관계로 공변과 반변 벡터를 정의하면 데카르트 좌표계에서 공변과 반변 벡터가 동일한 이유가 설명되지 않는다. 예를 들어 식 (5)와 (6)에서 $u^1 = x^1$라 두면 $\bar a_1$ = $\bar a^1$ = $\hat x$가 되어 공변과 반변이 특정 좌표축에 접선과 수직이 아님을 알 수 있다.[∵ 동일한 방향이므로 특정 좌표축에 접함과 수직이 동시에 될 수 없다.] 그래서 공변과 반변은 단어 의미 그대로 미분 연산자나 기저 벡터의 변환이 좌표 변환과 정비례로 변하는지 혹은 반비례로 변하는지를 의미한다.
여기까지 이해했다면 이 부분도 생각한다. 텐서에서는 왜 이렇게 복잡하게 벡터를 정의하는가? 바로 동일한 물리적 현상을 다른 좌표계에서 보기 위해서이다.[텐서는 임의의 기하 구조를 좌표 독립적으로 표현하기 위한 표기법임을 기억한다.] 좌표 변환을 한다면 그 특성은 비례 혹은 반비례 특성을 가진다. 여기에 벡터적 특성을 도입하여 공변[좌표 변환과 비례]과 반변[좌표 변환과 반비례]으로 표현한다. 물론, 식 (9)의 증명처럼 공변과 반변 벡터는 기하학적으로 서로 수직인 중요한 성질도 있다. 또한 공변 벡터와 반변 벡터의 중요한 특징은 좌표 변환의 일대일 대응 조건인 식 (3)에 있다. 야코비 행렬식이 0이 아니기 때문에 공변 벡터는 서로 독립이다. 마찬가지로 반변 벡터도 서로 독립이다. 이를 이해하려면 식 (3)에 있는 야코비 행렬을 식 (11)과 같이 반변 벡터와 공변 벡터로 표현하면 된다.
 (11)
(11)
식 (11)로 표현된 야코비 행렬의 행렬식이 식 (3)에 의해 0이 아니기 때문에 당연히 서로 독립이다. 즉, 좌표계를 표현하는 기저 벡터로 사용할 수 있다. 또한, 식 (9)와 식 (11)을 연결하면 식 (11)에 있는 야코비 행렬은 서로 역행렬 관계임을 쉽게 알 수 있다.
 (12)
(12)
즉 일반화된 좌표계에서는 기저 벡터가 서로 수직이 아니므로 사용하기가 무척 불편하다. 하지만 이를 공변 벡터와 반변 벡터로 표현하면, 식 (12)나 식 (15)에 의해 공변 벡터와 반변 벡터는 서로 수직이므로 직교성(orthogonality)을 이용해서 좀더 편하게 일반화된 좌표계를 다룰 수 있다.
식 (5)와 완전 미분(exact differential)을 이용해 위치 벡터의 미분 $d \bar r$을 공변 벡터 관점에서 정의한다.
 (13)
(13)
식 (13)에서 $du^i$는 공변 벡터를 위한 미분소이지만 반변으로 표현했다. 왜냐하면 식 (9)에 의해 반변 벡터를 식 (13)과 내적하면 반변 성분인 반변 미분소가 얻어지기 때문이다. 식 (13)과 비슷한 방식으로 동일한 위치 벡터의 미분 $d \bar r$을 반변 벡터 관점에서 정의할 수 있다. 또한 식 (13) 이전까지는 위치 벡터 정의를 위해 반변 좌표 성분인 $u^i$를 사용했지만, 식 (13)의 쌍대(duality)를 얻기 위해 공변 좌표 성분 $u_i$의 도입이 필요하다. 이를 종합하여 위치 벡터의 미분 $d \bar r$을 새롭게 정의하면 다음과 같다.
 (14)
(14)
여기서 $du_i$는 공변 성분을 표현하는 공변 미분소이다. 식 (13)과 (14)는 각각 공변 및 반변 벡터 표현식(covariant and contravariant vector representations)으로 간주할 수 있다. 식 (14)에 나온 공변 미분소 $du_i$를 계산하기 위해 아래 관계식을 고려한다.
 (15)
(15)
여기서 $g^{ij}, g_{ij}$는 계량 텐서(metric tensor)이다. 식 (15)의 첫째 식을 보면 어떤 반변 기저 $\bar a^i$는 다른 공변 기저 $\bar a_j$에 항상 수직이다. 예를 들면 $\bar a^1$은 $\bar a_2$와 $\bar a_3$에 수직이다. 평면 방정식 관점으로 보면, 기저 벡터 $\bar a_2$와 $\bar a_3$가 만드는 평면은 항상 $\bar a^1$에 수직이다. 마찬가지로 $\bar a_1$은 $\bar a^2$와 $\bar a^3$에 수직이며, 기저 벡터 $\bar a^2$와 $\bar a^3$로 표현한 평면은 $\bar a_1$에도 수직이다. 계량 텐서를 이용하면 공변과 반변 미분소를 식 (15)처럼 서로 변환할 수 있다. 식 (5), (6), (15)를 이용해 계량 텐서를 구하면 아래와 같다.
 (16a)
(16a) (16b)
(16b)
식 (16)이 거리를 측정할 수 있는 계량 텐서인 이유는 선미분소 $ds$를 아래와 같이 계산해보면 분명히 알 수 있다.
 (17)
(17)
[그림 5] 데카르트 좌표계의 거리(출처: wikipedia.org)
데카르트 좌표계 $X$에서 일반 좌표계 $U$로 가는 좌표 변환 중 $U$가 데카르트 좌표계인 경우의 계량 텐서는 식 (16)에 의해 크로네커 델타가 된다. 그러면 선미분소는 [그림 5]처럼 우리가 잘 아는 피타고라스의 정리(Pythagorean theorem)를 만족하게 된다.
 (18)
(18)
계량 텐서의 성질은 식 (17)을 바탕으로 아래와 같이 증명할 수 있다.
 (19)
(19) (20)
(20)
이상의 논의를 바탕으로 임의의 좌표계에서 표현된 텐서가 좌표 불변성을 갖는지 증명한다. 벡터 $\bar A$는 일반 좌표계 $U$에서 정의되고 벡터 $\bar B$는 일반 좌표계 $V$에서 정의된다고 가정한다. 식 (2)와 (5)를 이용하여 식 (13) 형태의 공변 벡터 표현식으로 벡터 $\bar A, \bar B$를 표현하면 다음과 같다.
 (21)
(21)
식 (21)에 완전 미분의 특성을 적용하면 벡터 $\bar A, \bar B$가 등가임을 보일 수 있다.
 (22)
(22)
식 (22)가 성립하기 때문에 텐서 개념을 좀더 확장할 수 있다. 지금까지 논의에서 좌표 변환의 출발점은 데카르트 좌표계 $X$로 한정했지만, 더 일반화해서 임의의 일반 좌표계 $U$에서 $V$로 가는 좌표 변환을 텐서 관점으로 고려할 수 있다. 식 (9)에 있는 반변 벡터와 공변 벡터의 관계식도 일반화할 수 있다.
 (23)
(23)
즉 일반 좌표계 $U$에서 식 (9)가 성립하면, 식 (23)에 의해 일반 좌표계 $V$에서도 식 (9)와 같은 관계가 자동적으로 얻어진다.
그러면 벡터와 유사한 1차 텐서(1st order tensor)를 일반화하여 혼합 텐서(mixed tensor)를 정의한다. 1차 텐서를 표현한 식 (5)와 (6)과 유사하게 고차 텐서를 정의하면 다음과 같다.
 (24)
(24)
식 (24)가 복잡해 보이는가? 어렵게 생각할 필요없다. 식 (5)와 (6)처럼 표현되면 텐서량이 되기 때문에 고차 텐서도 식 (24)처럼 표현되어야 한다고 생각하라. 혼합 텐서는 공변 텐서(covariant tensor)와 반변 텐서(contravariant tensor)의 곱이기 때문에 식 (24)를 아래식으로 분해해서 표현할 수 있다.
 (25)
(25)
여기서 $U, X$는 반변 텐서이며 $V, Y$는 공변 텐서이다. 식 (24)와 (25)를 이용해서 텐서의 연산 몇 가지를 예로 들면 아래와 같다.
 (26)
(26)
식 (26)에 제시된 대로 텐서 연산은 덧셈, 뺄셈, 곱셈만으로 구성된다. 벡터에 나눗셈이 정의되지 않는 이유, 행렬간의 나눗셈이 없는 이유[행렬 연산에서는 직접 나눗셈을 하지 않고 역행렬을 계산하여 곱셈으로 처리]와 마찬가지로 텐서는 나눗셈을 정의하지 않는다. 텐서의 나눗셈이 없더라도 식 (15)와 (20)을 이용하여 곱셈을 이용해서 나눗셈과 유사한 연산을 할 수 있다. 즉, 식 (15)에 있는 공변과 반변 개념이 필요한 이유가 나눗셈을 대체하기 위해서이다. 텐서 개념을 이용해 벡터 내적(inner product)을 다시 정의하면 아래와 같다.
 (27)
(27)
식 (27)처럼 동일한 지표를 가진 1차 공변 텐서와 반변 텐서를 서로 곱하면 0차 텐서인 스칼라가 얻어진다. 식 (27)의 과정은 축약(contraction)이라 한다. 텐서에서는 동일한 지표를 가진 공변 텐서와 반변 텐서를 곱하면 항상 텐서의 차수가 낮아지는 축약이 일어난다. 그래서, 공변 텐서와 반변 텐서는 서로 나눗셈 관계에 있다고 생각할 수 있다.[∵ 일반적으로 공변 텐서끼리 혹은 반변 텐서끼리 서로 곱하면 식 (26)처럼 텐서의 차수가 증가한다. 그래서, 텐서의 차수가 감소하면 나눗셈처럼 생각할 수 있다.]
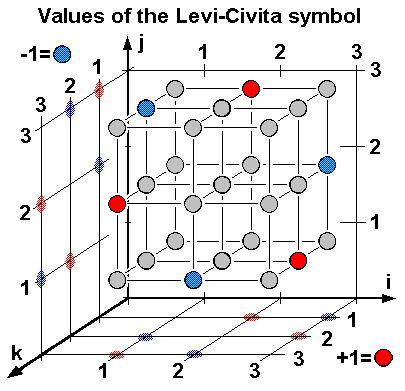
[그림 6] 3차원 레비-치비타 기호(출처: wikipedia.org)
벡터 외적(cross product)은 아래처럼 조금 복잡하다.
 (28)
(28)
식 (28)의 계산에서 공변 벡터에 대응하는 새로운 반변 벡터를 아래처럼 정의한다.
 (29)
(29)
식 (29)가 적절한 이유는 식 (15)에 있다. 예를 들어 공변 벡터 $\bar a_2$와 $\bar a_3$의 외적은 공변 벡터 $\bar a_2$와 $\bar a_3$에 수직이며 공변 벡터 $\bar a_1$과 관련된 어떤 벡터를 만든다. 또한 식 (15)에 의해 공변 벡터 $\bar a_1$과 반변 벡터 $\bar a^1$은 평행인 성분을 가지고 있고 반변 벡터 $\bar a^1$은 공변 벡터 $\bar a_2$와 $\bar a_3$에 수직이므로, 식 (29)의 정의는 완전히 타당하다. 그런데 식 (6)과 (28)에 정의한 반변 벡터는 서로 등가인가 아니면 차이가 나는가?
[공변 벡터와 반변 벡터의 유일성]
반변 벡터가 주어지면 크로네커 델타 관계를 만족하는 공변 벡터는 유일하게 정의된다. 공변 벡터가 주어진 경우에도 동일하다.
[증명]
식 (6)의 반변 벡터를 $\bar a^j$, 식 (28)의 반변 벡터를 $\bar b^j$로 정한다. 식 (23)이 성립하기 때문에 아래가 얻어진다.
 (30)
(30)
식 (30)이 성립하기 위해서는 반변 벡터 $\bar a^j, \bar b^j$가 서로 같아야 한다. 왜냐하면 모든 공변 벡터 $\bar a_i$에 대해 어떤 반변 벡터가 항상 수직일 수는 없기 때문이다.[혹은 어떤 반변 벡터든지 모든 공변 벡터의 선형합으로 표현할 수 있기 때문이다.] 즉, 모든 공변 벡터 $\bar a_i$에 대해 내적이 0인 반변 벡터는 영 벡터가 된다. 반변 벡터가 주어진 경우에도 식 (30)과 유사한 방법으로 공변 벡터가 유일함을 증명할 수 있다.
______________________________
식 (29)를 이용하면 반변 벡터에 대응하는 공변 벡터를 정의할 수 있다.
 (31)
(31)
예를 들어 공변 벡터 $\bar a_3$은 벡터 삼중적(vector triple product)을 사용해서 다음처럼 계산한다.
 (32)
(32)
식 (28)의 벡터 외적을 효과적으로 표현하기 위해 [그림 6]과 같은 레비-치비타 기호(Levi-Civita symbol) $\varepsilon_{ijk}$를 도입하였다.
 and
and  (33)
(33)
여기서 레비-치비타는 수학자 두 명의 이름이 아니다. 이탈리아 수학자인 레비-치비타Tullio Levi-Civita(1873–1941) 한 명의 이름이다. 식 (33)에 제시한 레비-치비타 기호는 행렬식(determinant) 정의에 사용한 순열(permutation) 개념과 동일하다. 즉, 행렬식의 부호함수가 짝수 순열(even permutation)이면 1을 택하고 홀수 순열(odd permutation)이면 -1을 택하는 방식처럼 $\varepsilon_{ijk}$의 순열도 식 (33)처럼 택한다. 레비-치비타 기호는 단순한 기호 같지만 공간의 기하학적 구조를 만들어주는 중요한 기호이다. 레비-치비타 기호가 포함된 식 (28)의 벡터 외적 의미를 생각해보면 이해가 된다. 예를 들어 $x$축 벡터와 $y$축 벡터를 외적하면 새로운 공간축인 $z$축 벡터가 얻어진다. 어떤 종류의 공간구조가 얻어지는지는 식 (33)이 설명해준다. 레비-치비타 기호를 활용하면 3차원을 초과하는 공간의 외적을 쉽게 정의할 수 있다. 레비-치비타 기호는 기본적으로 순열의 부호 함수(sign function)이기 때문에 아래식이 성립한다.
 (34)
(34)
아래 크로네커 델타와 관계된 항등식도 레비-치비타 기호의 재미있는 성질이다.
 (35)
(35)
식 (35)를 증명하기 위해 식 (35)에 있는 모든 지표를 변경하여 좌변과 우변이 같음을 보일 수 있지만 이미 증명된 벡터 항등식 (36)을 이용한다.
 (36)
(36)
식 (27)과 (28)을 이용해 좌변과 우변을 비교하면 식 (35)가 증명된다.
 (37)
(37)
식 (24)는 텐서의 정의이므로 어떤 양이 텐서량인가 보려면 이 양이 식 (24)처럼 표현됨을 확인하면 된다. 예를 들어 식 (16)의 계량 텐서는 아래와 같이 식 (24)에 제시한 형태이므로 2차 텐서이다.
 (38)
(38)
텐서의 좌표 불변성을 이용하여 식 (38)을 아래와 같이 유도할 수도 있다.
 (39)
(39)
텐서의 대수적 특징은 행렬(matrix)과 매우 비슷하다. 텐서는 교환 법칙(commutative law)이 성립하지 않고 결합 법칙(associative law)과 분배 법칙(distributive law)은 성립한다. 이는 행렬을 확장한 개념이 텐서라고 생각하면 쉽게 이해된다.[거듭 강조하지만 텐서는 반드시 좌표 불변성 혹은 좌표 독립성이 성립해야 한다.] 예를 들면 아래의 연산 관계가 성립한다.
 (40)
(40)
식 (40)을 더 쉽게 보려면 n애드(n-ad: $n$개의 항을 연속으로 곱함, 항이 2개인 경우 다이애드) 개념을 아래와 같이 이용하면 된다.
 (41)
(41)
텐서는 식 (40)과 같이 교환 법칙이 성립하지 않지만 식 (2)의 아인슈타인 표기법을 이용한 식 (27)과 같은 텐서 축약 계산에서는 합 기호[= $\Sigma$] 안의 숫자 위치를 바꿀 수 있다.[∵ 당연히 숫자니까 위치를 바꿀 수 있다.] 예를 들면 당연히 아래식이 성립한다.
 (42)
(42)[참고문헌]
[1] growscience, "Tensors: one-forms," Physics pages, 2011. (방문일 2011-06-25)
[다음 읽을거리]
1. 텐서 미적분학
2. 직교 좌표계 텐서 미적분학
3. 텐서를 이용한 맥스웰 방정식
식(7)에서 위치벡터를 저렇게 정의했으니까 변환해도 데카르트 좌표계 원점하고 일반좌표계 원점은 같게 되는것 같은데 맞나요?
답글삭제좌표계 정의와 관계없이 위치는 변하지 않습니다. 다만 그 위치를 나타내는 좌표값은 변할 수 있습니다.
삭제식 (7)에서도 두 좌표계에 대해 원점은 동일하지만 원점을 나타내는 좌표값은 변할 수 있습니다. 하지만 원점은 고정되어 상수이므로 미분하면 0이 됩니다.
(9)번 식에서 텐서의 계산에 의해 스칼라로 떨어져야 하므로 기저벡터가 x1,x2,x3이 1개씩이 아니라 2개씩 쓰여야 두 번째 줄의 계산으로 넘어가 지는 게 아닌지요? ^^
답글삭제식 (9)의 내적은 기저벡터 x1, x2, x3와 벡터 r에 대한 것입니다. 편미분 안에 벡터 r이 있습니다.
삭제du^i와 du_i의 표기법의 차이가 무얼나타내는지 잘 와닿지가 않는군요.
답글삭제그것에 대해 알려주시겠습니까?
도움 많이 되고 있습니다.
식 (13)과 (14)를 보세요. 동일한 미분인 dr을 공변벡터와 반변벡터로 표현할 때 얻어지는 미분소 값입니다.
삭제계속 보다가 이해가 안가서 질문했던거 였는데 답변보고 다시보고 다시보니 당연한 걸 질문한 셈이 되었네요
삭제기초지식이 부족한지 주의력이 부족한지 참... ㅜㅜ
답변 감사합니다.
별 말씀을요...
삭제안녕하세요. 질문이 있습니다.
답글삭제식 (5)의 a_i 가 covariant basis, 식 (6)의 a^i 가 contravariant basis 가 아닌지요?
즉, 임의의 점 P에서 일반좌표계의 각 좌표축에 접하는 basis 가 covariant, 좌표면에 수직인 basis가 contravariant 가 아닌지요?
본문 내용은 맞습니다.
삭제텐서는 좌표 변환 관점으로 보셔야 합니다. 단순히 접함과 수직임으로 정의하면 데카르트 좌표계에서 공변과 반변 벡터가 동일한 이유가 설명되지 않습니다. 예를 들어 식 (5)와 (6)에서 $u^1 = x$라 두면 $\bar a_1 = \bar a^1 = \hat x$가 되어 공변과 반변이 좌표축에 접함과 수직이 아님을 알 수 있습니다.
그래서 공변과 반변은 좌표 변환할 때 기저 벡터 특성이 정비례로 변하는 지 반비례로 변하는 지를 의미합니다.
예를 들어 $u^i = 2 x^i$라고 두면 $\bar a_i = 1/2 \cdot \hat x_i$, $\bar a^i = 2 \hat x_i$가 되어 정비례와 반비례 특성을 볼 수 있습니다.
전파 거북이님 복잡한 텐서를 이렇게 쉽게 설명해주시는 것도 능력입니다. 물리학 전공임에도 뒤늦게 GR에 꼽혀서 보고 있는데 큰 글이 큰 도움이 됩니다.
삭제다만, 수식으로만 이해하던 것들을 요즘 기하학적인 직관으로 이해하느라 텐서를 다시 보고 있는데 위 내용이 조금 수정되어야 할 것 같아서 글 남깁니다. 공변과 반변을 좌표에 따른 미분소 개념으로 공변, 반변으로 이해하면 좋지만 그렇게 하면 나중에 Crhistoffel 등을 계산할 때 한바닥 넘는 계산으로 풀어야 되서 기하학적인 개념이 중요한 것 같습니다.
데카르트 뿐 아니라 일반 좌표계에서도 공변기저의 경우 좌표축의 접선 방향, 반변기저의 경우 좌표축의 수직 개념이 맞습니다. 다만 반변의 경우 해당 좌표축의 수직이 아니라 정의 처럼 다른 좌표축과의 수직인 gradient 방향이지요. 즉, u_1 과 u^2, u^3 각각이 수직이어야 한다는 겁니다. 데카르트의 경우 x에 접선인 x_1과 y, z 평면에 수직인 x^1이 같지요. 일반적으로 데카르트처럼 서로 수직인 좌표는 공변, 반변이 기하학적으로 같지요. polar나 spherical을 생각해 보시면 r 이외에는 기저가 방향은 같고 길이만 다르고 곱하면 1이 되지요.
그래서 공변, 반변을 다양체에서 접선방향 tangential, 법선방향 cotangential 이라고 합니다. 예로 드신 위키의 e_1, e_2 와 e^1, e^2 를 참고하시면 기하학적인 의미도 쉽게 떠올리실꺼라 생각합니다.
(기하학적인 직관을 해야 예를 들어 spherical coordination 에서의 Christoffel을 암산으로 구할 수도 있습니다. 카르테시안에서 편미분이나 메트릭 편미분 계산을 통하지 않고서도요~^^)
핸폰으로 쓰다보니 오타가 있네요^^
삭제글 중간에,
다만 반변의 경우 해당 좌표축의 수직이 아니라 => 다만, 공변기저의 경우 ~
상상의힘님, 조언 감사합니다. 말씀하신 부분은 식 (15)의 첫째 식을 풀어서 설명하신 거죠? 본문에도 더 추가하도록 할게요. ^^
삭제넵 거북이님 식 (15)를 설명한 것이 맞습니다. 다만, 기학적으로 좌표축의 접선과 다른 좌표 평면의 수직임을 설명드린겁니다.
삭제거북이님이 말씀하신 내용,
공변과 반변 벡터는 어떤 좌표축의 접선과 수직 성분인 것은 아니다. 물론 이렇게 될 수도 있지만 일반론을 말하는 것이다. 오히려 공변과 반변 벡터는 반드시 좌표 변환 관점에서 생각해야 한다. 단순히 접선과 수직으로 공변과 반변을 정의하면 데카르트 좌표계에서 공변과 반변 벡터가 동일한 이유가 설명되지 않는다. 예를 들어 식 (5)와 (6)에서 $u^1 = x^1$라 두면 $\bar a_1 = \bar a^1 = \hat x$가 되어 공변과 반변이 특정 좌표축에 접선과 수직이 아닌 것을 알 수 있다. (∵ 동일한 방향이므로 특정 좌표축에 접함과 수직이 동시에 될 수 없다.)
요 부분이 오해를 살 수 있을 것 같습니다. 공변 기저는 좌표축의 접선이 맞고, 반변기저는 좌표축에 수직이 아니라 다른 좌표축의 gradiant 방향 (좌표 등고선 평면)의 수직으로 이해하면 데카르트에서도 공변, 반변이 기하학적으로 서로 일치합니다. 아래 위키 그림을 보면,
공변기저는 임의 좌표축에 접선 방향이고, 반변 기저는 그 좌표축 외의 다른 좌표축들이 만드는 gradiant 평면에 수직임을 알 수 있습니다. 이래야 데카르트든 임의의 좌표든 기하학적인 직관을 가질 수 있습니다.
https://en.m.wikipedia.org/wiki/Covariance_and_contravariance_of_vectors#/media/File%3AVector_1-form.svg
지속적인 조언 감사합니다, 상상의힘님. ^^
삭제잘보구 갑니다!!!!!!! 정말 고맙습니다 정말요 ㅠㅠ
답글삭제익명님도 방문 감사합니다, 정말요. ^^
삭제히히 오타 찾았어요.
답글삭제"가로 방향에 수직 방향인 세로 방향으로 좌표축을 확장하면 [그림 2]의 왼쪽에 있는 2차원 데카르트 좌표계 (x,y)를 생성할 수 있다"
[그림 2] ==> [그림1]
정말 감사합니다, 익명님. ^^
삭제반변성분은 A^i , a_i 요것은 반변기저 인가요?
답글삭제예, 맞습니다.
삭제식(1)에 나오는 x^1, x^2, x^3 은 x_1, x_2, x_3이랑 다른가요? 지금까지 제가 좌표축을 후자로 사용했는데 여기서 갑자기 위에 있으니 당황스러워서요 ㅜㅜ 이것도 공변, 반변과 관련이 있는 건가요?
답글삭제예, 맞습니다. 식 (13)과 (14)를 잘 보세요.
삭제데카르트 좌표계에서는 공변과 반변이 서로 같기 때문에 편한 대로 쓰시면 됩니다. 하지만, 일반 좌표계에서는 정확히 구분하셔야 합니다.
그렇군요! 그럼 기초적인 질문이지만 한가지만 더 질문하겠습니다.
삭제그럼 식(1)에서 u 가 공변으로 잡힌 이유는 무엇인가요? ㅜㅜ 기초적인 것 같은데, 아무리 봐도 그 부분이 자꾸 모르겠습니다.
그건 선택의 문제입니다. 일관되게만 잡으면 됩니다.
삭제기초적인 질문임에도 답변해주셔서 감사합니다!
삭제식 (13)은 아인슈타인 표기가 쓰인건가요? 완전미분 (즉 함수의 미분소?)은 앞에 시그마가 있는 걸로 알고 있어서요. 혹시 함수랑 벡터는 다른 건가 해서 질문 드려봅니다.
답글삭제맞습니다. 아인슈타인 표기법입니다.
답글삭제벡터와 함수는 다릅니다. 예를 들면 벡터중에도 벡터 상수와 벡터 함수가 있습니다.
감사합니다!! 요새 이 블로그에 빠져서 연구도 안하고 수업도 안들어요...이러면 안되는데ㅠㅜㅠ
답글삭제중학교시절 수학시간과 대학교 선대 시간에서 자주 다루던 점의 이동과 좌표계의 이동을 종합적으로 다뤄주는게 텐서라는 거네요. 좌표계의 이동은 vector(반변 기저 벡터), 점의 이동은 covector(공변 기저 벡터)로 표현하는거 같네요.. 명확해요!! 결국 한 매트릭스의 column space는 반변 기저 벡터를 이루고, 반대로 row space는 공변 기저벡터를 다루게 되는 간단한 결론에 다다르네요. 반변 기저벡터로는 basis transition을, 공변 기저 벡터로는 transformation을.. 우와... 아 시원해라.. 정말 감사드려요ㅠㅜ
허나 하나 궁금한 점이 생겼습니다.
basis function space 간의 변환이 가능하나요? 한 예로 general한 식에서 푸리에로 가는 반변기저벡터를 알고 있다면(우리가 알고있는 dx^n = n*e^(inx)가 되겠네요), 모든 식들은 푸리에에서도 표현이 가능해 보입니다. 만약 된다면 위는 결국 우리가 알고있는 타임 스페이스(도메인)에서 주파수 스페이스로 가는 변환인가요??? 된다면 너무 신기하네요... 테일러에서 푸리에등 무한대에서 무한대로는 어려울테지만 일반 식(general space)에서 정의된 식을 테일러, 푸리에,라플라스 등등의 변환이 가능하다는 소리가 되는데..우와.....너무 신기하다....
답변 부탁드리고.. 너무 감사 드립니다.. 이렇게 수학을 하면서 쾌감을 느낀적은 전무합니다. 블로그 정독하면서 더 큰 쾌감 기대할게요!
극찬인데요, 감사합니다, 이준화님. ^^
삭제텐서라는 게 동일한 현상을 다른 좌표계에서 보는 방법을 기술하는 것이라 가능합니다.
다만 해당 좌표계에서 그 기저 함수의 완비성이 증명되어 있어야 합니다. 그러면, 완전하므로 다른 좌표계에서 얻은 결과와 동일한 결과를 얻어야 합니다.
이런 식으로 증명한 것이 바일 항등식과 좀머펠트 항등식 등입니다.
이번학기 대학원생이 되었습니다. 텐서가 무엇인지 이제야 와닿습니다 ㅎㅎㅎ 정말 감사합니다! 이글만 10번째는 읽고있는거 같은데, 읽을수록 새롭네요. 알찬 정보 감사합니다
삭제축하합니다, 이준화님. ^^ 좋은 연구 많이 하기를 바래요.
삭제전피거북이님 항상 감사합니다.ㅎㅎ
답글삭제질문하나만 할께요~
식 21번에서 벡터 A 의 성분이 나오는 과정을 잘 모르겠어서요...ㅎ그리고 반변기저벡터는 정의를 그대로 따른식같은데 맞나요?
식 (2)와 (5)를 한 번 보세요. 이 정의를 그대로 적용한 것이 식 (21)입니다.
삭제중강에 대문자 X가 어디서 나왔는지 달 모르겠어요..대문자항으로 쓰신 이유가 있으신가요?ㅎㅎ
삭제별 의미는 없고, 데카르트 좌표계를 X로 표현했습니다.
삭제아..감사합니다 ㅎㅎ
삭제저기... 왜 좌표 변환인데 편미분이쓰엿나여...??
답글삭제내가 관심있는 점 주변의 특성을 생각하기 때문입니다. 좌표 변환이라고 하는 것은 한 점이 바뀐다기 보다는 내가 생각하는 공간 전체가 바뀌는 것입니다. 그래서, 근방 개념이 필요합니다.
삭제이를 이해하려면 완전 미분을 먼저 보셔야 합니다. 아래 링크 참고하세요.
http://ghebook.blogspot.kr/2010/07/exact-differential.html
전파 거북님 저는 아직 반벽벡터와 공변벡터가 뭘의미 하는지 모르겠습니다 ㅠㅠ그담에 더욱 기초적인 저 그림 4에있는 a 하구 e에 붙어있는 위첨자와 밑첨자가 뭘의미하는지를 모르겠습니다 ㅠㅠ 도와주새욤
답글삭제원래 텐서의 시작이 반변과 공변 개념입니다. ^^ 열심히 하시길...
삭제1. 반변 벡터가 우리가 흔히 사용하는 벡터이고, 공변 벡터는 텐서에서 새롭게 정의되는 개념입니다.
좌표계를 정의하는 기저 벡터 관점에서 보면, 일반적으로 반변 기저 벡터들은 서로 수직이 아닙니다. 이 반변 기저 벡터에 항상 수직인 벡터를 정의한 것이 공변 기저 벡터입니다.
반변과 공변이란 이름을 보면, 좌표 변환을 할 때 기저 벡터의 변환 특성이 반비례이면 반변, 정비례이면 공변이라 합니다.
2. 첨자가 아래에 있는 것이 반변 벡터이고, 위에 있는 것이 공변 벡터입니다.
제가보고있는 arfken 수리물리학책과는 공변,반변 기저좌표의 정의가 반대로되어있네요..7판220p 확인한번부탁드릴게요
답글삭제박승찬님, 식 (5), (6)은 문제없습니다.
삭제아프킨 책을 다시 한 번 봐주세요. 아프킨 책도 워낙 유명해서 틀리지 않았을겁니다.
박승찬님, 지적이 맞습니다. -.- 아래 분이 다시 지적해 꼼꼼히 확인했습니다. 바로 바꿀게요. ^^
삭제와,,, 글 정말 잘읽었습니다.
답글삭제그렇다면 텐서의 수학정 정의는 어떻게 간단히 나타낼수있을까요? 꼭 식으로 정의하지 않아도 되는데 간단히 요약해서 설명해주시면 감사하겠습니다 ㅠㅠ
아래 글 참고하세요. ^^
삭제http://ghebook.blogspot.kr/2011/06/tensor.html
A와B가 텐서일때 C(=A+B)도 텐서임을 어떻게 증명하나요? 그리고 성분 Cij를 어떻게 유도하나요?
답글삭제식 (22)와 유사하게 증명하면 됩니다.
삭제1) A, B가 텐서이므로 좌표계는 편한 데카르트 좌표계로 표현할 수 있습니다.
2) A + B가 정의되려면 텐서 차수가 같아야 하므로, A, B는 같은 형태의 텐서입니다.
3) 같은 차수의 텐서를 데카르트 좌표계에서 더하는 것은 단순 연산이므로, 그 결과도 텐서여야 합니다.
글 정말 잘 읽었습니다
답글삭제3차원 tensor T의 수학적 정의가 무엇이고 성분이 9개인 이유가 뭔가요?
1. 텐서 정의는 식 (24)입니다.
삭제2. 3차원에서 정의한 2차 텐서를 묻고 있는 것이지요?
단순히 다이애드(dyad)로 생각하면 3x3 = 3^2 = 9개가 되는 것이 맞습니다.
만약 3차원에서 정의한 3차 텐서라면, 트라이애드(triad)로 생각해 3^3 = 27개가 되어야 합니다.
안녕하세요? 위에서 다른분들이 식 5, 6에 문제제기하셨는데 저도 하겠습니다. 공변과 반변의 정의가 반대로 된 것 같습니다. Arfken, Boas의 수리물리학과 이장우, 진치섭 교수님의 '벡터 및 텐서해석의 기초와 응용' 등 참고했습니다. 그리고 공변, 반변이란 이름이 붙게 된 이유로 변환전, 후 미분소의 비례관계를 말씀하셨습니다. 하지만 제가 알기론 '공변'이라는 성질은 정의한 공변 기저 벡터가 좌표변환에 의해 변환되는 것과 같이 어떤 성분이 변할 때의 성질을 말합니다. 반변은 그 반대구요. 출처로 제시한 페이지에 들어가보았지만 공변과 반변의 정의에 대한 언급은 없더군요. 말씀드린 공변, 반변의 정의와 그 의미에 대해 확인 부탁드립니다. 방정식 참고하신 출처에 대해 알려주시면 저도 한번 확인해보도록 하겠습니다.
답글삭제대형 사고(?)네요. -.- 본문 내용에 심각한 결함이 있었네요. 전체적으로 다 바꾸어야겠습니다.
삭제이런 오류를 지적해주신 Unknown님과 박승찬님께 매우 감사드려요.
바로 바꿀게요. ^^
안녕하세요. 궁금한 것이 있어서 글을 남김니다.
답글삭제a_i는 공변기저벡터이고(식 5), a^i는 반변기저벡터(식 6)이고, du^i는 공변벡터미분소, du_i는 반변벡터미분소라고 하셨는데, 식 (15)에서 공변벡터미분소를 반변기저벡터와 위치벡터 dr과 내적을 하셨는데 공변벡터미분소는 공변기저벡터와 내적해야하는 것은 아닌지해서요.
stupid한 질문은 아닐런지 염려하면서 질문을 남깁니다.
식 (9)에 의해 공변과 반변은 서로 엇갈리게 내적해야 합니다.
삭제본문이 모호할 수도 있어서 본문 내용도 약간 바꾸었습니다. ^^
아 그리고.. [그림 5] 캡션 밑의 문장에서 데카르트 좌표계 X에서 데카르트 좌표계 U라고 하셨는데.. U는 일반좌표계라고 앞에서 언급하셨는데 그 문장에서는 데카르트 좌표계의 위치벡터로 다시 명명하셨는지.. 뒷문장을 읽어보면은 일반좌표계 인것 같은데.. (제가 포스팅을 며칠에 걸쳐서 읽고 있는데 읽다보면 앞의 내용이 조금씩 포맷되서요)
삭제본문을 좀더 풀어서 썼습니다, stella님. ^^
삭제포스팅 잘 보고 있습니다. 질문이 있는데요 식 (2)로 넘어가기 전에 두 위치벡터의 차이를 텐서로 정의 해야 한다고 하셨는데요, 만약 벡터 A가 있을때 X좌표계의 출발점에 대한 위치벡터와 U좌표계의 출발점에 대한 위치벡터의 차이를 말씀하신건가요? 만약 맞다면 두 좌표계에서의 출발점에 대한 위치벡터 차이와 종착점에 대한 위치벡터 차이의 특성이 같은가요? 아무런 생각이 안드네요..ㅜㅜ
답글삭제아닙니다, 익명님. ^^
삭제동일한 좌표계의 위치 벡터 차이입니다. 이 양은 좌표 변환하더라도 그대로 유지되므로 텐서가 됩니다.
답변 정말 감사합니다. ㅎㅎ 질문 하나 더 있는데요 식 (9) (10) 바로 뒤에 이어지는 본문에서요 공변기저벡터랑 반변기저벡터크기는 항상 서로 연관이 되어 있다는 식으로 생각해도 되나요? 물론 좌표변환이 어떻게 생겨먹었는지는 구분할 필요 없다고 생각하면요...ㅜㅜ
답글삭제네, 맞습니다. 공변과 반변 벡터는 내적하면 항상 크로네커 델타가 나오기 때문에 서로 연관이 꼭 있습니다.
삭제식 (29) 뒤에 나오는 본문에서 a₂와 a₃의 외적은 a₂,a₃들과 직교하는건 알겠는데 이게 왜 a₁과 관련이 있는지 잘 모르겠습니다. 예를 들면 펼쳐져 있는 카메라 삼각대의 지지대를 각각 a₁, a₂, a₃ 으로 하는 경우의 좌표계에서는 실제로 a₂와 a₃의 외적은 a₁과 다르단 것을 쉽게 알 수 있지 않나요? 또 a₁과 a¹이 평행하다면 a₂와 a²도 평행하고 a₃와 a³도 평행한데 그러면 3개의 공변벡터와 3개의 반변벡터들 6개가 3개의 방향성만 가지나요? 이상한 질문인가요?ㅜㅜ
답글삭제1. 식 (29) 뒤에 나오는 본문을 다시 한 번 보시기 바랍니다. 가능한 한 자세하게 설명하였습니다.
삭제2. 3차원이기 때문에 기저(basis)는 3개입니다. 일반 좌표계에서는 공변과 반변의 방향이 같지 않습니다. 일반적으로 서로 다른 방향이므로 6개의 방향이 나오지만, 기저는 3개이기 때문에 독립적인 방향은 3개입니다.
반변벡터와 공변벡터에서 잘 이해가 안되는 것이 있어서 질문드립니다. 반변벡터는 공변성분과 같이 다니고 공변벡터는 반변성분과 같이 다니는 것으로 알고 있는데(그래서 항상 인덱스가 엇갈리게 오는거고) 즉 어떤 임의의 벡터 v를 반변기저벡터와 공변기저벡터로 나타내면 v = v_i e^i = v^i e_i이고 여기서 e^i, e_i는 각각 반변기저벡터와 공변기저벡터, v_i, v^i는 각각 공변성분과 반변성분인 것으로 알고 있습니다. 그런데 전파거북이님 설명대로라면 각 기저벡터의 이름(공변, 반변)이 성분이 변환하는 특징으로부터 붙은것이 되어서(즉 성분과 벡터의 인덱스 위치만 반대일뿐 공변끼리 다니고 반변끼리 다닌다는 얘기가 되는것 같아서) 제가 알고 있는것과 반대가 되어버려서 뭐가 맞는 말인지 모르겠습니다ㅜ 제가 참고한 문헌은 보아스 수리물리학이랑 벡터해석 샴 시리즈랑 영문위키입니다.
답글삭제그러니까 제가 알던 것과 글 내용에서 충돌하는 부분이 있어서 그러는데 제가 알던 내용을 정리해보면, 반변벡터는 e^1 = grad(u^1)이고 공변벡터는 e_1 = ar/au^1(a는 편미분기호 라운드로 사용했습니다)인데 이때 좌표변수 u^1=x를 k배 시켜서 ku^1(kx)이 된다고 할때 벡터 e^1과 e_1를 각각 살펴보면 (i,j,k는 직교단위벡터)
답글삭제1. e^1 = grad(u^1) = grad(x) = ax/axi+ax/ayj+ax/azk = 1*i(1)
= grad(ku^1) = grad(kx) = k*i(2)
2. e_1 = ar/au^1 = a(xi+yj+zk)/ax = axi/ax = 1*i(3)
= ar/aku^1 = a(xi+yj+zk)/akx, 여기서 kx=t라고 하면 x=t/k고
= a((t/k)i+yj+zk)/at = a(t/k)i/at = (1/k)*i(4)
인데 여기서 각 계수들을 분명히 하기 위해 *로 곱하는 표시를 했는데 1번을 보면
1*i(1) = k*i(2) = e^1이 되어 i(2)가 i(1)의 1/k배가 되어 u^i가 k배 늘어났을 때 1/k배((1/k)*i(1)=i(2))가 되었으므로 e^1, i(1), i(2)는 반변벡터고 성분(i(1)과 i(2)에 곱해진)은 1에서 k로 늘어났으므로 반변벡터는 공변성분과 함께 다니게 되는거고 2번의 경우 그 반대로 i(3)과 i(4)는 u나 x와 함께 변하는 대신 그 결합계수인 성분이 반대로 변해서 공변벡터는 반변성분과 같이 다닌다 이렇게 이해하고 알고 있었습니다.
익명님 표현이 틀리지 않았습니다.
삭제본문에 오해 소지 있는 표현은 모두 삭제하고 연산자 관점으로만 공변과 반변을 설명했습니다. 지적 감사해요. ^^
답글삭제안녕하세요, 좋은글 보고 갑니다.
기본적이고 근본적인 질문일수도 있는데요,
텐서와 공변,반변등의 목적이 "동일한 물리적 현상을 다른 좌표계에서 보기위함이다" 라고 하는데,
그렇다면, 물리적현상을 다른 좌표계로 돌려가며 보는것이 어떠한 이점이 있나요?
기계공학에서 연속체역학을 배우면서 텐서에 대해 배우고 있는데,
좌표독립성을 가지는 것이, 좌표계를 바꾸면서 현상을 해석하는것이, 왜 필요한지 궁금합니다.
예를 들어, 원기둥 해석을 할 때 데카르트 좌표계보다는 원통 좌표계를 쓰는 것이 공식화를 더 쉽게 할 수 있습니다. 어떤 좌표계를 쓰든지 답은 같지만, 적용의 난이도는 다를 수 있습니다. (물론 연산이 좌표 불변성을 만족해야 하고요.)
삭제자료 감사합니다 잘보고있습니다 ^^. 본문에서 covariant와 contravariant를 설명한 부분에서 예를 든 부분이 헷갈리는데,
답글삭제[예를 들어 u_i =2x_i ui=2xi 인 좌표 변환에서, a¯i 는 X의 위치 벡터를 U 성분으로 미분해 공변 특성인 1/2⋅x^i 가 된다. 반변은 공변과 반대되므로, a¯i=2x^i 가 얻어진다.]
여기서 좌표변환 할 때 새로운 좌표인u가 기존의 x를 두배로 늘려주니까 반대로 covariant가2x^i가 되고 contravariant가 (1/2)x_i가 되어야 하는거 아닌가요 ㅠㅠ? 아직 개념이 명확히 안잡혀서 이해가 안되네요..
그리고 (식.11) 보면 왜 contravariant는 column vector으로 표현하고 covariant는 row vector로 표현하는지 궁금합니다..ㅠ
위에서 좌표 두배로 든 든 예시에서 반변 공변 a^i a_i가 베이시스벡터를 나타내는거 맞나요?? 새로운 좌표계를 왜 반변, 공변으로 두개를 표현하는지, 각각 무슨의미인지 모르겠습니다.. 텐서를 처음배우는데 완전 멘붕이네요ㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜㅜ
삭제1. 공변과 반변은 좌표 변환 관점에서 봐야 합니다. 까딱하면 헷갈려요. (저도 헷갈려 본문을 거꾸로 서술하는 사고를 친 적도 있어요. ^^) 본문에 내용을 좀 더 추가했으니 다시 한 번 보세요.
삭제2. 공변과 반변 기저 벡터를 곱하면 항등 행렬이 나온다는 식 (12)를 표현하기 위해 행과 열 벡터로 썼습니다.
3. 임의 좌표계에서 서로 직교성을 가진 기저 벡터를 정의하는 획기적 방법이 공변과 반변이란 개념입니다. (선형 대수학에서 직교성은 매우 중요하죠. ^^)
4. 텐서는 천재들이 개척한 학문입니다. 천재들에게 찬사를 보내며 우리 같은 범인은 천천히 가야죠, 포기하지 않고...
안녕하세요 전파거북이님. 처음으로 질문 드리네요 ^.^ 혹시 식 (3)의 행렬식이 0이 아닌 이유는 R3을 표현하기 위해선 변수가 3개 필요하기 때문인가요?
답글삭제맞습니다. 3차원 공간이라서, 정상적인 좌표 변환이면 자유도가 3이라 행렬식은 0이 될 수 없습니다.
삭제전파거북이님 글을 읽다가 잘이해가 안되는 점이있습니다.
답글삭제왜 벡터를 나타낼때 공변과 반변의 곱으로 나오는건가요??
벡터A=A^ie_i 이런식으로요...
식 (9) 때문에 그렇습니다. 공변과 반변 기저 벡터는 서로 직교하고, 내적 정의에 의해 해당 성분을 뽑고 싶으면 그 성분을 표현하는 기저 벡터를 내적해야 합니다. 예를 들어 반변 성분은 $\bar A \cdot \bar a^i = A^i$처럼 연산을 해야 하므로, 식 (21)처럼 성분과 기저 벡터를 정의합니다.
삭제질문 좀 여쭙겠습니다ㅠ 몇 가지 확인하고 싶어서 글을 남겨요.
답글삭제* 식(13)의 a_i*du^i=dr은 du^i 방향으로의 증가분이고 식 (14)는 a^i*du_i=dr은 델을 취했으니 방향이 같아서 특정 du_i가 존재해서 반변의 관점으로 dr을 기술할 수 있을 것이다- 는 이해가 가는데요.
*하지만 식 (15)같은 경우 a^i*dr이 전미분이라고 했을 때 미분치가 최대가 될 때는 a^i와 dr의 방향이 같을 때인데, a^i*dr=a^i*(a^j*du_j)라고 기술할 수 있는지에 대해서 헷갈립니다.
dr=a^j*du_j의 방향은 j방향축으로 가는 증가분인건데 이게 a^i*dr과 같다고 할 수 있나요?
dr=a^j*du_j 이므로
답글삭제|dr|*r_hat=|a^j|*du_j*u_jhat 인데 두개가 동치려면 dr->0 du_j->0으로 간다고 하더라도
r_hat=u_jhat을 보여야 하지 않을까요..?
본문 내용을 약간 더 추가했습니다.
삭제기본 관점은 이렇습니다. 식 (13)은 완전 미분을 이용해 자연스럽게 나옵니다. 식 (13)의 쌍대는 어떨까요? 이걸 정의한 게 식 (14)이며, 새롭게 도입한 공변 좌표 성분을 구하기 위한 관계가 식 (15)입니다.
흠.. 쌍대가 나와서 쌍대부터 보고 있는데요, 텐서가 쌍대공간의 일반화라고 하는데 고찰을 좀 해봤거든요.
답글삭제1. 쌍대공간은 Hom(V,R)을 모아놓은 공간이고 그 기저는 Φ_i(x_j)=δ_ij를 충족하는 선형 범함수를 정의함으로 구할 수 있습니다. Hom(V,R)이므로 bijective 하니 inversion(역변환)이 존재하므로 어떤 벡터공간과 그 듀얼은 수학적 특성을 유지하는 변환이 됩니다.
2. 그런 특정 벡터집합 내 변환 후에도 변하지 않는 특성들은 물리적인 해석을할 때 유의미한 효용이 있으므로 물리학에서는 좌표계에 불변하는 물리적 특성을 텐서로 표현해냅니다.
대충 이렇게 이해해도 될까요?
너무 나가신 것 같은데요, 우왕ㅋ굳ㅋ님. ^^
답글삭제1. 위에서 쌍대라고 한 것은 공변과 반변이 서로 짝이기 때문입니다.
2. 그렇게 생각할 수 있지만, 임의로 좌표 변환해도 변하지 않는 특성을 표현하는 표기법이 텐서입니다.
1.레비치비타 식(33) 에서 두 기호의 모양 서로 다른데 두 기호가 서로곱하면 항상 1이되나요?
답글삭제2.레비치비타기호의 역텐서는 무엇인가요?
레비치비타기호는 숫자인가요?
1. 위 첨자나 아래 첨자로 적을 수 있다는 뜻입니다. 두 기호는 같기 때문에 곱하면 1이 될 수도 0이 될 수도 있습니다.
삭제2. 레비-치비타 기호는 텐서가 아닙니다. 순열을 표현하는 숫자라고 생각하면 됩니다.
그러면 포인팅벡터 s_i=입실론_ijk E_j H_k를 통해 H_k= 입실론_kij S_i E_j 로 나타 낼수 있나요?
삭제네. ^^
삭제맥스웰 방정식 자체를 텐서로 표현하려면 아래 참고하세요.
https://ghebook.blogspot.kr/2011/07/maxwells-equations-using-tensor.html
포인팅벡터 식에서 레비치비타기호는 숫자기 때문에 양변을 레비치비타 기호 나누주고 오른쪽항에서 기호가 분수로 나타나지만 1/입실론 = 입실론 으로 할 수 있다는 거죠?
답글삭제0이 되는 경우가 있기 때문에 단순히 그냥 나누면 안되고 $\pm 1$이 되는 경우만 나누어야 합니다.
삭제식(18)에 오류가 있는 것 같습니다만... 2번째와 3번째 항에 있어서 ds^2= (du^i) (du_i)가 되어야 하는 것 아닌가요? 확인 후 설명 부탁드립니다...
답글삭제식 (17)을 데카르트 좌표계에 적용한 것이라서 문제가 없습니다.
삭제식 (9)의 마지막 부분이 3배가 되어야 하는거 아닌가요?...
답글삭제식 (2)를 참고하세요. 아인슈타인 표기법입니다.
삭제base vector 가 orthonormal set 이라는 전제가 없었는데 kronecker delta로 귀결되는 이유가 뭔가요??ㅠㅠ
삭제식 (9)는 편미분과 완전 미분에 기반을 두고 있어요. 아래 참고하세요.
삭제쉽게 보면 독립 변수인 $u^i$를 자기 자신에 대해 편미분하면 1이 나오고, 다른 변수에 대해 편미분하면 0이 나옵니다.
https://ghebook.blogspot.kr/2010/07/exact-differential.html
완전 미분에 대한 개념이 잘 안잡혀 있는 상태에서 눈으로만 보고 풀으니 이런 실수를 했네요... 항상 알찬 답변 정말 감사드립니다!
삭제∂xj/∂ui⋅∂/∂xj=∂/∂ui 이게 뭔말인지 모르겠어요. ∂/∂ui에서∂/<--- 분자에 있는 이걸 어떻게 계산해요?
답글삭제익명님, 기초 미분적분학을 꼭 공부하고 텐서를 보셔야 합니다. 말씀하신 기호는 편미분 기호입니다.
삭제미분연산잔 변환이라는걸 공부해본적이 없어서 잘모르겠어요
답글삭제∂xj/∂ui⋅∂/∂xj이렇게 계산을 하면 ∂/∂ui 이렇게 계산된것 처럼 보일수도 있다는 그런 뜻인가요? 체인룰 같아보이기도 하고 기초미분적분학에 나오는 것만 보면 알수있는건지요?
답글삭제아래 완전 미분 내용을 참고하세요.
삭제https://ghebook.blogspot.com/2010/07/exact-differential.html
9번을 참고하면 될까요?
삭제좋은 정보에 늘 감사드리고 있습니다.
답글삭제질문 하나 드리고자 합니다.
본문 중에 아래와 같은 내용이 있는 데요.
-------------------------------------------------------------------------------------------------
식 (13)에서 dui는 공변 벡터를 위한 미분소이지만 반변으로 표현했다. 왜냐하면 식 (9)에 의해 반변 벡터를 식 (13)과 내적하면 반변 성분인 반변 미분소가 얻어지기 때문이다.
-------------------------------------------------------------------------------------------------
여기서, 공변 벡터를 위한 미분소이지만 반변으로 표현한 이유가 잘 이해가 안갑니다.
"반변 벡터를 식 (13)과 내적하면 반변 성분인 반변 미분소가 얻어지기 때문이다."에서
어떤 반변벡터를 식(13)과 내적한다는 이야기인지요?
수행자님, 식 (9)를 한 번 보세요. 일반화 좌표계에서는 단위 벡터가 서로 직교할 필요는 없어요. 그런데 반변과 공변 벡터는 항상 서로 수직해요.
삭제이 성질을 이용해 식 (13)을 보면 됩니다. 식 (13)에 식 (9)에 있는 반변 벡터를 곱하면 반변 벡터 방향의 내적을 구할 수 있어요.
식(9)에서 두번째에서 세번째로 갈 때 3이 곱해지진않나요?
답글삭제아 아인슈타인표기법이라면 j 가 더미인건가요?
삭제근데 아인슈타인 표기법 이어도 식 (5),(6)의 정의에서 공변 반변 벡터의 일반좌표 u^i 에서 i가 프리인덱스면 식 (9) 에서
삭제프리인덱스는 합기호를 따르는게 아니어서 i=j 라면 라운드 u^i/ 라운드 u^i 가 3개여서 3이 곱해져야 하는거 아닌가요
아 다른데서 더 보다보니 알겠네요 ^^; 원래가 아인슈타인표기법 크로네커 델타_ii 의 값이 3차원에서는 대각합이돼서 3이네요
삭제완전 미분이라서 3이 곱해지지는 않아요. 그래서 최종 결과도 크로네커 델타입니다.
삭제별건 아니지만 식 (23) 이 의미하는 바는 일반좌표계 X' 에서 일반좌표계 V 로 가는 식이므로 그 위에 문단에 두번째줄에 일반좌표계 U로 간다고 돼있는 U를 V 라고 해야하는 거 아닌가요
답글삭제그리고 식 (23) 에서 x^j 라고 쓰여진 좌표계가 데카르트랑 표현이 같지만 여기서는 일반좌표계 X' 을 말하는 건가요
1. 새로운 좌표계가 나오면 헷갈릴 수 있겠네요. 본문을 약간 고쳤어요.
삭제2. 아닙니다. 데카르트 좌표계입니다.
식 (29) 밑에 문단 마지막줄에 식(6), (28) 로 정의한 공변벡터라고 나와있는데 반변벡터 오타인가요?
답글삭제지적 정말 감사합니다, Physics님. 오타가 났네요.
삭제댓글 감사합니다. 식 (32)가 어떻게 전개된건지 혹시 알 수 있을까요
답글삭제벡터 삼중적을 적용했어요. 본문을 약간 수정했으니 다시 보세요.
삭제식 (21) 이 의미하는 바는 학부 때 배운 '벡터'는 상수와 특정방향 단위벡터의 대수적인 곱으로 표현하는데 사실 그 상수는 반변벡터고 특정방향 단위벡터는 공변벡터다 라는 뜻인가요? 식 (21) 뒤쪽에 곱해진 건 완전미분과 공변벡터 정의에 의해서 특정 벡터방향에 대한 원래 단위벡터들의 변화율의 합으로 나타내서 원하는 일반좌표계의 방향을 나타냈다는건 느낌적으로 이해가 되는데 좌측에 A^i 가 곱해지는 것 특히 대문자 X^j 가 뜻하는 바를 잘 모르겠습니다.
답글삭제데카르트 좌표계의 방향을 기준으로 편미분을 통해 어떤 특정 방향의 벡터를 나타내는 과정에 있어 어떤 값이 생기므로(공변벡터의 단위벡터에 곱해지는 것) 그 값을 상쇄하기 위해 반변벡터라는 것을 도입하기 위해 그레디언트 일반좌표계를 정의하고 곱해주는 것인가요?
편하게 계산하려고 반변과 공변 벡터를 정의합니다. 식 (12) 밑에 있는 내용을 참고하세요.
삭제훌륭한 정리입니다..
답글삭제사소한 오타^^
식 (1)아래에 설명하는 원통좌표계에서 표현하는 동일한 벡터는 rho*unit_rho + z*unit_z 로 수정바라니다.
구면 좌표계에서는 r*e_r인 것처럼... 그리고 contravariant basis vector가 미분기하에서 one-form (linear functional)과 동일한 개념인 것을 추가하면 더 좋을 듯합니다 . 감사합니다.
식 (1) 밑에 설명을 바꾸었어요. 1차 형식에 대해서는 식 (10) 밑에 간략한 설명이 있어요.
삭제14식을 13식 처럼 완전미분으로 나타내면 식이 어떻게 되는지 궁금합니다
답글삭제벡터 v가 있고 직각좌표계에서의 내적 v*v 이면 곡선좌표계에서 반변성분과 공변성분이 내적하면 v=A^i*a_i 과 v=A_i*a^i 같다는 것을 어떻게 알수있나요?? 증명...
답글삭제식 (15)를 보세요. 서로 같은 벡터가 되도록 각 성분을 맞추고 있어요.
삭제아니요...14식을 뭐라고 부르나요?? au^i/ax^i du_i,, 13식은 개념적으로 완전미분으로 와닿는데 14식은 분자의 미분소와 du과 같았서 이걸 뭐라고 부르는지 궁금해요
답글삭제특별한 이름은 모르겠는데요. 찾으면 알려주세요.
삭제저라면 식 (13)은 공변 벡터 표현식, 식 (14)는 반변 벡터 표현식 정도로 부를 것 같네요.
14식은 13식처럼 미적분의 전미분같은 개념이 없다는건가요?
답글삭제네. 식 (16)에 나오는 계량 텐서가 필요해요.
삭제고맙습니다
삭제글 너무 잘 읽고 있습니다. 좋은 글 감사합니다! 궁금한점이 있는데 식 (4)에서의 야코비행렬의 기호로 쓰신 J는 엄밀하게는 J transpose가 맞는건가요?(원래 row vector인데 column vector로 표현하고자 편의상 transpose 한 걸까요?) 그리고 식 (4)는 Jacobian matrix가 함수 f에 대한 x',y'의 미분과 x, y의 미분이 Jacobian matrix로 연결된다는 것을 의도하신건가요? 제가 제대로 이해하고 있을까요..?
답글삭제야코비 행렬은 다양하게 정의할 수 있어요. 본문에서는 편미분의 변환을 다루고 있어서 통상적인 경우에서 전치로 쓰여져 있어요. 그냥 미분소의 변환이라면, 부담없이 식 (3)과 같은 야코비 행렬로 썼을 겁니다.
삭제어쨌건 다시 보니까 처음 보는 사람이 헷갈릴 수도 있겠네요. 시간될 때 수정 해보겠습니다.
매트릭텐서는 기저가 어떻게되는지 궁금합니다.
답글삭제예를 들어 공변기저벡터2개가 있으면 매트릭텐서가 행렬로 표현하면 성분들이 (a^i)•(a^j) 이것인데 기저는 어떻개 되는지 궁금합니다
계량 텐서를 만들려 사용한 공변이나 반변 기저가 있어요.
삭제이걸 계량 텐서의 생성에 사용한 기저로 간주하면 되지 않을까요? 왜냐하면 계량 텐서는 행렬 형태라서 두 개의 기저로 만들어요.
그러면 매트릭텐서가 Σ(a^i•a^j)a^ia^j 이거 맞습니까?
답글삭제행렬을 대신해 다이애드(dyad)로 계량 텐서를 표현하고 싶은 거죠? 그렇게 쓸 수도 있을 것 같네요.
삭제감사합니다
삭제basis를 위치벡터를 해당 좌표로 편미분한것으로 정의했는데 휘어진공간에서 위치벡터가 어떻게 정의되나요? 원점을 잡으려면 차원을 하나 추가해야할텐데요..
답글삭제위치 벡터는 데카르트 좌표계와 동일하게 정의합니다. 좌표 변환해도 기하 구조는 그대로이고, 이를 구현한 수학 개념이 텐서입니다.
삭제안녕하세요 좋은 글 항상 잘 읽고 있습니다.
답글삭제다만 읽다보니 식(3)의 야코비 행렬식과 행렬 정의 너무 헷갈려서 질문 남깁니다
Arfken책 7판기준 227p의 야코비안 정의를 보면 야코비 행렬이 행 기준으로 편미분의 분자 부분이 x1 x2 x2..식으로 바뀌고 분모가 u1처럼 고정이 되어있습니다
그러나 전파거북이님 블로그나 다른 곳을 보면 반대로 서술되어 있는 곳이 많습니다
야코비안이 좌표변환을 나타낸다면 공변텐서 안의 편미분과 같은 형태가 되어야 하니 Afken 책 서술대로 가는게 맞다 싶다가도 아닌가 싶기도 하고 둘다 맞는데 제가 구분을 못하는 것 같기도 하고 헷갈립니다..
야코비 행렬은 완전 미분(exact differential)을 행렬 형태로 바꾼 겁니다. 본문에서는 이론 전개할 때, 함수를 $f$ = $u$로 두었고 독립 변수는 $x$입니다.
삭제책에 따라 함수와 독립 변수를 바꿀 수도 있어요. 이건 저자의 마음입니다.
아래 내용도 참고해보세요.
https://ghebook.blogspot.com/2010/07/exact-differential.html