[경고] 아래 글을 읽지 않고 "그라프의 덧셈 정리"를 보면 바보로 느껴질 수 있습니다.
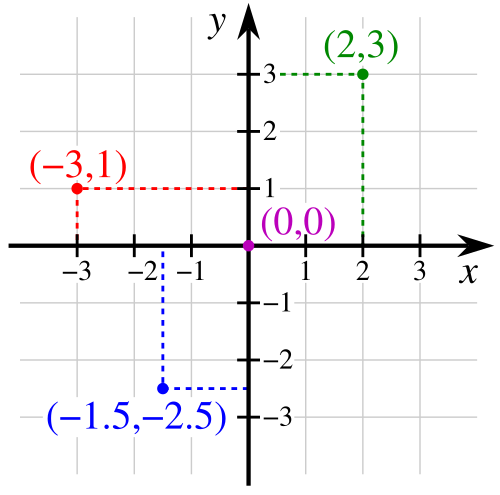
[그림 1] 데카르트 좌표계(출처: wikipedia.org)
[그림 1]의 데카르트 좌표계(Cartesian coordinate system) $(x, y)$는 좌우나 전후가 서로 대칭이라서 좌표계의 원점을 어느 곳에 설정하더라도 문제가 없다. 하지만 [그림 2]에 소개한 원통 좌표계 $(\rho, \phi)$의 원점은 유일하다. 즉, 반지름 $\rho$가 $0$이 되는 단 하나의 위치만 원점이 될 수 있다.

[그림 2] 원통 좌표계(출처: wikipedia.org)
데카르트 좌표계와 원통 좌표계가 가진 이러한 차이로 인해, 각 좌표계에 대한 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)의 해인 삼각 함수(trigonometric function)와 베셀 함수(Bessel function)의 평행 이동 특성은 하늘과 땅만큼 차이가 난다. 예를 들어, 삼각 함수를 $x_0$만큼 평행 이동할 때는 간단히 입력 변수를 $x$에서 $x - x_0$로 치환한다. 그러나 이러한 기초적인 치환 방식은 베셀 함수에서 통하지 않는다. 왜냐하면 [그림 2]에 의해 좌표계의 원점을 임의로 설정할 수 없기 때문이다. 그러면 어떻게 할까? 원통 좌표계의 성분 자체를 완전히 바꾸어서 베셀 함수의 평행 이동을 무한 급수(infinite series)로 표현하면 된다. 쉽지 않은 베셀 함수의 원점 이동을 보장하는 수학 정리가 그라프의 덧셈 정리(Graf's addition theorem)이다. 이 정리는 쉴레플리Ludwig Schläfli(1814–1895)의 제자인 수학자 그라프Johann Heinrich Graf(1852–1918)가 1893년그라프 41세, 조선 고종 시절에 증명했다.
[그라프의 덧셈 정리(Graf's addition theorem)] [1]

(1)
여기서 $-\pi \le \psi < \pi$, $J_\nu(\cdot)$는 제$\nu$차 제1종 베셀 함수(Bessel function of the first kind), $(\rho, \phi)$와 $(r, \psi)$는 서로 다른 원통 좌표계를 구성, $\nu$가 정수가 아니면 $\rho < r$인 조건이 필요, $R$과 $\Phi$는 다음처럼 정의한다.
 (2)
(2)[증명]
식 (2)의 두 식을 서로 곱해서 원통 좌표계 $(R, \Phi)$, $(\rho, \phi)$, $(r, \psi)$의 관계를 구한다.
 (3)
(3)식 (2)의 둘째식에 $e^{-i \psi}$를 곱해서 새로운 각도 관계인 $\Phi'$과 $\phi'$도 얻는다.
 (4a)
(4a) (4b)
(4b)여기서 $\Phi'$ = $\Phi-\psi$, $\phi'$ = $\phi-\psi$이다. 다음 단계로 식 (1)의 우변을 $\phi'$에 대해 쓰고 한켈 경로(Hankel contour) $\mathcal{H}$의 원점 대칭 경로 $\mathcal{C}$를 이용해 제1종 베셀 함수를 복소 적분으로 표현한다.
 (5)
(5) (6)
(6)식 (6)에 나온 무한 급수를 다시 베셀 함수의 생성 함수(generating function)로 바꾸어서 식 (3)을 대입한다.
 (7)
(7) (8)
(8)최종적으로 식 (8)의 마지막 복소 적분에서 적분 변수를 $s$ = $t e^{i \Phi'}$으로 바꾸어서 식 (1)을 증명한다.
 (8)
(8)여기서 $\mathcal{C}$와 거의 비슷한 $\mathcal{C}'$은 $s$에 대한 적분 경로이다. 차수 $\nu$가 정수는 아니라면, $k$가 커질 때 무한 급수의 항이 다음처럼 발산할 수 있다.
 (9)
(9)그래서 $\rho < r$이 성립해야 식 (1)의 무한 급수가 수렴한다.
______________________________
제2종 베셀 함수 $N_\nu(x)$에 대해서도 그라프의 덧셈 정리는 성립한다. 먼저 $N_\nu(x)$를 $J_\nu(x)$를 이용해서 정의한다.
 (10)
(10)식 (10)처럼 $J_\nu(x)$와 $J_{-\nu}(x)$를 조합해서 $N_\nu(x)$를 만들면, 식 (1)을 $N_\nu(x)$에 대한 관계로 확장할 수 있다.
 (11)
(11) (12)
(12)여기서 $k$는 정수이다. 식 (12)에 바탕을 두고 $J_{-\nu + k}(x)$에 대한 무한 급수의 합을 구한다.
 (13)
(13)여기서 $\mathcal{C}''$은 $s$에 대한 적분 경로이다. 식 (8)과 (13)을 식 (12)처럼 합쳐서 정리하면 식 (11)을 증명할 수 있다. 식 (11)을 더 일반화해서 임의의 베셀 함수 $Z_\nu(x)$[$Z$ = $J, N, H, I, K$]에 대한 덧셈 정리로 확장한다.
 (14)
(14)여기서 수렴 조건은 $\rho < r$이며, 정수 차수를 가진 $J_n(R)$은 이 조건이 필요없다. 매우 일반적인 식 (14)는 다소 복잡하므로, 식 (4b)를 이용해서 다음처럼 간략화한다.
 (15)
(15)여기서 식 (14)에 나오는 $\psi$는 각도 조건인 식 (4b)에 따라 0으로 바꾼다. 식 (15)의 두 식을 더하거나 빼서 복소 지수 함수 대신 삼각 함수의 관계로 바꿀 수도 있다.
 (16)
(16)식 (4)를 이용해 식 (15)와 (16)에 사용한 원통 좌표계 $(R, \Phi)$와 $(\rho, \phi)$의 연결 관계를 구한다.
 (17)
(17)여기서 $\phi + \alpha$ = $\pi$이다. 식 (17)은 각각 삼각형에 대한 코사인 제2 및 제1법칙(the second and first laws of cosines)을 의미한다. 따라서 원통 좌표계 $(R, \Phi)$ 및 $(\rho, \alpha)$ 혹은 $(\rho, \phi)$를 [그림 3]처럼 삼각형의 조건으로 구성한다.

[그림 3] 그라프의 덧셈 정리를 위한 삼각형 좌표계
예를 들어, 2차원 공간의 임의점 $(x, y)$에 대한 베셀 함수는 [그림 3]에 따라 원점이 $(x_0, y_0)$에 위치한 원통 좌표계 $(R, \Phi)$로 기술할 수 있다. 혹은 원점을 $(x_0', y_0')$로 바꿔서 $(\rho, \alpha)$ 혹은 $(\rho, \phi)$를 기준으로 한 베셀 함수를 만들 수도 있다. 그래서 식 (15), (16)을 원통 좌표계 $(\rho, \alpha)$ 관점으로 간단히 표현하기도 한다.
 (18)
(18) (19)
(19)여기서 무한 급수가 수렴하려면 $\rho < r$이 성립해야 한다. 예외적으로 $R$ = $0$에서 함수값이 정의되는 $Z_\nu (R)$ = $J_n(R)$인 경우, 모든 $\rho$에서 식 (18)과 (19)가 성립한다. [그림 3]의 삼각형 높이가 $0$이 되거나 점 $(x_0, y_0)$과 $(x_0', y_0')$이 만드는 직선 상에 $(x, y)$가 있으면, 식 (18) 좌변의 입력 변수는 $r, \rho$의 합이나 차가 된다.
 (20)
(20)여기서 $\Phi$ = $0$, $\alpha$ = $\pi$ 혹은 $0$이다. 만약 $Z_\nu (\cdot)$가 제1종 베셀 함수가 아니라면, $\rho < r$인 수렴 조건이 필요하다. 매우 간략화된 식 (20)은 노이만의 덧셈 정리(Neumann's addition theorem)라고 한다.

[그림 4] 그라프의 덧셈 정리를 위한 원통 좌표계
[그림 3]을 원통 좌표계 $(\rho, \phi)$에 가깝게 그리면 [그림 4]처럼 된다. 식 (3)과 유사하게 [그림 4]를 위한 원통 좌표계 $(R, \Phi)$, $(\rho, \phi)$, $(\rho', \phi')$의 관계는 다음과 같다.
 (21)
(21)여기서 $r$ = $\rho'$ = $\sqrt{x^{\prime 2} + y^{\prime 2}}$, $\psi$ = $\phi' - \pi$, $\phi'$ = $\tan^{-1} (y'/x')$, $0 \le \phi' < 2 \pi$가 된다. 식 (21)에서 얻은 원통 좌표계 관계를 식 (14)에 대입한다.
 (22a)
(22a) (22b)
(22b) (22c)
(22c)여기서 $R$ = $\sqrt{(x-x')^2 + (y-y')^2}$, $\Phi$ = $\tan^{-1} \left[(y-y')/(x-x')\right]$이다. 식 (14)처럼 식 (22)의 수렴 조건도 $\rho < \rho'$이다. 다만 $Z_\nu(R)$ = $J_n(R)$이면 이 조건이 필요없고 언제나 수렴한다. 만약 $\phi'$ = $\pi$라면, [그림 4]는 [그림 3]과 동일해진다. 이로 인해 식 (22a)는 식 (18)의 첫째식과 같아진다.
그라프의 덧셈 정리에 나오는 무한 급수의 수렴과 발산은 $Z_{\nu+k}(\rho')$의 점근적 특성이 결정한다. 차수 $k$가 매우 커서 $Z_{\nu+k}(\rho')$가 발산하는 경우에 무한 급수의 항은 다음과 같이 변한다.
 (23)
(23)여기서 $\Gamma(\cdot)$는 감마 함수(gamma function)이다. 따라서 $\rho < \rho'$인 경우에만 무한 급수가 수렴하고 나머지 범위에서는 발산한다. 또한 수렴 조건만 잘 지키면 수학 관점에서 그라프의 덧셈 정리는 언제나 잘 수렴한다. 하지만 무한 급수의 항을 더해서 수치 계산을 하는 과정은 또다른 문제를 만들 수 있다. 예를 들어, 식 (23)에 의해 $\rho \approx \rho'$ 근방에서는 무한 급수의 수렴이 매우 느리기 때문에, 무한 급수의 계산에 많은 항을 사용해야 참값에 근접하는 결과를 얻을 수 있다.
[참고문헌]
[1] J. Dereziński, "Bessel equation," University of Warsaw, Poland, 2020. (방문일 2020-12-14)
우연히 봤는데 진짜 글 꾸준히 올리신것 같습니다 거북이처럼 즐기면서 느리게 가시는 길 응원합니다
답글삭제방문 감사합니다, Unknown님. 그냥 쉬엄쉬엄 생각날 때 가끔씩 올립니다.
삭제