1. 복소수
2. 완전 미분
수학 분야에 멋지고 아름다운 이론이 많지만 수학적 아름다움의 최상은 복소 함수론(複素 函數論, complex function theory) 혹은 복소 해석학(複素 解析學, complex analysis)이다. 인간이 지금까지 제안한 이론 중에서 가장 단순하면서도 심오하고 그러면서도 너무나 아름다운 이론이 복소 함수론이다.
[그림 1] 미켈란젤로의 피에타(출처: wikipedia.org)
복소 함수론의 시작과 끝이며 가장 중요한 정리는 다음 식 (1)에 제시한 코쉬의 적분 정리(Cauchy's integral theorem) 혹은 코쉬–구르사 정리(Cauchy–Goursat theorem)이다. 이 정리는 복소 함수론을 만든 수학자 코쉬Augustin-Louis Cauchy(1789–1857)가 1814년코쉬 25세, 조선 순조 시절에 제안하고 1825년코쉬 36세, 조선 순조 시절에 명확히 증명했다[2]. 그러면 복소 함수론의 아름다움을 느낄 수 있는 다음 적분을 꼼꼼히 보자.
 (1)
(1)
여기서 닫힌 경로 $c$는 단순 연결(simply connected) 경로이며, $f(z)$는 닫힌 경로 $c$가 만든 내부 면적에서 항상 해석적인 함수(analytic function)이다. 단순 연결 경로는 [그림 1]처럼 경로를 줄여갔을 때 점으로 수축될 수 있는 경로이다. [그림 2]처럼 경로 내부에 구멍이 있으면 단순 연결이 아니다.
[그림 1] 구표면에 형성한 단순 연결 경로(출처: wikipedia.org)
[그림 2] 내부 구멍으로 인해 단순 연결 경로가 아닌 예(출처: wikipedia.org)

[그림 3] 복소 평면에 표시한 복소수(출처: wikipedia.org)
복소 함수론에 나오는 해석 함수(解析函數, analytic function)는 해석학(analysis)으로 분석 가능한 함수란 뜻이다. 해석학이라는 학문은 무한(infinity)과 극한(limit)을 다루는 학문이므로, 해석 함수는 우리가 생각하는 영역에서 극한이 존재하고 무한 급수(infinite series)로 표현 가능해야 한다. 따라서 실수 해석 함수(real analytic function)라면 반드시 식 (2)의 테일러 급수(Taylor series)로 표현 가능하고 수렴해야 한다.
 (2)
(2)
실수 해석 함수와 비슷하게 복소 해석 함수(complex analytic function)는 특정한 복소 평면(complex plane)에서 테일러 급수와 같은 무한 급수가 존재해서 반드시 수렴한다.
 (3)
(3)
식 (1)에 쓰인 $f(z)$의 정확한 명칭은 복소 해석 함수이지만 간단히 해석 함수라 할 수도 있다. 식 (3)를 이용하면 식 (1)을 쉽게 증명할 수 있다. 닫힌 경로를 반지름이 $R$인 원(circle)이라 가정하면 다음이 성립한다.
 (4)
(4)
식 (4)가 $0$이 되는 이유는 분명하다. 복소 지수 함수(complex exponential function)의 의미는 [그림 4]처럼 복소 평면 상의 회전을 뜻하므로 $m > 0$인 경우는 항상 $0$이다.[∵ 복소 지수 함수에 대한 경로 $c$의 시작점과 끝점이 같기 때문에 적분하면 당연히 $0$이 된다. 혹은 식 (4)의 적분 자체가 회전을 의미하므로 아무리 돌려도 제자리로 돌아오기 때문에 $0$이 된다. 한 바퀴, 두 바퀴, 혹은 아무리 많이 돌더라도 정수배로만 돈다면 항상 제자리이므로 적분값은 항상 $0$이 된다.] 여기서 가져야 하는 또 하나의 의문은 폐곡선의 내부와 외부를 어떻게 나누는가이다. 아주 일반적인 경우라면 조르당 곡선 정리(Jordan curve theorem)를 이용해 폐곡선의 내부와 외부를 정의할 수 있겠지만, 우리가 고민하는 부분은 단순한 경우이므로 오른손 법칙만으로도 충분하다. 즉, 폐곡선이 휘어진 방향으로 엄지를 제외한 오른쪽 손가락을 위치시켰을 때 엄지가 위치한 부분이 폐곡선의 내부이다. 예를 들어, 오른손으로 돌려보면 [그림 1]의 폐곡선은 엄지가 구의 위쪽에 위치하므로 오른손 법칙에 의해 구의 위쪽이 폐곡선의 내부가 된다. 폐곡선이 휘지 않은 직선인 경우라면 폐곡선의 내부와 외부를 결정할 수 없다. 일반적으로 가면 더 어려워진다. 우리가 폐곡선의 내부와 외부를 판단하는 기준은 곡선이 휜 특성이다. 휘어짐은 미분과 관련되기 때문에, 미분할 수 없는 곡선[예를 들면 프랙탈 곡선(fractal curve)]이 되면 상황은 한층 더 복잡해진다.
[그림 4] 복소 지수 함수의 기하학적 의미(출처: wikipedia.org)
그런데 복소 함수를 미분하든지 적분하려면, 함수의 미분이 반드시 존재해야 한다. 복소수는 2차원 복소 평면에 존재하기 때문에, 복소수의 미분은 2차원 평면에서 정의되어야 한다. 하지만 복소 평면에서 미분할 수 있는 방법은 [그림 5]처럼 무한히 많다.

[그림 5] 복소 평면에서 미분 방법
복소 함수의 미분이 정상적으로 정의되기 위해서는 어떤 경로를 따라 미분하더라도 미분값이 같아야 한다. 이런 특성을 가진 함수는 정칙 함수(正則函數, holomorphic function)라고 한다. 복소 함수의 테일러 급수(Taylor series of complex function)에 대한 성질을 이용하면 복소수 범위에서 정칙 함수와 해석 함수는 서로 등가임을 증명할 수 있다. 예를 들어 실수축[$x$축]과 허수축[$y$축]을 따라 미분하면 다음을 얻는다.
 (5)
(5)만약 $x$축을 따라 미분한 결과와 $y$축을 따라 미분한 결과를 같다고 연립하면, 식 (5)로부터 다음 방정식을 얻을 수 있다.
 (6)
(6)
식 (6)은 복소 함수론에서 매우 중요하기 때문에 이름도 붙어있다. 바로 코쉬–리만 방정식(Cauchy–Riemann equation)이다[1]. 코쉬–리만 방정식은 리만Bernhard Riemann(1826–1866)의 박사학위 논문[1]에 처음 등장한다. 이토록 중요한 방정식을 스물다섯살 청년 리만이 제안했다는 사실이 놀랍다. 박사 학위 지도교수인 가우스Carl Friedrich Gauss(1777–1855)가 입이 닳도록 칭찬한 논문이 리만의 박사 논문이다. 성격 자체가 까칠한 가우스가 리만을 칭찬한 사실 자체가 리만의 위대성을 나타낸다. 수학 책에도 나오는 데데킨트Richard Dedekind(1831–1916)는 가우스의 마지막 제자였다. 하지만 가우스 교수는 리만 학생과 비슷한 시기에 심사를 받은 데데킨트 학생의 논문에는 별다른 평을 하지 않았다. 그만큼 수준 차이가 났다는 뜻이다.(리만과 비교되어서 그렇지, 데데킨트도 뛰어난 수학자이다.) 리만의 논문[1]에는 코쉬–리만 방정식, 가지 자름(branch cut) 방법, 등각 사상(等角寫像, conformal mapping), 리만 표면(Riemann surface) 등이 있어서 가우스의 편애를 인정해줄 만하다. 리만은 심도있게 사색해서 코쉬의 복소 함수론을 기하학(geometry)적 관점으로 새롭게 봤다. 복소 함수를 시각적으로 설명한 관점을 가우스는 특히 높게 봤다.
그러면 코쉬–리만 방정식을 통해 미분 경로에 관계없이 미분값이 동일한 정칙 함수의 성질을 증명한다. 복소 함수의 미분은 다음으로 표현가능하다.
 (7)
(7)
복소 함수는 $x, y$에 대한 이변수 함수이므로 완전 미분(exact differential)을 이용해 미분(differentiation)을 구해야 한다. 이 점을 이해하지 못하면 코쉬–리만 방정식의 의미를 알 수 없다.
 (8)
(8)
식 (6), (8)을 식 (7)에 대입해본다.
 (9)
(9)
식 (9)를 다시 식 (7)에 넣으면 복소 함수 $f(z)$의 미분을 구할 수 있다.
 (10)
(10)
식 (10)은 어떤 미분 경로를 택하더라도 미분값은 고정이므로, 코쉬–리만 방정식이 잘 성립한다. 특별한 경우를 만들어서 결과를 관찰하는 식 (10)과 같은 접근법은 수학적으로 좀 부실하다. 하지만 코쉬–리만 방정식이 성립하는 관계를 편하게 관찰할 수 있다. 리만은 편한 길을 따라가면서 엉성하게 증명하지 않았다. 실제 리만은 켤레 복소수(complex conjugate)를 이용해 식 (6)을 엄밀하게 증명했다.
 (11)
(11)여기서 $\bar z$ = $x -iy$이다. 식 (11)의 결과를 식 (7)에 넣으면 다음을 얻는다.
 (12)
(12)
미분 경로 $dz$에 관계없이 복소 함수의 미분이 일정하기 위해서는 식 (12)의 셋째 줄이 $0$이어야 한다. 우리가 어렵게 얻은 미분에 대한 조건이 바로 식 (6)의 코쉬–리만 방정식이다. 따라서 미분 경로를 어떻게 택하든지 복소 함수의 미분값이 동일한 정칙 함수는 코쉬–리만 방정식을 주어진 영역에서 항상 만족한다. 또한 코쉬–리만 방정식은 정칙 함수가 가져야 하는 성질을 함축적으로 보여준다. 정칙 함수는 실수부와 허수부가 동시에 존재하며, 각 실수부와 허수부는 모두 $x, y$의 함수여야 한다. 그래서 정칙 함수는 켤레 복소수를 포함할 수 없다. 예를 들어, $z + \bar z$ = $2x$ 혹은 $z - \bar z$ = $i2y$는 실수부나 허수부만 있어서 정칙 함수일 수 없다. 두 복소수의 합이나 차가 정칙 함수가 될 수 없는 원인은 켤레 복소수의 사용에 있다.
코쉬–리만 방정식은 복소 함수론에서 풍성한 결과를 만들어낸다. 대표적인 결과가 식 (1)의 증명이다. 코쉬의 적분 정리를 실수부와 허수부로 쓰면 다음을 얻는다.
 (13)
(13) (14)
(14)
식 (14)를 이용하면 식 (13)은 다음의 면적 적분(surface integral)으로 바뀐다.
 (15)
(15)
식 (15)가 $0$이 되려면, 복소 함수 $f(z)$는 식 (6)의 코쉬–리만 방정식을 반드시 만족해야 한다. 코쉬의 적분 정리와 코쉬–리만 방정식을 거꾸로 생각해본다. 코쉬–리만 방정식을 만족하는 정칙 함수는 식 (15)에 의해 자연스럽게 코쉬의 적분 정리를 만족한다.

[그림 6] 원형 경로의 합으로 표현한 임의의 경로
식 (4)의 원형 경로에 대한 선 적분은 $0$이 되는 결과를 이용해서 식 (1)의 코쉬 적분 정리를 더욱 직관적으로 증명할 수 있다. [그림 6]처럼 임의 경로[빨간색]를 원형 경로[녹색]의 무한 합으로 완벽히 표현할 수 있기 때문에[∵ 유한한 원형 경로로 표현하면 그림 2처럼 내부에 구멍이 생기지만 그 구멍을 다시 원형 경로로 만들면 구멍 크기를 한없이 줄일 수 있으므로] 임의 경로의 선 적분은 식 (1)처럼 $0$이 된다.
이상 소개한 코쉬–리만 방정식과 코쉬의 적분 정리를 바탕으로 복소 함수론의 다양한 정리를 증명한다. 식 (1)의 코쉬 적분 정리로부터 직접 유도가 되는 유수 정리(residue theorem)를 먼저 살펴본다. 유수 정리는 코쉬가 1831년코쉬 42세, 조선 순조 시절에 증명했다. 하지만 유수(留數, residue)라는 말은 코쉬가 이미 1826년코쉬 37세, 조선 순조 시절에 제안했었다.

[그림 7] 적분 경로 내부의 극점
[유수 정리(留數定理, residue theorem)]
 (16)
(16)
여기서 $f(z)$는 [그림 7]처럼 $z_m$에서 극점(極點, pole: 함수가 무한대로 발산하는 점)을 가지고 극점을 제외한 영역에서 해석적이며, $f(z)$의 유수 $\operatorname{Res}[f(z)]$는 $1/z$ 항의 계수이다.
[증명]
먼저 함수가 발산하는 극점은 하나라고 가정하고 $z_0$라 한다. 그러면 적분 경로를 다음처럼 변형할 수 있다.

[그림 8] 극점을 위한 적분 경로 변형
그러면 새롭게 변형된 적분 경로 내부에는 극점이 없기 때문에 $f(z)$는 영역 내부에서 해석적이다. 그래서 식 (1)의 코쉬 적분 정리를 사용할 수 있다.
 (17)
(17)
여기서 경로 $c_1, c_2$는 한없이 가까워져서 두 경로의 간격 $\Delta$는 $0$이 된다고 가정한다. 식 (17)은 극점이 있는 복소 함수를 닫힌 경로[$c$]로 적분한 값은 극점 근방 $-c_0$의 적분값과 같음을 의미한다. 또한 복소 함수 $f(z)$는 극점에서 발산하므로, 식 (3)의 무한 급수를 확장해서 $z$ = $z_0$ 근방에서는 다음처럼 표현할 수 있다.
 (18)
(18)
식 (18)은 테일러 급수와 비슷하지만 시작점이 $0$이 아닌 음의 무한대이다. 식 (18)과 같은 급수는 제안자 로랑Pierre Alphonse Laurent(1813–1854)의 이름을 따서 로랑 급수(Laurent series)라고 한다. 적분 경로 $-c_0$는 마음대로 택할 수 있으므로, 가장 쉬운 형태인 원(circle)으로 잡는다. 그러면 식 (4)를 그대로 쓸 수 있다. 사실 원을 따라 복소 지수 함수의 선 적분을 함은 복소 평면을 도는 바퀴수를 헤아림과 같다. $m \ge 0$인 경우는 반시계 방향으로 1, 2, 3, ... 바퀴씩 돌아서 제자리로 돌아오므로 선 적분이 $0$이다. $m \le -2$인 경우는 시계 방향으로 $1, 2, 3, \cdots$ 바퀴씩 돌므로 적분이 $0$이다. 특이한 경우가 $m$ = $-1$이다. 이 경우는 복소 지수 함수의 지수부가 $0$이 되므로 선 적분을 하더라도 복소 지수 함수는 변하지 않는다. 따라서, 선 적분값은 다음처럼 얻어진다.
 (19)
(19)
여기서 $\delta_{ml}$은 크로네커 델타(Kronecker delta)이며, $a_{-1}$은 선 적분하고 남은 찌꺼기 숫자라고 해서 유수(留數, residue)라 한다. 다시 말하면 유수는 복소 함수 $f(z)$의 특성이 $1/z$로 변할 때의 계수로 정의한다. 좀더 고상하게 다음처럼 표기할 수도 있다.
 (20)
(20)
극점이 한 개가 아니고 여러 개라면 식 (17)처럼 각 극점에 대해 적분 경로를 변형하면 식 (16)이 증명된다.
______________________________극점이 출현하면서 생기는 재미있는 현상은 선 적분의 경로가 반시계 방향에서 시계 방향으로 바뀌는 성질이다. 예를 들면, $z$ = $r e^{i \phi}$는 $\phi$에 대해 반시계 방향으로 회전하지만, $1/z$ = $1/r \cdot e^{-i \phi}$는 분명 시계 방향으로 돈다. 얼핏 보면 $1/z$는 $z$의 켤레 복소수 같지만 아니다. 반지름 $r$의 비율이 달라서 서로 켤레 복소수가 될 수 없다. 그리고 계산해보기 전까지는 믿기 어렵지만, $1/z$는 $z$ = $0$을 제외한 모든 점에서 코쉬–리만 방정식을 만족한다. 이로 인해 $1/z$나 그 거듭제곱 함수를 유수 정리에 포함시킬 수 있다.
[그림 9] 피카소가 그린 아비뇽의 처녀들(출처: wikipedia.org)
코쉬의 적분 정리(Cauchy's integral theorem) 혹은 유수 정리(residue theorem)를 사용할 때는 복소 영역에서 닫힌 경로를 잘 선택해야 한다. 처음에 복소 함수론을 보면 단순한 선 적분을 계산하고 있다고 느끼지만, 전혀 그렇지 않다. 복소 함수론의 재미는 우리가 마음대로 선택하는 자유로운 닫힌 경로에 있다. [그림 8]과 같은 닫힌 경로는 수학자가 그리는 아름답고 논리적인 추상화이다. 이 경로 그림은 아무렇게나 그린 듯 보이지만, 아는 만큼 보인다는 자부심으로 우리의 감성을 자극한다. 수학적으로 보면, 어떤 경로를 선택하더라도 복소 적분값은 항상 동일하게 나온다. 다만 경로 내부에 있는 함수의 정칙적(holomorphic) 혹은 해석적(analytic) 특성을 고려해서 닫힌 경로를 복소 평면에 잘 그려야 한다. 그래서 복소 함수론이라는 같은 도구를 가지고 초보자와 전문가가 쓰는 수준은 확실히 다르다. 하지만 너무 걱정하지 말자. 복소 함수론의 기본 정신만 잘 기억하면 우리도 쉽게 전문가가 된다. 즉, 선 적분을 정의하는 모든 닫힌 경로 상에서 피적분 함수는 해석적으로 잘 정의되어야 한다. 그후에 닫힌 경로 내부에 있는 극점(pole)만 찾아서 유수 정리를 쓰면 된다.
여기서 반전이 한 가지 있다. 식 (1)의 제안자는 분명히 대(大)수학자 코쉬이다. 하지만 식 (1)의 최초 발견자는 가우스Carl Friedrich Gauss(1777–1855)이다. 가우스 사후에 공개된 그의 학술 일기[3][더 자세하게는 학술 일기 19쪽, 146항목]에 식 (1)이 나온다. 코쉬 입장에서는 황당할 것이다. 이 아름다운 정리의 최초 발견자가 자신이 아니라니 큰 충격일 것이다! 떨리는 코쉬에게 위로의 말을 하자면, 가우스의 결벽증으로 인해 심한 정신적 피해를 본 수학자가 한둘이 아니다. 사원수(四元數, quaternion)를 제안한 해밀턴William Rowan Hamilton(1805–1865)도 최초 발견자가 아니며, 비유클리드 기하학(non-Euclidean geometry)의 제안자인 보이아이János Bolyai(1802–1860)와 로바체프스키Nikolai Lobachevsky(1792–1856)도 최초가 아니다. 이 모든 개념은 가우스가 먼저 생각했다. 하지만 학술 일기는 아주 개인적인 일기라서 가우스가 공개적으로 발표하지 않았다. 가우스가 죽은 후, 약 40년이 지난 1897년에 학술 일기가 발견되었다. 여기에 수학자 클라인Felix Klein(1849–1925)이 주석을 붙여 1903년클라인 54세, 대한제국 시절에 드디어 출판되었다[3]. 가우스의 학술 일기에는 정수론(number theory), 무한 급수(infinite series), 복소 함수론(complex analysis), 사원수, 비유클리드 기하학 등과 같은 당시 수학 이론을 훌쩍 뛰어넘는 다양한 내용이 들어있다. 하지만 이 모든 내용이 라틴어로 함축되어 쓰여 있고 어떤 항목은 암호처럼 기술되어 있다. 그래서 가우스의 학술 일기에는 아직까지 이해할 수 없는 부분이 조금 남아있다.
1. 기본(basics)
[비르팅어 도함수(Wirtinger derivative)]
 (1.1)
(1.1)여기서 $z$ = $x+iy$, $\bar z$ = $x-iy$이다.
[증명]
이변수 $x, y$ 대신 복소수 $z, \bar z$를 쓰는 경우는 $x$ = $(z+\bar z)/2$, $y$ = $(z-\bar z)/(2i)$로 서로 관계를 만든다. 그러면 완전 미분에 의해 실수 $x, y$에 대한 편미분을 생성할 수 있다.
 (1.2)
(1.2)______________________________
비르팅어 도함수는 코쉬–리만 방정식을 쓰지 않고 유도하기 때문에, 정칙 혹은 해석 함수 여부에 관계없이 복소수 $z, \bar z$에 대한 편미분을 정의한다. 비르팅어 도함수를 정칙 함수로 한정해 코쉬–리만 방정식을 대입하면, 매우 재미있는 아래 관계도 증명할 수 있다.
 (1.3a)
(1.3a) (1.3b)
(1.3b)여기서 $f$ = $u +i v$이다. 따라서 정칙 함수는 편미분 $\partial f/ \partial z$가 바로 복소 미분 $df/dz$가 되며, $\bar z$에 대한 편미분은 항상 0이 되어서 $f(z)$는 $\bar z$ 요소를 가지고 있지 않다. 수학자 비르팅어Wilhelm Wirtinger(1865–1945)는 생소하지만, 비르팅어 교수가 가르친 제자 한 명은 매우 유명하다. 수학의 한계를 명확히 증명한 수학자 괴델Kurt Gödel(1906–1978)이 비르팅어 교수에게 수학을 배웠다.
복소수 $z$와 켤레 복소수 $\bar z$는 단순히 복소 평면에서 $x$축에 대칭인 두 점이라 생각하기 쉽지만, 복소 함수론 입장에서는 하늘과 땅만큼 차이가 있다. 복소수 $z$와 $\bar z$는 변화 특성이 확연히 다르다. 값 $x, y$를 증가시키면 $z$는 실수부와 허수부가 동시에 커진다. 하지만 $\bar z$는 실수부와 허수부의 증가 방향이 다르다. 이를 단위 벡터(unit vector)로 생각해서 $z$의 변화는 $\hat x, \hat y$, $\bar z$ 경우는 $\hat x, -\hat y$로 확연히 다르다. 아예 외적(outer product)을 도입해 $z, \bar z$의 방향을 각각 $\hat x \times \hat y$, $\hat x \times (-\hat y)$로 표현하기도 한다. 복소 함수가 가진 외적 특성은 2차원 그린 정리인 식 (14)에서도 관찰된다. 식 (14)에 나온 외적 성질은 그대로 코쉬–리만 방정식에 연결된다.
[극형식의 코쉬–리만 방정식(Cauchy–Riemann equation in polar form)]
 (1.4)
(1.4)여기서 $z$ = $x+iy$ = $r e^{i\phi}$이다.
[증명]
식 (6)에 나온 편미분에 $r, \phi$에 대한 완전 미분을 적용해서 해당 편미분을 다르게 기술한다.
 (1.5)
(1.5)여기서 $r$ = $\sqrt{x^2 + y^2}$, $\phi$ = $\tan^{-1}(y/x)$이다. 식 (1.5)를 식 (6)에 넣고 정리해서 식 (1.4)를 유도한다.
 (1.6)
(1.6)______________________________
식 (1.4)를 활용해서 극형식으로 된 복소 함수의 정칙 함수 여부를 쉽게 판정한다. 독립 변수 $(x, y)$를 변수 변환해서 $(r, \phi)$로 바꿀 때는 $\phi$방향에 주의한다. 변수 $\phi$는 마음대로 정의할 수 없고, 복소수의 외적에 부합하도록 $\hat x \times \hat y$ = $\hat r \times \hat \phi$로 정한다. 그래서 $\phi$는 반시계 방향으로 돌아야 하며, 이는 원통 좌표계(circular cylindrical coordinate system)를 구성하는 $\hat \phi$의 기준 방향도 된다.
2. 다양한 정리(various theorems)
유수 정리를 이용하면 다음에 있는 다양한 공식을 증명할 수 있다. 먼저 코쉬가 유수 정리와 함께 1831년코쉬 42세, 조선 순조 시절에 증명한 코쉬의 적분 공식을 살펴본다.
[코쉬의 적분 공식(Cauchy's integral formula)]
 (2.1)
(2.1)
여기서 $f(z)$는 코쉬–리만 방정식을 만족하는 정칙 함수이다.
[증명: 유수 정리]
복소 함수 $f(z)$는 정칙 함수이므로 자연스럽게 해석 함수가 된다. 그러면 식 (3)을 이용해 다음처럼 표현할 수 있다.
 (2.2)
(2.2)
따라서 식 (2.2)에 나타난 무한 급수의 유수는 식 (16)에 의해 $a_0$이므로, 식 (2.1)이 증명된다.
[증명: 적분 경로 변형]
복소 함수 $f(z)$가 정칙이라는 조건만 이용해서 적분 경로를 다음처럼 변경해본다.
 (2.3)
(2.3)
여기서 임의의 경로 $c$는 [그림 8]과 같은 적분 경로 변경을 통해 반지름 $R$인 원으로 바뀔 수 있다. 그러면 마지막 적분값이 $0$이어서 식 (2.1)을 증명할 수 있다.
______________________________
유수 정리를 이용한 증명이 적분 경로를 바꾼 경우보다 확실히 쉽다. 하지만 유수 정리를 쓸 때, 우리가 꼭 기억해야 하는 부분이 있다. 유수 정리는 정칙 함수가 필연적으로 해석 함수라는 조건으로 증명되었다. 그래서 식 (2.2)의 결과에도 해석 함수라는 조건을 사용한다. 이와는 다르게 식 (2.3)의 적분은 정칙 조건만 사용되고 해석 함수의 개념은 사용되지 않았다. 편해서 해석 함수 조건을 식 (2.2)에 썼지만, 식 (2.3)을 보면 코쉬의 적분 공식을 증명할 때는 정칙 조건만 있어도 된다. 이로 인해 정칙 함수가 해석 함수가 된다는 증명에 코쉬의 적분 공식을 적극적으로 사용한다.
코쉬의 적분 공식은 원주 상의 평균값 정리와 직접적으로 연결된다. 복소 함수가 가진 평균값의 특성은 가우스의 평균값 정리(Gauss' mean value theorem)라 한다.
[가우스의 평균값 정리(Gauss' mean value theorem)]
 (2.4)
(2.4)여기서 $r$은 임의의 반지름이다.
[증명]
 (2.5)
(2.5)
식 (2.1)에 있는 적분 경로를 중심이 $z_0$, 반지름이 $r$인 원주로 선택해서 적분한다.
 (2.5)
(2.5)______________________________
가우스의 평균값 정리를 더 확장해서 서로 다른 극형식(polar form)으로 표현된 적분간의 관계를 구할 수 있다. 복소 적분에서 극형식을 바꾸는 관계식은 푸아송의 적분 공식(Poisson's integral formula)이라 한다.
[푸아송의 적분 공식(Poisson's integral formula)]
 (2.6)
(2.6)여기서 $r \le R$이다.
[증명]
 (2.7)
(2.7)
적분 변수 $s$는 반지름 $R$인 원 위를 움직이고 $z$는 이 원의 내부점이라 생각한다. 그러면 다음과 같은 코쉬의 적분 공식이 성립한다.
 (2.7)
(2.7)여기서 $s$ = $R e^{i \varphi}$, $z$ = $r e^{i \phi}$이다. 원밖에 있는 점을 체계적으로 정의하기 위해 원에 대한 복소수의 역수(inverse of complex number) $z_i$를 도입한다.
 (2.8)
(2.8)역수 $z_i$는 $z$와 다르게 원밖에 있기 때문에 식 (2.7)과 같은 복소 적분은 $0$이 된다. 그래서 식 (2.7)에 $z_i$를 넣어서 약간 더 복잡하게 만든다. 복소 적분의 겉모양은 복잡해보이지만, 켤레 복소수의 관계가 나타나기 때문에 최종 결과는 간단해진다.
 (2.9)
(2.9)여기서 $|s - z|^2$은 코사인 제2 법칙(the second law of cosines)으로 구한다.
______________________________
식 (2.6)에서 복소 함수 $f(z)$를 제외한 나머지 피적분 함수는 실수이다. 그래서 식 (2.6)의 실수부만 선택해서 새로운 적분을 다음처럼 정의한다.
 (2.10)
(2.10)식 (2.10)을 이용해서 $(R, \varphi)$로 정의된 극형식을 $(r, \phi)$로 바꿀 수 있다. 비슷하게 식 (2.6)의 허수부만 선택해서 만든 적분으로 극형식을 교환하기도 한다.
식 (2.6)에서 $r$ = $0$이라 두면, 푸아송의 적분 공식은 가우스의 평균값 정리가 된다. 그래서 푸아송의 적분 공식은 극형식 입장에서 본 가우스 평균값 정리의 일반화이다.
[코쉬의 미분 공식(Cauchy's differentiation formula)]
 (2.11)
(2.11)
여기서 $f^{(n)}$은 복소 함수 $f(z)$를 $n$번 미분한다는 뜻이며 $f(z)$는 해석 함수이다.
[증명]
복소 함수 $f(z)$가 해석적이므로 다음 무한 급수로 미분을 표현할 수 있다.
 (2.12)
(2.12)
여기서 계수 $a_n$과 $f(z)$ 미분과의 관계는 테일러 급수 개념을 쓰면 쉽게 얻어진다. 그 다음에 식 (2.2)의 증명과 마찬가지로 식 (16)의 유수 정리를 쓰면, 식 (2.11)이 증명된다.
______________________________
식 (2.11)의 의미는 참 재미있다. 식 (2.11)은 복소 함수 $f(z)$가 $z$ = $z_0$ 근방에서 해석 함수라면 $z$ = $z_0$에서 무한번 미분 가능함을 의미한다. 이로 인해 해석 함수의 표면은 날카로운 부분없이 항상 부드럽고 매끈하다. 또한 복소 함수에서는 실제 미분할 필요없이 $z$ = $z_0$ 주변으로 선 적분하면 미분 계수가 얻어진다. 혹은 로랑 급수를 구할 때 선 적분을 통해 계수 $a_m$을 구할 수 있다는 뜻이다. 그래서 이 개념으로 식 (2.11)을 변형하면 다음 공식을 얻을 수 있다.
 (2.13)
(2.13)코쉬의 미분 공식에 의해 해석 함수를 $n$번 미분한 도함수도 저절로 해석 함수가 된다.
[해석 함수의 도함수(derivative of analytic function)]
복소 함수 $f(z)$가 해석적이면, 모든 고계 도함수(higher-order derivative) $f^{(n)}(z)$도 해석적이다.
식 (2.11)에 있는 코쉬의 미분 공식에 의해 모든 고계 도함수는 항상 연속이다. 가장 쉬운 출발점으로 1계 도함수 $f^{(1)}(z)$를 생각한다.
 (2.14)
(2.14)여기서 $f(z)$는 해석적이어서 [그림 5]처럼 1계 미분을 임의의 방향으로 할 수 있다. 1계 도함수 $f^{(1)}(z)$의 해석성을 다음과 같은 코쉬–리만 방정식으로 판정한다.
 (2.15)
(2.15)마찬가지 방법을 고계 미분에 쉽게 적용할 수 있으므로, 해석 함수의 모든 도함수는 항상 해석적이다.
______________________________
따라서 해석적인 복소 함수는 아무리 미분해도 뾰족해지지 않는 놀라운 성질이 있다.
복소 함수는 로랑 급수로 표현되기 때문에 극점이 $1 \mathbin{/} (z - z_0)$인 단순 극점 혹은 단순극(simple pole) 외에 분모의 차수가 2 이상인 다중 극점 혹은 다중극(multiple pole)을 가질 수 있다. 이 경우는 다중극의 유수 정리를 써서 유수를 구한다.
[다중극의 유수 정리(residue theorem of multiple pole)]
 (2.16)
(2.16)여기서 $f(z)$가 가진 극점의 최대 차수는 $k$이다.[$f(z)$의 특이점은 $1 \mathbin{/} (z - z_0)^k$ 비율로 변한다.]
[증명]
복소 함수 $f(z)$에 $(z-z_0)^k$를 곱해서 특이점을 없앤다. 이 경우 유수가 있는 $1 \mathbin{/}(z-z_0)$ 항은 차수가 $k-1$이다. 이 항의 계수를 구하기 위해 $k-1$번 미분하고 $z$ = $z_0$을 대입한다.
______________________________
닫힌 경로 $c$ 내부에 다중극이 여러 개인 때는 식 (16)처럼 각각의 유수를 계산해서 더한다.
[참고문헌]
[1] B. Riemann, Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse (Foundations for a General Theory of Functions of One Variable Size Complex Number), Inaugural Dissertation, University of Göttingen, Dec. 1851.
[2] A.-L. Cauchy, Mémoire sur les intégrales définies prises entre des limites imaginaires (Memorandum on Definite Integrals Taken Between Imaginary Limits), Académie des Sciences (Academy of Sciences), Feb., 1825.
[3] C. F. Gauss and F. Klein, Gauss' wissenschaftliches Tagebuch: 1796–1814 (Gauss' Scientific Diary: 1796–1814), Teubner, 1903.
[다음 읽을거리]






 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)
 (8)
(8) (9)
(9) (10)
(10)










 (10)
(10)

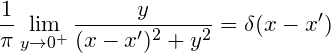





 (18)
(18)





 (21)
(21)