1. 발산의 의미
2. 전압
3. 전기장
[전기의 기초(electricity)]
[전기의 쉬운 이해]
전류(電流, electric current, $I$)는 말 그대로 전기의 흐름이다. 전기를 만드는 원천이 전하(電荷, electric charge, $Q$)이므로 전하의 흐름, 즉 전하의 시간($t$)적 변화율이라고 말할 수 있다. 이를 수식으로 표현하면 식 (1)이다.
(1)
식 (1)은 제대로 된 정의이기는 하나 전하의 흐름을 세부적으로 보여주지 못한다. 그래서 식 (1)을 미분 형태로 바꾼다. 이를 통해 전하의 미분소 $dQ$를 전하 밀도(電荷密度, charge density) $\rho$로 표현한다.
(2)
여기서 면적 미분소 $d \bar a$는 전류를 정의하기 위해 사용한 임의의 단면적(斷面積, cross-sectional area: 그림 1에서 $a$)이며 선 미분소 $d\bar l$은 전하가 실제로 지나간 방향의 통과 길이[그림 1에서 $l$]이다.
[그림 1] 도선에 흐르는 전류(출처: wikipedia.org)
체적 미분소 $dv$를 지나는 전하 미분소 $dQ$가 만드는 전류 미분소 $dI$는 아래와 같다.
(3)
여기서 벡터 $\bar u$는 전하의 유동 속도(流動速度, drift velocity)이다. 식 (3)으로부터 전체 면적을 통해 흐르는 총전류($I$)는 식 (4)가 된다.
(4)
식 (4)로부터 전하의 흐름을 세부적으로 표현할 수 있는 전류 밀도(電流密度, current density) $\bar J$의 중요성을 이해할 수 있다. 즉, 식 (4)로부터 전류 밀도의 방향은 전류가 흐르는 방향이 됨을 알 수 있다.
[전하 보존 법칙(conservation of electric charge)]
전류 밀도($\bar J$)의 원천을 검출하면 그 값은 전하 밀도($\rho$)의 시간적 감소와 같다.
(5)[증명]
식 (5)를 체적 적분하고 발산 정리를 적용하면 식 (6)을 얻을 수 있다.
(6)
식 (6)의 좌변은 우리가 적분에 사용한 체적을 빠져나가는 전류[∵ 식 (4)로부터 전류 밀도와 면적 미분소의 내적은 전류이며 면적 미분소의 벡터 방향은 해당 체적을 뚫고 나가는 방향이다.]를 뜻한다. 식 (6)의 우변은 이 경우 체적에 존재하는 전하($Q$)는 그만큼 시간적으로 줄어듦을 의미한다. 식 (6)의 좌변과 우변은 서로 같으므로 식 (5)가 전하 보존 법칙을 의미함이 증명된다.
______________________________
전하 보존 법칙은 쿨롱의 법칙(Coulomb's law)이 제안되기 전에 프랭클린Benjamin Franklin(1706–1790)이 최초로 발견해서 1751년에 영국 왕립학회(The Royal Society)의 논문으로 발표했다. 마찰시키면 전기를 얼마든지 만들 수 있다는 사람들의 믿음과 달리, 프랭클린은 전기를 이송하는 실험[한 곳의 전기를 다른 곳으로 보내면, 원래 있던 전기가 줄어드는 현상을 확인]을 통해 전하 보존성을 찾아냈다. 미국 국부(國父, Founding Fathers) 중 한 명인 프랭클린은 다재다능해서 인쇄공, 발명가, 작가, 정치인 등의 분야에서 모두 성공했다. 전기의 근원에도 관심이 많아서 진짜 목숨을 걸고 피뢰침(避雷針, lightning rod)을 발명했다.
_-_Benjamin_Franklin_Drawing_Electricity_from_the_Sky_-_Google_Art_Project.jpg)
[그림 2] 하늘로부터 전기를 이끌어내는 프랭클린(출처: wikipedia.org)
식 (5)에 나오는 전하 밀도는 전류 밀도를 만들어내야 하므로, 정확히는 자유 전하 밀도(free charge density)로 불러야 한다. 자유 전하는 물질 속을 자유롭게 돌아다니면서 전기를 이송할 수 있는 근원이다. 자유 전하에 반대되는 개념은 물질에 묶여서 분극(polarization)을 일으키는 구속 전하(bound charge)가 있다. 쉽게 말해 금속에는 자유 전하가 전기를 이송하고, 유전체에는 구속 전하만 있어서 전기를 흘리지 못한다.
[그림 3] 키르히호프 전류 법칙(출처: wikipedia.org)
[키르히호프의 법칙(Kirchhoff's laws)]
[키르히호프 전류 법칙(KCL: Kirchhoff Current Law)]
(7)
식 (6)에서 DC(직류, 直流, Direct Current) 조건을 적용하면 식 (7)이 바로 얻어진다. DC 조건은 시간적 변화[= $\partial / \partial t$]가 0이라는 조건이다.
______________________________
DC 조건인 경우 식 (7)을 전류 밀도의 경계 조건(boundary condition) 관점으로 살펴본다. 어떤 체적 $\Delta V$의 전하 축적이 없는 경우 식 (7)에 의해 들어간 전류[$I_1$ = $J_{n1} \Delta S_1$]와 나간 전류[$I_2$ = $J_{n2} \Delta S_1$]는 반드시 같아야 한다[$I_1$ = $I_2$]. 체적 $\Delta V$를 원기둥[$\Delta S_1$ = $\Delta S_2$]이라 가정하고 식 (6)을 이용해 $I_1$ = $I_2$를 전류 밀도 관점에서 쓰면 $J_{n1}$ = $J_{n2}$가 되므로, 전류 밀도의 법선 성분은 반드시 연속이 되어야 한다. 여기서 전하 축적은 커패시터(capacitor)의 전기 용량(capacitance) 때문에 생기므로 전하 축적이 없다는 말은 커패시터 성분이 없음과 같은 말이다.
[표 1] 물질별 전기 전도도(출처: wikipedia.org)
| 물질 (Substance) | 전기 전도도 (S/m) (Electrical conductivity) | 온도 계수 (1/K) (Temperature coefficient) | 기타 사항 (Other details) |
|---|---|---|---|
| 테플론(Teflon, PTFE) | $10^{-25}$–$10^{-23}$ | - | - |
| 규소(silicon) | 4.35 × $10^{-4}$ | -75 × $10^{-3}$ | - |
| 바닷물(sea water) | 4.8 | - | - |
| 철(iron) | 1.03 × $10^7$ | 5.00 × $10^{-3}$ | - |
| 알루미늄(aluminum) | 3.77 × $10^7$ | 3.90 × $10^{-3}$ | - |
| 금(gold) | 4.11 × $10^7$ | 3.40 × $10^{-3}$ | - |
| 구리(copper) | 5.96 × $10^7$ | 4.04 × $10^{-3}$ | - |
| 은(silver) | 6.30 × $10^7$ | 3.80 × $10^{-3}$ | - |
전압에 대한 조건인 KVL(Kirchhoff Voltage Law)과 전류에 대한 조건인 KCL(Kirchhoff Current Law)은 회로 이론에서 매우 중요한 법칙이다. 이와 더불어 굉장히 중요한 회로 법칙인 옴의 법칙(Ohm's Law)을 증명해본다.
[옴 법칙의 미분형(Ohm's law in differential form)]
(8)
여기서 $\sigma$는 전기 전도도(電氣傳導度, electrical conductivity: 물질의 고유한 특성)[단위: S/m] 혹은 간단히 전도도라 부른다.
[증명]
식 (8)을 증명하기 위해서는 전하가 도선을 흐르는 특성을 고려해야 한다. 1897년톰슨 41세, 대한제국 원년 톰슨Joseph John Thomson(1856–1940)은 음극선관(cathode-ray tube)을 이용해 전자(電子, electron)의 존재를 실험적으로 증명했다. 그래서 톰슨의 실험으로 인해 전류를 구성하는 입자는 전자임이 분명해졌다. 전자가 만드는 전류의 특성은 보통 식 (8)로 기술한다. 옴 법칙의 미분형인 식 (8)을 증명하려면 전자가 도선에서 받는 힘을 정량화해서 표현해야 한다. 이 기법을 성공적으로 적용한 최초의 학자는 드루데Paul Drude(1863–1906)이다. 드루데가 1900년드루데 37세, 대한제국 시절에 제안한 방법인 드루데 모형(Drude model) 혹은 자유 전자 모형(free electron model)을 이용하여 식 (8)을 증명한다[1], [2].
[그림 4] 도선 속에 있는 전자의 운동(출처: wikipedia.org)
도선을 따라 전자가 흐르면 [그림 4]와 같이 결정(結晶, crystal) 속을 따라 전자가 이동한다. 이때 결정을 구성하는 매우 무거운 양성자(陽性子, proton)로 인해 전자는 계속 이동하지 못하고 반대 방향으로 튕기게 된다. 이 상황을 뉴턴의 제2 운동 법칙(Newton's second law of motion)으로 표현하면 식 (9)와 같다.
(9)
여기서 벡터 $\bar p_n$은 $n$번째 전자의 운동량(運動量, momentum)이며 $\gamma$는 견인 계수(牽引係數, drag coefficient)이다. 식 (9)를 좀더 자세히 설명하면 $n$번째 전자가 받는 힘은 운동을 방해하는 방향[식 (9)에 (-)가 있는 이유]으로 작용하는 견인력(牽引力, drag force)이다.[물속을 이동하는 물체를 고려한다. 이 물체는 유체(fluid)에 의해 견인력 혹은 저항력을 느낀다. 실험에 의하면 물체 이동 속도가 느린 경우 견인력은 속도에 비례한다. 이를 운동량으로 표현하면 식 (9)처럼 된다.] 도선에 생기는 견인력의 원인은 양성자와 전자 사이에 생기는 전기력(electric force)이다. 또한 견인력은 전자가 받는 운동량에 비례한다. 전자에 작용하는 견인력으로 인해 [그림 4]처럼 전자가 튕기게 된다. 식 (9)에 있는 미분 방정식을 풀면 식 (10)을 얻을 수 있다.
(10)
여기서 벡터 $\bar C_n$은 임의의 적분 상수이다. 식 (10)처럼 시간이 흐르면 전자의 운동량은 기하급수적으로 줄어든다. 식 (9)는 전자 하나에 대한 운동 방정식이므로, 각 전자의 기여를 모두 모아서 평균을 낸다. 그러면 다음처럼 도선 속에 있는 전체 전자의 평균 운동량을 얻을 수 있다.
(11)
외부힘이 없는 상태에서는 도선 속에 있는 전자는 평균적으로 힘을 전혀 받지 않기 때문에 식 (11)의 둘째줄이 반드시 성립해야 한다. 만약 전자가 평균적으로 힘을 받는다면 이 힘을 외부에서 사용할 수 있기 때문에 현실과 맞지 않게 된다. 식 (11)에서 외부 전기장 $\bar E$가 가해지면 식 (11)은 아래와 같이 변형되어야 한다.
(12)
여기서 $e$는 전자의 전하량이다. 식 (12)에서 시간이 무한대로 흐르면, 외부 전기장에 의해 전자의 운동량 평균은 0이 아닌 값으로 수렴한다. 이 값을 식 (13)과 같이 계산할 수 있다.
(13)
여기서 $m_e$는 전자의 질량(質量, mass)이다. 전기 이동도(electrical mobility) $\mu_e$ 관점으로 식 (13)을 쓰면, $\bar u_f$ = $- \mu_e \bar E$라 할 수 있다.[$\mu_e$ = $e / (\gamma m_e)$] 전기 이동도 $\mu_e$는 사실 전자가 만들기 때문에, 전자 이동도(electron mobility)라 할 수도 있다. 식 (13)의 둘째식을 $0$으로 둔 이유는 시간이 무한대로 흐르면 전자 운동이 안정화되어 더 이상의 운동량 변화는 없기 때문이다. 즉, 전기장을 가하면 처음에는 전자가 가속받아 운동량이 증가하지만, 시간이 한없이 지나면 정상 상태(正常狀態, stationary state)가 되어 더 이상의 속도 변화는 없어진다. 식 (12)에 있는 미분 방정식은 쉽게 풀리는 방정식이다. 식 (10)과 (13)을 고려하면 식 (12)의 해는 식 (14)와 같다.
(14)
식 (14)를 식 (12)에 대입해서 정리하면 쉽게 해가 됨을 증명할 수 있다. 전자의 유동 속도를 나타내는 $\bar u$는 전자의 실제 속도가 아니다. [그림 4]와 같이 전자의 실제 속도는 매우 빠르나 양성자에 부딪혀 얼마가지 못하고 반대 방향으로 가기 때문에 등가적으로 측정되는 전진 속도인 유동 속도는 그리 빠르지 않다. 이 유동 속도를 식 (4)의 좌변에 대입하면 식 (8)이 얻어진다.
(15)
여기서 전하 농도(charge concentration) $n_e$는 전자의 단위 부피당 개수[= $N/V$]이다. 전기 이동도 $\mu_e$를 사용하면, 전도도($\sigma$)는 $e n_e \mu_e$가 된다. 농도 $n_e$는 물질의 고유 특성으로서 밀도, 몰 질량(molar mass) 및 아보가드로 수(Avogadro constant, $N_A$)에 의해 결정된다.
______________________________
견인 계수 $\gamma$는 식 (10)이나 (14)와 같이 시간($t$)의 역수와 관계되므로 식 (16)처럼 바꾸어쓴다.
(16)
(17)
식 (17)이 제대로 된 확률인지 확인하기 위해 식 (18)을 계산한다. 전체 확률값이 $1$이 되므로, 식 (17)은 확률 관점으로 잘 정의된다.
(18)
식 (17)을 이용하여 시간의 기대값(expectation)을 계산하면 식 (19)가 된다.
(19)
그런데, 시간의 기대값은 무슨 의미인가? 정의된 확률이 운동량을 기준으로 제시되므로, 시간의 기대값은 전자의 운동량이 존재하는 평균 시간이 된다. 그래서 $\tau$는 전자가 양성자에 부딪히지 않고 진행할 수 있는 평균 시간을 뜻하게 된다.
[옴의 법칙(Ohm's law)]
[옴의 법칙(Ohm's law)]
(20)
여기서 $R$은 저항(抵抗, resistance)[단위: 옴(ohm, Ω)]이다.
[증명]
미분형 옴의 법칙인 식 (8)로부터 식 (20)을 쉽게 증명할 수 있다. 먼저 식 (4)로부터 유도를 시작한다.
(21)
여기서 전류 밀도 $\bar J$와 면적 미분소 $d \bar a$는 같은 방향으로 잡아서[∵ 전류가 뚫고 지나가는 단면적은 우리 임의대로 잡을 수 있다. 즉, 단면적이 어떤 모양으로 있든지 전류 밀도 $\bar J$만 적절히 포함하면 흐르는 전류 $I$는 동일하다.] 벡터를 사용하지 않고 스칼라를 사용하였다.[∵ 내적을 구성하는 벡터가 같은 방향이면 두 벡터 크기의 곱으로 생각할 수 있다.] 전압과 전기장의 관계로부터 식 (22)가 정의된다.
(22)
여기서도 전기장 $\bar E$의 방향과 선 미분소 $d \bar l$의 방향을 동일하게 잡았다.[∵ 전기장을 정의하는 선 미분소의 방향도 우리가 임의로 잡을 수 있다.] 이와 같은 방식으로 전류 밀도, 전기장, 면적 미분소, 선 미분소가 동일한 벡터 방향을 가지게 만들 수 있다.[면적 미분소와 선 미분소의 방향이 같기 때문에 면적 미분소와 선 미분소의 단순곱은 정확히 공간을 이루는 부피 미분소($dv$ = $da\cdot dl$)가 된다.] 식 (22)를 식 (21)에 대입하여 전압 미분소 $dV$를 다음처럼 구한다.
(23)
여기서 전압 미분소 $dV$는 적분을 빠져 나올 수 있도록 단면적 $s$에 대해 상수로 정했다. 이 부분을 이해하기 위해 다음과 같이 생각한다. 선 미분소 $dl$의 방향은 전류 밀도 방향과 동일하게 잡았기 때문에, 선 미분소 방향으로만 전류가 흐른다. 그러면 미분형 옴의 법칙에 의해 전류가 흐르는 방향으로만 전기장이 생긴다. 이는 면적 미분소가 표현하는 단면적 방향으로만 전기장이 생긴다는 뜻이므로,[∵ 이 단면적에서는 등전위면(等電位面, equipotential surface)이 된다. 등전위면이 변화할 수 있는 유일한 방향은 길이 $l$방향이다.] 단면적 $s$ 상의 전압 $V$는 다음처럼 항상 상수가 된다.
(24)
여기서 $t_1$, $t_2$는 단면적 $s$를 구성하는 좌표 성분이다. 또한 $dl$은 전압이 최대로 변하는 방향이므로, $dl$을 잘 정의하면 단면적 $s$ 상에서 전압 미분소 $dV$가 상수가 되게 할 수 있다. 전체 전압을 구하기 위해 식 (23)을 길이 $l$에 대해 적분하면 최종식 (25)가 얻어진다.
(25)
여기서 $I$가 적분을 빠져나오는 이유는 선 미분소의 방향을 전류 방향과 동일하게 잡았으므로 전하 보존 법칙에 의해 들어간 전류는 나간 전류와 동일해서[혹은 KCL이 성립해서] 길이 $l$에 대해 상수로 취급할 수 있기 때문이다.
______________________________
식 (20)의 증명 시작은 식 (21)의 전류($I$)부터 하였다. 이와는 다르게 식 (22)의 전압($V$)부터 출발하면 식 (25)와 동일한 결과를 얻을 수 있을까? 이런 방식은 불가능하다. 전류는 전압과는 다르게 식 (24)의 등전위면과 유사한 정의를 할 수 없기 때문이다. 즉, 일반적으로 전류밀도는 전압을 정의한 선적분 바깥으로 나갈 수 없기 때문이다.
원론적으로 저항은 식 (26)으로 정의할 수 있다.
(26)
하지만, 식 (26)은 전기장 $\bar E$가 결정되지 않으면 계산될 수 없다. 따라서, 식 (25)가 저항 계산에 매우 유용한 공식이다.
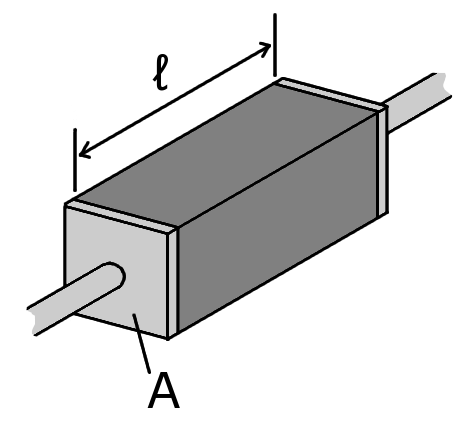
[그림 5] 단순 저항기의 구조(출처: wikipedia.org)
예를 들어 [그림 5]처럼 전류가 $z$방향으로 흐르고 전도도가 일정하면, 저항 $R$은 식 (27)과 같이 얻어진다.
(27)
여기서 $l$은 저항의 길이, $A$는 저항의 단면적이다. 식 (25)에서 단면적 $s$와 길이 $l$을 구성하는 좌표계가 직교한다면, 직교 좌표계의 척도 인자(尺度因子, scale factor)를 사용하여 식 (25)를 다음처럼 간략화할 수 있다.
(A.1)
(A.1)
앞에서 정의한 전압(voltage), 전류(current), 저항(resistance)을 이용하면 전기 회로가 소비하는 전력을 정의할 수 있다. 먼저 전압의 정의를 이용해 전기 회로가 사용하는 일(work)은 다음처럼 정한다.
(28)
식 (28)을 미분하면 다음을 얻는다.
(29)
직류가 흐르는 전기 회로에서는 전압의 변화($dV$)가 없기 때문에 $dV$ = $0$이 된다. 이런 조건하에서 식 (29)를 시간 미분인 $dt$로 나누면 전기 회로의 전력(electric power of an electrical circuit)을 다음처럼 정의할 수 있다.
(30)
식 (30)에 옴의 법칙을 적용하면 저항 기반의 전력 공식도 유도할 수 있다.
(31)고전 역학의 기본 언어는 힘(force)과 에너지(energy) 혹은 일률이지만, 회로 이론에서는 물성을 더 세밀히 설명하는 전류와 전압이 중심이고 필요한 경우 식 (31)을 이용해 전력으로 환산한다.
[참고문헌]
[1] P. Drude, "Zur Elektronentheorie der Metalle (On the electron theory of metals)," Annalen der Physik (Annals of Physics), vol. 306, no. 3, pp. 566–613, 1900.
[2] E. M. Purcell and D. J. Morin, Electricity and Magnetism, 3rd ed., Cambridge University Press, 2013.
[3] B. R. Russell, "Surface charges on conductors carrying steady currents," Am. J. Phys., vol. 36, no. 6, pp. 527–529, Jun. 1968.
[4] A. K. T. Assis, W. A. Rodrigues, and A. J. Mania, "The electric field outside a stationary resistive wire carrying a constant current," Found. Phys., vol. 29, no. 5, pp. 729–753, May 1999.
[5] T. Sauer, "Einstein and the early theory of superconductivity, 1919–1922," Arch. Hist. Exact Sci., vol. 61, no. 2, pp. 159–211, Mar. 2007.
[6] F. London and H. London, "The electromagnetic equations of the supraconductor," Proc. R. Soc. Lond. A, vol. 149, no. 866, pp. 71–88, Mar. 1935.
[다음 읽을거리]
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(2)
(3)
(4)
(5)
(5)
(6)