분수 차원을 가진 프랙탈(Fractal with Fractional Dimension)

[경고] 아래 글을 읽지 않고 "분수 차원을 가진 프랙탈"을 보면 바보로 느껴질 수 있습니다.

1. 바이어슈트라스 함수

[그림 1] 프랙탈 도형의 예(출처: wikipedia.org)

임의 공간의 차원(dimension)은 공간을 구성하는 독립적인 기저(basis)의 개수로 정한다. 2차원 공간에서 기저 벡터(basis vector)는 $\hat x, \hat y$ 2개라서 2차원, 3차원 공간은 $\hat x, \hat y, \hat z$로 구성해서 3차원 등과 같은 논리로 공간의 차원을 정확하게 규정할 수 있다. 조금 더 나가서 공간의 차원을 자연수가 아닌 분수로 표현할 수 있을까? 자연수를 분수로 더 확장하는 개념은 상식적이지만, 공간 차원의 분수 표현은 전혀 다른 문제가 된다. 여기서 중요한 부분은 자연수를 분수로 바꾸는 개념보다는 공간의 차원을 어떻게 비틀어야 분수 차원을 합리적으로 정의할 수 있는가이다. 자연수로 된 개념을 분수로 확장하는 문제는 어떤 분야든지 참 재미있다. 예를 들면 미분과 적분은 한 번, 두 번과 같은 자연수 기반 연산이다. 통상적인 미적분을 분수 미적분학(fractional calculus)으로 바꾸려면 연산자를 보는 새로운 관점인 연산 미적분학(operational calculus)과 같은 탁월한 개념이 필요하다.

분수 미적분학과 비슷하게 특이한 분수 차원을 만들려면 이전 벡터 공간의 특성을 포함하면서도 논란 없이 공간을 규정하는 새로운 차원 정의가 필요하다. 새로움은 옛것을 바라보는 별난 관점이기도 해서, 다음과 같은 도형의 척도(scale)와 자기 유사성(self-similarity) 관계를 생각해보자.

[그림 1] 정수 차원을 정의하기 위한 척도와 자기 유사성(출처: wikipedia.org)

[그림 1]을 보면 기본 도형을 특정 척도로 계속 줄여서 자기 유사성을 가진 도형을 만들어서 자기와 닮은 도형의 개수를 헤아린다. 1차원인 경우, 길이가 $1$인 직선을 특정 척도에 따라 줄여서 자기 유사성이 있도록 한다. 줄어든 직선이 서로 자기 유사성을 가지는 척도 $\epsilon$은 $1/2, 1/3, 1/4, \cdots$만 가능하다. 그러면 얻어지는 직선의 개수 $N$은 $2, 3, 4, \cdots$이다. 척도와 자기와 닮은 도형의 개수를 조합해서 $2$ = $(1/2)^{-1}$, $3$ = $(1/3)^{-1}$ 등을 얻을 수 있다. 2차원에서는 면적이 $1$인 사각형을 척도에 따라 줄여서 자기 유사성이 있는 사각형을 만든다. 예를 들어 $\epsilon$ = $1/2$이라면 [그림 1]에 의해 $N$ = $4$이다. 그래서 $4$ = $(1/2)^{-2}$이 된다. 이러한 개념을 공간의 차원 $D$에 대한 일반 공식으로 쓰면 다음과 같다.

                  (1)

식 (1)에서 자기와 닮은 도형의 개수 $N$은 어떤 자연수의 거듭제곱이다. 그런데 공간의 차원을 정할 때, 거듭제곱 특성을 반드시 만족할 필요가 있을까? 척도에 따라 늘어나는 닮은 도형의 개수가 자연수의 거듭제곱이 아니어도 되면, 공간의 차원은 분수나 무리수가 될 수 있다. 공간의 차원이 자연수가 아닌 공간은 프랙탈(fractal)이라 한다. 프랙탈이란 기하학적 개념은 망델브로Benoit Mandelbrot(1924–2010)가 1975년망델브로 51세, 박정희 정부 시절에 제안했다. 프랙탈의 어원은 깨진 혹은 파편화된을 뜻하는 라틴어 프락투스(fractus)이다. 이 어원에서 분수(分數, fraction)가 나오므로, 프랙탈은 분수 관계[영어에서 접미사 -al은 디지털(digital)이나 동물(animal)처럼 관계성을 표현한다.]로 직역할 수 있다. 또한 프랙탈 공간의 차원은 프랙탈 차원(fractal dimension)이라 축약해서 부른다.

   1. 곡선(curve)   

[코흐 곡선(Koch curve)]

코흐 곡선(Koch curve) 혹은 코흐 눈송이(Koch snowflake)는 연속이지만 접선이 존재하지 않는 신기한 곡선이다. 코흐 곡선의 제안자인 코흐Helge von Koch(1870–1924)는 적분 방정식(integral equation)의 일반 해법을 최초로 제시한 프레드홀름 적분 방정식(Fredholm integral equation)의 핵심 도구인 무한 행렬식(infinite determinant)을 연구해 박사 학위를 받았다.

[그림 1.1] 코흐 눈송이의 생성 예(출처: wikipedia.org)

코흐 곡선은 다음과 같은 간단한 절차로 만들 수 있다.

• 현재 직선을 같은 간격으로 3등분한다.
• 3등분 중에서 중간에 있는 직선에 정삼각형을 그린다.
• 정삼각형의 밑변을 지운다.
• 줄어든 직선 각각에 대해 위 과정을 계속 반복한다.

코흐 곡선은 $\epsilon$ = $1/3$할 때 $N$ = $4$개의 자기와 닮은 직선이 생긴다. 그래서 코흐 곡선의 프랙탈 차원은 $D$ = $\log(4)/\log(3)$ $\approx$ $1.26$이다. 직선과 평면 사이의 차원이지만 직선에 조금 더 가깝다. 길이가 $L$인 직선으로 코흐 곡선 만들기 과정을 $n$번 하면 전체 길이는 다음과 같다.

                  (1.1)

따라서 $n \to \infty$라면 코흐 곡선의 길이는 무한대가 된다. 또한 코흐 곡선에서 인접한 점은 항상 변하고 있어서 모든 점에서 접선을 정의할 수 없다. 이러한 코흐 곡선의 특징은 바이어슈트라스 함수(Weierstrass function)와 매우 닮아있다. 수학적으로 탄탄한 증명이 있는 바이어슈트라스 함수도 연속이지만 모든 점에서 미분 불가능이다. 바이어슈트라스 함수의 성질은 매우 수학적이어서 상상이 어렵지만, 코흐 곡선은 매우 간단한 원리로 생성이 가능해서 연속인 미분 불가능 함수를 기하학적으로 쉽게 표현할 수 있다.

   2. 표면(surface)   

[시에르핀스키 삼각형(Sierpiński triangle)]

시에르핀스키 삼각형(Sierpiński triangle) 혹은 시에르핀스키 개스킷(Sierpiński gasket)은 공간을 차지하고 있지만 면적인 $0$인 2차원 도형이다.

[그림 2.1] 시에르핀스키 삼각형의 생성 예(출처: wikipedia.org)

시에르핀스키 삼각형은 다음과 같이 생성한다.

• 현재 정삼각형의 각 변을 2등분한다.
• 각 변의 이등분점을 이어서 더 작은 정삼각형 4개를 만든다.
• 중앙에 위치한 정삼각형을 지운다.
• 줄어든 정삼각형 각각에 대해 위 과정을 계속 반복한다.

시에르핀스키 삼각형은 척도 $\epsilon$ = $1/2$가 될 때, 생성된 정삼각형의 개수 $N$은 $3$이다. 식 (1)에 대입해서 구한 프랙탈 차원은 $D$ = $\log(3)/\log(2)$ $\approx$ $1.58$이다. 코흐 곡선과는 다르게 시에르핀스키 삼각형은 2차원 평면에 더 가깝다. 하지만 시에르핀스키 삼각형의 면적은 희한한 특성이 있다. 처음 시작한 정삼각형의 면적을 $A$라 하고 생성 과정을 반복한 회수를 $n$이라 하면, 남아있는 삼각형의 면적 $A_n$은 다음과 같다.

                  (2.1)

반복 회수 $n$을 무한대로 보내면, 식 (2.1)에 의해 시에르핀스키 삼각형은 면적이 없어지게 된다. 하지만 전체 변의 길이는 면적과는 전혀 다른 특성을 보인다. 처음 정삼각형의 한 변을 $a$라 할 때, 생성을 $n$번 반복한 삼각형이 가진 전체 변의 길이 $L_n$은 다음처럼 표현된다.

                  (2.2)

따라서 시에르핀스키 삼각형은 변의 길이가 무한대로 발산하지만 면적 자체는 없는 이상한 도형이 된다. 이러한 비정상적인 도형의 특성을 자기 유사성을 바탕으로 분석하는 유용한 도구가 프랙탈이라는 개념이다.

[참고문헌]

[1] J. Cepelewicz, "The quest to decode the Mandelbrot set, math’s famed fractal," Quanta Magazine, Jan. 2024. (방문일 2024-02-01)

바이어슈트라스 함수(Weierstrass Function)

[경고] 아래 글을 읽지 않고 "바이어슈트라스 함수"를 보면 바보로 느껴질 수 있습니다.

1. 극한과 연속성의 의미

2. 푸리에 급수의 시작

[그림 1] 바이어슈트라스 함수의 생성 예(출처: wikipedia.org)

함수의 연속성(continuity)과 미분 가능성(differentiability)의 차이는 고등학생 수준의 지식만 있어도 충분히 이해할 수 있다. 예를 들어 절대값(absolute value) 함수 $|x|$는 연속이지만 $x$ = $0$에서는 미분이 불가능하다.

[그림 2] 절대값 함수의 변화(출처: wikipedia.org)

그래서 연속성이 더 큰 개념이고 미분 가능성은 함수가 연속이 되기 위한 충분 조건일 뿐이라고 확언할 수 있다. 하지만 이런 수준의 결과에 만족하면, 우리의 사고가 정지해서 더 전진할 수가 없다. 사소한 부분에도 고민이 많은 수학자가 되어보자. 수학자는 한 점에서의 미분 불가능성에 만족해서 물러나지 않는다. 예를 들어 조각마다 미분 가능(piecewise differentiability)이란 개념을 만들어서 [그림 2]처럼 $x$ = $0$에 있는 미분 불가능점을 제외해본다. 그러면 연속성과 미분 가능성은 동등하다 혹은 같다고 주장할 수도 있다. 조각마다 미분 가능에 대한 추론이 정말 맞을까? 이 질문에 답하기 위해 미분 불가능점을 제거해도 소용이 없는 방법을 고안해야 한다. 특정 구간에서는 연속이지만 구간 내에서 항상 미분이 불가능한 함수를 꼭 찾아서 반론을 제기해야 한다. 문제의 해결책이 보이지 않을 때는 우리 관점을 약간 바꾸어서 관조할 필요도 있다. 함수 연속성의 반대인 불연속을 생각해보자. 푸리에 급수(Fourier series)는 매우 독특한 성질이 있다. 상식적인 관점에서 연속인 삼각 함수를 무한 번 더하더라도 결과는 연속 함수가 되어야 정상이다. 하지만 어떤 경우에는 연속 함수로 구성한 푸리에 급수의 합이 불연속 함수를 표현할 수도 있었다. 처음에는 불연속 함수를 표현하는 푸리에 급수가 틀렸다고 오판했다. 하지만 뚝심있는 푸리에Joseph Fourier(1768–1830) 덕분에 푸리에 급수는 수학적 상상력을 폭발시킨 발화점이 되었다. 잘 보면 푸리에 급수가 연속과 불연속을 표현할 수 있기 때문에, 불연속과 밀접한 관계가 있는 함수의 미분 불가능성도 푸리에 급수로 풀 수 있을지도 모른다. 그래서 푸리에 급수와 같은 무한 급수(infinite series)를 이용해서 함수의 연속성과 미분 가능성을 심도있게 연구하게 되었다. 즉 모든 점에서 연속인 미분 불가능 함수(continuous non-differentiable function)를 찾으려 리만Bernhard Riemann(1826–1866)을 포함한 여러 수학자가 노력하였다[2]. 수학의 영웅 중 한 명인 리만은 다음과 같은 푸리에 급수를 고민했다.

                  (1)

무한 급수 $\sum_{n = 1}^\infty 1/n^2$은 절대 수렴(absolute convergence)하기 때문에 식 (1)도 절대 수렴한다. 또한 사인 함수는 $|\sin(x)|$ $\le$ $1$을 만족하므로, 바이어슈트라스 $M$판정(Weierstrass $M$-test)에 의해 식 (1)은 균등 수렴(uniform convergence)한다. 즉 식 (1)에 나온 $f(x)$는 매우 잘 정의되는 연속 함수이다. 다음 단계로 $f(x)$를 미분해보자. 함수 $f(x)$의 미분이 항별 미분과 같을지는 잘 모르지만, 대충 항 별로 미분하면 다음 결과를 얻는다.

                  (2)

식 (2)의 부분 합은 항을 더함에 따라 계속 진동하므로, 식 (2)는 수렴하지 않는다. 하지만 이와 같은 논증에는 약간의 문제가 있다. 식 (2)는 식 (1)의 미분 $df(x)/dx$인지 증명되지 않았고, 식 (2)의 부분 합은 분명 진동하지만 유계인지 무한대로 발산하는지도 모호하다. 이런 너저분한 상황을 깔끔하게 정리하는 사람이 진정한 수학자이다. 바이어슈트라스Karl Weierstrass(1815–1897)는 1872년바이어슈트라스 57세, 조선 고종 시절에 다음과 같은 바이어슈트라스 함수(Weierstrass function) $W(x)$를 발표하여 연속성과 미분 불가능성 개념을 확실히 정립했다.

                  (3)

식 (1)과 마찬가지로 바이어슈트라스 함수는 절대 수렴하고 바이어슈트라스 $M$판정에 의해 균등 수렴도 한다. 즉 바이어슈트라스 함수도 전영역에서 연속이다. 연속성은 쉽게 유도했지만, $W(x)$의 미분은 절대 쉽지 않다. 일단 항별 미분의 합이 균등 수렴하는지 알 수 없기 때문에, 기본으로 돌아가서 다음과 같은 무한 급수에 대한 기울기 정의를 이용해 미분한다.

                  (4)

좌극한과 우극한을 따로 구하기 위해 임의의 고정점 $x$ = $x_0$를 이용해 $\alpha_m$과 $\beta_m$을 각각 정의한다[1].

                  (5)

여기서 $m$은 자연수, 정수인 $k_m$은 $\chi_m$이 구간 $(-1/2, 1/2]$ 사이에 있도록 정한다. 식 (5)에 의해 $\alpha_m$과 $\beta_m$은 $x_0$의 왼쪽과 오른쪽에 각각 위치한다.

                  (6)

식 (6)에 의해 $m$을 계속 키우면, 간격 $\beta_m - \alpha_m$ = $1/b^m$은 $0$으로 수렴해서 $x_0$에 접근시킬 수 있다. 다음 단계로 변수 $\alpha_m$을 이용해 $W(x_0)$의 왼쪽 기울기를 구한다.

                  (7)

유한 급수 $S_1$과 무한 급수 $S_2$는 특성이 서로 달라서 각각 최종 합을 유도한다. 먼저 삼각 함수의 합차 공식을 이용해서 $|S_1|$의 한계를 정한다.

                  (8)

무한 급수 $S_2$를 계산하기 위해 다음 항을 미리 계산한다.

                  (9)

                  (10)

식 (9)와 (10)을 $S_2$에 대입해서 정리한다.

                  (11)

식 (11)에 있는 무한 급수의 항은 항상 $0$보다 크기 때문에, 무한 급수는 초항보다 항상 크거나 같다.

                  (12)

여기서 식 (5)에 의해 $\chi_m$은 $(-1/2, 1/2]$ 범위에 있다. 식 (8), (11), (12)를 합쳐서 왼쪽 기울기의 변화를 얻는다.

                  (13)

여기서 $S_2$와 관계된 $A$는 $A \ge 1$, $S_1$을 위한 $\epsilon_s$는 $(-1, 1)$ 사이에 있다. 식 (13)에 있는 $A + \epsilon_s$는 항상 $0$보다 커서 왼쪽 기울기의 부호는 $k_m$이 결정한다. 또한 $m \to \infty$로 보내면 왼쪽 기울기의 크기는 발산한다. 비슷한 방법으로 $x$ = $x_0$에서 오른쪽 기울기를 계산한다.

                  (14)

유한 급수 $T_1$과 무한 급수 $T_2$의 한계는 다음과 같다.

                  (15)

                  (16)

따라서 오른쪽 기울기가 가진 성질을 다음처럼 표현할 수 있다.

                  (17)

여기서 $B > 1$, $\epsilon_t \in (-1, 1)$, $B + \epsilon_t > 0$이다. 식 (17)에서 $m$이 커지면, 오른쪽 기울기의 크기는 발산하고 부호는 왼쪽 기울기와 반대가 된다. 따라서 $x$ = $x_0$에서 미분이 불가능하다. 결국 $x_0$는 임의의 점이 될 수 있어서 바이어슈트라스 함수 $W(x)$는 모든 점에서 미분이 불가능하다.

어떻게 상상하면 바이어슈트라스 함수를 쉽게 이해할 수 있을까? 이 함수는 모든 점에서 연속이기 때문에, $x$가 정해지면 $y$ = $W(x)$를 결정할 수 있다. 만약 2차원 평면에 점을 찍으면 곡선 $(x, y)$는 정확하게 결정된다. 하지만 점 $x$의 근방은 절대 결정할 수 없다. 주변이 무한대의 빠르기로 변하기 때문이다. 이런 곡선이 실제로 존재할 수 있을까? 점의 궤적은 정확히 존재하지만 모양이 부드럽지 않고 한없이 뾰족한 곡선이 있다. 바로 분수 차원(fractional dimension)을 가진 프랙탈(fractal) 도형이다.

[그림 3] 바이어슈트라스 함수의 자기 유사성(출처: wikipedia.org)

프랙탈이 강조하는 자기 유사성(self-similarity)을 이용해 [그림 3]처럼 바이어슈트라스 함수 $W(x)$를 관찰할 수도 있다. 자기 유사성은 식 (7)에 제시한 $W(x)$의 미분 불가능 증명에도 적극적으로 활용하고 있다. 자기 유사성을 증명하기 위해 원래보다 구간을 $1/b^m$만큼 줄여서 $W(x)$를 다시 써본다.

                  (18)

식 (18)에 의해 바이어슈트라스 함수 $W(x)$는 크기가 $a^m$만큼 작고 척도(scale)가 $1/b^m$만큼 줄어든 자신과 닮은 $W(u)$를 포함하고 있다. 이뿐만 아니라 자연수 $m$은 임의로 선택할 수 있어서 $W(x)$는 자기 유사성이 있는 함수를 무한개 가지고 있다.

[참고문헌]

[1] J. Thim, Continuous Nowhere Differentiable Functions, Master Thesis, Luleå University of Technology, Sweden, 2003.

[2] G. H. Hardy, "Weierstrass's non-differentiable function," Trans. Am. Math. Soc., vol. 17, no. 3, pp. 301–325, Jul. 1916.

[다음 읽을거리]

1. 분수 차원을 가진 프랙탈

연산 미적분학(Operational Calculus)

[경고] 아래 글을 읽지 않고 "연산 미적분학"을 보면 바보로 느껴질 수 있습니다.

1. 라플라스 변환

2. 라플라스 변환의 성질

3. 베타 함수

위대하지만 은둔형 물리학자인 헤비사이드Oliver Heaviside(1850–1925)의 피와 땀이 스민 물리학 이론이 맥스웰 방정식(Maxwell's equations)이라면, 수학 이론은 당연히 연산 미적분학(operational calculus)이다[1]–[3]. 연산 미적분학은 간단하게 연산자법(operational method)이라고도 한다. 연산 미적분학은 텐서 미적분학(tensor calculus)과 더불어 19세기 수학의 위대한 성취라고 한다[4]. 물리학자인 헤비사이드가 1893년헤비사이드 43세, 조선 고종 시절에 제안한 연산 미적분학에 수학자들이 이와 같은 찬사를 보내는 이유가 있다. 연산이라고 하면 수학적 계산이나 유도를 포함한 인간적 활동이다. 연산을 정의하는 연산자(operator)는 수학적 활동을 위한 표기법이나 도구일 뿐이다. 단순한 연산자에 새로운 대수적 의미를 부여해서 마치 숫자처럼 연산자를 자유자재로 다루는 미적분학 분야가 연산 미적분학이다. 연산 미적분학을 이용하면, 미분(differentiation)과 적분(integration) 개념을 우리 상상에 따라 한없이 넓게 확장할 수 있다.

헤비사이드가 만든 뛰어난 업적에 비해 물리학이나 수학 분야에서 헤비사이드의 이름을 찾기는 매우 어렵다. 겨우 남아있는 부분이 단위 계단 함수(unit step function)를 헤비사이드 계단 함수(Heaviside step function)로 부르는 정도이다. 하지만 헤비사이드가 남긴 유산은 엄청나다. 고등학교만 나온 헤비사이드는 박사들이 즐비한 과학계에서 독창성, 집요함, 단순함으로 경쟁했다. 맥스웰이 제안한 방정식에 있는 사원수(quaternion)라는 난해함을 제거하기 위해 기브스와 독립적으로 좌표계 기반 벡터(vector)를 맥스웰 방정식에 도입했다. 요즘 우리가 쓰는 맥스웰 방정식은 헤비사이드가 제안한 단순 형태이므로, 정확히 부르자면 맥스웰–헤비사이드 방정식(Maxwell–Heaviside equations)이라 함이 옳다. 헤비사이드는 복잡한 미분 방정식도 싫어해서 초보적인 대수적인 해법을 적극적으로 찾았다. 이런 접근법의 결과로 헤비사이드는 페이저(phasor), 교류 회로 해석법, 연산 미적분학[1], [2], 라플라스 변환(Laplace transform)[5], [6] 등을 제안하게 된다. 라플라스 변환만 해도 적분 형태는 오일러나 라플라스Pierre-Simon Laplace(1749–1827)가 먼저 제안했지만, 라플라스 변환 개념을 이용한 미분 방정식의 새로운 해법은 헤비사이드의 공이다. 그래서 라플라스 변환도 라플라스–헤비사이드 변환(Laplace–Heaviside transform)으로 불러야 한다.

연산 미적분학의 기본 전략은 매우 단순하다. 페이저(phasor)처럼 미분 방정식에 나오는 미분 연산자 $d/dt$를 대수적인 수 $p$로 바꾸고 $p$를 대수적으로 잘 정리해서 원래 미분 방정식의 해를 구한다. 이 개념은 라플라스 변환으로 미분 방정식의 해를 쉽게 구하는 방식과 매우 비슷하다. 예를 들어 라플라스 변환의 미적분 공식을 살펴보자.

                  (1)

                  (2)

여기서 $s$는 라플라스 변환에 나타나는 복소수(complex number)이다. 상식적으로 미분 연산자가 $s$라면, 적분 연산자는 미분의 역연산자라서 $1/s$이 되어야 한다. 식 (1)과 (2)에서 미적분에 대한 $s$의 거듭제곱 관계가 잘 성립하므로, 라플라스 변환은 연산 미적분학의 기본 철학을 완전하게 구현한다. 사실 수학적으로 불완전한 연산 미적분학을 복소 함수론(complex analysis)으로 엄밀하게 정의한 이론이 바로 라플라스 변환이다.

헤비사이드는 라플라스 변환에 나오는 복소수 $s$를 사용하지 않고 연산자를 대체한 수 $p$를 이용해 자신만의 이론을 정립했다. 예를 들어 어떤 함수 $F(t)$의 미분이 $f(t)$로 정해졌을 때, 연산 미적분학 관점에서 $F(t)$는 다음처럼 구해진다.

                  (3)

더욱 복잡한 경우에도 식 (3)과 같은 기호적 연산(symbolic operation)을 할 수 있다. 예를 들어 $f(t)$가 입력, $F(t)$는 시스템 응답일 때, 미분 방정식을 다음처럼 풀 수 있다.

                  (4)

헤비사이드는 식 (4)의 우변 분모에 있는 $p$에 대한 다항식을 분자로 올리기 위해 $1/p$에 대한 무한 급수로 전개했다. 분자에 생긴 무한 급수를 테일러 급수와 비교해서 미분 방정식의 답을 쉽게 구했다. 즉 연산 미적분학에서는 $f(t)$를 무한번 적분해서 시스템 응답 $F(t)$를 쉽게 구한다. 수학자들이 연산 미적분학을 공격한 지점이 바로 이곳이다. 무한 급수로 전개한 결과가 수렴한다는 보장을 어떻게 하는가? 그래서 헤비사이드의 연산 미적분학은 문제가 너무 많다고 지적했다.[헤비사이드는 총 3편의 연산 미적분학 논문을 준비했지만, 수렴과 발산 문제로 인해 3번째 논문은 게재 거절되었다.] 하지만 헤비사이드는 결과가 제대로 나오는 연산 미적분학을 포기할 생각이 없었다. 굳건하게 자신의 이론을 지켜내고 전자기학에도 성공적으로 적용했다. 헤비사이드와 수학자의 이견을 해결한 사람은 브롬위치Thomas John I'Anson Bromwich(1875–1929)이다[3]. 브롬위치는 연산 미적분학에 복소 함수론을 도입해서 헤비사이드 방법론의 수렴과 발산을 확실하게 구별할 수 있었다. 그래서 지금은 연산 미적분학이 거의 쓰이지 않고, 더 탄탄한 수학적 기반을 가진 라플라스 변환이 미분 방정식 해법의 대세가 되었다. 하지만 우리 상상력의 한계를 경험하고 싶다면 연산 미적분학도 적극적으로 이해하고 활용할 필요가 있다.

[그림 1] RL 전기 회로(출처: wikipedia.org)

연산 미적분학이 적용되는 원리를 파악하기 위해 [그림 1]에 제시한 RL 전기 회로를 계산한다. RL 회로의 입력 $v_\text{in}(t)$는 단위 계단 함수 $u(t)$로 가정한다. 교류에 대한 KVL(Kirchhoff voltage law)을 적용하면, [그림 1]에 흐르는 전류 $i(t)$는 다음과 같은 미분 방정식을 만족한다.

                  (5)

연산 미적분학 관점에서 식 (5)에 있는 미분 연산자 $d/dt$를 $p$로 바꾼 후, 대수적으로 계산해 $i(t)$를 구한다.

                  (6)

적분을 위해 식 (6)의 결과를 $1/p$에 대한 무한 급수로 전개한다.

                  (7)

식 (7)에 등장한 $1/p$의 대수적 거듭제곱은 다음에 정의할 다중 적분 연산으로 바꾸어 표기할 수 있다. 왜냐하면 $1/p$가 $p$의 역수인 것처럼 적분은 미분의 역연산이기 때문이다.

                  (8)

식 (8)은 낯익은 결과이다. 바로 테일러 급수(Taylor series)에 등장한 멱급수의 개별 항이다. 신기하게도 테일러 급수가 연산 미적분학과 밀접하게 연결되어 있다. 식 (8)을 식 (7)에 대입해서 다시 정리한다.

                  (9)

여기서 $t \ge 0$, $L/R$은 회로의 시정수(時定數, time constant, $\tau$)이다. 식 (9)는 식 (5)를 미분 방정식으로 풀어서 나온 해와 완전히 동일하다. 따라서 연산 미적분학은 미분 방정식을 대체하는 새로운 해법임이 분명하다. 다만 식 (7)의 마지막식을 만들 때, 무한 급수의 수렴을 고려하지 않았기 때문에 애매함이 있다. 이 부분은 수학자들이 헤비사이드의 연산 미적분학을 공격한 좋은 소재였다. 시간 $t$ = $0$에서 인덕터(inductor)에 초기 전류 $i(0)$이 있더라도 연산 미적분학을 다음처럼 사용할 수 있다.

                  (10)

식 (10)의 첫째식에 연산 미적분학을 적용할 때는 미분 처리에 주의해야 한다. 미분 연산에서는 당연히 $d[i(t) - i(0)]/dt $ = $di(t)/dt$이지만, 미분 연산을 대수 $p$로 바꾸면 $p[i(t) - i(0)]$ $\ne$ $p i(t)$이다. 그래서 $i(0)$에서 $i(t)$로의 변화를 나타내는 미분의 특성으로 인해, 미분은 대수적으로 $p[i(t) - i(0)]$로 표현되어야 한다. 이 관계를 라플라스 변환으로 보면 식 (1)의 첫째식과 동등하다. 연산 미적분학의 애매한 유도 과정은 라플라스 변환에서 세련되게 다음처럼 바뀐다.

                  (11)

여기서 $I(s)$는 $i(t)$의 라플라스 변환, $\Re[s] > 0$을 만족해야 한다. 연산 미적분학에서는 $1/p$에 대한 무한 급수의 수렴성을 판정하지 못했지만, 라플라스 변환은 $s$에 대한 유리 함수가 수렴하는 조건을 정확히 제시한다.

미분에 대한 인식을 확장해주는 연산 미적분학을 재미있는 적분인 길쌈(convolution)에도 적용해본다.

                  (12)

식 (12)에 있는 $g(t-\tau)$를 테일러 급수로 전개하고 미분 연산자 $d/dt$를 대수 $p$로 바꾸어본다.

                  (13)

식 (13)의 마지막식에 등장한 적분을 보면, 길쌈에는 내재적으로 라플라스 변환이 존재하고 있다. 하지만 라플라스 변환과 같은 형태이더라도 $e^{-p \tau}$는 엄연히 $g(t)$에 작용하는 미분 연산자이다. 대수 $p$를 그대로 두고 $t \to \infty$를 적용하면 식 (13)의 마지막식은 드디어 라플라스 변환이 된다. 여기서 $g(t)$의 점근값은 $u(t)$처럼 $1$이라 가정한다. 식 (13)을 이용한 라플라스 변환의 유도는 연산 미적분학의 자유로움과 한계를 명확히 보여준다. 연산자를 숫자처럼 대수 규칙에 따라 다루어서 다양한 공식을 유도할 수 있다. 하지만 본질적으로 $p$는 연산자이기 때문에, 우리가 얻은 결과가 엄밀한 수준에서 타당한지 잘 모른다. 이러한 난제는 $p$를 복소수 $s$라 생각해서 복소 함수론(complex analysis)을 적용하면 쉽게 해결된다.

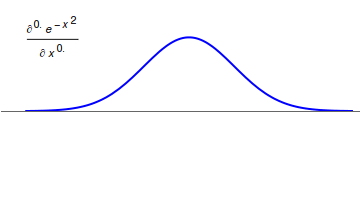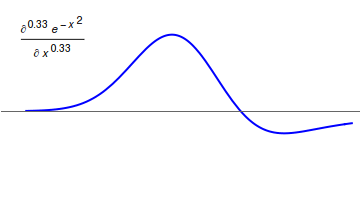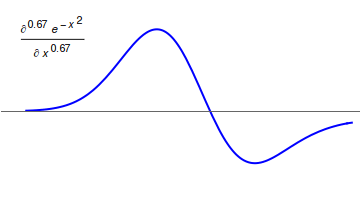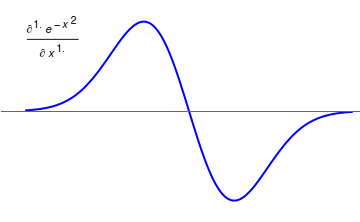
[그림 2] 가우스 함수의 분수 미분(출처: wikipedia.org)

연산 미적분학이 잘 적용될 수 있는 분야 중 하나가 분수 미적분(fractional differentiation and integration) 혹은 분수 미적분학(fractional calculus)이다. 미분이나 적분은 원래 연속적으로 한 번씩 할 수는 있어도 분수 번 할 수는 없다. 어떻게 미분과 적분을 정의하면 정수까지 포함해서 분수 번 연산을 적용할 수 있을까? 바로 연산 미적분학이 답이다. 예를 들어 거듭제곱 $x^m$을 $n$번 미분한 결과를 보자.

                  (14)

여기서 $m \ge n$이다. 미분 연산자 $d/dx$를 대수 $D_x$로 바꾸고 감마 함수(gamma function)를 이용해서 자연수 $m$과 $n$을 분수 $\mu$와 $\nu$로 각각 바꾸어쓴다.

                  (15a)

                  (15b)

식 (15a)에 기반을 두고 테일러 급수와 결합해서 일반적인 분수 미적분 공식을 얻는다.

[분수 미적분]

연산 회수 $\nu$가 양수이면 미분, $\nu$가 음수이면 적분이 된다.

                  (16)

여기서 $f(x)$는 구간 $[0, x]$에서 연속(continuity), $\lim_{t \to x} (x-t)^{-\nu} f(t)$ = $0$이 성립한다.

[증명]

함수 $f(x)$를 $x$ = $0$에서 테일러 급수로 전개해서 식 (15a)를 적용한다.

                  (17)

여기서 $f^{(m)}(x)$는 $f(x)$에 대한 $m$번 미분이다. 식 (17)의 결과에 베타 함수(beta function)를 적용해서 다시 정리한다.

                  (18)

또한 식 (16)에 부분 적분을 적용해서 $(x-t)^{-\nu-1}$의 차수를 높인다.

                  (19)

식 (19)의 적분이 존재하려면, 극한은 $\lim_{t \to x} (x-t)^{-\nu} f(t)$ = $0$이 되어야 한다.

______________________________

식 (16)처럼 정의하는 적분은 리만–리우빌 적분(Riemann–Liouville integral)이라 부른다. 만약 $\nu > 0$인 경우는 $\lim_{t \to x} (x-t)^{-\nu} f(t)$ = $0$인 조건을 만족할 수 없다. 이때는 식 (1.2)를 이용하여 다음처럼 분수 미분이 아닌 분수 적분을 한다.

                  (20)

여기서 $n$ = $\lceil \nu \rceil$, $\lceil x \rceil$는 천장 함수(ceiling function)이다. 식 (16)에 정의한 분수 미적분은 연산처럼 보이지만 사실은 적분 변환이다. 분수 미분 회수 $\nu$가 정수인 경우에만 이 적분 변환은 통상적인 미분이나 적분이 된다. 또한 식 (16)은 라플라스 변환의 길쌈(convolution)인 식 (12)와도 매우 유사하다. 그래서 분수 미적분을 다음과 같은 라플라스 변환과 역변환으로 정의할 수도 있다.

                  (21)

[그림 3] 지수 함수의 분수 미분을 위한 닫힌 경로

미분과 적분의 항등원인 지수 함수(exponential function) $e^{at}$에 대한 분수 미분을 해보자. 식 (16)에 대입해서 계산하면 좋겠지만, 베타 함수의 피적분 함수가 곱해 있어서 적분이 쉽지 않다. 이 경우는 식 (21)이 더 유리하다. 함수 $f(t)$ = $e^{at}$의 라플라스 변환 $F(s)$ = $\frac{1}{s-a}$를 대입해서 정리한다.

                  (22)

여기서 $\Re[s] > a$, 자연수가 아닌 실수 $\nu$는 $\nu > 0$이다. 시간 $t$가 $0$보다 크고 $s^\nu$에 대한 가지 자름(branch cut)을 음의 실수축으로 정하면, 유수 정리(residue theorem)를 적용하기 위한 닫힌 경로는 [그림 3]과 같다. 따라서 [그림 3]과 유수 정리에 따라 지수 함수에 대한 새로운 분수 미분을 다음처럼 얻는다.

                  (23)

미분 회수 $\nu$가 자연수라면, 당연히 지수 함수는 미분의 항등원이 된다. 하지만 자연수가 아닌 실수 $\nu$로 인해 분수 미분에는 복잡한 적분 항이 추가로 더 붙는다. 그래서 분수 미분은 일종의 새로운 적분 변환으로 간주할 수 있다.

   1. 기본(basics)   

식 (15a)와 (16)을 이용하면 다양한 분수 미적분 공식을 쉽게 증명할 수 있다.

[미분 법칙]

                  (1.1)

                  (1.2)

[증명]

식 (16)을 증명할 때 테일러 급수를 이용하므로, 식 (15a)를 다음처럼 변형한다.

                  (1.3)

따라서 식 (1.2)가 성립한다.

______________________________

[참고문헌]

[1] O. Heaviside, "On operators in physical mathematics, Part I," Proc. Roy. Soc. Lond., vol. 52, pp. 504–529, Jan. 1893.

[2] O. Heaviside, "On operators in physical mathematics, Part II," Proc. Roy. Soc. Lond., vol. 54, pp. 105–143, Jan. 1894.

[3] H. Jeffreys, "Bromwich's work on operational methods," J. London Math. Soc., vol. 3,  220–223, Jul. 1930.

[4] R. Watson-Watt, “Oliver Heaviside: 1850–1925,” The Scientific Monthly, vol. 71, no. 6, pp. 353–358, 1950.

[5] J. R. Carson, "The Heaviside operational calculus," Bull. Amer. Math. Soc., vol. 32, no. 1, pp. 43–68, Jan.–Feb. 1926.

[6] J. Staines, The Heaviside Operational Calculus: The Laplace Transform for Electrical Engineers, 2nd ed., CreateSpace Independent Publishing Platform, 2013.

[다음 읽을거리]

1. 아벨의 적분 방정식