1. 푸리에 급수의 시작
2. 디랙 델타 함수
3. 복소 함수론의 이해
[푸리에 변환 소개]
수학 분야에서 푸리에 급수(Fourier series)는 아주 성공적이지만, 푸리에 변환(Fourier transform)은 기법의 폭발력에서 푸리에 급수를 훨씬 넘어선다. 현대 통신의 시작과 끝이 푸리에 변환이기 때문에 통신 전분야에서 광범위하게 쓰이는 개념이 푸리에 변환이다. 청출어람(靑出於藍)이란 말에 딱 맞는 경우가 바로 푸리에 변환이다.

[그림 1] 통신의 개념(출처: wikipedia.org)
푸리에 변환은 푸리에 급수의 약점을 보완하기 위해 제안된 적분 변환(integral transform)이다. 이름에서도 알 수 있듯이 최초 제안자는 푸리에Joseph Fourier(1768–1830)이다. 식 (1)의 푸리에 급수는 유용하지만 함수가 반드시 주기적이어야 한다는 제약 조건이 있다.
 (1)
(1)
이 문제를 해결하는 방법은 주기($T$)를 무한대로 보내기이다. 그러면 비주기 함수도 푸리에 급수로 변환할 수 있다. 다만 주기를 무한대로 보낸 경우는 푸리에 급수라 하지 않고 푸리에 적분(Fourier integral) 혹은 푸리에 변환(Fourier transform)이라 한다. 푸리에 적분과 푸리에 변환은 같은 공식을 다른 관점에서 표현한 적분이다. 푸리에 급수의 주기를 늘려서 급수를 적분 형태로 만들면 푸리에 적분이라 한다. 푸리에 변환은 시간 함수를 주파수 함수로 바꾸어 생각한다. 즉 푸리에 적분과 푸리에 변환은 설명이 약간 다르지만 같은 수식의 서로 다른 이름이다.
식 (1)을 이용해 푸리에 적분 혹은 푸리에 변환을 정의한다. 먼저 식 (1)에서 $F_m \cdot T$를 만들고 주기 $T$를 무한대로 보낸다. 그러면 새로운 변수 $F(\omega)$는 다음처럼 정의된다.
 (2a)
(2a)
여기서 $m$은 식 (1)의 푸리에 급수를 표현하고 있으므로 먼저 무한대로 가야 한다. 이런 푸리에 급수 조건을 만족시킨 후, 그 다음에 $T$를 무한대로 보낸다. 시간 범위 $T$가 유한한 경우 정의되는 $F_T(\omega)$ = $F_m \cdot T$는 절단된 푸리에 변환(truncated Fourier transform)이라 명한다. 절단된 푸리에 변환은 모든 시간을 관측하기 어려워 특정 시간 동안만 관찰해서 만드는 근사적인 푸리에 변환이다.
 (2b)
(2b)이산적인 $m \cdot \omega_0$가 연속적인 $\omega$가 되는 이유를 알려면 적분(integration)의 의미를 봐야 한다. 단순하게 생각하면 $\omega_0$는 이산적인 각주파수(angular frequency)의 간격이므로 주기 $T$가 커질수록 $\omega_0$는 $2 \pi /T$에 의해 작아진다. 그러면 주기 $T$가 커짐에 따라 각주파수 간격 $\omega_0$는 계속 줄어들어 이산적인 값이 연속적인 값으로 바뀌는 모습을 상상할 수 있다. 또한 $m$은 무한대로 발산하고 있으므로 각주파수가 변할 수 있는 범위는 $-\infty$에서 $\infty$임을 알 수 있다.
식 (2)의 개념과 이산적 각주파수의 특성을 식 (1)의 첫째식에 도입하면 함수 $f(t)$를 푸리에 변환 $F(\omega)$로 표현할 수 있다.
 (3)
(3)
식 (3)의 유도 과정을 정확히 이해하려면 적분법(integration)을 반드시 이해해야 한다. 추가로 식 (3)은 푸리에 변환의 매우 중요한 특징이다. 원래 함수 $f(t)$와 그 푸리에 변환 $F(\omega)$가 일대일 대응(一對一對應, one-to-one mapping)함을 보여준다. 만약 서로 다른 함수 $f_1(t)$와 $f_2(t)$가 동일한 푸리에 변환 $F(\omega)$를 가진다면 어떻게 될까? 푸리에 역변환(inverse Fourier transform)을 의미하는 식 (3)에 의해 $f_1(t) = f_2(t)$가 반드시 성립해야 한다. 즉, 푸리에 변환 $F(\omega)$가 같으면 변환의 원래 함수 $f(t)$는 유일하다. 식 (2)를 식 (3)에 대입하면 재미있는 관계 하나를 유도할 수 있다.
 (4)
(4)
식 (4)는 모든 $t$에 대해 성립하므로 디랙 델타 함수(Dirac delta function)를 쓰면 다음처럼 멋진 적분식이 증명된다.
 (5)
(5)
식 (5)는 복소 함수론(complex analysis or complex function theory)을 이용해서도 증명 가능하다.

[그림 2] 복소 적분을 위한 닫힌 경로(출처: wikipedia.org)
[푸리에 변환과 디랙 델타 함수]
 (6)
(6)[증명: 복소 함수론]
복소 지수 함수 $e^{i \omega |t - t'|}$은 적분이 잘 되지만, 식 (6)처럼 적분 구간이 무한하면 정적분이 정의되지 않는다. 이를 해결하기 위해 해석 함수를 다루는 복소 함수론을 적극적으로 활용한다. 적분 변수 $\omega$에 대해 $e^{i \omega |t - t'|}$은 해석적이어서 복소 평면 상에 어떤 적분 경로를 잡더라도 적분이 가능하고 유수(residue)도 없다. 먼저 $t > t'$인 경우로 가정해서 식 (6)의 우변을 계산한다. 식 (6)의 우변을 있는 그대로 적분하기는 어려우므로[∵ 함수 $e^{i \omega |t - t'|}$를 제외한 나머지 부분이 상수이기 때문에], 시간 $t$에 대해 식 (6)을 다시 적분한다.
 (7)
(7)여기서 $\Delta > 0$, $T > 0$, $T > \Delta$이다. 식 (7)의 둘째 줄에서 적분 순서를 바꿀 수 있는 이유는 조르당의 보조 정리(Jordan's lemma)에 의해 $\omega$에 대한 적분[= $\int_{-\infty}^\infty e^{i \omega (t-t')}\,d\omega$]의 절대값이 $\pi \mathbin{/} |t - t'|$보다 작은 성질에 기인한다. 식 (7)과 같은 접근법은 디랙 델타 함수의 정의에 쓰는 슈바르츠Laurent Schwartz(1915–2002)가 제안한 분포(distribution)에 해당한다. 분포 관점에서는 함수를 그대로 두지 않고 정적분해서 그 결과를 관찰한다. 구간 선택에 관계없이 정적분된 결과가 하나로 고정되면, 이 함수는 디랙 델타 함수의 성질을 가진다.
다음 단계로 식 (7)의 마지막 적분 구간을 전체 실수에서 [그림 2]처럼 닫힌 복소 경로로 바꾼다. 이 절차는 [그림 2]에 있는 $c_1$을 따라가는 적분이 조르당의 보조 정리로 $0$이 되는 결과를 이용한다. 새로운 닫힌 경로 $c_1 + c_2$ 내부에 극점(pole)이 없어서 유수는 없으므로, 유수 정리(residue theorem)에 따라 [그림 2]의 닫힌 경로 적분은 $0$이 된다. 그래서 식 (7)의 적분도 $0$이 된다.
 (8)
(8) (9)
(9)쉽게 생각해서 피적분 함수가 0이면 적분도 0이다. 하지만 적분이 0이라고 해서 피적분 함수가 0이 될 필요는 없다. 하지만 식 (9)의 관계가 성립하는 적분은 피적분 함수가 반드시 0이어야 하기 때문에[적분 구간을 계속 바꾸어도 적분이 항상 0이라면 피적분 함수가 꼭 0이어야 하므로], 식 (7)의 피적분 함수는 당연히 0으로 나온다. 시간이 $t < t'$인 경우도 식 (7)–(9)와 비슷한 과정을 거쳐서 적분값이 $0$임을 확인한다. 다음 단계로 $t$ $\approx$ $t'$ 근방에서 식 (6)의 우변을 적분한다.
 (10)
(10)여기서 $\Delta$는 임의로 작게 잡을 수 있다. 식 (10)의 둘째 줄에 있는 피적분 함수에는 $e^{-i \omega \Delta}$가 있기 때문에, $c_1$에서 적분이 발산해서 전체 실수에 대한 적분을 [그림 2]와 같은 경로로 바꿀 수 없다.[즉, 그림 2의 큰 반원에서 $e^{-i \omega \Delta}$가 발산한다.] 그래서 $\omega$의 부호를 바꾸어서 [그림 2]의 $c_1$ 경로에서 발산하지 않게 한다.[$\omega \to -u$] 또한 식 (10)의 마지막 과정은 손쉽게 유수 정리(留數定理, residue theorem)를 이용할 수도 있다.

[그림 3] 양뱡향으로 감쇠하는 지수 함수
[증명: 로렌츠–코쉬 함수(Lorentz–Cauchy function)]
 (11)
(11)
여기서 $\sigma$는 임의의 작은 양의 실수이다. 식 (11)에서 $\sigma \to 0$일 때, 성급하게 푸리에 변환값을 $0$이라고 하면 안된다. 대부분은 $0$이 되지만 $\omega$까지 $0$이 되면 분모가 $0$이 되는 문제가 생긴다. 아래에 제시한 디랙 델타 함수를 만드는 로렌츠–코쉬 함수(Lorentz–Cauchy function)를 고려한다.
식 (6)의 우변을 정적분하기 위해, [그림 3]처럼 양방향으로 감쇠하는 지수 함수의 푸리에 변환을 구한다.
 (11)
(11) (12)
(12) (13)
(13)
식 (2)처럼 푸리에 급수로부터 푸리에 변환을 유도함이 일반적이지만 푸리에 변환으로부터 푸리에 급수를 유도할 수도 있다. $f(t)$가 주기 함수(periodic function)인 경우도 식 (2)를 이용해 푸리에 변환을 구할 수 있다. 즉, 주기 함수도 함수이므로 푸리에 변환식에 넣어 아래와 같이 적분을 해본다.
 (14)
(14)
그러면 식 (14)처럼 한 주기에 대한 적분과 무한 급수(infinite series)의 곱으로 이루어진 결과를 얻을 수 있다. 더 진행하기 위해 충격 열(impulse train)에 대한 다음 관계를 이용한다.
 (15)
(15)
식 (15)에 의해 식 (14)에 있는 무한 급수는 디랙 델타 함수로 표현될 수 있다. 식 (15)를 식 (14)에 대입하여 정리하면 다음 푸리에 급수를 얻을 수 있다.
 (16)
(16)여기서 $\omega_0$ = $2 \pi/T$이다. 식 (16)에 의해 주기 함수의 푸리에 변환 $F(\omega)$은 충격 열(impulse train)로 표현된다. 충격 열에 있는 각 디랙 델타 함수의 크기는 푸리에 계수 $F_m$이다. 식 (16)에서 주기 함수의 푸리에 변환이 발산하는 이유는 푸리에 변환의 적분 구간인 음의 무한대에서 양의 무한대까지 함수값이 계속 존재하기 때문이다.[∵ 주기 함수의 정의에 의해 모든 시간에서 함수가 주기적으로 존재해야 한다.]
식 (2)와 (3)을 종합하여 다음의 푸리에 변환쌍(Fourier transform pair)을 정의할 수 있다.
 (17)
(17)
푸리에 변환쌍은 서로 일대일 대응이 되므로 시간 영역 $f(t)$를 풀든지, 주파수 영역 $F(\omega)$를 풀든지 동일한 결과를 얻는다. 이건 굉장히 중요한 관점을 보여준다. 시간 함수 $f(t)$로 특성 해석이 어려운 경우 다른 영역인 $F(\omega)$를 고려하면 시간 함수 $f(t)$의 특성을 쉽게 얻을 수도 있다. 물론 이건 그때 그때 다르다.
푸리에 변환이 내포하고 있는 특성을 좀더 고민한다. 식 (3)의 최종 결과를 보면 푸리에 변환은 다음과 같다.
 (18)
(18)
식 (18)의 좌변은 우리가 흔히 보는 시간 영역(time domain) 신호이다. 시간 영역 신호는 [그림 4]처럼 시간에 따라 진폭이 변화되는 신호이다.

[그림 4] 시간 영역 신호의 파형(출처: wikipedia.org)
우리가 신호의 특성을 관측하는 방법 중의 하나는 시간에 대해 진폭 특성이 어떻게 변하는 가를 관찰하기이다. 즉, 특정 지점의 진폭 관측하기는 시간 영역의 관측법이다. 식 (18)의 우변은 시간 영역 관측과는 전혀 다르게 빈도수[혹은 주파수]의 분포를 구해 이 빈도수 분포를 무한히 합친다. [그림 5]처럼 시간에 따라 주기적으로 변하는 신호들을 분포[혹은 주파수별 진폭]에 맞게 모으면 신기하게도 시간 영역 관측과 일치한다는 개념이 푸리에 변환의 의미이다.
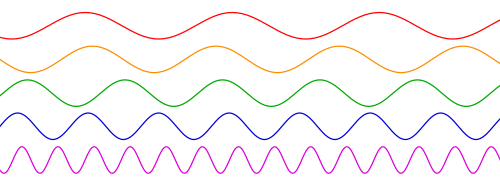
[그림 5] 주파수가 일정한 신호들(출처: wikipedia.org)
이 성질은 상식적으로 이해할 수 없는 결과이다. 하지만 식 (18)의 좌변과 우변이 같다는 증명은 이미 식 (3)에 나와있다. 이 부분이 푸리에 변환을 처음 배울 때 헷갈리는 점이다. 초보자 눈에는 함수를 표현할 때 식 (18)의 우변처럼 $f(t)$로 쓰면 쉬울 것 같다. 하지만 [그림 4]를 다시 본다. 실제 시간 영역 파형은 시간적으로 복잡하며 더군다나 계속 변하고 있다. 예를 들어, [그림 4]의 파형을 수학 함수로 표현본다. 잘 할 수 있는가? [그림 4]와 같은 파형을 수학적으로 효과적이게 표현하려면 빈도수[혹은 주파수]를 기준으로 함수를 표현하면 된다. 시간적으로 변하는 성분은 잘 알려진 지수 함수(exponential function) $\exp(i \omega t)$로 표현하고 주파수별 진폭[실제로는 복소수]에 해당하는 $F(\omega)$에만 집중하면 [그림 4]의 시간 파형을 [그림 5]와 같은 주기 함수의 무한 합으로 표현할 수 있다. 주파수별 진폭을 표현하는 공간은 주파수 영역(frequency domain)이라 한다. 다른 관점으로 보면 식 (18)의 좌변에 표시한 함수 $f(t)$는 시간 $t$와 어떤 함수 관계를 가지고 있는지 전혀 알 수 없다.[∵ 함수 이름이 $f(t)$라는 부분 외에 아무런 정보도 없다.] 하지만 식 (18)의 우변을 보라. 이 함수 $f(t)$는 시간 변화가 분명히 $\exp(i \omega t)$에 연관되어 있다. 믿을 수 없지만 임의의 모든 함수 $f(t)$가 $\exp(i \omega t)$에 연관되어 있다.
[그림 6] 천지창조(출처: wikipedia.org): 벽화의 3차원 영상은 [여기]
계속 강조하고 있는 푸리에 변환의 핵심은 현재 시간 $t$와 전혀 관계없는 새로운 영역인 빈도수 $f$로 해석 관점을 바꾸기이다. 현재 시점에 집중하지 않고[시간 영역] 신의 영역에 해당하는 태초부터 세상 끝까지 퍼져 있는 주기 함수[혹은 빈도수]의 분포[주파수 영역]를 본다. 따라서, 현재를 관찰하지 말고 처음부터 끝까지 나타나는 빈도를 봄이 푸리에 변환이다. 푸리에 변환이 시간에 대해 적용되면 시간-주파수가 서로 쌍이 된다. 시간에 대한 봄과 주파수의 분포에 대해 봄은 서로 동일하다. 공간의 경우에는 공간과 파수(wavenumber)가 서로의 쌍이다. 즉, 공간에 집중하지 않고 공간적 주기의 빈도수 분포를 본다. 푸리에 변환은 시간과 공간에만 적용되지는 않는다. 현재 상태($t$)와 빈도수($\omega$)를 정의할 수 있는 어떤 곳에도 쓰일 수 있다. 식 (18)은 말 그대로 수학적 관계이므로 $t$-$\omega$ 대신 다른 변수를 써도 문제없다. 예를 들면 푸리에 변환은 사진 압축에도 쓰일 수 있다. 대표적인 압축 형태인 JPEG(Joint Photographic Experts Group)는 푸리에 변환의 일종인 이산 코사인 변환(discrete cosine transform, DCF) 기반하고 있다.

[그림 7] JPEG의 기저 함수(출처: wikipedia.org)
JPEG에서는 [그림 8]과 같은 사진을 있는 그대로 저장하지 않고 영상 처리(image processing)를 통해 [그림 7]과 같은 빈도수를 가진 기저 함수(basis function)의 진폭으로 저장한다. 즉, 영상 처리를 위해 JPEG는 사진을 8×8 픽셀(pixel) 단위로 쪼갠다. 8×8 픽셀은 하나의 블록(block)이 된다. HDTV의 기준 해상도인 1024×768 픽셀은 JPEG 블록 기준으로는 128×96 블록이 된다. 블록이 상하좌우로 변할 수 있는 빈도의 특성은 DCT를 따르므로 푸리에 급수(Fourier series)를 구성하는 기저 함수는 [그림 7]처럼 생겨야 한다. 이 기저 함수는 푸리에 급수의 삼각 함수 역할을 하므로, 우리가 결정할 부분은 삼각 함수의 계수이다. 즉 계산한 삼각 함수의 계수는 [그림 8]을 복원할 [그림 7]에 있는 기저 함수의 진폭으로 쓰인다. 이 진폭을 적당히 압축하면 저장되는 그림 파일의 크기를 획기적으로 줄일 수 있다.

[그림 8] 영상 처리의 시험 사진: 레나(출처: lenna.org)
영상 처리에 빈번하게 사용하는 사진은 [그림 8]의 레나(lena or lenna)이다[1]. [그림 8]처럼 레나는 영상 처리를 위한 다양한 시각적 요소들(곡선, 평면, 거울, 그림자, 살색, 질감 등)을 가지고 있으며 더군다나 대상이 아름다운 여인(?)이다[1]. 역사를 추적해 보면 '레나'는 원래 도색 잡지인 플레이보이(Playboy)에 나오는 사진이었다. 1970년 즈음 이를 불법으로 복사해서 영상 처리에 몰래 사용했고 용기 있는 누군가가 학술지에 영상 처리 이론과 함께 이 사진을 공개해서 사진이 급속도로 퍼졌다. 이후에 이 사진은 레나라는 이름도 가지게 되었고 사진의 주인공은 인터넷의 으뜸 여인 혹은 영부인(First Lady of the Internet)이 된다. 그래서 [그림 8]은 원래 상업적 사진이었으나 워낙 많이 사용되었기 때문에 저작권이 희미해진 사진 중의 하나이다.
푸리에 변환쌍은 식 (17)이 기본이기는 하지만, 푸리에 변환과 역변환의 정의가 $1/(2\pi)$만큼 다르다. 그래서 식 (17)의 둘째 정의에서 적분 변수를 $\omega$에서 $2 \pi f$로 바꾸어서 대칭적인 푸리에 변환쌍을 정의할 수 있다.
 (19)
(19)여기서 $df$ = $d\omega/(2 \pi)$이다. 그러면 주파수 영역의 변수만 $\omega$에서 $f$로 바뀔 뿐, 푸리에 변환된 결과는 $\hat g(f)$ = $F(\omega)$로 동일하다. 변수를 바꾸기 싫을 때는 상수 항 $1/(2\pi)$을 푸리에 변환과 역변환에 동등하게 나누면 된다.
 (20)
(20)식 (17)과 비교하면, $F(\omega)$ = $\sqrt{2 \pi} \hat F(\omega)$이어서 기준 변환과 상수배만큼 차이가 난다. 푸리에 변환쌍의 정의가 여러 개일 수 있어서, 관련 자료를 볼 때는 주의를 기울여야 한다. 약간 귀찮고 혼란스러운 느낌이 있지만, 푸리에 변환이 워낙 유명하고 많이 쓰이기 때문에 이런 번잡함이 생긴다. 그래서 푸리에 변환쌍에 대한 여러 정의도 잘 공부해둔다. 앞서간 선배 연구자의 어깨 위에 굳세게 서서 나만의 새로운 응용을 멋지게 만들 수 있을 것이다.
푸리에 변환은 여러 변수를 함께 쓸 수 있어서 다차원으로 쉽게 확장된다. 푸리에 변환쌍인 식 (7)이 여러 변수에 대해 곱해진다고 생각한다. 만약 $n$차원 위치 벡터(position vector)를 $\bar x$ = $(x_1, x_2, \cdots, x_n)$로 두면, 파수 벡터(wavenumber vector) $\bar k$ = $(k_1, k_2, \cdots, k_n)$에 대해 다차원 푸리에 변환(multidimensional Fourier transform) $\mathfrak{F}_n[\cdot]$과 역변환 $\mathfrak{F}_n^{-1}[\cdot]$은 다음과 같이 공식화된다[2].
 (21)
(21)여기서 벡터 내적(inner product)은 $\bar k \cdot \bar x$ = $k_1 x_1 + k_2 x_2 + \cdots + k_n x_n$이다.
[참고문헌]
[1] L.-M. Po, "Lenna 97: A complete story of Lenna," City University of Hong Kong, Hong Kong, 2001.
[2] E. M. Stein and G. Weiss, Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, 1971.
[3] 박원우, 딥러닝을 위한 푸리에 영상처리, 홍릉, 2023.
[다음 읽을거리]
1. 평면파를 이용한 푸리에 변환 기법
2. 한켈 변환












 (8)
(8)











 (20)
(20) (21)
(21)

 (24)
(24)




 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7)
 (1.8)
(1.8)

