1. 발산의 의미
18–19세기 과학과 수학을 주도했던 프랑스의 힘은 과학기술에 대한 전국민적 관심과 지도층의 적극적 지원에 있었다. 그 당시 프랑스의 힘을 보여주는 전형적인 인물이 푸리에Joseph Fourier(1768–1830)[1]이다.
[그림 1] 나폴레옹 황제의 대관식(출처: wikipedia.org)
재봉사의 아들로 태어난 푸리에는 9살과 10살에 어머니와 아버지를 차례로 잃었다. 비천한 신분에 부모의 도움조차 받을 수 없는 푸리에였지만 천주교에서 운영하는 학교에서 기초적인 교육을 받을 수 있었다. 라틴어와 프랑스어를 시작으로 학문적 재능을 보인 푸리에는 12살에 오세르 왕립군사학교(École Royale Militaire of Auxerre)에 입학했다. 처음에는 문학 분야에서 두각을 나타냈으나 곧 수학에 특출한 능력을 보였다. 20세 무렵에는 방황도 많이 했다. 천주교 사제가 되고 싶기도 하고, 수학 분야에 위대한 기여를 하고 싶기도 했다. 하지만 보통의 젊은이들처럼 자기 능력에 대한 확신이 없었다. 하지만 프랑스 전반에 스며들어 있던 수학적 환경과 당대 최고 수준의 전문가 집단이 있었기 때문에, 푸리에는 수학 분야 논문을 꾸준히 읽을 수 있었고 드물게 논문도 발표할 수 있었다. 25세때에는 프랑스 대혁명에도 적극적으로 참여하게 된다. 푸리에는 달변 능력을 가졌으며 사교성과 정치 성향도 굉장히 강했다. 강한 개성으로 인해 한 때 오해를 받아 혁명의 단두대에서 목이 잘린 뻔하기도 했지만, 운명은 푸리에에게 가혹하지 않았다[2]. 당시 명강사로 이름이 높았던 푸리에는 1795년푸리에 27세, 조선 정조 시절에 고등사범학교(École Normale Supérieure)에 들어가게 되었다. 여기서 라그랑주Joseph-Louis Lagrange(1736–1813), 라플라스Pierre-Simon Laplace(1749–1827)와 같은 위대한 스승들을 만났다. 푸리에의 능력이 특출났기 때문에, 라그랑주, 라플라스도 푸리에를 눈여겨 보게 되고 이후 서로 돈독한 관계를 계속 유지하게 된다. 하지만 푸리에가 후일 기여하게 되는 열 방정식(heat equation)과 푸리에 급수(Fourier series)[1]–[5]가 출현하기 위해서는 몇 가지 고난을 더 겪어야 했다. 과학자, 수학자, 정치가, 웅변가 등의 면모를 가진 푸리에를 유능한 나폴레옹이 그냥 둘 리가 없었다. 나폴레옹과 함께 한 이집트 원정에서 사막의 뜨거움을 느끼고 1801년푸리에 33세, 조선 순조 시절에 패퇴한 프랑스군과 함께 파리로 돌아왔다. 푸리에는 이집트 원정전에 근무하던 이공과대학(École Polytechnique) 교수로 남기를 원했지만, 나폴레옹은 그레노블(Grenoble) 도지사로 발령을 냈다. 푸리에는 도지사 업무를 수행하면서 틈틈이 남는 시간을 활용해 1802년부터 열 확산 문제를 본격적으로 풀게 된다. 드디어 만족할 만한 결과를 얻은 푸리에는 1807년 12월 21일에 열 방정식과 푸리에 해석법을 최초로 소개한 논문을 과학학술원(Académie des Sciences, French Academy of Sciences)에 제출했다. 하지만 결과는 다소 비참했다. 심사 위원을 맡은 푸리에의 박사 학위 지도교수 라그랑주와 대(大)수학자 라플라스는 푸리에 논문의 약점을 정확히 지적했다. 삼각 함수 급수가 수렴한다는 증명이 없었으며, 삼각 함수 급수(trigonometric series) 그 자체도 이미 1752년베르누이 52세, 조선 영조 시절에 다니엘 베르누이Daniel Bernoulli(1700–1782)가 편미분 방정식(partial differential equation)을 풀기 위해 사용했었다. 하지만 이런 수학적 약점이 있었지만, 푸리에의 방법론은 우아했으며 물리적으로도 타당해 보였다.
사실 푸리에가 1807년에 열 방정식과 그 해법을 제출한 이유는 과학학술원이 고체 속의 열 확산(heat diffusion in solids) 문제를 경진대회 주제로 삼아 1811년푸리에 43세, 조선 순조 시절에 수학상을 줄 예정이었기 때문이다. 순수 수학 관점의 논란이 있었지만, 푸리에보다 더 나은 해법을 제시한 사람이 없어서 1811년 수학상은 결국 푸리에에게 돌아갔다. 하지만 논란은 계속되어 과학학술원은 푸리에의 논문을 공식적으로 출판하지 않았다. 심사 위원 설득을 위해 푸리에는 자신의 급수가 수렴함을 수학적으로 증명했지만, 여전히 엄밀성이 떨어져 라그랑주는 푸리에의 방법론을 끝까지 불신했다. 아쉽게도 라그랑주가 원하는 수준의 세밀한 수학적 증명은 푸리에의 제자인 디리클레Peter Gustav Lejeune Dirichlet(1805–1859)의 몫이었다[5]. 이런 상황 때문에 푸리에는 독자적으로 열 방정식과 푸리에 급수를 계속 연구하였다. 드디어 1822년푸리에 54세, 조선 순조 시절에 자비로 책을 출판해서 푸리에 급수를 대중에게 공개할 수 있었다[3]. 수학계에는 푸리에 급수에 대한 의심이 계속 남아있었지만, 푸리에의 발상은 과학 전분야로 빠르게 퍼져나갔다. 푸리에는 상상도 못했겠지만, 열 문제를 풀기 위한 푸리에 급수는 약 50년 후 전자파 방정식을 풀기 위한 표준 방법론이 되었고, 약 100년 후에는 무선 통신 이론을 위한 기본 도구가 되었다.
그러면 푸리에가 만든 열 방정식(heat equation)을 유도한다. 1800년대 초반에는 열에 대한 두 가지 가설이 존재했다. 열은 어떤 유체의 흐름이라는 가설과 열은 입자의 운동이 만든다는 가설이 서로 경쟁했었다. 지금은 열이 유체가 아니고 운동 특성임을 확실히 안다. 그래서 푸리에는 안전하게 다음처럼 가정했다.
 (1)
(1)
여기서
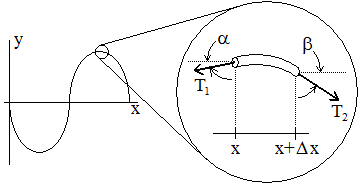
식 (1)을 잘 이해하려면 구배 연산자(gradient operator)
[표 1] 물질별 열 전도도(출처: wikipedia.org)
| 물질 (Substance) | 열 전도도 (W/K/m) (Thermal conductivity) | 측정 온도 (℃) (Temperature) |
기타 사항 (Other details) |
|---|---|---|---|
| 공기 | 0.026 | 25 | - |
| 스티로폼(styrofoam) | 0.033–0.04 | 25 | 폴리스티렌 폼 |
| 폴리프로필렌(polypropylene, PP) | 0.1–0.3 | 26 | - |
| 폴리스티렌(polystyrene, PS) | 0.12 | - | [6] |
| 테플론(Teflon, PTFE) | 0.25 | 20 | - |
| 물 | 0.6089 | 26.85 | - |
| 콘크리트(concrete) | 0.92 | - | - |
| 페라이트(ferrite) | 3.5–4.3 | - | - |
| 자석(magnet) | 9–12 | - | - |
| 알루미늄(aluminum) | 237 | 20 | - |
| 금(gold) | 315 | 26.85 | - |
| 구리(copper) | 384.1 | 18.05 | - |
| 은(silver) | 427 | 26.85 | - |
| 다이아몬드(diamond) | 895–1350 | 26.85 | - |
온도 차이가 생기면 열 흐름은 반드시 생기므로 식 (1)은 실험적으로 타당한 식이다. 식 (1)의 좋은 점은 열이 무엇인지와는 관계없이 나타나는 자연 현상을 수학적으로 표현했기 때문에 1800년대 당시에는 최선의 선택이었다. 열류(heat flow)[단위: W]
 (2)
(2) (3)
(3)
여기서

[그림 3] 체적과 표면적의 방향 정의(출처: wikipedia.org)
식 (3)의 표면 적분(surface integral)을 이해하기 위해 [그림 3]의 표면적 방향을 본다. 표면적 벡터는 항상 내부에서 외부로 나오는 방향으로 정의한다. 그래서 식 (3)의 열류 밀도
 (4)
(4)
즉, 열 용량
 (5)
(5)
식 (5) 유도에는 발산 정리(divergence theorem)를 적용한다. 식 (5)의 첫째식처럼 체적 적분으로 만들기 위해 열 용량
 (6)
(6)
여기서
[표 2] 물질별 등압(isobaric) 비열 용량(출처: wikipedia.org)
| 물질 (Substance) | 비열 용량 (J/K/kg) (Specific heat capacity) | 측정 온도 (℃) (Temperature) | 기타 사항 (Other details) |
|---|---|---|---|
| 금(gold) | 129 | 25 | - |
| 은(silver) | 233 | 25 | - |
| 구리(copper) | 385 | 25 | - |
| 자석(magnet) | 460–502 | - | - |
| 페라이트(ferrite) | 800 | - | - |
| 알루미늄(aluminum) | 897 | 25 | - |
| 공기 | 1,012 | 25 | - |
| 물 | 4,181.3 | 25 | - |
식 (6)을 식 (5)에 대입하면 최종적인 열 방정식을 다음과 같이 얻을 수 있다.
 (7)
(7)
열 전도도, 비열 용량, 질량 밀도가 시간과 공간에 대해 상수라면, 식 (7)은 다음처럼 단순화된다.
 (8)
(8)
여기서
[열 방정식의 쉬운 풀이]
열에 대한 물리학이 제대로 정립되지 않은 상태에서 식 (7), (8)과 같은 열 방정식을 제안한 부분이 대단하지만, 푸리에는 한걸음 더 나아가서 이런 편미분 방정식을 풀 수 있는 일반적인 해법을 제안했다. 요즘 말로 하면 변수 분리법(separation of variables)과 푸리에 급수(Fourier series)가 된다.

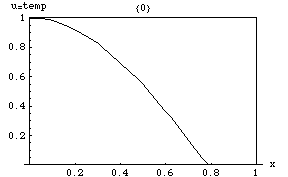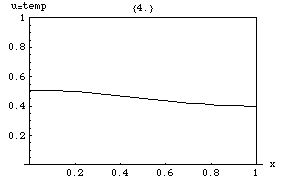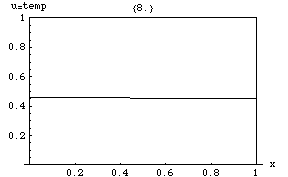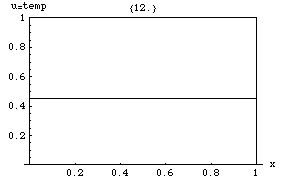
[그림 4] 1차원 온도 분포(출처: wikipedia.org)
푸리에 방법론을 이해하기 위해 [그림 4]에 제시한 문제를 풀어본다. 우리가 구해야 하는 온도 분포는
 (9)
(9)
변수
 (10)
(10)
식 (10)을 식 (9)에 대입해서 변수
 (11)
(11)
여기서
 (12)
(12) (13)
(13)
식 (12), (13)에서 얻은 기저 함수(basis function)를 합쳐 임의의 온도
 (14)
(14)
여기서
 (15)
(15)
식 (15)에서 임의 함수
 (16)
(16)
여기서
식 (10)에 사용한 변수 분리법이 성립하려면 식 (8)에서 얻은 편미분 방정식의 유일성 정리(uniqueness theorem)를 반드시 증명해야 한다. 만약 계산 방법에 따라 답이 제각각 얻어진다면 우리가 유도한 편미분 방정식 (8)은 물리적으로 의미가 없어진다.[∵ 조건이 같은데 온도가 두 개일 수는 없지 않나!] 유일성이 성립한다면 어떤 방법으로 답을 얻든지 동일한 결과를 도출하므로, 푸리에의 변수 분리법은 매우 강력한 편미분 방정식 해법이 된다. 유일성 증명을 위해 식 (9)에 있는 1차원 열 방정식의 서로 다른 해를
 (17)
(17)
여기서
 (18)
(18)
식 (18)에 의해
 (19)
(19)
두 해의 차이에 해당하는
 (20)
(20) (21)
(21)
따라서 3차원에서도
 (22)
(22)즉,

 (23)
(23)여기서
[참고문헌]
[1] J. Fourier, Théorie de la Propagation de la Chaleur dans les Solides (Theory of the Propagation of Heat in Solids), 1807.
[2] T. N. Narasimhan, "Fourier’s heat conduction equation: history, influence, and connections," Reviews of Geophysics, vol. 37, pp. 151–172, Feb. 1999.
[3] J. Fourier, Théorie Analytique de la Chaleur (Analytical Theory of Heat), 1822.
[5] 이정오, "무한급수의 총합 가능성과 후세인 보르에 관하여", 한국수학사학회지, 제30권, 제6호, pp. 353–365, 2017년 12월.
[6] Material Properties, "Polystyrene." (방문일 2023-05-26)
[다음 읽을거리]
1. 푸리에 급수의 시작










 (7)
(7)






 (1)
(1)

 (3)
(3)





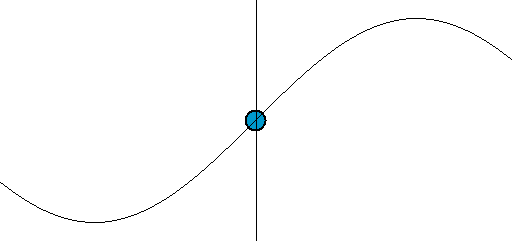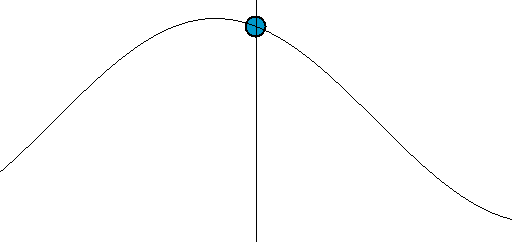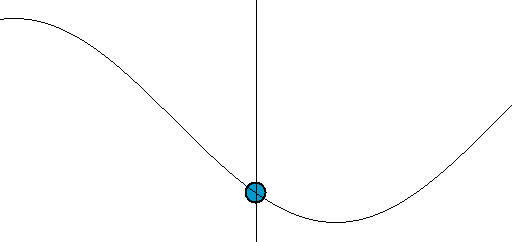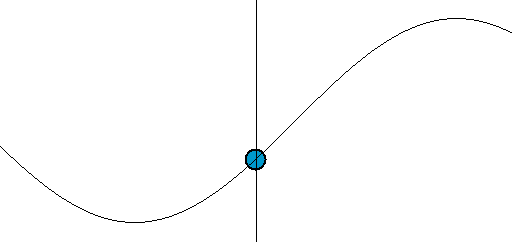

 (9)
(9)








 (16)
(16)
 (18)
(18)