[경고] 아래 글을 읽지 않고 "급속 하강 방법"을 보면 바보로 느껴질 수 있습니다.
임의의 함수를 엄밀하게 적분하기(integration)는 거의 불가능한 수학적 목표이다. 하지만 특별한 조건에서는 모든 함수를 아주 쉽게 적분할 수 있다. 먼저 특정 경로 $c$에 대한 복소 적분(complex integration)을 생각한다.
 (1)
(1)여기서 $x$는 매우 큰 양의 실수, $f(t)$는 해석적인(analytic) 복소 함수(complex function), $g(t)$는 $e^{x f(t)}$보다 천천히 변한다. 추가적으로 $x$가 커짐에 따라 $e^{x f(t)}$는 ($+$)와 ($-$)값 사이를 매우 빠르게 진동한다고 가정한다.[혹은 지수 항 $x f(t)$가 복소수(complex number)라서 복소 지수 함수(complex exponential function)의 특성을 가진다고 가정한다.]

[그림 1] 함수 $f(t)$ = $\cos (x t^2)$의 변화
예시적으로 [그림 1]에서 함수 $f(t)$ = $\cos (x t^2)$이 $t$ $\approx$ $0$ 근방에서 변화되는 특성을 관찰한다. 값 $t$ = $0$에서 멀어짐에 따라 함수는 매우 빠르게 변하지만, $t$ $\approx$ $0$ 근방에서는 함수값이 천천히 바뀐다. 큰 수 $x$를 계속 더 증가시키면, 적분값 $\int_c f(t) dt$는 $t$ $\approx$ $0$ 근방만 계산해도 된다. 오일러의 공식(Euler's formula)을 이용해 실 함수(real function)를 복소 영역으로 확장해도 마찬가지이다. 즉 복소 함수 $f(t)$ = $e^{ix t^2}$은 $\cos (x t^2) + i \sin (x t^2)$으로 바꿀 수 있어서 $t$ $\approx$ $0$ 근방에서는 $f(t)$ $\approx$ $\cos (x t^2)$만 생각해도 된다. 그래서 매우 큰 $x$에 대해 적분값 $\int_c f(t) dt$는 $\int_c \cos (x t^2) dt$와 거의 같다. 더 나아가서 [그림 1]에서 찾은 경험적 관찰이 수학적으로 타당한지 검증해본다. 이를 위해 해석 함수(analytic function) $f(t)$를 복소 영역에서 테일러 급수(Taylor series)로 전개한다.
 (2)
(2)여기서 $f'(t)$와 $f''(t)$는 각각 $f(t)$의 1계 및 2계 미분(the first and second differentiation)이다.


[그림 2] 안장점(saddle point)은 $x$ = $0$(출처: wikipedia.org)
[그림 1]과 같은 형태로 만들기 위해 $f'(t_s)$ = $0$이라 가정한다. 그러면 $f(t)$는 $t$ $\approx$ $t_s$ 근처에서 다음처럼 근사화된다.
 (3)
(3)이때 [그림 2]와 같은 $f(t)$의 모양에서 $t$ = $t_s$는 안장(saddle)과 같은 형태라서 안장점(saddle point)이라 한다. 안장점은 [그림 3]의 말 안장처럼 복소 함수의 어떤 단면에서는 최소값이고 다른 단면에서는 최대값인 점이다. 예를 들어, $z^2$ = $x^2 - y^2 + i 2xy$를 고려한다. 단면 $x$ = $0$에서 실수부는 최대값을 $y$ = $0$에서 가진다. 단면을 $y$ = $0$으로 선택하면, 실수부는 $x$ = $0$에서 최소값이 된다. 그러면 안장점 정의에 따라 원점인 $z$ = $0$이 안장점이다. 안장점을 찾는 쉬운 방법은 편미분이다. 이때 곡면의 접선 기울기가 0이 되면서 극값(extreme value)은 아닌 점이 안장점이다.[∵ 극값이면 단순히 최대값이나 최소값만을 가지기 때문에 급속 하강 경로가 생기지 않는다.] 1변수인 경우에 안장점이 생기는 특별한 예는 [그림 2]에 보인 $f(x)$ = $x^3$이다. 점 $x$ = $0$에서 $f'(x)$ = $0$이면서 극값은 생기지 않아서, 이 점이 바로 안장점이다.
안장점 부근에는 [그림 2]처럼 함수가 급격히 하강하는 경로인 급속 하강 경로(steepest descent path, SDP)가 존재한다. 원래 함수의 적분 경로를 잘 변형해서 급속 하강 경로를 따라 점근적으로 적분하는 방법이 바로 급속 하강 방법(method of steepest descent)이다. 급속 하강 방법은 리만Bernhard Riemann(1826–1866)이 1863년리만 37세, 조선 철종 시절에 제안한 방법을 바탕으로 디바이Peter Debye(1884–1966)가 1909년디바이 25세, 대한제국 시절에 처음으로 사용하였다.

[그림 3] 말 안장(출처: wikipedia.org)
안장점은 함수값이 증가하지도 감소하지도 않는 점일 수 있어서 정상점(stationary point)에 포함된다. [그림 4]에서는 증가하지도 감소하지도 않아서 미분값이 $0$인 빨간색 점이 정상점이다. 다만 정상점 중에서 극값이 없어야 안장점이 되므로, 정상점은 안장점이 되기 위한 필요 조건이다. [그림 4]처럼 적분 경로를 따라갈 때, 안장점은 여러 개일 수 있어서 $f(t)$의 안장점은 $N$개라고 가정한다. 예를 들어, $n$번째 안장점은 $t$ = $t_n$이다.

[그림 4] 정상점의 예시(출처: wikipedia.org)
식 (3)을 이용해서 $x$가 매우 커질 때, 식 (1)을 점근적으로 쓰면 다음과 같다.
 (4)
(4)여기서 $\delta$는 임의로 작은 양의 실수이다. 식 (4)에 나온 적분을 계산하려면, 적절한 변수 치환을 해야 한다. 복소 함수론 관점에서 변수 치환은 적분 경로의 변경이다. 급속 하강 방법에서는 원래 적분 경로를 식 (3)으로 표현된 급속 하강 경로로 바꾸어 계산한다. 그래서 다음과 같은 변수 치환 혹은 적분 경로 변경을 이용해 식 (4)의 적분을 다시 표현한다.
 (5)
(5)여기서 $|u_{\max}|$ = $\sqrt{x |f''(t_n)|} \delta$, 실수인 $u$는 항상 $-\infty$에서 $\infty$로 변하며, 마지막 적분은 가우스 함수(Gaussian function)로 유도한다. 식 (5)의 첫째식은 $t$에 대한 복소 적분 경로[$\int_c \,dt$]가 $u$에 대한 실수 적분 경로[$\int_{-\infty}^\infty \,du$]로 바뀜을 의미한다. 또한 식 (5)에 있는 부호 $\pm$는 ($+$)와 ($-$) 둘 다 가능하다는 뜻이 아니다. 변수 $t$에서 $u$로 적분 경로를 변형할 때는 해석적이어야 하므로, ($+$)와 ($-$) 둘 중 하나만 잘 선택해서 $t$와 $u$의 적분 경로가 서로 일관되도록 계산해야 한다. 일례로 $f(z)$ = $z$ = $x +iy$를 기준으로 $z^*$ = $x -iy$는 코쉬–리만 방정식(Cauchy–Riemann equation)을 만족하지 못해서 해석적이 아니다. 또한 기하학적으로 $z$가 복소 평면에서 반시계 방향으로 회전한다면, $z^*$는 시계 방향으로 돈다. 그래서 적분 경로가 돌아가는 방향에 따라 해석적이 될 수도 있고 아닐 수도 있다. 이러한 해석적인 선택을 의미하는 표식이 식 (5)의 부호 $\pm$이다. 이를 종합해서 식 (5)를 식 (4)에 대입해서 급속 하강 방법을 이용한 적분 결과를 다음처럼 공식화할 수 있다.
 (6)
(6)여기서 변수 치환은 $t$ = $\pm i u / \sqrt{x f''(t_n)}$, 부호 $\pm$ 중에서 변수 치환한 적분 경로가 서로 일관되도록 ($+$) 혹은 ($-$)값을 선택한다.
 (7)
(7)여기서 $k^2$ = $\xi^2 + \eta^2$, $\rho^2$ = $x^2 + y^2$이다. 식 (7)의 좌변을 식 (1)처럼 만들기 위해 다음처럼 변수 치환한다.
 (8)
(8)여기서 $y \ge 0$, $\xi$ = $k \sin w$, $\eta$ = $\sqrt{k^2 - \xi^2}$ = $k \cos w$, $x$ = $\rho \cos \phi$, $y$ = $\rho \sin \phi$, $\eta$에 의해 [그림 5]와 같은 가지 자름(branch cut)이 생긴다.

[그림 5] 급속 하강 방법을 위한 급속 하강 경로
[그림 5]에 표현한 변수 $\xi$를 변형한 급속 하강 경로(SDP)는 다음처럼 정의할 수 있다.
 (9)
(9)제곱근 함수에 의해 생기는 가지 자름을 가진 $\eta$의 관계식은 다음과 같다.
 (10)
(10)식 (10)과 [그림 5]의 SDP를 보면, $\eta$의 실수부는 모든 경로에서 $0$보다 크고 허수부는 $0$보다 크거나 같다. 즉 $\eta$ = $k \cos w$는 전자파의 복사 조건(radiation condition)을 만족하도록 택한다는 뜻이다. 식 (8)에 있는 지수를 복소 영역에서 테일러 급수(Taylor series)로 전개해서 안장점 $w_s$를 구한다.
 (11)
(11)식 (11)을 식 (8)과 (6)에 대입해서 정리한다.
 (12)
(12)여기서 $f''(w_s)$ = $-i$, 변수 치환은 $w$ = $w_s \pm i u/\sqrt{-i}$이다. 변수 $u$는 항상 $-\infty$에서 $\infty$인 경로를 택하므로, [그림 5]에 의해 $u > 0$인 경우는 안장점 근처에서 $w$의 실수부는 양, 허수부는 음이다. 그래서 변수 치환의 부호를 ($-$)로 택해서 $-e^{i3\pi/4}$ = $e^{-i \pi/4}$를 얻는다. 비슷한 방법으로 식 (7)과 약간 다른 복사 적분의 점근식도 쉽게 유도할 수 있다.
 (13)
(13) (14)
(14)식 (11)과 비슷하게 식 (14)를 위한 안장점을 구한다.
 (15)
(15)변수 치환 $w$ = $w_s \pm i u/\sqrt{-i}$의 부호를 ($-$)로 선택한 후 식 (15)를 식 (6)에 대입하면, 식 (13)을 증명할 수 있다.
전자파 산란 적분이 이중 적분 형태이더라도 식 (7) 혹은 (13)을 차례로 적용해서 점근식을 구한다. 예를 들어, 다음과 같은 3차원 적분의 점근식을 구해보자.
 (16)
(16) (17)
(17)여기서 $\kappa^2$ = $k^2 - \eta^2$, $s^2$ = $r^2 - y^2$, $\xi$ = $\kappa \sin w$, $\zeta$ = $\kappa \cos w$, $x$ = $s \cos \alpha$, $y$ = $s \sin \alpha$이다. 다시 식 (17)에 식 (13)을 대입해서 적분을 모두 없앤다.
 (18)
(18)여기서 $\eta$ = $k \sin w$, $\kappa$ = $k \cos w$, $y$ = $r \sin \beta$, $s$ = $r \cos \beta$이다. 식 (18)에 나오는 각도 $\alpha, \beta$는 생소하기 때문에, 다음 관계식을 이용해 통상적인 구 좌표계(spherical coordinate system)로 바꾸면 식 (16)이 증명된다.
 (19)
(19)이를 모두 종합하면, 식 (13)은 2차원 공간, 식 (16)은 3차원 공간에 대한 푸리에 변환을 급속 하강 방법에 따라 점근적으로 구한 획기적인 결과이다. 식 (16)에 나온 적분 변수는 좌표 성분의 선택에 따라 다음처럼 표현할 수도 있다.
 (20a)
(20a) (20b)
(20b)따라서 $r$이 커질 때에 이중 적분에 최종적으로 기여하는 성분은 정확히 $\bar k$ = $k \hat r$이다.
2차원과 3차원에 대한 급속 하강법을 하나로 통일하는 방법은 그린 함수(Green's function)를 활용한다.
 (21a)
(21a) (21b)
(21b)여기서 $H_0^{(1)}(\cdot)$은 제0차 제1종 한켈 함수(the zeroth-order Hankel function of the first kind)이다. 식 (21)에 등장하는 $-2$인 계수와 편미분은 1차원 자유 공간 그린 함수(1D free-space Green's function)로 설명한다. 그린 함수 정의에서 원천을 $-\delta(x-x')$로 사용해서 ($-$) 부호가 나온다. 1차원에서 파동은 양방향인 좌우로 복사된다. 하지만 우리는 식 (21)에서 한 방향으로만 가는 균일 평면파(uniform plane wave)를 선택하므로, 원래 값에서 2배가 되어야 한다. 또한 식 (21)의 피적분 함수는 단순한 복소 지수 함수라서 그린 함수를 진행 방향으로 편미분한다.

 (2)
(2) (3)
(3) (4)
(4)


 (8)
(8) (9)
(9)


 (12)
(12)

 (15)
(15) (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3)

 (1.7)
(1.7)
 (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11)
 (1.13)
(1.13)
 (1.15)
(1.15) (2.1)
(2.1)

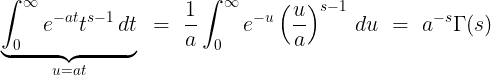

 (2.6)
(2.6) (2.7)
(2.7)
 (2.9)
(2.9)
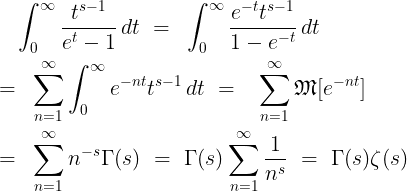 (2.11)
(2.11) (2.12)
(2.12)



 (3.5)
(3.5)
 (3.7)
(3.7) (3.8)
(3.8)