1. 전송선 이론
[확인] 본 페이지는 exp(jωt) 시간 약속을 사용하고 있습니다.

[그림 1] 원천과 부하를 연결하는 전송선(출처: wikipedia.org)
식 (1)의 전송선 방정식(transmission line equation)으로부터 직접적으로 얻어지는 결론은 전송선 이론(transmission line theory)의 전압과 전류는 더이상 회로 이론(circuit theory)의 전압과 전류가 아님이다.
 (1)
(1)
여기서 $R, L, G, C$는 단위길이당 해당 회로량을 의미한다. 예를 들어 $R$의 단위는 Ω/m이다. 이를 확인하기 위해 식 (1)을 $z$에 대해 미분한다.
 (2)
(2)
식 (2)는 전형적인 상수 계수(係數常數, constant coefficient) 선형 상미분 방정식(常微分方程式, linear ordinary differential equation: 하나의 독립 변수만 가진 선형적인 미분 방정식)이므로 식 (2)의 답을 아래로 가정하고 식 (2)에 대입한다.
 (3)
(3)
그러면 미지수인 $\gamma$를 결정할 수 있다.
 (4)
(4)
식 (4)를 식 (3)에 대입해보면 식 (2)를 만족하는 해는 두 개임을 알 수 있다. 따라서, 전송선에 발생하는 전체 전압과 전류는 아래로 표현할 수 있다.
 (5)
(5)
여기서 $V(z)$, $I(z)$는 회로 이론에서 배운 우리가 잘 아는 전압과 전류이며, $V_0^+$, $V_0^-$, $I_0^+$, $I_0^-$는 전송선 이론에 새로 도입된 파동의 진폭을 나타내는 계수로서 전압과 전류에 대한 경계 조건(境界條件, boundary condition)을 이용하여 정하게 된다. 식 (5)의 $V_0^+$, $V_0^-$, $I_0^+$, $I_0^-$에 있는 ($+$)와 ($-$)는 파동의 진행 방향이다. 즉, ($+$)는 $+z$축, ($-$)는 $-z$축으로 진행하는 파동을 뜻한다. 따라서, $V_0^+$와 $I_0^+$는 $+z$축, $V_0^-$와 $I_0^-$는 $-z$축으로 진행하는 전압파와 전류파의 크기와 $z$ = $0$에서의 기준 위상을 표현한다. 또한, 식 (5)는 페이저(phasor)를 이용하여 시간 변동을 없앤 결과이기 때문에 실제로는 공간과 시간에 대해 전송선의 전압과 전류가 변하게 된다. 공간과 시간에 대해 식 (6)과 같이 변하면 파동(波動, wave)이라 하므로 전송선의 전압과 전류는 반드시 전압파(voltage wave)와 전류파(current wave)로 생각해야 한다.
 (6)
(6)
전압파와 전류파는 회로 이론과 전송선 이론을 구별하는 매우 중요한 개념이다. 식 (5)와 (6)에서 $I_0^-$의 앞 부호는 ($-$)로 선택한다.[부호를 ($+$)로 택해도 전혀 문제없다.] 반사 전류파는 입사 전류파와 흐르는 방향이 다르다고 가정하면 편하므로 이렇게 정한다.
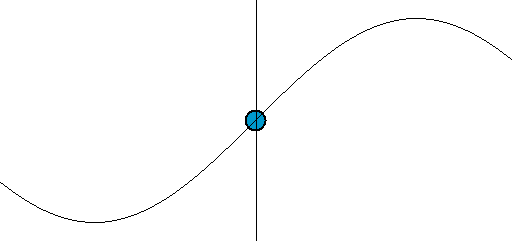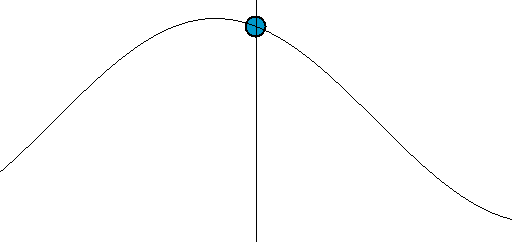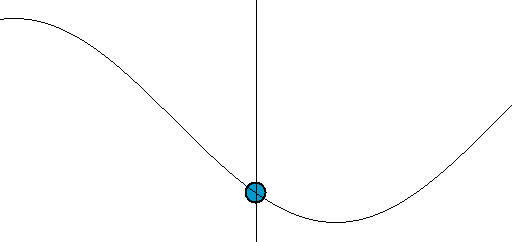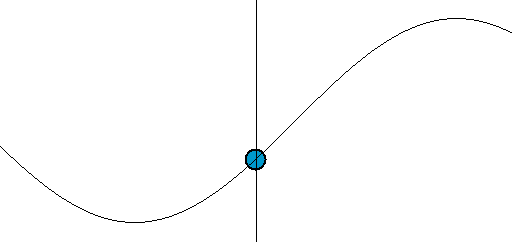
[그림 2] 전압파와 전류파의 움직임(출처: wikipedia.org)

[그림 3] 파면의 개념(출처: wikipedia.org)
[그림 2]처럼 전압파와 전류파는 전송선의 위치와 주어진 시간에 따라 계속 변하기 때문에 회로 이론처럼 어느 지점의 전압과 전류를 측정하기는 의미가 없다.[∵ 해당 위치에서 계속 변하기 때문이다.] 그래서, 전압파와 전류파가 이송하는 평균 전력(平均電力, average power)이 전송선 이론의 중요 지표이다.[평균 전력을 알려면 반사 계수(reflection coefficient)를 계산해야 한다.] 식 (6)을 잘 관찰하면 회로 이론과 전송선 이론의 차이점을 발견할 수 있다. 식 (6)의 좌변은 AC 회로 이론에서 측정하는 양이다.[∵ 전송선 방정식은 회로 이론을 기반으로 유도하기 때문에 $V(z), I(z)$는 회로 이론 양이다.] 식 (6)의 우변은 서로 반대 방향으로 진행하는 전압파와 전류파의 합성이다. 즉, 회로 이론의 전압과 전류를 파동의 성질을 가진 전압파와 전류파의 합성으로 설명할 수 있다. 예를 들면 식 (5)의 $V(z)$, $I(z)$가 회로 이론에서 정의한 전압과 전류이다. 이 전압과 전류는 전송선 이론의 입사[$V_0^+$항] 및 반사[$V_0^-$항] 전압파, 입사[$I_0^+$항] 및 반사[$I_0^-$항] 전류파로 분해해서 더 구체적으로 생각할 수 있다.
식 (6)의 우변이 파동을 의미한다는 뜻을 이해하기 위해 복소수(complex number)인 전파 상수(傳播常數, propagation constant) $\gamma$를 실수부와 허수부로 구분한다.
 (7)
(7)
여기서 $\alpha$는 감쇠 상수(attenuation constant), $\beta$는 위상 상수(phase constant)이다. 감쇠 상수는 파동이 진행함에 따라 진폭이 얼마나 감소하는지를 나타내며 위상 상수는 파동의 진행에 따른 위상의 변동을 나타내는 상수이다. 위상 상수를 이용해 새로운 용어인 관내 파장(管內波長, guided wavelength) $\lambda_g$을 정의한다.
 (8)
(8)
관내 파장은 전송선 내부에 존재하는 등가적인 파장(equivalent wavelength)을 뜻한다. 관내 파장은 전송선 매질과 기학 구조에 의해 결정된다.[더 정확하게 하려면 전송선의 모드(mode)까지 고려해야 한다.] 그래서 파동 방정식에 등장하는 파수(波數, wavenumber)를 위상 상수로, 파장을 관내 파장으로 비유해서 생각할 수 있다. 식 (7)을 식 (6)에 대입해서 위상만 고려하면 파동의 진행 방향도 얻을 수 있다.
 (9)
(9) (10)
(10)
파동의 움직임을 이해하려면 [그림 3]에 있는 파면(波面, wavefront)을 봐야 한다. [그림 3]을 보면 직관적으로 파동이 움직임을 느낄 수 있다. 파동이 왼쪽에서 오른쪽으로 움직이는 변화를 어떻게 인지할 수 있을까? 왜냐하면 우리가 눈으로 파면[예를 들면 꼭대기나 골짜기 등]을 추적해서 움직임을 이해하기 때문이다. 마찬가지로 식 (9)와 (10)에서 기준 파면을 $\phi_0$ = $0^\circ$인 지점으로 간주하면 이해가 된다. 시간이 $\Delta t$만큼 흐르면 식 (9)에 $\Delta z$가 $+z$ 방향으로 움직이고 식 (10)에서는 $\Delta z$가 $-z$방향으로[즉, 식 (9)와는 반대 방향으로] 움직인다. 이렇게 되는 이유는 위상 상수의 부호가 다르기 때문이다. 즉, 위상 상수가 ($+$)이면 파동은 $-z$방향으로 움직이며 위상 상수가 ($-$)이면 파동은 $+z$방향으로 움직인다. 따라서, 식 (6)의 $V_0^+, I_0^+$는 $+z$방향으로 움직이는 전압파와 전류파의 진폭이며 $V_0^-, I_0^-$는 $-z$방향으로 움직이는 전압파와 전류파의 진폭이다. 또한, 식 (9)처럼 주파수와 관내 파장의 곱이 전압파와 전류파가 움직이는 속도가 된다. 이 속도는 매질 특성인 $R, L, G, C$와 주파수에만 관계되는 상수이다. 식 (5)의 둘째식을 보면 $I_0^-$의 부호를 ($-$)로 설정한다. 이런 변화는 좀 이상하다. 이렇게 하는 이유는 전류의 방향을 바꾸기 위해서이다.[∵ 전류의 위상을 180˚ 바꾸면 전류 방향이 바뀐다.] 식 (5)와 같이 정의하면 파동의 진행 방향과 전류의 방향을 동일하게 만들 수 있어 계산할 때 매우 편해진다.[예를 들어 $I_0^-$의 부호를 ($+$)로 하면 파동은 $-z$쪽으로 움직이지만, 전류의 기준 방향은 $+z$방향이 되어 매우 불편해진다. 그래서, $I_0^-$의 부호를 ($-$)로 바꾸면 전류가 ($+$)인 방향은 $-z$쪽이 되어 계산이 편해진다.]
이상의 논의를 바탕으로 우리는 회로를 해석할 때 경우에 따라 회로 이론이나 전송선 이론을 사용할 수 있다. 언제 회로 이론을 쓰고 언제 전송선 이론을 써야 하나? 물론 전송선 이론이 정확하기 때문에 모든 회로 해석에 쓰일 수 있지만 너무 복잡하다. 회로 이론을 쓸 수 있는 곳에는 회로 이론을 쓰면 된다. 경험적으로 전송선 이론을 써야 하는 기준은 시스템의 크기 $D$가 관내 파장의 1/100보다 커지는 $D > \lambda_g / 100$ 경우이다. 예를 들어, 전송선의 길이를 1/100 파장으로 놓고, 회로 이론과 전송선 이론 간에 발생하는 위상 차이를 계산한다. 회로 이론에서는 단락된 도선을 따라 움직여도 신호의 위상은 변화가 없기 때문에, 위상차는 0˚라 생각한다. 반면 전송선에서는 전압파와 전류파의 이동으로 인해 필연적으로 위상 변화가 다음처럼 생긴다.
 (11)
(11)
겨우 3.6˚라고 할 수도 있지만 판단 기준이 필요하기 때문에, 회로 이론을 쓸 수 있는 시스템의 크기 한계는 관내 파장의 1/100이라 생각한다. 시스템이 관내 파장보다 매우 작으면 아래 근사가 성립한다.
 (12)
(12)
식 (12)의 우변 근사식은 많이 보던 모양이다. 이 식은 AC 회로 이론에서 사용한 페이저(phasor)이다. 사용하는 주파수가 매우 낮거나[혹은 사용하는 파장이 매우 길거나] 시스템의 크기가 매우 작으면 페이저[혹은 AC 회로 이론]만 쓰더라도 전압과 전류를 잘 예측할 수 있다. 거꾸로 주파수가 매우 높아지거나 시스템의 크기가 커진다면 회로 해석에 반드시 전송선 이론을 써야 한다.
식 (4)에서 $R$ = $G$ = $0$이 되면, 손실 없는 전송선(lossless transmission line)의 전파 상수가 된다.
 (13)
(13)
손실을 일으키는 $R, G$가 없기 때문에 감쇠 상수가 0이 되어 손실이 없음은 당연하다. 이 경우 파동의 속도 $v$는 주파수에 관계없이 $L, C$에만 관계되어 항상 일정하게 된다.
 (14)
(14) (15)
(15) (16)
(16)
여기서 $L_{\rm ckt}, C_{\rm ckt}$는 회로 이론의 인덕턴스(inductance)와 전기 용량(capacitance)이다. 다음으로 전송선 내부에 존재하는 전자기파(electromagnetic wave)는 TEM(횡전자기, Transverse ElectroMagnetic: 진행 방향으로 전기장과 자기장 성분이 없음)파라 가정한다. TEM파는 전기장과 자기장이 서로 수직이며 전기장과 자기장의 비율[파동 임피던스: wave impedance]이 항상 일정하다. 그래서, 식 (15)와 (16)을 표현하는 좌표계를 간단하게 $(t_e, t_h, z)$로 정한다. 여기서 $t_e$는 전기장 방향 좌표이며 $t_h$는 자기장 방향 좌표이다.
 (17)
(17)
그러므로, 전송선에 존재하는 파동의 속도는 항상 아래 식을 만족한다.
 (18)
(18)
식 (18)은 전송선 내부에 전압파와 전류파가 존재하지만 손실이 없는 경우 그 파동의 속도는 전자기파의 속도(velocity of electromagnetic wave)와 동일함을 의미한다. 실제 전송선은 항상 손실을 가지기 때문에 $R$ = $G$ = $0$이라는 가정은 현실적이지 않다. 그래서 저손실 전송선(low loss transmission line) 개념을 도입한다. 손실이 낮으면 $R, L, G, C$ 관점에서 $R \ll \omega L$, $G \ll \omega C$라 가정한다. 그러면 식 (4)는 아래처럼 간략화된다.
 (19)
(19)
식 (19) 유도를 위해 거듭제곱 함수(square root function)의 테일러 급수(Taylor series)를 이용한다. 재미있게도 식 (19)의 위상 상수는 손실 없는 전송선의 위상 상수인 식 (13)과 동일하다. 또한 실제 전송선로는 대부분 저손실 조건을 만족하기 때문에,[∵ 손실이 많으면 제품으로 판매할 수 없다.] 손실이 조금 있더라도 위상 상수 측면에서는 손실 없는 전송선으로 식 (19)처럼 근사가 가능하다. 그래서 실무에서는 식 (13)을 이용해 위상 상수를 근사적으로 정의한다. 식 (19)에 나타난 감쇠 상수 다음과 같이 특성 임피던스(characteristic impedance) $Z_0$를 이용해 더 간략히 표현할 수 있다.
 (20)
(20)여기서 $Z_0$ = $\sqrt{L/C}$ = $V_0^+/I_0^+$ = $V_0^-/I_0^-$이다. 식 (20)에 의해 $R$이 $G$보다 우세한 전송선로에서는 $Z_0$를 크게 설계해서 신호의 감쇠를 줄인다. 이는 전압파와 전류파의 특성에 기인하는 자연스러운 현상이다. 전송선로에 전류가 직렬로 흐를 때 생기는 손실 전력은 $R I^2$에 비례한다. 즉, 전류가 직렬로 흘러서 생기는 손실은 전류 자체를 줄여야 작아진다. 따라서 $Z_0$를 키우면 전압파 대비해서 전류파가 작아지기 때문에 전송선로에 생기는 전류가 줄어들어서 손실 전력이 작아진다. 이러한 전류파와 손실 전력의 관계를 식 (20)이 잘 설명하고 있다. 저항 밀도 $R$이 큰 경우와 비슷하게 컨덕턴스 밀도 $G$가 우세한 전송선로의 손실을 감소시키려면 $Z_0$를 줄여야 한다. 왜냐하면 전송선로에 병렬로 전압이 걸려서 생기는 손실은 $G V^2$에 비례하므로 $V$를 줄여야 감쇠가 줄기 때문이다. 그래서 $Z_0$를 줄이면 전류파 대비 전압파가 감소해서 $G$에 의한 손실도 적어진다.
[다음 읽을거리]
1. 특성 임피던스의 이해
2. 전압파의 반사 계수
3. 반사 전력과 투과 전력






 (1)
(1)



 (1)
(1)
 (3)
(3) (4)
(4) (5)
(5) (1.1a)
(1.1a) (1.1b)
(1.1b)

 (1)
(1) (2)
(2)
 (3)
(3)
 (4)
(4) (5)
(5) (6)
(6) (7)
(7)
 (8)
(8)