[경고] 아래 글을 읽지 않고 "라플라스 변환"을 보면 바보로 느껴질 수 있습니다.
[라플라스 변환 소개]
푸리에 변환(Fourier transform)은 단순 정적분(definite integral)에 해당하는 유한 구간 적분에 강하다. 만약 $t$ 혹은 $\omega$에 대한 적분 구간이 무한(infinite)[$-\infty < t < \infty$]이나 반무한(semi-infinite)[$t \le c$ 혹은 $t \ge c$]으로 가면, 푸리에 변환 혹은 역변환은 적분이 잘 구해지지 않는다.
 (1)
(1)무한한 적분 구간에서 식 (1)의 결과를 안정되게 구할 때는 감쇠를 이용한 극한(limit)이나 복소 함수론(complex analysis)에 기반한 경로 적분을 적극적으로 써야 한다. 하지만 이러한 방법론은 너무 수학적이라서 쉽게 쓰려고 도입한 적분 변환(integral transform)의 취지에 적합하지 않다. 푸리에 변환이 유용해서 버리기는 아깝지만 무한 영역의 적분에서 문제가 분명히 생긴다. 이러한 애매함을 감쇠라는 현실적인 양으로 해결한 엄청난 도구가 바로 라플라스 변환(Laplace transform)이다.
 (2)
(2)여기서 $s$ = $\sigma + i \omega$, $\sigma$는 감쇠(減衰, attenuation)이다. 라플라스 변환은 천제 현상을 기술하는 미분 방정식(differential equation)을 풀기 위한 라플라스Pierre-Simon Laplace(1749–1827) 노력의 결정체이다[2]. 후에 헤비사이드Oliver Heaviside(1850–1925)가 라플라스 변환을 재발견하고 현재와 같은 쓰임새를 만들어냈다.
식 (2)에 도입한 $\sigma$가 너무 작위적이라 생각할지도 모른다. 그러나 현존하는 모든 시스템은 크던 작던 감쇠가 있기 때문에, 감쇠없이 항상 진동한다는 푸리에 변환이 오히려 현실에 잘 맞지 않고, 시간에 따라 감쇠한다는 라플라스 변환이 더 현실적이다.

[그림 1] 시스템 과도 응답의 예(출처: wikipedia.org)
라플라스 변환은 적분이 $0$부터 시작하므로 [그림 1]과 같은 과도 응답(transient response)의 분석에 적합하다. 푸리에 변환은 적분의 시작과 끝이 무한대라서 사실 응답의 시작과 끝이 없다. 그래서 푸리에 변환은 정현파처럼 끊임없이 반복적인 정상 상태 응답(steady-state response)의 분석에 좋다. 라플라스 변환과 푸리에 변환의 관계는 다음과 같다.
 (3)
(3)여기서 $u(t)$는 단위 계단 함수(unit step function)이다. 푸리에 변환이 실패한 무한 적분 유도가 라플라스 변환에서는 연습 문제 수준인 이유를 식 (3)에서 명확히 볼 수 있다. 라플라스 변환에는 적분을 강제로 수렴시키는 감쇠 $\sigma$와 함께 단방향 적분을 만드는 단위 계단 함수 $u(t)$가 필수 요소이다. 그래서 단위 계단 함수의 또 다른 이름인 헤비사이드 계단 함수(Heaviside step function)에 라플라스 변환의 제안자인 헤비사이드Oliver Heaviside(1850–1925) 이름이 들어간다.
라플라스 변환의 위력을 느끼기 위해 $u(t)$의 라플라스 변환을 구해보자.
 (4)
(4)반면에 $u(t)$에 대한 푸리에 변환을 구하려면, 로렌츠–코쉬 함수(Lorentz–Cauchy function)의 극한을 쓰거나 복소 함수론에 나오는 경로 적분(contour integral)을 사용해야 한다.
 (5)
(5)복소수 $s$ = $i \omega$로 두면 두 결과는 매우 비슷하다. 하지만 무한 적분을 계산할 때 사용한 수학 수준은 하늘과 땅만큼 차이난다.
식 (2)에 소개한 라플라스 변환은 푸리에 변환만큼 흔하게 볼 수 있는 적분 변환이다. 하지만 그 역인 라플라스 역변환(inverse Laplace transform)은 어떻게 표현할까? 아마 라플라스 역변환은 거의 본 적이 없을 것이다. 그러나 비슷하지만 다른 푸리에 역변환은 푸리에 변환만큼 자주 사용된다. 이런 차이는 어디서 오는 것일까? 라플라스 역변환과 관련된 멱급수(power series)의 수렴 조건과 원래 함수로의 일대일 대응 문제는 헤비사이드가 제안한 라플라스 변환이 수학자들에게 공격받은 주요 약점이었다. 이런 상황에서도 공학자 출신인 헤비사이드는 자신만의 변환 개념을 그대로 밀어붙여 미분 방정식의 놀라운 해법인 연산 미적분학(operational calculus)을 공학적으로 완성시켜 버렸다. 연산 미적분학과 복소 함수론(complex analysis)이 결합하면 자연스럽게 라플라스 변환이 만들어진다. 즉 복소 함수론으로 연산 미적분학을 완벽하게 개선한 결과물이 우리가 쓰는 라플라스 변환이다. 연산 미적분학의 수학적 엄밀성과 라플라스 역변환의 존재성을 헤비사이드 자신도 증명하지 못했지만 괜찮았다. 수학적 기반이 부족해도 헤비사이드의 연산 미적분학은 실무에서 완벽하게 잘 동작했다. 그래서 자신이 만든 연산 미적분학이 미분 방정식을 쉽게 푸는 새로운 세상을 열었다고 믿었다. 실제로도 공학자의 공부 분량을 현저하게 줄인 주요 개념이 연산 미적분학과 라플라스 변환이다. 헤비사이드가 그토록 바라던 연산 미적분학의 수렴성과 라플라스 역변환은 브롬위치Thomas John I'Anson Bromwich(1875–1929)가 복소 함수론을 도입하여 완전하게 해결했다. 이런 이유로 라플라스 역변환을 브롬위치 적분(Bromwich integral)으로도 부른다. 결국 복소 함수론에 의해 완전체가 된 연산 미적분학과 라플라스 변환은 수학자들의 뜨거운 찬사를 받으며 19세기 수학의 전설이 되었다.
[라플라스 역변환 혹은 브롬위치 적분]
 (6)
(6)여기서 $\sigma$는 복소 적분이 수렴하는 위치로 정한다.
[증명]
식 (6)의 우변에 식 (2)를 넣어서 적분을 정리한다.
 (7)
(7)
[그림 2] 브롬위치 적분을 위한 닫힌 경로
만약 식 (7)에서 $t \ne t'$이라면, 식 (7)의 복소 적분은 [그림 2]와 같은 닫힌 경로의 내부에 극점(pole)이 없다. 그래서 다음 적분은 코쉬의 적분 정리(Cauchy's integral theorem)에 의해 항상 $0$이다.
 (8)
(8)여기서 반원 경로의 반지름 $R$을 무한대로 보낸다. 시간이 $t > t'$와 $t < t'$일 때는 경로를 각각 $c_2$와 $c_3$로 택해서 닫힌 경로의 내부 영역이 잘 수렴하도록 한다. 이러한 조건에서 $R$을 계속 키우면, 푸리에 변환과 디랙 델타 함수의 증명과 동일하게 $c_2$와 $c_3$ 경로 상의 복소 적분은 각각 $0$으로 수렴한다. 따라서 $t \ne t'$이라면, 식 (8)에 의해 경로 $c_1$에 대한 적분도 당연히 $0$이 된다. 이 결과를 사용해 식 (7)에 있는 $t'$의 적분 영역을 $t - \Delta \le t \le t + \Delta$로 제한해도 된다. 시간 $t'$의 적분 영역을 매우 축소한 경우, 실수 $t'$와 복소수 $s$에 대한 적분을 다시 해본다.
 (9)
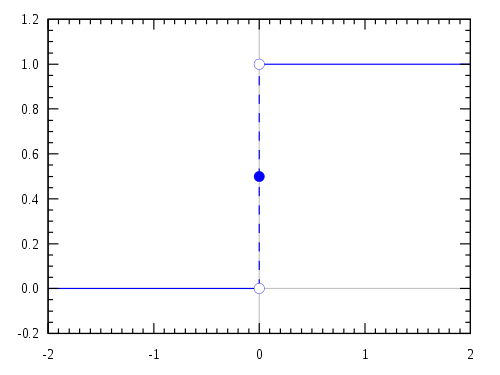
(9)닫힌 경로 $c_1 + c_2$ 내부에는 극점이 $z = 0$에 있어서 유수 정리(residue theorem)를 사용할 수 있다. 반대로 $c_1 + c_3$ 내부는 해석적이라서 극점이 없다. 그래서 이 경로를 사용한 복소 적분은 항상 $0$이다. 식 (8)과 (9)를 종합해서 다음과 같은 디랙 델타 함수(Dirac delta function)의 관계식을 얻는다.
 (10)
(10)식 (10)을 식 (7)에 대입하면, 쉽게 식 (2)의 결과를 증명할 수 있다.
______________________________
브롬위치 적분의 증명을 고찰하면, 브롬위치 이전 수학자들이 라플라스 역변환을 얻지 못했던 이유를 분명히 볼 수 있다. 푸리에 변환과 역변환의 적분은 실수 영역에서 둘 다 정의되어서 굉장히 상식적이다. 하지만 라플라스 변환은 실수 영역에서 1차원적 정적분(definite integral)을 하고 라플라스 역변환은 복소 평면에서 2차원적 선 적분(line integral)을 한다. 변환과 역변환이 서로 다른 영역과 적분 방식을 가져도 되는가? 라플라스 변환과 역변환이 가진 이러한 비대칭적 특성은 우리 상식에 반하지만, 식 (6)처럼 라플라스 역변환도 잘 정의된다. 그래서 헤비사이드가 처음에 가졌던 확신이 타당함을 브롬위치가 복소 함수론으로 확실하게 증명했다.
브롬위치 적분이 라플라스 역변환임을 더 극적으로 보기 위해, 평행 이동된 단위 계단 함수 $u(t-t_0)$의 라플라스 변환을 생각한다.
 (11)
(11)여기서 수렴을 위한 조건은 $\Re[s] > 0$이다. 식 (11)의 결과를 식 (6)에 대입해서 복소 적분을 계산한다. 만약 $t > t_0$이라면, [그림 2]에서 닫힌 경로를 $c_1+c_2$로 택해서 유수(residue)를 구한다.
 (12)
(12)반대로 $t < t_0$인 경우, 피적분 함수를 수렴시키기 위해 닫힌 경로는 $c_1+c_3$가 되어야 한다. 그러면 닫힌 경로 내부에 극점이 없어서 복소 적분은 $0$이 된다. 이 두 결과를 종합하면, $e^{-s t_0}/s$에 대한 식 (2)의 적분은 $u(t-t_0)$이다. 따라서 브롬위치 적분은 정확히 라플라스 역변환이다. 이상의 결과를 명확하게 명제로 표현하면 다음과 같다.
[라플라스 변환의 일대일 대응(one-to-one mapping)]
두 함수의 라플라스 변환이 같으면 두 함수는 유한한 점에서만 다르고 나머지 영역에서는 같다.
 (13)
(13)[증명]
라플라스 변환의 역변환이 존재하기 때문에 일대일 대응은 당연히 성립한다. 다만 라플라스 변환은 리만 적분(Riemann integral)으로 정의하므로, 유한한 점의 적분은 기여가 없다. 그래서 두 함수는 유한한 점에서 다를 수 있다.
______________________________
두 함수가 무한한 점에서 다를 경우는 디랙 델타 함수(Dirac delta function)가 있다는 뜻이다. 그래서 두 함수의 라플라스 변환은 같을 수 없다. 다시 말해 무한한 점에서 다르면 라플라스 변환의 일대일 대응이 잘 성립한다. 다만 이런 조건이 성립하려면 라플라스 변환이 잘 존재해야 한다. 식 (11)의 예에서 보듯이, 라플라스 변환을 구성하는 $s$에 따라 적분이 존재할 수도 혹은 없을 수도 있다. 식 (6)에 정의한 브롬위치 적분을 잘 조합하면 라플라스 변환에 대한 정확한 수렴 조건(convergence condition)을 얻을 수 있다.
[라플라스 변환의 수렴 조건]
라플라스 변환 $F(s)$의 극점보다 우반면(right half-plane)에 있는 $s$를 택해야 라플라스 변환이 수렴한다.
 (14)
(14)여기서 $\Re[s] > \sigma$이다.
[증명]
식 (6)을 식 (2)에 대입해서 정리한다.
 (15)
(15)여기서 지수 함수를 수렴시키기 위해 $\Re[s] > \sigma$인 조건을 택한다. 식 (15)의 마지막식은 아래에 있는 코쉬의 적분 공식(Cauchy's integral formula)과 매우 비슷하다.
 (16)
(16)식 (16)이 성립하기 위해서는 닫힌 경로 내부에서 $f(z)$가 해석적이어야 한다. 그래서 식 (15)에 있는 경로를 [그림 2]에 있는 $c_1 + c_3$으로 잡는다. 또한 $c_1 + c_3$ 내부에 $F(u)$의 극점이 있으면 안되므로, $F(u)$의 극점은 $s$의 좌반면(left half-plane)에 있도록 라플라스 변환의 $s$를 정한다. 그러면 코쉬의 적분 공식에 의해 식 (15)는 $F(s)$가 된다.
______________________________
푸리에 변환과 역변환은 동일한 실수 영역에서 적분이 이루어져서 증명 과정이 비슷하다. 하지만 라플라스 변환은 역변환과 적분 영역이 아주 달라서 상호간의 증명 과정도 서로 차이가 많이 난다. 라플라스 역변환에 변환을 대입한 식 (7)은 디랙 델타 함수(Dirac delta function)를 이용해 증명한다. 반면에 라플라스 변환에 역변환을 넣은 식 (15)의 경우에는 코쉬의 적분 공식(Cauchy's integral formula)이 필수적이다.
식 (2)에 있는 통상적인 라플라스 변환은 적분이 $0$에서 시작하지만, 푸리에 변환처럼 $t$에 대한 적분 구간이 모든 실수 영역이 되게 라플라스 변환을 양방향으로 정의할 수도 있다.
 (17)
(17)식 (17)과 같은 적분 변환은 양방향 라플라스 변환(bilateral Laplace transform or two-sided Laplace transform)이라 한다. 식 (17)에 대비되는 식 (2)는 단방향 라플라스 변환(unilateral Laplace transform or one-sided Laplace transform)으로 부르기도 한다. 우리가 $t$에 대한 적분 구간을 모든 실수로 늘리기는 했지만, 양방향 라플라스 역변환(inverse bilateral Laplace transform)은 식 (6)과 동일하다. 왜냐하면 식 (10)처럼 $t$가 아닌 $s$에 대한 적분이 디랙 델타 함수를 생성하기 때문이다.
 (18)
(18) (19)
(19) (20)
(20)[참고문헌]
[1] H. Jeffreys, "Bromwich's work on operational methods," J. London Math. Soc., vol. 3, 220–223, Jul. 1930.
[2] 김계환, 김성숙, "라플라스의 생애와 현대과학에 미친 영향", 한국수학사학회지, 제32권, 제6호, pp. 271–279, 2019년 12월.
[다음 읽을거리]
 (1)
(1) (2)
(2)
 (3)
(3) (4)
(4)
 (6)
(6) (7)
(7)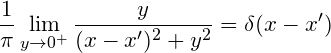
 (9)
(9)
 (10)
(10) (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16) (17)
(17) (18)
(18)
 (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4)
 (1.6a)
(1.6a) (1.6b)
(1.6b) (1.7)
(1.7)




 (1.13)
(1.13) (1.14)
(1.14)
 (1.16)
(1.16)
 (1.18)
(1.18)
 (2.1a)
(2.1a) (2.1b)
(2.1b) (2.2)
(2.2).svg/500px-Sinc_function_(both).svg.png)
 (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5)
 (2.6)
(2.6) (2.7)
(2.7)
 (2.9)
(2.9) (2.10)
(2.10) (2.11)
(2.11)






 (4.2)
(4.2)

 (4.5)
(4.5)

 (4.8)
(4.8)

 (5.2)
(5.2)


 (5.5)
(5.5) (5.6)
(5.6) (5.7)
(5.7) (5.8)
(5.8) (5.9)
(5.9) (5.10)
(5.10) (5.11)
(5.11)

 (6.3)
(6.3) (6.4)
(6.4) (6.5)
(6.5) (6.6)
(6.6)
 (7.2)
(7.2)
 (7.4)
(7.4) (7.5)
(7.5) (7.6)
(7.6) (7.7)
(7.7) (7.8)
(7.8) (7.9)
(7.9)