조금은 느리게 살자

2010년 10월 23일 토요일

페이저를 이용한 맥스웰 방정식(Maxwell's Equations Using Phasor)

[경고] 아래 글을 읽지 않고 "페이저를 이용한 맥스웰 방정식"을 보면 바보로 느껴질 수 있습니다.
1. 맥스웰 방정식
2. 전자기장 파동 방정식
3. 포텐셜 기반 파동 방정식
4. 정말 유용한 페이저 개념

[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.

페이저를 이용하면 시간에 대한 미분 방정식을 이용하지 않고 대수적으로 맥스웰 방정식을 풀 수 있다. 이때 페이저에 대한 시간 약속(time convention)을 하게 된다. 시간 약속은 두 가지 종류가 있어 이를 처음 대하는 사람들은 많이 헷갈리게 된다.

(1)

맥스웰 방정식을 시간을 중심으로 접근하는 사람들은 식 (1)에 있는 $\exp(j\omega t)$ 시간 약속을 사용한다. 식 (1)에 있는 $\omega$는 각주파수(角周波數, angular frequency)이다. 이런 시간 약속은 회로, RF(Radio Frequency) 소자, 전송선(transmission line), 도파(導波, waveguiding) 등을 연구하는 사람들이 많이 사용한다. $\exp(j\omega t)$ 시간 약속은 시간항의 위상(位相, phase)을 (+)로 정의하기 때문에 시간만 볼 때는 이 방식이 편하다.

(2)

또 다른 시간 약속은 식 (2)에 있는 $\exp(-i\omega t)$이다. $\exp(-i\omega t)$ 시간 약속은 공간을 중심으로 맥스웰 방정식을 연구하는 사람들이 사용한다. 즉, 전자파, 안테나, 산란을 연구하는 사람들은 보통 $\exp(-i\omega t)$ 시간 약속을 사용한다. 이 방식의 장점은 파동 방정식(wave equation)을 풀어봐야 이해할 수 있다. 두 가지 방식이 존재한다 해서 너무 힘들게 생각할 필요는 없다. 식 (1)과 (2)는 서로 켤레 복소수(complex conjugate)이다. 예를 들어, 식 (2)로 푼 결과에 켤레 복소수를 취하면 식 (1)로 구한 결과가 된다. 이 부분만 기억하면 참 쉽다.

먼저 다음의 맥스웰 방정식을 생각해보자.

(3: 쿨롱의 법칙)

(4: 패러데이의 법칙)

(5: 비오-사바르의 법칙)

(6: 변위전류 포함 암페어의 법칙)

식 (4)와 (6)에 있는 시간 미분을 식 (2)의 $\exp(-i\omega t)$ 시간 약속을 이용해 복소수로 바꾸어보자.

(7: 쿨롱의 법칙)

(8: 패러데이의 법칙)

(9: 비오-사바르의 법칙)

(10: 변위전류 포함 암페어의 법칙)

식 (7)에서 (10)까지의 맥스웰 방정식을 이용해 포텐셜(potential) 기반 파동 방정식을 아래와 같이 유도할 수 있다.

(11)

(12)

여기서 $k$는 파수(波數, wavenumber), $\phi$는 전기 스칼라 포텐셜(electric scalar potential), $\bar A$는 자기 벡터 포텐셜(magnetic vector potential)이다. 파수는 아래와 같이 정의한다.

(13)

식 (11)과 (12) 같은 형태로 표현되는 미분 방정식(differential equation)은 헬름홀츠 방정식(Helmholtz equation)이라 부른다. 파동 방정식의 특성으로 인해 파동의 속도 $v$는 유전율(誘電率, permittivity)과 투자율(透磁率, permeability)에만 관계된다.

(14)

여기서 $f$는 주파수(周波數, frequency), $\lambda$은 파장(波長, wavelength)이다.

[그림 1] 주파수의 개념(출처: wikipedia.org)

[그림 2] 파장의 개념(출처: wikipedia.org)

파장은 [그림 2]를 보면 쉽게 이해할 수 있다. 만약 우리가 전자파가 움직이는 모양을 사진으로 찍을 수 있다면 마치 [그림 2]처럼 정지되어 보일 것이다. 이때 동일한 모양이 반복되는 공간적인 간격을 파장이라 부른다. 쉽게 생각해 시간의 주기(temporal period)를 흔히 $T$[= $1/f$]라 정하기처럼 공간의 주기(spacial period)를 파장이라 한다고 이해하면 된다. 또한, 주파수와 파장의 개념을 이해하면 주파수 $\times$ 파장 = 속도가 되는 관계도 쉽게 보일 수 있다. 주파수는 1초 동안 동일한 행동이 반복되는 회수이며 파장은 이 동일한 행동이 발생할 때 움직인 거리이므로 이를 종합하면 1초 동안 파동이 움직인 거리가 된다. 이 비율은 당연히 속도(velocity)이다. 파수는 이해가 다소 어렵다. 파수의 단위는 rad/m이므로 이를 통해 파수 개념을 이해할 수 있다. 즉, 1 m 거리 안에 존재하는 파동의 위상수가 파수이다. 쉽게 생각하면 파수는 1 m 안에 파동이 몇 개 있는가를 표현한다. 만약 1 m에 위상수가 $2\pi$[= $360^\circ$]이면, 1 m 범위에 파동이 1개 있다.

[그림 3] 파면의 개념(출처: wikipedia.org)

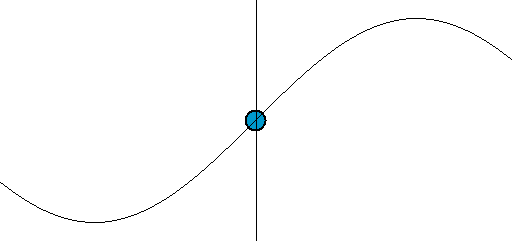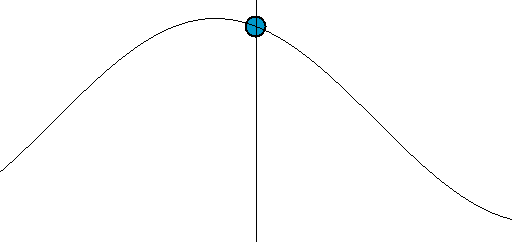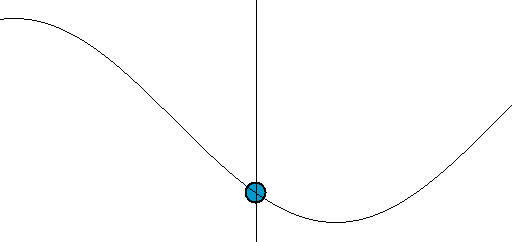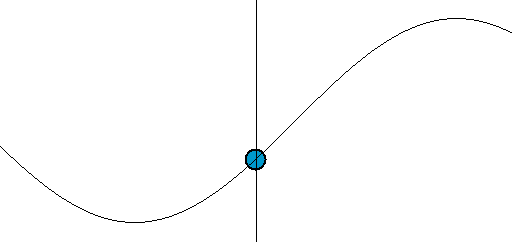
[그림 4] 파동의 움직임(출처: wikipedia.org)

방정식을 쉽게 생각하기 위해 식 (11)과 (12)에서 전하 밀도(electric charge density)와 전류 밀도(electric current density)는 0이라 생각하자. 이런 방정식은 원천이 없는 파동 방정식(sourceless wave equation)이라 한다. 이 경우 파동 방정식의 답은 무엇인가? 먼저 라플라시안(Laplacian)을 생각하자.

(15)

그러면 파동 함수(wave function) $f$는 아래로 가정할 수 있다.

(16)

식 (15)와 (16)을 원천이 없는 파동 방정식에 대입하면 다음 관계를 만족해야 한다.

(17)

식 (17)과 같이 파수와 각주파수가 이루는 관계는 분산 관계(分散關係, dispersion relation)라 한다. 물론 분산 관계의 원래 의미는 파동이 진행할 때 파동이 퍼지는[혹은 분산되는] 특성을 의미한다. 파동의 분산을 더 이론적으로 파고들려면, 주파수에 따라 파수가 변하는 관계를 알아야 한다. 그래서 파수와 주파수의 관계를 간단히 분산 관계라 할 수 있다.

[그림 3]의 빨간색 사각형이 표현하는 파면(波面, wavefront)에 기준값 개념을 적용하면 식 (16)으로 표현된 파동의 진행 방향[그림 3의 검정색 화살표]을 예측할 수 있다. 쉽게 이해하기 위해 [그림 4]를 보라. 어떻게 파동이 왼쪽에서 오른쪽으로 움직임을 인지할 수 있을까? 왜냐하면 우리가 눈으로 파면[예를 들면 꼭대기나 골짜기 등]을 추적해서 움직임을 이해하기 때문이다. 예를 들어 파면 위상의 기준값을 $0$이라 하면 $t$ = $0$일 때 $\Phi$ = $k_x x_0 + k_y y_0 + k_z z_0$ = $0$을 만족해야 한다. 이 관계를 벡터적으로 쓰면 $\bar k \cdot \bar r_0$ = $0$이 된다. 여기서 $\bar k$는 파수 벡터(wavenumber vector: 전자파가 진행하는 위상을 표현하는 벡터)이며 기준 위치 벡터는 $\bar r_0$ = $(x_0, y_0, z_0)$로 쓴다. 기준 위치 벡터는 파면 혹은 동위상 표면에 있는 임의의 점이다. 바로 얻어지는 결과중 하나를 보면 내적(inner product) 정의에 의해 파수 벡터 $\bar k$는 기준 위치 벡터 $\bar r_0$에 항상 수직이다. 3차원 공간 관점으로 보면 파수 벡터 $\bar k$는 평면의 법선 벡터가 되고 기준 위치 벡터는 평면[여기서는 파면]에 놓여 있는 임의의 점이 된다. 즉, 파수 벡터는 동위상 표면인 파면에 항상 수직이다. 다음으로 $t = \Delta t$가 되면 기준값 0을 만족하기 위해 $k_x x_1 + k_y y_1 + k_z z_1$ = $\omega \Delta t$가 되어야 한다.

(18)

여기서 $\bar r_1$ = $(x_1, y_1, z_1)$는 시간이 $t$ = $\Delta t$ 만큼 흐른 후 형성되는 평면을 표현하는 위치 벡터이다. 식 (18)에서 좌변이 $0$보다 크려면 새롭게 위치 벡터의 차이인 $\Delta \bar r$ = $\bar r_1 - \bar r_0$가 벡터 $\bar k$ 방향으로 형성되어야 한다.[∵ 내적(inner product)의 특성을 생각하라.] 이를 수식으로 표현하면 $\bar r_1$ = $\bar r_0 + \Delta \bar r$이 된다. 즉, $\bar r_1$ = $(x_1, y_1, z_1)$은 $\bar r_0$ = $(x_0, y_0, z_0)$로부터 $\bar k$ = $(k_x, k_y, k_z)$ 방향으로 $|\Delta \bar r|$ = $\omega \Delta t / k$ = $v \Delta t$ 만큼 진행한 형태가 된다. 이 개념이 헷갈리면 3차원 공간의 평면 방정식을 다시 고민해 보라. 좀더 쉬운 이해를 위해 예를 하나 들자. $\bar k$가 $z$방향인 경우 $\bar r_0$ = $(x, y, 0)$이 되어 $x$-$y$ 평면에 있는 임의의 점이 된다. 시간이 $\Delta t$ 만큼 지나면 $\Delta \bar r$ = $(0, 0, \Delta z)$가 되어 $t$ = $\Delta t$에서 $\Phi = 0$ 파면은 $\bar r_1$ = $(x, y, \Delta z)$ 위치에 있다. 이 $\bar r_1$ 위치를 $\bar r_0$ = $(x, y, 0)$과 비교하면 $z$ = $0$ 평면이 이동하여 $z$ = $\Delta z$ 평면이 됨과 동일하다. 이런 특성으로 인해 파동은 벡터 $\bar k$ 방향으로 분명히 진행한다. 그래서, 전자파의 공간적 진행을 연구하는 사람들은 $\exp(-i\omega t)$ 시간 약속을 주로 사용한다.

[다음 읽을거리]
1. 대칭적인 맥스웰 방정식
2. 침투 깊이의 이해
3. 그린 함수
4. 균일 평면파

2010년 10월 18일 월요일

정말 유용한 페이저(Phasor) 개념

[경고] 아래 글을 읽지 않고 "페이저 개념"을 보면 바보로 느껴질 수 있습니다.

1. 복소수

2. 미분법의 의미
3. 삼각 함수

[확인] 본 페이지는 exp(jωt) 시간 약속을 사용하고 있습니다.

[그림 1] 페이저의 기하학적 의미(출처: wikipedia.org)

공과대학에 입학해서 처음 배우는 수학은 미분적분학이다. 그 다음으로 미분 방정식(微分方程式, differential equation)을 배운다. 고등학교 미적분과는 너무 다른 미분 방정식 분야를 만나면, 어렵다 혹은 포기하고 싶다는 생각이 들지만 수학과도 아닌데 도대체 왜 배우지라는 마음도 가지게 된다. 이런 마음의 흔들림은 정말 당연하다. 미분 방정식은 절대로 쉽지 않다. 그럴듯한 책 제목으로 독자를 현혹하기도 하지만, 고등 학문 특히 수학에는 왕도가 없기 때문에 미분 방정식을 쉽게 배울 수 있는 방법은 진짜 없다. 미분 방정식 문제를 많이 풀어보고 미분 방정식의 수학적 기반을 고민해야 앞으로 한 걸음 나갈 수 있다. 이런 고행을 쌓고 내공을 더해가야 전문가가 될 수 있다. 특히나 공학도를 힘들게 하는 부분은 이 미분 방정식 이론이 대부분의 시스템 설계에 사용된다는 사실이다. 그래서, 미분 방정식을 배우는 공학도는 웃는 얼굴을 하기가 힘들다. 이런 상황에서 우리를 미분 방정식에서 해방시키는 놀라운 개념을 배우게 된다. 바로 페이저(phasor) 혹은 위상자(位相子) 개념이다. 페이저는 미분 방정식을 쓰지 않고 미분 방정식을 풀게 해주는 재미있는 도구이다. 페이저라는 신개념을 최초로 제안한 사람은 수학을 싫어했던 공학자 헤비사이드Oliver Heaviside(1850–1925)이다.[역설적이게도 헤비사이드의 논문은 수학식으로 도배되어 있다.] 헤비사이드와 독립적으로 페이저를 완성한 공학자는 교류 회로 이론(AC circuit theory)으로 유명한 스타인메츠Charles Steinmetz(1865–1923)이다[1]. 헤비사이드와 스타인메츠는 1893년헤비사이드 43세, 스타인메츠 28세, 조선 고종 시절에 비슷한 개념의 페이저 논문을 거의 동시에 발표했다. 다만 연산 미적분학(operational calculus)을 제안하면서 덤으로 페이저 개념을 언급한 헤비사이드의 논문 수준이 스타인메츠보다 훨씬 높다. 이런 결과는 자존심 강한 스타인메츠에게 다소 충격이었을 것이다.

헤비사이드와 스타인메츠는 누구나 알고 있는 식 (1)을 주의깊게 살펴보았다.

(1)

여기서 $j$ = $\sqrt{-1}$, $\omega$[= $2 \pi f$ = $2 \pi /T$]는 각주파수(角周波數, angular frequency)이며 $f$는 주파수(frequency)이다. 주파수[단위는 Hz]는 [그림 2]처럼 $1$초에 특정 동작이 반복되는 회수이다. 각주파수[단위는 rad/s]는 [그림 3]처럼 $1$초 동안 회전하는 각도를 라디안(radian: 아래 그림 4 참고)으로 나타낸다. 예를 들어, $1$초에 한바퀴를 돌면 $2 \pi$[= 360˚]이므로 각주파수는 $2\pi$ rad/s가 된다. 교류 회로 이론에서는 전류 $i$와 구별하기 위해 허수 단위를 $j$로 쓴다. 허수 단위를 $j$로 바꾼 제안자는 스타인메츠이다[1].

[그림 2] 주파수의 개념(출처: wikipedia.org)

[그림 3] 각주파수의 개념(출처: wikipedia.org)

[그림 4] 라디안의 정의(출처: wikipedia.org)

수학 연산을 고려하지 않고 다소 무식하게 식 (1)을 보면 $d/dt \equiv j \omega$라고 착각할 수 있다. 이런 방식이 말이 될까? 하지만 이 오해는 정말 아주 위대한 착각이다. 이 성질을 이용하여 미분 방정식 개념을 사용하지 않고 대수적으로만 미분 방정식을 풀 수 있기 때문이다. 예를 들면 식 (1)의 좌변은 미분식이지만 우변은 복소수 기반의 대수식이기 때문에 미분식을 복소수로 해결할 수 있다. 즉, 미분하기를 복소수 곱셈하기로 계산할 수 있다. 이 개념을 확장하면 AC(교류, 交流, Alternating Current) 회로 이론과 페이저 기반 맥스웰 방정식 등을 얻을 수 있다. 시간 약속 $\exp(j \omega t)$와 정반대 시간 약속은 $\exp(-i \omega t)$이다. 시간이 증가함에 따라 $\exp(j \omega t)$와 $\exp(-i \omega t)$는 복소 평면에서 서로 반대 방향으로 회전한다. 자세하게 이해하려면 파동의 시간 약속 개념이 필요하다.

미분 연산자를 숫자로 대체하는 기법은 어디서 많이 본 것 같지 않은가? 바로 그 유명한 라플라스 변환(Laplace transform)이다. 라플라스 변환은 미분 방정식을 대수적으로 해결하는 매우 유용한 방법이다.[사실 라플라스 변환은 헤비사이드가 만든 연산 미적분학(operational calculus)을 복소 함수론으로 개선한 결과물이다.] 헤비사이드가 이런 라플라스 변환을 베꼈다고 착각하지는 말라. 미분 방정식을 푸는 라플라스 변환의 창시자가 헤비사이드이다. 하지만 헤비사이드가 사용한 적분식은 대(大)수학자 라플라스Pierre-Simon Laplace(1749–1827)가 이전에 이미 제안한 식과 같았다. 그래서 새로운 적분 변환(integral transform)의 명칭을 라플라스 변환으로 붙였다. 미분 연산자의 숫자 대체 기법이 잘 이해가지 않더라도 너무 실망할 필요는 없다. 헤비사이드가 이 방법을 제안했을 때 당대 수학자들은 맹렬히 공격했다. 헤비사이드의 방법론은 수학적으로 엄밀하지 않았고 대수적으로 미분 방정식을 해결할 수 있는지도 모호했다. 당연하게도 수학자들은 자기 본성에 맞게 연산 미적분학과 라플라스 변환을 계속 의심했다. 하지만 헤비사이드는 개의치 않고 자기만의 방법을 계속 만들어갔다. 후에 브롬위치Thomas John I'Anson Bromwich(1875–1929)가 연산 미적분학의 수렴성과 라플라스 역변환(inverse Laplace transform)이 존재함을 복소 함수론(complex analysis)으로 증명하여서 라플라스 변환은 수학 이론의 반열에 들게 된다. 또 다른 측면에서 한가지 의문이 든다. 모든 시간 변화 함수를 $\exp(j \omega t)$ 형태로 표현할 수 있는가? 이런 $\exp(j \omega t)$ 접근법의 타당성은 푸리에 급수(Fourier series) 혹은 푸리에 변환(Fourier transform)과 밀접하게 관련되어 있다.

지수 함 수 $\exp(j \omega t)$를 기하학적으로 표현하면 [그림 1]처럼 된다. $\omega$는 $2 \pi \cdot f$이므로 1초에 $f$개 만큼의 한바퀴 회전[= $2 \pi$ 혹은 360˚]이 얻어진다. 이 모양을 [그림 1]이 정확하게 보여주고 있다. 또한 오일러의 공식(Euler's formula)을 사용하면 지수 함수를 삼각 함수로 바꿀 수 있다.

(2)

그래서, [그림 1]은 이 복소 지수 함수(complex exponential function)가 삼각 함수 중에서 코사인(cosine) 함수로 바뀌는 모습을 보여준다. 식 (2)에서 실수부(real part)만 택하면 다음 페이저(phasor) 관계를 정의할 수 있다.

(3)

여기서 $A$는 전압(voltage)의 진폭(amplitude), $\phi$는 전압의 위상(phase), $\Re(\cdot)$은 복소수의 실수부(real part)를 얻는 함수이다. 식 (3)에서 알파벳을 굵게 표시한 $\bf V$가 페이저가 된다. 페이저는 크기(amplitude or magnitude)와 위상(phase)으로만 구성이 되고 $\exp(j \omega t)$는 생략한다. 또한 $v(t)$를 정의하기 위해 식 (3)처럼 페이저의 실수부를 택한 부분은 큰 의미가 없다.[혹은 페이저의 허수부를 이용해 $v(t)$ = $\Im[Ae^{j(\omega t + \phi)}]$ = $A \sin(\omega t + \phi)$로 택하더라도 전혀 문제 없다.] 많은 연구자가 페이저의 실수부를 택해 시간 영역 전압을 정의하고 있으므로 식 (3)은 그냥 대세를 따랐다.

[그림 5] 페이저 합의 특성(출처: wikipedia.org)

페이저의 사칙 연산은 복소수를 이용하여 쉽게 정의할 수 있다.

(4)

(5)

(6)

식 (6)은 식 (2)를 이용하여 지수 함수를 삼각 함수로 분해한 후 크기와 위상을 구하면 증명할 수 있다. 페이저의 빼기는 식 (6) 공식과 비슷하다. 단지 $A_2 \to -A_2$로 바꾸면 빼기 공식을 쉽게 얻을 수 있다.

페이저의 유용성은 평균 AC 전력(average AC power)을 계산할 때도 나타난다. 식 (3)을 이용하여 전압과 전류 페이저를 아래로 정의하자.

(7)

(8)

전기 전력 정의 및 식 (7)과 (8)을 이용해서 평균 AC 전력을 계산하면 매우 단순화된 결과를 얻을 수 있다.

(9)

여기서 $A_v, A_i$는 전압(voltage)과 전류(electric current)의 진폭을 나타내는 실수(real number), 셋째식에 있는 $(\cdot)^*$는 켤레 복소수(complex conjugate)이다. 페이저 정의인 식 (7)과 오일러의 공식(Euler's formula)을 이용해 식 (9)의 셋째식을 다음과 같이 유도할 수 있다.

(10)

식 (9)를 보면 순시 전력(瞬時電力, instantaneous power)은 시간 변동 성분을 갖지만[∵ 시간에 따라 전압과 전류가 변하므로] 평균 전력(平均電力, average power)은 상수임을 볼 수 있다. 그래서 회로 이론의 전력 계산은 순시 전력이 아닌 평균 전력을 주로 사용하게 된다. 평균 전력의 유용성은 식 (11)에 제시한 전압과 전류의 위상차 관점에서도 생각할 수 있다.

(11)

식 (11)에 나타나는 코사인 함수는 보통 역률(力率, power factor)이라 부른다. 역률이 1이 되면[전압과 전류의 위상차가 $0$이면] 최대 평균 전력이 나타나고 역률이 $0$이면[전압과 전류의 위상차가 90˚ 혹은 270˚가 되면] 평균 전력도 $0$이 된다. 왜 이런 현상이 나타나는가 하면 식 (9)에서도 알 수 있듯이 순시 전력[= $v(t)\cdot i(t)$]을 평균하기 때문이다. 전압과 전류의 위상이 맞지 않으면, 주기동안 전력을 소모[$+$ 부호]하기도 하고 생산[$-$ 부호]하기도 한다. 따라서 전 주기에 걸쳐 순시 전력을 합한 총계는 위상이 맞지 않아 크기가 항상 줄어든다. 식 (9)와 (11)에서 평균 전력을 정의할 때는 주로 전류의 켤레 복소수를 취한다. 이는 전류 위상을 기준으로 전압 위상과의 차이를 본다는 뜻이다. 만약 전압의 켤레 복소수를 취하면 그 답은 틀릴까? 아니다. 틀리는 부분은 없다. 하지만 이런 선택은 약속이기 때문에, 전체 이론에서 언제나 일관되게 사용해야 한다. 비슷한 예를 볼 수 있는 이론은 포인팅의 정리(Poynting's theorem)이다.

추가적으로 전류의 켤레 복소수로 평균 전력을 정의한 이유를 회로 관점으로 찾는다면, 페이저 관점의 옴 법칙(Ohm's law) 때문이라 말할 수도 있다.

(12)

(13)

식 (13)에 있는 옴의 법칙으로 인해 전압 위상은 전류 위상을 기준으로 정한다. 평균 전력을 구하기 위해 식 (13)에 전류의 켤레 복소수를 곱하면 전류 위상이 약분되므로 쉽게 평균 전력을 구할 수 있다.

[그림 6] 신호의 위상차(출처: wikipedia.org)

쉽게 얘기하면, 평균 AC 전력을 정의할 때 전류의 켤레 복소수를 취한 이유는 전압과 전류 위상이 얼마나 일치하는지 찾기 위해서이다. [그림 6]의 위상차(位相差, phase difference)는 신호간의 위상[혹은 모양]이 얼마나 차이나는지 알려준다. 즉, 켤레 복소수를 취하면 전압과 전류의 위상차를 전류 위상을 기준으로 빼서 아래와 같이 계산할 수 있다. 위상차[= $\phi_v - \phi_i$]가 없는 경우가 전력을 최대로 소비할 수 있는 경우이다.

(14)

여기서 식 (14)의 실수부는 부하에서 소비되는 전력인 유효 전력(effective power or available power), 허수부는 커패시터(capacitor)나 인덕터(inductor)에 저장되는 전력인 무효 전력(reactive power)이다. 추가적으로 식 (14)의 절대값인 $A_v A_i$는 유효와 무효 전력을 모두 포함하는 피상 전력(apparent power)이 된다. 식 (14)에서 위상이 같으면[혹은 동위상(in phase), $\phi_v$ = $\phi_i$] 전력[= 전압과 전류의 곱]은 항상 양($+$)이다.[∵ 신호의 크기를 나타내는 $A_v, A_i$는 항상 양이기 때문에] 반대 위상(out of phase)이면 전압과 전류의 부호가 반대이므로 전력은 음($-$)이 된다. 전력이 음이 되면 전력을 소비하지 않고 생산한다는 뜻이다. 위상이 직교 혹은 직각 위상(quadrature phase: $\phi_v$ = $\phi_i \pm \pi/2$)이면 전력은 식 (14)의 마지막식처럼 순허수가 된다. 순허수 전력의 의미를 알려면 직교 위상 관계식[$\phi_v$ = $\phi_i \pm \pi/2$]을 식 (9)에 대입하면 된다. 페이저는 식 (3)의 정의처럼 실제 신호를 편하게 표현하기 위해 사용한다. 위상이 90˚만큼 차이나게 되면 식 (3)에서 코사인 함수는 사인 함수로 바뀐다. 즉, 평균 전력을 계산할 때는 식 (15)처럼 코사인과 사인 함수의 곱을 적분해야 한다. 최종 결과는 식 (11)에 있는 역률이다. 이 값은 분명히 $0$이므로 순허수 전력은 평균 전력에 기여할 수 없다.

(15)

물론 순허수 전력의 순시 전력이 항상 $0$은 아니다.[∵ 전류와 전압이 존재하기 때문에] 한 주기에 대해 적분한 평균 전력이 $0$이다.

[참고문헌]

[1] A. E. A. Araújo and D. A. V. Tonidandel, "Steinmetz and the concept of phasor: a forgotten story," J. Control Autom. Electr. Syst., vol. 24, pp. 388–395, 2013.

[다음 읽을거리]
1. 페이저를 이용한 맥스웰 방정식
2. 페이저를 이용한 임피던스 정의

3. 연산 미적분학

2010년 10월 17일 일요일

이항 정리(二項定理, Binomial Theorem)

[경고] 아래 글을 읽지 않고 "이항 정리"를 보면 바보로 느껴질 수 있습니다.

[그림 1] 이항 정리의 기하학적 의미(출처: wikipedia.org)

조합(組合, combination)을 활용할 수 있는 재미난 예는 이항 정리(二項定理, binomial theorem)이다. 한글로 보면 이항이 무엇인지 분명하지 않지만 한자(二項)를 보면 항이 두 개라는 뜻이다. 이항 정리는 두 항의 합[= $x+y$]에 대한 거듭제곱을 전개하여 단항식의 합으로 정리한 식을 의미한다.

[이항 정리]

(1)

[증명]

조합의 의미를 이용하면 식 (1)은 쉽게 증명할 수 있다. 서로 다른 항이 $n$개 들어있는 식[∵ $(x+y)^n$은 식 $(x+y)$가 $n$번 곱해진 식이므로]에서 변수 $x$를 $k$개 뽑아서 순서를 고려하지 않고 모은 경우의 수는 조합 ${}_nC_k$가 되므로[혹은 각각 $k$개와 $n-k$개인 구별되지 않는 변수 $x$와 $y$를 순서대로 나열하는 경우의 수는 중복을 제거해서 $n! \mathop{/}[k! (n-k)!]$이 되므로], 식 (1)이 성립한다. 더 쉽게 $(x+y)^n$을 구별되게 $(x_1 + y_1)(x_2 + y_2) \cdots (x_n + y_n)$으로 놓고, $x_1, x_2, \cdots, x_n$ 중에서 $k$를 뽑는 경우의 수는 당연히 ${}_nC_k$가 된다. 왜냐하면 분배 법칙으로 만드는 여러 $x_i$의 곱은 중복될 수 없는 같은 연산 결과이기 때문이다. 예를 들면, $x_i x_j$ 곱이 있는 상태에서 $x_j x_i$는 나올 수 없고[이미 분배해서 한 번 더 곱을 만들 수 없어서], $x_i x_j x_k$는 $x_j x_k x_i$, $x_k x_i x_j$ 등과 동일한 분배 항이다.

______________________________

식 (1)에 등장하는 조합 ${}_nC_k$는 이항 정리의 이항 계수(binomial coefficient)이며, ${}_nC_k$ = ${}_nC_{n-k}$가 성립해서 전개식의 좌우에 배치된 이항 계수는 서로 대칭이다. 이항 정리는 예전부터 잘 알려진 개념이지만, 파스칼Blaise Pascal(1623–1662)의 산술 삼각형 논고에서 조합과 파스칼의 삼각형을 이용해 이항 정리를 수학적으로 새롭게 제시했다[2]. 식 (1)의 이항 정리를 이용하면 모든 경우에 대한 멱함수(冪函數, power) 미분 공식을 유도할 수 있다.

[멱함수(power) $x^n$의 미분]

(2)

여기서 $n$은 0을 포함한 자연수(natural number)이다.

[증명]

식 (1)에서 $y$ = $\Delta x$라 두고 $\Delta x \to 0$으로 가는 극한(limit)을 취하면 식 (2)가 증명된다.

______________________________

[음의 지수를 가진 $x^{-n}$의 미분]

(3)

여기서 $n$은 자연수(自然數, natural number)이다.

[증명]

(4)
______________________________

식 (2)와 (4)를 종합하면 모든 정수 $n$에 대해 멱함수 $x^n$이 만족하는 미분 공식을 유도할 수 있다.

[유리수 지수를 가진 $x^{n/m}$의 미분]

(5)

여기서 $n, m$은 정수(整數, integer)이다.

[증명]

(6)

______________________________

식 (5)를 통해 멱함수의 미분 공식이 모든 유리수(有理數, rational number)로 확대된다.

[실수 지수를 가진 $x^r$의 미분]

(7)

여기서 $r$은 실수(實數, real number)이다.

[증명]

실수에 포함되는 무리수(無理數, irrational number)는 유리수의 극한으로 표현될 수 있으므로 정수 $n, m$의 자리수를 계속 늘려가면 식 (5)의 결과는 식 (7)에 한없이 가까이 갈 수 있다. 예를 들면, 무리수 $\sqrt{2}$ = 1.4142135623731...는 1, 14/10, 141/100, 1414/1000, 14142/10000, 등으로 오차를 한없이 줄이면서 지속적으로 유리수 근사를 할 수 있다. 하지만 유리수 근사를 할 수 있다고 해서 무리수를 유리수로 표현할 수는 없다.

______________________________

식 (7)은 미분학 시간에서 거의 처음에 배우는 미분 공식이지만 증명 자체는 매우 난해하다. 수업 시간에는 그냥 넘어가지만 꼼꼼하게 고민하면 배울 부분이 많다. 식 (7) 증명에 사용한 논리인 유리수의 자리수를 계속 늘리면 무리수가 될 수 있다는 성질은 뉴턴이 식 (7)을 증명할 때 이미 사용했다[1]. 뉴턴이 제안한 미분 공식 (7)은 분명 틀리지 않았기 때문이다. 하지만 유리수 자리수를 늘려가면 정말 무리수를 표현할 수 있을까? 무리수와 유리수는 사실 동일한 특성을 가진 수일까? 무리수를 유리수의 극한으로 표현할 수 있다는 설명을 수학적으로 잘 이해하려면 실수의 완비성(完備性, completeness)을 꼭 고민해야 한다. 데데킨트의 절단(Dedekind cut)을 이용하면 유리수는 아무리 자리수를 늘려가도 무리수가 될 수는 없다. 하지만 식 (7)의 증명에 사용한 논리처럼 유리수의 자리수를 늘려서 극한처럼 활용하면, 무리수와 무리수에 접근하는 유리수의 차이를 계속 줄일 수 있다.

식 (7)을 이용하면 뉴턴의 이항 정리(Newton's binomial theorem) 혹은 일반화 이항 정리(generalized binomial theorem)를 쉽게 증명할 수 있다[4]. 1665년뉴턴 22세, 조선 현종 시절 대학교 4학년이던 뉴턴Isaac Newton(1643–1727)이 미적분학을 만들면서 뉴턴의 이항 정리도 함께 발견했다.

[뉴턴의 이항 정리]

(8)

[증명]

식 (7)에서 유도한 멱함수의 미분 공식을 테일러 급수(級數, Taylor series)에 적용하여 $(1+x)^r$에 대한 멱급수(power series)를 생성한다.

______________________________

식 (8)에 등장하는 $(r)_k$는 포흐하머 기호(Pochhammer symbol) 혹은 하강 계승(falling factorial)이라 부른다. 하강 계승과 비슷하게 상승 계승(rising factorial)도 만든다.

(9a)

(9b)

여기서 $(x)_0$ = $1$로 정의한다. 항들의 간격까지 조정하는 포흐하머 기호의 일반화(generalization of Pochhammer symbol)도 가능하다.

(10)

여기서 $(x)_{0,h}$ = $1$, $(x)_n$ = $(x)_{n,-1}$, $x^{(n)}$ = $(x)_{n,1}$이다. 식 (10)에 있는 간격 $h$의 부호에 따라 상승이나 하강 계승이 될 수 있어서 식 (10)은 포흐하머 기호의 일반화가 분명하다. 최근에는 식 (10)을 포흐하머 $k$-기호(Pochhammer $k$-symbol)로 부르기도 한다.

뉴턴의 이항 정리에서 지수 $r$이 $0$ 혹은 자연수가 아니라면, 식 (8)은 급수의 항이 끝없이 계속 나타나는 무한 급수가 된다. 특히 일반화 이항 정리에 나오는 이항 계수를 가지고 전개한 식 (8)과 같은 무한 급수는 이항 급수(二項級數, binomial series)라고 이름 붙인다. 이 이항 급수는 $x$에 따라 발산하기도 하고 수렴하기도 한다. 식 (8)이 수렴하는 경우는 비율 판정(ratio test)을 이용하여 계산할 수 있다.

(11)

따라서 식 (8)이 무한 급수인 경우 수렴 구간은 $|x| < 1$이다.

지수 $r$이 $0$ 혹은 자연수인 경우는 조합과 순열(permutation)의 관계로 포흐하머 기호를 편하게 다룰 수 있다.

(12)

식 (1)은 다소 복잡하기 때문에, 편하게 쓸 때는 $y$ = $1$을 대입해 다음처럼 더 간략화한다.

(13)

조합 관점으로 이항 정리를 확장해서 다항 정리(多項定理, multinomial theorem)도 쉽게 획득할 수 있다.

[다항 정리]

(14)

[증명]

변수 $x_1, x_2, \cdots, x_m$를 $k_1, k_2, \cdots, k_m$개를 뽑는 경우의 수를 고려한다. 전체를 뽑아서 한 줄로 세우는 경우는 $n!$이지만, 동일한 $x_r$은 여러 번 뽑히더라도 구별이 되지 않기 때문에 $r!$로 다시 나누어야 한다. 따라서 계승 $r!$로 나누는 과정을 $k_1, k_2, \cdots, k_m$에 대해 반복하면 식 (14)가 얻어진다.

______________________________

식 (14)에서 항 $x_1^{k_1}x_2^{k_2} \cdots x_m^{k_m}$ 앞에 있는 계수는 다항 계수(multinomial coefficient)라 부른다. 거듭제곱을 $n$ = $2$로 한정하면, 다항 계수는 바로 이항 계수가 된다.

식 (1)과 (13)을 중심으로 여러 연산을 잘 적용하면 아래처럼 다양한 조합 공식을 만들어낼 수 있다.

1. 기본(basics)

[그림 1.1] 파스칼의 삼각형(출처: wikipedia.org)

[파스칼의 삼각형(Pascal's triangle)]

(1.1)

[증명]

식 (12)의 조합 정의를 통해 증명할 수 있다.

(1.2)
______________________________

파스칼의 삼각형에 수학자 파스칼Blaise Pascal(1623–1662)의 이름이 있지만, 식 (1.1)은 고대부터 잘 알려진 공식이었다. 하지만 파스칼이 1654년파스칼 31세, 조선 효종 시절에 완성하고 1655년에 출판한 유명한 산술 삼각형 논고(論考, treaties)[2]에 파스칼의 삼각형이 나오기 때문에, 식 (1.1)을 파스칼의 삼각형이라 부른다. 파스칼이 출판한 논고는 예전부터 있던 공식을 정리한 수준이 아니었다. 짧지만 심오한 이 논고에서 파스칼은 이항 정리(binomial theorem), 조합(combination), 확률(probability), 기대값(expectation or expected value) 등을 수학적으로 깔끔하게 논증하고 증명했다. 1654년에 겪은 마차 사고로 인해 파스칼이 자신의 인생을 하느님[파스칼의 종교는 천주교]에게 바치지 않았다면, 뉴턴Isaac Newton(1643–1727) 이전에 살았던 파스칼이 손쉽게 미적분학(calculus)을 발견했을 것이다.

[조합의 합]

(1.3)

[증명]

식 (13)에서 $x$ = $1$을 대입하면 식 (1.3)이 증명된다.

______________________________

식의 좌변과 우변에 서로 다른 의미를 부여해서 조합적으로 증명하는 이중 셈(double counting) 개념을 써도 식 (1.3)이 만들어진다. 모임이 0명부터 $n$명까지 허용된다면, 서로 다른 전체 모임의 수는 $2^n$이다. 왜냐하면 어떤 한 사람은 모임에 들어갈 수 있고 혹은 들어가지 않을 수 있고[선택지는 2개], 모든 사람들은 모임 참여를 독립적으로 판단하기 때문에 $2 \times 2 \times \cdots \times 2$ = $2^n$이다. 다른 관점으로 전체 $n$명으로 $k$명을 가진 모임 개수는 ${}_nC_k$이며, 실현 가능한 전체 모임 수는 $k$를 0에서 $n$까지 허용해서 모두 더하면 된다. 이중 셈 기법에서 이 두 경우는 같아야 하므로 식 (1.3)이 성립한다.

[자연수와 조합 곱의 합]

(1.4)

[증명]

식 (13)을 $x$에 대해 미분한 후 $x$ = $1$을 대입해서 유도한다.

______________________________

[자연수 제곱과 조합 곱의 합]

(1.5)

[증명]

먼저 식 (13)을 $x$에 대해 두 번 미분한다.

(1.6)

식 (1.6)에 $x$ = $1$을 대입하고 식 (1.4)의 결과를 다시 대입하면 식 (1.5)가 얻어진다.

______________________________

[파스칼의 항등식(Pascal's identity)]

(1.7)

여기서 $S_p(n)$은 다음과 같은 $p$차 거듭제곱의 합(sum of powers)이다.

(1.8)

[증명]

파스칼 항등식의 증명을 식 (1.7)의 우변부터 시작한다. 아래와 같이 두 거듭제곱의 차이를 합한 후, 식 (1)에 있는 이항 정리를 $(k+1)^{p+1}$에 대입한다.

(1.9)
______________________________

파스칼의 항등식[2], [3]은 거듭제곱의 합을 구할 때 편리하게 사용할 수 있다.

[방데르몽드의 항등식(Vandermonde's identity)]

(1.10)

[증명]

식 (1.3)처럼 이중 셈(double counting) 개념을 써서 쉽게 증명한다. 남자 $m$명, 여자 $n$명인 집단에서 $r$명으로 구성한 서로 다른 모임을 만드는 가지수는 ${}_{m+n}C_r$이다. 또 다른 측면으로 남자에서 $k$명, 여자에서 $r-k$명을 뽑아서 만드는 모임의 개수는 ${}_{m}C_k \cdot {}_{n}C_{r-k}$이다. 이때 $k$는 사람수라서 0명부터 $r$명까지 가능하다. 모든 가능한 $k$를 다 더한 값은 식 (1.10)의 우변이다. 이는 좌변과 같아야 하므로 증명이 완성된다.

______________________________

1772년방데르몽드 37세, 조선 영조 시절에 방데르몽드의 항등식을 만든 방데르몽드Alexandre-Théophile Vandermonde(1735–1796)는 방데르몽드 행렬(Vandermonde matrix)로도 유명하다.

2. 특정값(specific value)과 극한(limit)

[제곱근의 역수]

(2.1)