[경고] 아래 글을 읽지 않고 "라플라스 변환의 성질"을 보면 바보로 느껴질 수 있습니다.

[그림 1] 교류 회로 해석에 이용된 라플라스 변환(출처: wikipedia.org)
푸리에 변환(Fourier transform)의 복소 영역(complex domain) 일반화인 라플라스 변환(Laplace transform)의 다양한 성질은 푸리에 변환의 성질을 기반으로 쉽게 유도될 수 있다.
1. 기본(basics)
[정의]
 (1.1)
(1.1) (1.2)
(1.2)[선형 사상(linear mapping or linearity)]
 (1.3)
(1.3)여기서 $G(s)$는 $g(t)$의 라플라스 변환이다.
[시간 및 주파수 편이(time and frequency shifting)]
 (1.3)
(1.3)[증명]
식 (1.1)에 시간 이동된 함수를 대입한다.
 (1.4)
(1.4)주파수 이동도 식 (1.4)와 비슷하게 적분할 수 있다.
______________________________
[시간 비율 조정(time scaling)]
 (1.5)
(1.5)
 (1.6)
(1.6)
 (1.7)
(1.7)
 (1.8)
(1.8)
 (1.9)
(1.9)
 (1.10)
(1.10)
 (1.11)
(1.11)
 (1.12)
(1.12)
 (1.13)
(1.13)
결국 의심스러운 부분 없이 명확하게 식 (1.9)의 첫째식이 불연속의 경우에도 잘 성립함을 알 수 있다.
 (1.14)
(1.14)
 (1.15)
(1.15)
 (1.16)
(1.16)
여기서 라플라스 변환은 명확한 식 (1.11)을 사용하며 $s$의 실수부는 $0$보다 크다.
 (1.17)
(1.17)
 (1.18)
(1.18)
 (1.19)
(1.19)
따라서 불연속 함수의 경우에도 식 (1.17)이 잘 성립한다.
 (1.20)
(1.20)
 (1.21)
(1.21)

 (1.22)
(1.22)
여기서 $\Re[s] > 0$, $f(t)$는 주기 $T$를 가진 주기 함수이다.
 (1.23)
(1.23)
 (1.24)
(1.24)
 (2.1)
(2.1)
 (2.2)
(2.2)
여기서 $\Re[s] > -a$이다. 만약 $a > 0$이면, $F(s)$의 극점이 좌반면[$\Re[s] < 0$]에 있어서 $e^{-at}$의 최종값은 $0$이 된다. 하지만 $a < 0$이라면, 우반면[$\Re[s] > 0$]에 $F(s)$의 극점이 있어서 최종값 정리가 성립하지 않는다.
 (3.4)
(3.4)
 (3.5)
(3.5)
 (3.6)
(3.6)

 (4.5)
(4.5)
여기서 지수 함수의 수렴을 위해 $\Re[s] > 2 \sigma$로 선택하며, $t \ge 0$이라서 $u, v$의 적분 경로는 반시계 방향으로 돈다. 라플라스 변환의 수렴 조건에 의해 다음 관계도 성립한다.
 (4.6)
(4.6)
식 (4.6)을 이용해 식 (4.5)를 정리하면, $u$에 대한 피적분 함수는 $F(u) G(s-u)$가 된다.
 (4.7)
(4.7)
 (4.8)
(4.8)
함수 $f(t)$가 실수인 경우는 다음처럼 더 간략화할 수도 있다.
 (4.9)
(4.9)
예를 들어, $f(t)$ = $u(t)$, $g(t)$ = $e^{-at}$로 가정해서 파르세발의 정리를 적용한다. 먼저 식 (4.7)의 좌변은 간단히 계산된다.
 (4.10)
(4.10)
여기서 $a > 0$이다.

 (4.11)
(4.11)
 (1.5)
(1.5)여기서 $a > 0$이다.
[증명]
변수 $t$를 $at$로 치환하여 적분한다.
 (1.6)
(1.6)______________________________
[켤레 복소수(complex conjugate)와 대칭성(symmetry)]
 (1.7)
(1.7) (1.8)
(1.8)여기서 $(\cdot)^*$는 켤레 복소수, 식 (1.7)과 (1.8)은 각각 $f(t)$가 복소수 및 실수인 경우이다.
[미분(differentiation)]
 (1.9)
(1.9)여기서 $f^{(n)}(t)$는 $f(t)$의 $n$번 미분, $0^{-}$는 0보다 작은 위치에서 0으로 한없이 접근한다는 표현이다.
[증명]
라플라스 변환의 정의에 대해 부분 적분(integration by parts)을 적용한다.
 (1.10)
(1.10)여기서 $s$의 실수부는 $0$보다 크다고 가정하므로 $t$가 커질 때 $e^{-st}$는 $0$이 된다. 고계 미분에 대해서는 식 (1.9)의 첫째식을 연속적으로 적용한다. 그러면 식 (1.9)의 둘째식을 얻을 수 있다.
______________________________
식 (1.9)에서 특이한 점은 $t$ = $0$의 함수값을 $f(0^-)$로 정의한 부분이다[1]. 함수 $f(t)$가 연속인 경우는 $f(0^+)$이든 $f(0^-)$이든 같아서 문제가 되지 않는다. 하지만 $f(t)$가 $t$ = $0$에서 불연속이면 식 (1.9)처럼 $f(0^-)$로 정확히 기술해야 한다. 이런 헷갈림을 피하기 위해 $t$ = $0$ 근방의 불연속 특성까지 고려해서 라플라스 변환을 다음처럼 다시 정의한다[1].
 (1.11)
(1.11)예를 들어, 식 (1.1) 대신 식 (1.11)을 사용하면, $f(t)$ = $\delta(t)$의 라플라스 변환은 논란의 여지 없이 $1$이 될 수 있다. 왜냐하면 $t$ = $0^-$ 다음에 $t$ = $0$이 나오기 때문이다. 식 (1.1)의 정의를 이용해 $\delta(t)$를 라플라스 변환할 때는 애매한 부분이 있다. 적분의 시작점이 $t$ = $0$을 포함하는지 하지 않는지가 불분명해서 라플라스 변환이 $1$이 될 수도 $0$이 될 수도 있다.
새로운 정의인 식 (1.11)의 라플라스 변환을 쓰면, 적분은 $t$ = $0^-$에서 시작하기 때문에 식 (1.9)의 첫째식은 당연하다. 혹시라도 우리의 추론에 미심쩍은 부분이 있을 수도 있다. 그래서 단위 계단 함수(unit step function) $u(t)$를 이용해 $t$ = $0$에서 불연속인 함수 $f(t)$를 $g(t)$로 다시 정의한다.
 (1.12)
(1.12)단위 계단 함수의 성질에 의해 $u(t)$의 미분은 디랙 델타 함수(Dirac delta function) $\delta(t)$이다. 이 결과를 식 (1.11)에 대입해 정리한다.
 (1.13)
(1.13)[적분(integration)]
 (1.14)
(1.14)[증명]
식 (1.14)에 나온 적분을 식 (4.1)의 길쌈(convolution)으로 바꾸어서 식 (4.3)과 같은 라플라스 변환을 적용한다.
 (1.15)
(1.15)여기서 $u(t)$는 단위 계단 함수(unit step function)이다.
______________________________
[특수한 변환값]
 (1.16)
(1.16)[초기값 정리(initial value theorem)]
 (1.17)
(1.17)[증명]
식 (1.1)에 $s$를 곱해서 부분 적분을 한다.
 (1.18)
(1.18)식 (1.18)의 최종 결과에 $s \to \infty$를 적용하면, 적분 항은 $0$이 되므로 남는 항은 $f(0)$이다. 따라서 연속 함수인 경우는 식 (1.17)이 잘 성립한다. 만약 $t$ = $0$이라면 결과는 어떻게 될까? 함수 $f(t)$를 식 (1.12)에 있는 $g(t)$로 바꾸고 식 (1.11)을 이용해 라플라스 변환한다.
 (1.19)
(1.19)______________________________
미분의 라플라스 변환인 식 (1.9)의 첫째식과 식 (1.17)을 비교하면 $t$ = $0$에서 접근하는 $f(t)$의 극한이 좌극한 $f(0^-)$와 우극한 $f(0^+)$로 서로 다르다. 이런 애매한 부분의 해결책은 명확한 라플라스 변환인 식 (1.11)이다.
[최종값 정리(final value theorem)]
 (1.20)
(1.20)[증명]
식 (1.19)의 마지막식에 $s \to 0$ 조건을 적용해서 정리해본다.
 (1.21)
(1.21)그러면 식 (1.21)이 쉽게 증명되지만 조심할 부분도 있다. 극한 $s \to 0$ 조건에서 식 (1.21)의 결과가 $sF(s)$라는 보장이 있는가? 즉 $s \to 0$일 때, $f(t)$와 $F(s)$는 라플라스 변환 관계를 가지고 있을까? 이를 위해 식 (1.2)에 쓴 라플라스 역변환을 고려한다.

[그림 1.1] 라플라스 역변환을 위한 닫힌 경로
라플라스 변환 $F(s)$가 함수 $f(t)$로 연결되려면 [그림 1.1]에 있는 닫힌 경로 상의 복소 적분(complex integral)이 잘 정의되어야 한다. 시간 $t \to \infty$인 경우는 복소 적분의 수렴을 위해 닫힌 경로로 $c_1 + c_2$를 택한다. 여기서 $c_1$ 상의 $\Re[s]$ = $\sigma$이며 식 (1.2)에 의해 $s \to 0$일 때 $\sigma \to 0$이 된다. 그러면 닫힌 경로 안에 $F(s)$의 모든 극점이 존재해야 $f(t)$가 라플라스 역변환이 된다. 하지만 $s \to 0$인 조건에서는 $F(s)$의 극점이 닫힌 경로 안에 없을 수도 있다. 따라서 식 (1.20)이 성립하기 위해 $F(s)$의 모든 극점은 반드시 실수부가 음수인 위치에 있어야 한다.
______________________________
최종값 정리와 다르게 식 (1.17)에 있는 초기값 정리는 $s \to \infty$로 간다. 그래서 $F(s)$의 극점은 어디에 있든지 관계가 없다.
[주기 함수(periodic function)]
 (1.22)
(1.22)[증명]
주기 함수의 특성인 $f(t)$ = $f(t+T)$를 이용해 적분을 $T$로 나누어 다시 적분한다.
 (1.23)
(1.23)여기서 공비 $e^{-sT}$의 크기가 $1$보다 작기 때문에 무한 등비 급수는 수렴한다.
______________________________
[거듭제곱 함수(power function)]
 (1.24)
(1.24)여기서 $n$은 0 혹은 자연수이다.
[증명]
라플라스 함수의 정의인 식 (1.1)을 $s$에 대해 미분해서 유도한다.
______________________________
단순한 거듭제곱 함수 $t^n$의 라플라스 변환은 식 (2.1)에 따라 $1/s$를 $n$번 미분하고 부호를 $(-1)^n$으로 결정하면 된다. 이 결과는 $\nu$ = $n$인 식 (2.4)와 동일하다.
2. 초등 함수의 변환(transform of elementary functions)
[단위 계단 함수(unit step function)]
 (2.1)
(2.1)여기서 $\Re[s] > 0$이다. 라플라스 변환 $F(s)$의 극점이 $s$ = $0$에 있지만, 예외적으로 식 (1.20)의 최종값 정리가 성립한다. 즉 $\lim_{s \to 0} s F(s)$ = $1$은 $u(t)$의 최종값이다.
[지수 함수(exponential function)]
 (2.2)
(2.2)[삼각 함수(trigonometric function)]
 (2.3)
(2.3)
 (2.4)
(2.4)
 (3.1)
(3.1)
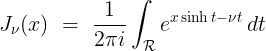 (3.2)
(3.2)
 (3.3)
(3.3)
여기서 사각형 경로상에서 $\sinh u$의 실수부는 항상 음수, 무한대에서 발산하지 않도록 $e^{-(\nu+1)u}$의 지수는 $\Re[\nu] > -1$인 조건을 가져야 한다. 식 (3.3)의 피적분 함수의 유수(residue)는 $u$ = $\sinh^{-1} s$이므로, 식 (3.3)은 유수 정리(residue theorem)를 이용해 계산한다.
 (2.3)
(2.3)여기서 $\Re[s] > 0$이다. 라플라스 변환 $F(s)$의 극점이 허수축에 있어서 최종값 정리가 성립하지 않는다.
[거듭제곱 함수(power function)]
 (2.4)
(2.4)여기서 $\Re[s] > 0$이다.
[증명]
감마 함수(gamma function)의 정의를 이용하여 식 (1.1)의 적분을 정리한다.
______________________________
3. 특수 함수의 변환(transform of special functions)
[베셀 함수(Bessel function)] [2]
 (3.1)
(3.1)여기서 $\Re[\nu] > -1$이다.
[증명]
제1종 베셀 함수를 일반적으로 정의하는 쉴레플리–좀머펠트 적분(Schläfli–Sommerfeld integral)부터 출발한다.
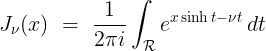 (3.2)
(3.2)여기서 $\mathcal{R}$은 복소 평면에 정의된 사각형 경로이다. 식 (3.2)의 우변에 라플라스 변환을 적용해서 정리한다.
 (3.3)
(3.3) (3.4)
(3.4)식 (3.4)에 역쌍곡 사인 함수(inverse hyperbolic sine function)의 로그 함수 표현식 $\sinh^{-1} s$ = $\log (\sqrt{s^2 + 1} + s)$를 대입해서 예쁘게 만든다.
 (3.5)
(3.5)식 (3.5)에 다시 식 (1.5)를 사용해서 증명을 완성한다.
______________________________
식 (3.5)에서 $s$ = $0$으로 놓으면 베셀 함수의 적분은 항상 1로 수렴한다.
 (3.6)
(3.6)통상적으로 베셀 함수의 정적분은 구하기 어렵지만, 라플라스 변환 관점의 적분은 조금 수월하다.
4. 길쌈(convolution)

[그림 4.1] 감쇠 지수 함수의 길쌈 예(출처: wikipedia.org)
[정의]
 (4.1)
(4.1)
 (4.2)
(4.2)
[길쌈 정리(convolution theorem)]
 (4.3)
(4.3)
 (4.4)
(4.4)
그러면 식 (4.3)의 첫째식이 증명된다. 식 (4.3)의 둘째식을 위해서는 식 (1.2)를 이용해 $f(t), g(t)$를 바꾸어 쓰면 된다.
 (4.1)
(4.1)길쌈(convolution)은 [그림 4.1]처럼 한 신호를 뒤집어서 다른 신호와 곱하기 때문에, 신호의 응답(response)을 모형화할 때 매우 유용하게 사용된다.
[대수적 성질(algebraic properties)]
 (4.2)
(4.2) (4.3)
(4.3)여기서 둘째식에 나오는 적분은 $\Re[s] > 2 \sigma$, $\sigma$는 $F(s)$와 $G(s)$의 모든 극점을 포함하도록 정하며, $u$의 적분 경로 상에서 $F(s)$와 $G(s)$는 잘 정의되며, 복소 영역으로 확장한 $u$의 적분 경로는 반시계 방향으로 설정한다.
[증명]
길쌈인 식 (4.1)의 둘째 줄을 식 (1.1)에 대입해서 차례로 정리한다.
 (4.4)
(4.4) (4.5)
(4.5) (4.6)
(4.6)______________________________
[파르세발의 정리(Parseval's theorem)]
 (4.7)
(4.7)[증명]
식 (1.7)을 식 (4.3)의 둘째식에 넣고 $s$ = $0$으로 고정해서 정리하면 식 (4.7)을 유도할 수 있다.
______________________________
식 (4.7)을 더 간단히 하기 위해 $g(t)$ = $f(t)$로 가정하면, 새로운 파르세발의 정리가 나온다.
 (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10)
[그림 4.2] 파르세발의 정리를 적용하기 위한 닫힌 경로
라플라스 변환인 $F(s)$ = $1/s$, $G(s)$ = $1/(s+a)$를 식 (4.7)의 우변에 대입해서 [그림 4.2]와 같은 복소 영역에서 적분을 한다.
 (4.11)
(4.11)여기서 극점(pole)은 $s$ = $0$과 $a$, 적분 경로 $c_1 + c_2$에 포함되는 극점은 $s$ = $0$이다.
[참고문헌]
[1] K. H. Lundberg, H. R. Miller, and D. L. Trumper, "Initial conditions, generalized functions, and the Laplace transform troubles at the origin," IEEE Control Systems Magazine, vol. 27, no. 1, pp. 22–35, Feb. 2007. (방문일 2020-10-09)
[2] "Laplace transform of Bessel function of the first kind," ProofWiki. (방문일 2023-11-12)
[다음 읽을거리]
 (1)
(1)
 (3)
(3) (4)
(4)
 (7)
(7) (8)
(8) (9)
(9)
 (11)
(11)
 (13)
(13) (15)
(15)


 (19)
(19) (20)
(20)