조금은 느리게 살자

[경고] 아래 글을 읽지 않고 "텐서 맥스웰 방정식"을 보면 바보로 느껴질 수 있습니다.
1. 텐서
2. 텐서와 좌표 변환

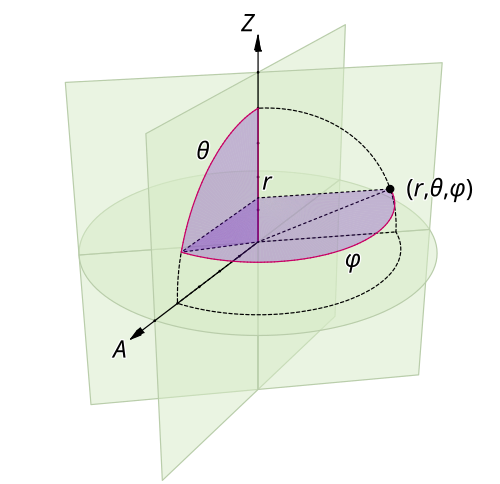
[그림 1] 일반 좌표계의 모양(출처: wikipedia.org)

좌표 불변성(coordinate independent or coordinate invariant)을 특징으로 하는 텐서(tensor)를 이용하면 맥스웰 방정식(Maxwell's equations)을 임의의 좌표계에서 기술할 수 있다. 상식적으로 생각해도 전기(electricity)와 자기(magnetism)의 특성을 기술하는 맥스웰 방정식은 좌표계 선택과는 관계없이 성립할 것 같다. 왜냐하면 좌표계는 우리가 편미분 방정식을 쓰기 위해 도입한 선택적인 개념이기 때문이다. 이런 상식을 수학적으로 절묘하면서도 아름답게 표현한 기법이 텐서 이론이다. 먼저 벡터 함수(vector function)를 표현하기 위해 공변 벡터(共變, covariant vector)와 반변 벡터(反變, contravariant vector)를 정의하자.

(1: 공변 벡터)

(2: 반변 벡터)

벡터 함수 $F$는 텐서 이론을 이용하여 [그림 1]과 같은 일반 좌표계(generalized or curvilinear coordinate system) $U$에서 정의할 수 있다.

(3)

여기서 $f^i, f_i$는 각각 공변과 반변 벡터가 기저 벡터(basis vector)인 경우의 좌표값이다. 텐서 미적분학(tensor calculus)에서 도입한 공변 도함수(covariant derivative)를 이용하면 반변 벡터와 공변 벡터를 미분할 수 있다.

(4: 반변 벡터의 공변 도함수)

(5: 공변 벡터의 공변 도함수)

텐서에서는 델(del) 혹은 나블라(nabla) 연산자를 새롭게 정의한다.

(6)

새롭게 정의한 식 (6)을 아래의 맥스웰 방정식에 대입하자.

(7: 쿨롱의 법칙)

(8: 패러데이의 법칙)

(9: 비오–사바르의 법칙)

(10: 변위 전류 포함 암페어의 법칙)

여기서 $\bar M$은 자류 밀도(magnetic current density)이다. 그러면 공변 도함수를 이용해 발산과 회전 연산자를 일반 좌표계에 적용한 맥스웰 방정식을 얻을 수 있다.

(11)

여기서 $\varepsilon_{ijk}$는 레비-치비타 기호(Levi-Civita symbol)이며 $\mathcal{G}$는 계량 텐서(metric tensor)의 행렬식(determinant)이다. 텐서 미적분학에서 소개한 복잡한 계산을 이용하면 식 (11)은 아래의 텐서 기반 맥스웰 방정식(tensor based Maxwell's equations)으로 변환할 수 있다.

(12)

(13)

(14)

(15)

위의 텐서 기반 맥스웰 방정식에서 공변 벡터와 반변 벡터가 섞여있음을 눈여겨 봐야 한다. 만약 공변 벡터와 반변 벡터를 상호 교환하려면 아래 식을 사용하면 된다.

(16)

식 (12)에서 (15)는 다소 복잡해 보이지만 좌표계에 관계없이 성립하는 가장 일반화된 맥스웰 방정식이다.

[다음 읽을거리]
1. 변환 전자기학

[경고] 아래 글을 읽지 않고 "구 좌표계"를 보면 바보로 느껴질 수 있습니다.

1. 구의 방정식

2. 텐서 미적분학

3. 직교 좌표계 텐서 미적분학

[그림 1] 구 좌표계의 표현(출처: wikipedia.org)

[그림 1, 2]의 구 좌표계 혹은 구면 좌표계(球座標系, spherical coordinate system)는 직교 좌표계(orthogonal coordinate system) 중에서도 상당히 난해한 좌표계에 속한다.

[그림 2] 구 좌표계값의 변화 모습(출처: wikipedia.org)

[그림 1]의 좌표계 구성으로 인해 데카르트 좌표계 $X$에서 구 좌표계 $U$로 가는 좌표 변환(coordinate transform)은 아래와 같다.

(1)

식 (1)은 [그림 3]과 삼각 함수(trigonometric function)를 이용해 쉽게 유도할 수 있다. 구 좌표계에서 $z$축은 극축(pole axis)이라 부른다. 극축은 좌표에 특이점이 발생하는 좌표축이다. 구 좌표 $(r, \theta, \phi)$는 3차원 상의 대부분 점을 잘 표현할 수 있지만, 극축에 있는 점에서는 문제가 생긴다. 예를 들어, $\theta$ = $0^\circ$에 두면 항상 $(x, y)$ = $(0, 0)$이다. 그러면 방위각 $\phi$는 어떤 각도든지 가능해서 3차원의 위치 벡터 $\bar r$과 구 좌표 $(r, \theta, \phi)$는 일대일 대응이 되지 않는다. 이 원인으로 인해 구 좌표로 물체를 회전시킬 때 짐벌 잠금(gimbal lock)이 출현할 수 있다.

[그림 3] 데카르트 좌표계와 구 좌표계의 상호 변환(출처: wikipedia.org)

식 (2)의 계량 텐서(metric tensor)와 관련된 척도 인자(尺度因子, scale factor) $h_i$는 식 (3)처럼 계산된다.

(2)

(3)

식 (1)을 식 (3)에 대입해 계산하면 구 좌표계의 척도 인자를 얻을 수 있다.

(4)

식 (4)를 직교 좌표계에 대한 벡터 연산자 공식에 대입한다.

(5)

(6)

(7)

(8)

그러면, 구 좌표계에 대한 벡터 연산자를 모두 정의할 수 있다.

(9)

(10)

(11)

(12a)

(12b)

다음으로 구 좌표계를 구성하는 단위 벡터(unit vector)를 데카르트 좌표계 관점으로 계산한다.

(13)

식 (13)의 첫째식을 이용하면 위치 벡터(position vector)는 $\bar P$ = $r \hat r$ = $(x, y, z)$로 간단하게 표현된다. 또한 식 (13)처럼 단위 벡터 $\rho, \theta, \phi$는 극고도각(極高度角, polar angle: $\theta$는 꼭대기부터 시작해 내려오기 때문에 일반 고도각과는 정의가 약간 다름) $\theta$와 방위각(方位角, azimuth) $\phi$에 따라 변한다. 따라서 단위 벡터 $\rho, \theta, \phi$를 미분할 때는 극고도각과 방위각의 변화율을 반드시 고려해야 한다.

(14)

여기서 단위 벡터는 $r$이 아닌 $\theta, \phi$만의 함수[$\partial \hat r / \partial r$ = $\partial \hat \theta / \partial r$ = $\partial \hat \phi / \partial r$ = $0$], $t$는 임의의 매개변수이다. 식 (14)의 증명에는 아래에 있는 원통 좌표계 단위 벡터를 사용한다.

(15)

여기서 $\hat \rho$ = $\sin \theta \hat r + \cos \theta \hat \theta$, $\hat z$ = $\cos \theta \hat r - \sin \theta \hat \theta$이다. 식 (13)을 이용하면 데카르트 좌표계를 구 좌표계로 바꾸어주는 공식을 행렬(matrix) 형태로 만들 수 있다.

(16)

식 (16)에서 행렬 ${\bf T}_{sr}$과 ${\bf T}_{rs}$가 서로 전치 행렬(transpose) 관계임은 상당히 재미있다.

[그림 4] 데카르트 좌표계의 방향 코사인 각도 $\alpha, \beta, \gamma$(출처: wikipedia.org)

구 좌표계의 반지름 단위 벡터 $\hat r$을 나타내는 관계식 (13)은 방향 코사인(direction cosine)로 좀더 쉽게 공식화할 수 있다.

(17)

여기서 $\gamma$ = $\theta$, $\cos \alpha, \cos \beta, \cos \gamma$는 각각 $x, y, z$축에 대한 방향 코사인이다.

매우 간단하고 거칠게 보면, 텐서(tensor)는 그냥 편리한 표기법이라서 식 (9)–(12)를 구 좌표계에 대한 완전 미분(exact differential)을 적용해서도 증명할 수 있다. 먼저 데카르트 좌표계의 편미분과 단위 벡터를 구 좌표계로 공식화한다.

(18)

(19)

(20)

여기서 $\rho$ = $r \sin \theta$이다. 다음 단계로 식 (16)을 써서 데카르트 좌표계의 단위 벡터를 구 좌표계의 단위 벡터로 나타낸다.

(21)

식 (18)–(21)을 데카르트 좌표계에서 정의한 식 (22)의 구배 연산자에 대입해서 기준 좌표계를 식 (9)처럼 구 좌표계로 완전히 바꾼다.

(22)

유도의 시작은 스칼라 함수 $f$의 편미분 구하기이다.

(23a)

(23b)

그 다음에 식 (23)에 식 (21)을 각각 곱하고 구 좌표계의 단위 벡터 $\hat r, \hat \theta, \hat \phi$에 대해 정리해서 명료하게 식 (9)를 얻는다. 예를 들어, 최종 결과로 획득한 $\hat r$의 성분은 식 (9)의 첫째항과 동일하다.

(24)

구 좌표계의 발산 연산자를 도출할 때는 신경을 더 써야 한다. 언제나 출발점은 데카르트 좌표계이고 완전 미분을 통해 구 좌표계로 변환한다. 우리가 계속해서 사용하고 있는 완전 미분은 텐서 이론에서도 약방의 감초처럼 엄청 많이 사용된다. 우선 처음 단계에서는 식 (16)을 사용해서 벡터 함수 $\bar F$ = $(F_x, F_y, F_z)$의 각 성분을 구 좌표계의 성분으로 표현한다.