[경고] 아래 글을 읽지 않고 "구 좌표계"를 보면 바보로 느껴질 수 있습니다.
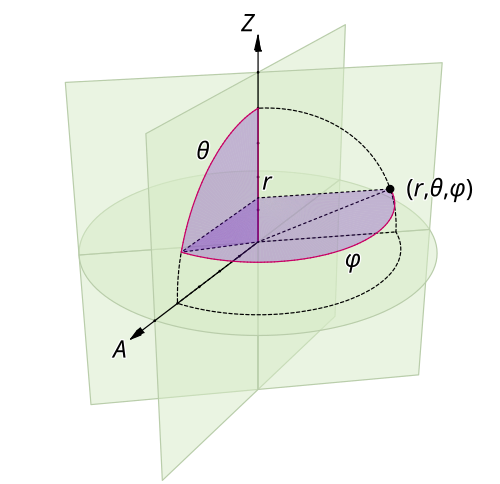

[그림 1] 구 좌표계의 표현(출처: wikipedia.org)
[그림 1, 2]의 구 좌표계 혹은 구면 좌표계(球座標系, spherical coordinate system)는 직교 좌표계(orthogonal coordinate system) 중에서도 상당히 난해한 좌표계에 속한다.
[그림 2] 구 좌표계값의 변화 모습(출처: wikipedia.org)
 (1)
(1)
식 (1)은 [그림 3]과 삼각 함수(trigonometric function)를 이용해 쉽게 유도할 수 있다. 구 좌표계에서 $z$축은 극축(pole axis)이라 부른다. 극축은 좌표에 특이점이 발생하는 좌표축이다. 구 좌표 $(r, \theta, \phi)$는 3차원 상의 대부분 점을 잘 표현할 수 있지만, 극축에 있는 점에서는 문제가 생긴다. 예를 들어, $\theta$ = $0^\circ$에 두면 항상 $(x, y)$ = $(0, 0)$이다. 그러면 방위각 $\phi$는 어떤 각도든지 가능해서 3차원의 위치 벡터 $\bar r$과 구 좌표 $(r, \theta, \phi)$는 일대일 대응이 되지 않는다. 이 원인으로 인해 구 좌표로 물체를 회전시킬 때 짐벌 잠금(gimbal lock)이 출현할 수 있다.
[그림 3] 데카르트 좌표계와 구 좌표계의 상호 변환(출처: wikipedia.org)
 (2)
(2) (3)
(3)
식 (1)을 식 (3)에 대입해 계산하면 구 좌표계의 척도 인자를 얻을 수 있다.
 (4)
(4)
식 (4)를 직교 좌표계에 대한 벡터 연산자 공식에 대입한다.
 (5)
(5) (6)
(6) (7)
(7) (8)
(8)
그러면, 구 좌표계에 대한 벡터 연산자를 모두 정의할 수 있다.
 (9)
(9) (10)
(10) (11)
(11) (12a)
(12a) (12b)
(12b)
식 (13)의 첫째식을 이용하면 위치 벡터(position vector)는 $\bar P$ = $r \hat r$ = $(x, y, z)$로 간단하게 표현된다. 또한 식 (13)처럼 단위 벡터 $\rho, \theta, \phi$는 극고도각(極高度角, polar angle: $\theta$는 꼭대기부터 시작해 내려오기 때문에 일반 고도각과는 정의가 약간 다름) $\theta$와 방위각(方位角, azimuth) $\phi$에 따라 변한다. 따라서 단위 벡터 $\rho, \theta, \phi$를 미분할 때는 극고도각과 방위각의 변화율을 반드시 고려해야 한다.
 (14)
(14)여기서 단위 벡터는 $r$이 아닌 $\theta, \phi$만의 함수[$\partial \hat r / \partial r$ = $\partial \hat \theta / \partial r$ = $\partial \hat \phi / \partial r$ = $0$], $t$는 임의의 매개변수이다. 식 (14)의 증명에는 아래에 있는 원통 좌표계 단위 벡터를 사용한다.
 (15)
(15)여기서 $\hat \rho$ = $\sin \theta \hat r + \cos \theta \hat \theta$, $\hat z$ = $\cos \theta \hat r - \sin \theta \hat \theta$이다. 식 (13)을 이용하면 데카르트 좌표계를 구 좌표계로 바꾸어주는 공식을 행렬(matrix) 형태로 만들 수 있다.
 (16)
(16)
식 (16)에서 행렬 ${\bf T}_{sr}$과 ${\bf T}_{rs}$가 서로 전치 행렬(transpose) 관계임은 상당히 재미있다.

[그림 4] 데카르트 좌표계의 방향 코사인 각도 $\alpha, \beta, \gamma$(출처: wikipedia.org)
구 좌표계의 반지름 단위 벡터 $\hat r$을 나타내는 관계식 (13)은 방향 코사인(direction cosine)로 좀더 쉽게 공식화할 수 있다.
 (17)
(17)여기서 $\gamma$ = $\theta$, $\cos \alpha, \cos \beta, \cos \gamma$는 각각 $x, y, z$축에 대한 방향 코사인이다.
매우 간단하고 거칠게 보면, 텐서(tensor)는 그냥 편리한 표기법이라서 식 (9)–(12)를 구 좌표계에 대한 완전 미분(exact differential)을 적용해서도 증명할 수 있다. 먼저 데카르트 좌표계의 편미분과 단위 벡터를 구 좌표계로 공식화한다.
 (18)
(18) (19)
(19) (20)
(20)여기서 $\rho$ = $r \sin \theta$이다. 다음 단계로 식 (16)을 써서 데카르트 좌표계의 단위 벡터를 구 좌표계의 단위 벡터로 나타낸다.
 (21)
(21)식 (18)–(21)을 데카르트 좌표계에서 정의한 식 (22)의 구배 연산자에 대입해서 기준 좌표계를 식 (9)처럼 구 좌표계로 완전히 바꾼다.
 (22)
(22)유도의 시작은 스칼라 함수 $f$의 편미분 구하기이다.
 (23a)
(23a) (23b)
(23b)그 다음에 식 (23)에 식 (21)을 각각 곱하고 구 좌표계의 단위 벡터 $\hat r, \hat \theta, \hat \phi$에 대해 정리해서 명료하게 식 (9)를 얻는다. 예를 들어, 최종 결과로 획득한 $\hat r$의 성분은 식 (9)의 첫째항과 동일하다.
 (24)
(24)구 좌표계의 발산 연산자를 도출할 때는 신경을 더 써야 한다. 언제나 출발점은 데카르트 좌표계이고 완전 미분을 통해 구 좌표계로 변환한다. 우리가 계속해서 사용하고 있는 완전 미분은 텐서 이론에서도 약방의 감초처럼 엄청 많이 사용된다. 우선 처음 단계에서는 식 (16)을 사용해서 벡터 함수 $\bar F$ = $(F_x, F_y, F_z)$의 각 성분을 구 좌표계의 성분으로 표현한다.
 (25)
(25)그 다음에 식 (23)과 비슷하게 각 성분의 편미분을 일일이 공식화한다.
 (26a)
(26a) (26b)
(26b) (26c)
(26c)마지막으로 식 (27)에 따라 식 (26)을 모두 더해서 구 좌표계의 발산 연산자인 식 (10)을 새롭게 정의한다.
 (27)
(27)예를 들면, $\partial / \partial \theta$를 가진 항을 모두 모은 결과는 다음과 같다.
 (28a)
(28a) (28b)
(28b) (28)
(28)다른 편미분인 $\partial / \partial r$과 $\partial / \partial \phi$도 유사하게 계산해서 각 항들을 깔끔하게 정리한다.
 (29)
(29) (30)
(30)최종적으로 식 (28)–(30)을 모두 합해서 식 (10)을 만들어낸다.
 (31)
(31)지금까지 보여준 과정은 단순한 편미분을 반복적으로 적용해서도 식 (10)이 나온다는 관점을 소개한다. 다만 자기 확신을 위한 연습은 한 번으로 족하다. 이후에는 텐서 이론을 이용해서 우리 개념을 수학적으로 확장해본다.
[다음 읽을거리]



감사합니다 큰도움이 되었습니다!
답글삭제언제든 놀러오세요. ^^
삭제감사합니다. 은인님
답글삭제은인님 ?? 칭찬 감사합니다.
삭제텐서부터 여기까지 쭉봤는데 궁금한게 있습니다. 구좌표에서 위치벡터를 r=rr^ 로만 쓰는데 이게 원점이 각에 무관해서 그런건가요? 그림을봐도 그렇고 책에도 이렇게 쓴다고만 나와서 그냥 그렇구나 했는데 무슨 수학적인 이유같은게 있나해서요. 그리고 위치벡터미분 dr을 보면 앞에 척도인자가 곱해지잖아요. 이게 d(rr^)하면 그냥 나오는걸로만 알고있었는데 여기 텐서에 올라온 내용보면 위치벡터 미분을 공변,반변벡터로 dr=a^idu_i 이런식으로 정의되는데 이게 보다 일반적이니까 이식에서 직교좌표에서 앞에 척도인자가 곱해지는 모양을 유도할 수 있나요? 자꾸 질문드려 죄송합니다.
답글삭제별 말씀을 다 하시네요! 서로 질문하면서 배워가는 거지요.
답글삭제1. 위치벡터는 P = (x, y, z) - (0, 0, 0)으로 정의하므로 이 정의에 식 (13)을 대입하면 말씀하신 구좌표계의 위치벡터를 얻을 수 있습니다.
2. 구좌표계에 대한 미분 연산자는 완전미분을 사용해도 쉽지만 복잡하게(?) 증명됩니다. 하지만 텐서이론과의 연결고리를 만들면 식 (13)은 거의 자동으로 유도됩니다. 이해를 돕기 위해 아래 문서에서 식 (20)을 보면 바로 이해될 것입니다.
http://ghebook.blogspot.kr/2011/07/tensor-calculus-for-orthogonal-systems.html
매번 답변해 주셔서 감사합니다. 위치벡터는 말씀대로 정말 그냥 대입하니까 rr^만 남고 다 지워지네요. 그리고 (13)번식을 잘 보니까 반변벡터를 단위벡터로 정의한것이네요.그렇게 하면 위치벡터 미분앞에 척도인자가 곱해지는 모양이 되는군요.
삭제언제든 놀러오세요. ^^
삭제으어어 외계어다 외계어.
답글삭제제가 알기로는 Tsr 과 Trs는 전치행렬로 나오는 것이 아니라 서로 같게 나오는 Tsr =Trs 로 나와야 합니다. 또한 이행렬은 자기 스스로가 역행렬인걸로 알고 잇습니다. 딱봐도 Tsr 과Tsr의 곱이 단위행렬로 안나오네요.. 수정바랍니다.
답글삭제식 (16)에 있는 행렬은 직교 행렬(orthogonal matrix)이라서, 전치 행렬 = 역행렬이 되는 것이 맞습니다, 익명님. 현재로는 고칠 부분이 없네요. ^^
삭제글 잘 일고 많은 생각에 도움이 되었습니다.하지만 너무 어렵네요. 혹시 원기둥 좌표계에서처럼 구좌표계에서도 발산식 유도과정죰 보여주실수 있나요.. 너무 어렵네요.
답글삭제그게 귀찮아서 텐서 연산을 도입한 것이라...
삭제번거로운 계산이 기다리고 있지만, 원통 좌표계와 동일한 과정을 따라가면 됩니다. 시간될 때 한 번 해보도록 할게요.
감사합니다. 다시한번 해보도록하겠습니다.
삭제안녕하세요. 전자과 재학중인 학생인데 전자기학 공부중에 블로그를 방문하게되었고 이렇게 문의 드려도 될런지요. 블로그 댓글에는 파일첨부가 안되네요
답글삭제첨부하고 싶던 파일의 내용을 이러합니다
구면좌표계에서의 표면벡터를 구하는 문제인데 이때 풀이에서는 미소면적 벡터를 구하고 그 벡터를 적분하더군요.
그런데 이때 S = int dA a_r (dA는 구면좌표계의 미소면적벡터)로 하는데 이것이 옳은 방법인가요?
원통좌표계나 구 좌표계에서 (r phi z), (r theta Phi)의 벡터를 단위벡터로 사용할때는 단위벡타 r 이 phi와 theta의 값이 바뀜에 따라 계속 변하는데 풀이는 이를 생각하지 않고 푼것으로 생각이 됩니다. 이렇게 푸는 것이 옳은 것인지 잘 모르겠습니다.
그리고 면벡터를 정의할때는 어떤 곡면에 대하여 수직인 벡터라 하고 곡면에 수직인 경우는 어떤 점에서 접평면을 만들고 그 평면에서의 법선벡터를 면벡터로 하잖아요. 이런생각을 문제로 가져가면 뭔가 이상합니다.
문제에 대한 풀이를 보면 미소면적을 적분하여 면적벡터를 구하는것으로 나와있는데 그러면 곡면의 어느지점에서 수직인지고 불명확한데 이렇게 면적소의 성분을 적분하는 것이 옳은 것인지 잘 모르겠습니다.
구 좌표계는 직교 좌표계이기 때문에 단위 벡터 2개는 나머지 단위 벡터와 반드시 직교합니다. 이런 성질을 이용해 적분한다면 말씀하신 내용이 다 맞습니다.
삭제해설의 풀이가 잘못된건가요??
답글삭제풀이가 잘못되지 않았어요. 계속 읽어보시길 바래요. ^^
삭제와... 나비에스토크스 방정식을 공부하다. 이해도 연습도 어려운 난해한 부분에 대해 수권의 책을 읽었던 시간보다 여기에 쓰신 글을 읽는 시간이 훨씬 유용했습니다.. 새롭게 공학도에 입문한 후배가 선배분의 설명에 대해 매우 감사를 표합니다. 연수원 들어가기전에 백터와 텐사에 대한 개념을 이해하고 싶었는데 다이아몬드 광산을 찾은 기분이군요.
답글삭제Iglesia님, 자주 놀러오세요. 그리고 대단하시네요. 나비에-스토크스 방정식은 저도 한 번 공부해보고 싶어요.
삭제혹시 단위 벡터 미분에서 r(단위 벡터)를 파이로 미분 할때 왜 세타(단위벡터) 가 나오는 지 식으로 알 수 있을까요.
답글삭제밑에 친구들도 그 원리들을 알고싶습니다..
빠른 답변 주시면 감사드리겠습니다 ㅠㅠㅠㅠㅠ
삭제Unknown님, 식 (13)을 보세요. 첫째식을 $\theta$에 대해 편미분하면 둘째식이 나옵니다.
삭제