[경고] 아래 글을 읽지 않고 "멜린 변환"을 보면 바보로 느껴질 수 있습니다.
약간 생소한 이름을 가진 멜린 변환(Mellin transform)은 유명한 라플라스 변환(Laplace transform)과 매우 비슷한 모양을 가지고 있다. 두 적분 변환의 유사성을 확인하기 위해, 식 (1), (2)에 제시한 멜린 변환 및 역변환을 식 (3), (4)에 있는 라플라스 변환 및 역변환과 비교한다.
 (1)
(1) (2)
(2) (3)
(3) (4)
(4)멜린 변환과 라플라스 변환의 관계를 만들 때는 양방향 라플라스 변환(bilateral Laplace transform)이 편하다.
 (5)
(5) (6)
(6)식 (5)에서 $u$ = $e^{-t}$로 변수 치환해서 정리하면 멜린 변환인 식 (1)을 얻을 수 있다.
 (7)
(7)마찬가지로 브롬위치 적분(Bromwich integral)인 식 (6)을 변수 치환해서 멜린 역변환인 식 (2)를 매우 쉽게 유도한다.
 (8)
(8)따라서 멜린 변환과 양방향 라플라스 변환의 관계를 정리하면 다음과 같다.
 (9)
(9)또한 양방향 라플라스 변환의 수렴 특성이 멜린 변환에 그대로 적용되므로, 멜린 변환이 존재하는 $s$의 범위 $\sigma_1 < \Re[s] < \sigma_2$는 보통 띠(strip) 형태를 이룬다. 그래서 수렴하는 $s$의 정의역을 기본대(基本帶, fundamental strip) 혹은 정의대(定義帶, strip of definition)로 부른다.
멜린 변환의 발견에는 다양한 수학자가 기여했다. 적분 변환을 이용해 미분 방정식을 푼다는 개념을 처음 제안한 라플라스Pierre-Simon Laplace(1749–1827)가 1785년라플라스 36세, 조선 정조 시절에 사용한 적분 변환은 멜린 변환과 유사했다. 라플라스가 도입한 적분 변환 개념은 헤비사이드Oliver Heaviside(1850–1925)와 브롬위치Thomas John I'Anson Bromwich(1875–1929)에 의해 라플라스 변환으로 완성된다. 리만Bernhard Riemann(1826–1866)은 1859년리만 33세, 조선 철종 시절에 솟수 정리(素數 定理, prime number theorem)를 고민하며 멜린 변환을 최초로 사용했다.[1989년부터 시행된 한글맞춤법에 따르면 소수(素數, prime number)로 해야 타당하나, 소수(小數, decimal fraction)와 구별되지 않으므로 옛날 표기인 솟수를 고집한다.] 그뒤 1894년카엥 29세, 조선 고종 시절에 카엥Eugène Cahen(1865–1941)이 적분 변환 개념의 멜린 변환을 다시 도입하고, 1896년멜린 42세, 조선 고종 시절에는 멜린Hjalmar Mellin(1854–1933)이 멜린 변환과 역변환을 정확히 정의하였다.

[그림 1] 멜린 역변환을 위한 닫힌 경로
멜린 역변환은 양방향 라플라스 역변환을 이용해서 충분히 증명이 가능하지만, 멜린 역변환 자체의 특성을 이해하기 위해 복소 함수론(complex analysis)으로 증명할 수도 있다. 먼저 식 (2)에 식 (1)을 대입해서 정리한다.
 (10)
(10)여기서 $\sigma$는 $(t'/t)^s$를 발산시키지 않기 위해 $0$에 매우 근접한 값으로 정한다. 식 (10)에 있는 복소 적분을 세심하게 본다. 만약 $t' > t$이면 $t'/t > 1$이므로, $R \to \infty$로 두고 [그림 1]의 닫힌 경로 $c_1 + c_3$을 따라 적분한다. [그림 1]에서 닫힌 경로 내부는 극점(pole)이나 가지 자름(branch cut)이 없어서 해석적이다. 따라서 코쉬의 적분 정리에 의해 식 (10) 내부에 있는 경로 적분(contour integral)은 $0$이 된다. 마찬가지로 $t' < t$인 경우는 닫힌 경로 $c_4 + c_6$을 따라 적분해서 식 (10) 내부의 경로 적분이 $0$임을 확인한다. 다음으로 우리가 집중적으로 봐야 하는 부분은 $t' \approx t$일 때의 경로 적분이다. 식 (10)을 바탕으로 다음 복소 적분을 도입한다.
 (11)
(11)여기서 $\Delta$는 매우 작은 양의 실수이다. 식 (11)의 첫번째와 두번째 피적분 함수는 각각 $t' > t$, $t' < t$인 조건을 만족한다. 그래서 [그림 1]에 따라 식 (11)을 닫힌 경로 적분으로 바꾼다.
 (12)
(12)여기서 $c_1$과 $c_4$를 위한 $\sigma$는 각각 $0^-$와 $0^+$이다. 식 (12)에 의해 우리가 아무리 작은 $\Delta$를 선택해도 항상 적분값은 $t$이다. 따라서 식 (11)에 나온 적분을 디랙 델타 함수(Dirac delta function)로 표현한다.
 (13)
(13)식 (13)을 식 (10)에 대입하면 최종 적분값은 $f(t)$가 나온다. 그러므로 식 (2)는 멜린 역변환이 분명하다.
함수 $f(t)$를 표현한 식 (10)과 유사하게 $F(s)$에 대해서도 멜린 변환과 역변환을 함께 적용할 수 있다. 이를 위해 식 (2)를 식 (1)에 대입해서 다음 적분을 얻는다.
 (14)
(14)식 (14)에 나온 거듭제곱 함수 $t^{s-u-1}$에 대한 적분을 더 세밀하게 계산한다.
 (15)
(15)여기서 $\Re[s]$ = $\sigma$이다. 만약 $\Re[s]$ $\ne$ $\sigma$라면, $t'$에 대한 식 (15)의 피적분 함수는 양 혹은 음의 무한대에서 발산한다. 그래서 $\sigma$는 반드시 $s$의 실수부로 택해야 한다. 식 (15)의 결과에 따라 식 (14)는 정확히 $F(s)$가 된다. 따라서 멜린 역변환 후에 멜린 변환을 하면 $F(s)$가 나와서 멜린 변환과 역변환 관계가 잘 성립함을 알 수 있다.
1. 기본(basics)
[선형 사상(linear mapping or linearity)]
 (1.1)
(1.1)여기서 $G(s)$는 $g(t)$의 멜린 변환이다.
[주파수 이동(time and frequency shifting)]
 (1.2)
(1.2)[시간 비율 조정(time scaling)]
 (1.3)
(1.3)
 (1.4)
(1.4)
 (1.6)
(1.6)
 (1.7)
(1.7)
 (1.8)
(1.8)
여기서 $(x)_n$은 포흐하머 기호(Pochhammer symbol)이다.
 (1.9)
(1.9)
 (1.10)
(1.10)
 (1.11)
(1.11)
 (1.12)
(1.12)
 (1.14)
(1.14)
 (1.15)
(1.15)
 (2.1)
(2.1)
여기서 $\Re[s] < 0$이다.
 (2.2)
(2.2)
 (1.3)
(1.3)여기서 $a > 0$이다.
[증명]
변수 $t$를 $at$로 치환하여 적분한다.
 (1.4)
(1.4)______________________________
멜린 변환에서는 시간 비율을 아무리 조정해도 멜린 변환된 함수의 전체 모양은 변하지 않는다. 다만 시간 비율을 바꾼 정도에 따라 멜린 변환의 전체 모양이 커지거나 작아질 수는 있다.
[켤레 복소수(complex conjugate)와 대칭성(symmetry)]
 (1.6)
(1.6) (1.7)
(1.7)여기서 $(\cdot)^*$는 켤레 복소수, 식 (1.6)과 (1.7)은 각각 $f(t)$가 복소수 및 실수인 경우이다.
[미분(differentiation)]
 (1.8)
(1.8)[증명]
미분된 함수를 멜린 변환의 정의에 넣고 부분 적분(integration by parts)을 적용한다.
 (1.9)
(1.9)고계 미분에 대해서는 식 (1.8)의 첫째식을 연속적으로 $n$번 적용한다. 그러면 식 (1.8)의 둘째식이 유도된다.
______________________________
포흐하머 기호 혹은 하강 계승(falling factorial)은 다음처럼 정의한다.
 (1.10)
(1.10)또한 식 (1.8)이 성립하려면, 모든 $k$[= $1, 2, \cdots, n$]에 대해 다음 극한이 잘 정의되고 극한값은 $0$이 나와야 한다.
 (1.11)
(1.11)멜린 변환은 기본적으로 양방향 라플라스 변환이기 때문에, 멜린 변환이 존재하기 위한 조건은 대부분 아름답지 못하고 식 (1.11)처럼 다소 번잡하다.
[적분(integration)]
 (1.12)
(1.12)[증명]
______________________________
식 (1.11)과 비슷하게 식 (1.12)가 성립하려면, 다음 극한이 존재해서 $0$으로 가야 한다.
 (1.14)
(1.14)식 (1.12)에 있는 적분 구간을 조금 바꾸어서 식 (1.12)와 부호가 다른 멜린 변환을 얻을 수도 있다.
 (1.15)
(1.15) 2. 초등 함수의 변환(transform of elementary functions)
[단위 계단 함수(unit step function)]
 (2.1)
(2.1)[증명]
단위 계단 함수를 식 (1)에 대입해서 적분한다.
 (2.2)
(2.2)______________________________
[지수 함수(exponential function)]
 (2.3)
(2.3)여기서 $a > 0$이다.
[증명]
감마 함수에 대해 멜린 역변환을 적용하면, 다음과 같은 카엥–멜린 적분(Cahen–Mellin integral)을 얻을 수 있다.
 (2.5)
(2.5)여기서 감마 함수의 극점은 $0$과 음인 정수에 위치하므로 $\sigma > 0$이 되게 택한다.
[거듭제곱 함수(power function)]
 (2.6)
(2.6)여기서 $\Re[s + \nu] < 0$이다.
[곱셈의 역수(multiplicative inverse or reciprocal)]
 (2.7)
(2.7)[증명]
변수 $t+1$을 $(1-u)^{-1}$로 바꾸어서 베타 함수의 정의를 사용한다.
 (2.8)
(2.8)베타 함수의 특성에 의해 조건 $\Re[s] > 0$, $\Re[1-s] > 0$을 만족해야 한다. 또한 오일러의 반사 공식(Euler's reflection formula)을 이용해 식 (2.8)을 다음과 같이 더 간단히 쓸 수 있다.
 (2.9)
(2.9)______________________________
[리만 제타 함수(Riemann zeta function)]
 (2.10)
(2.10)______________________________
식 (2.11)에 의해 자연수에서만 의미 있는 제타 함수(zeta function)를 복소 영역에서 정의한 리만 제타 함수로 쉽게 확장할 수 있다.
 (2.12)
(2.12) 3. 길쌈(convolution)
[곱셈의 길쌈(multiplicative convolution) 정의] [1]
 (3.1)
(3.1)
[대수적 성질(algebraic properties)]
 (3.3)
(3.3)
[곱셈의 길쌈 정리(multiplicative convolution theorem)]
 (3.3)
(3.3)
 (3.4)
(3.4)
 (3.1)
(3.1) (3.3)
(3.3) (3.3)
(3.3)[증명]
식 (3.1)을 식 (1)에 대입해서 정리한다.
 (3.4)
(3.4)______________________________
[파르세발의 정리(Parseval's theorem)]
 (3.5)
(3.5)여기서 $\sigma$는 $F(s)$의 기본대, $1-\sigma$는 $G(s)$의 기본대에 각각 속해야 한다.
[증명]
식 (3.5)의 우변 식에서 식 (1)을 대입해서 적분을 정리한다.
 (3.6)
(3.6)______________________________
만약 $g(t)$ = $f(t)$로 두면, 파르세발의 정리는 다음처럼 바뀐다.
 (3.7)
(3.7)함수 $f(t)$가 실수인 경우는 식 (3.7)을 더 간략화할 수 있다.
 (3.8)
(3.8)[참고문헌]
[1] A. D. Poularikas (Ed.), The Transforms and Applications Handbook, 2nd ed., Boca Raton, USA: CRC Press, 2000.
[2] H. J. Eom, "Integral transforms in electromagnetic formulation," J. Electromagn. Eng. Sci., vol. 14, no. 3, pp. 273–277, Sep. 2014.
[3] C. Mystilidis, A. Vriza. A. Kargioti. P. J. Papakanellos. X. Zheng. G. A. E. Vandenbosch, and G. Fikioris, "The Mellin transform method: electromagnetics, complex analysis, and educational potential," IEEE Antennas Propag. Mag., vol. 64, no. 5, pp. 111–119, Oct. 2022.
[다음 읽을거리]
 (1.13)
(1.13)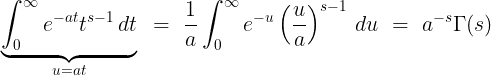
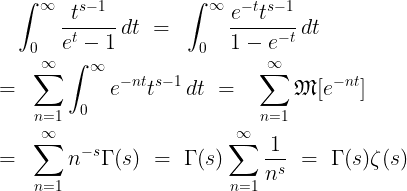 (2.11)
(2.11)

 (1)
(1)
 (1.1)
(1.1)
 (2.1)
(2.1)


 (1)
(1) (2)
(2) (3)
(3)
 (5)
(5) (6)
(6) (7)
(7)

 (10)
(10)

 (13)
(13) (14)
(14)
 (16)
(16)

 (18)
(18)