[경고] 아래 글을 읽지 않고 "자성체"를 보면 바보로 느껴질 수 있습니다.
1. 자기장
2. 자기 쌍극자 모멘트
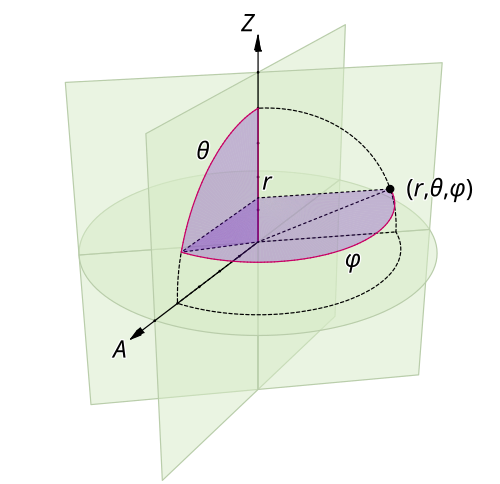
자기장(magnetic field)의 특성을 정의할 때 주변에는 아무런 물질이 없는 진공 상태를 가정하였다. 사실 이런 가정은 현실과는 매우 동떨어져 있다. 현실에 존재하는 [그림 1]과 같은 물질은 자기장 관점에서 어떻게 모형화하여야 하나?
[그림 1] 자성체의 모형화(출처: wikipedia.org)
전자기학에서는 [그림 1]처럼 모든 물질이
자화(磁化, magnetization)를 가진다고 가정한다. 이 가정은 당연하다. 물질은 양성자
(陽性子, proton)와 전자
(電子, electron)로 구성되어 있고 전자가 양성자 주위를 돌기 때문에 [그림 1]처럼 물질 내부에 매우 작은 자석이 있는 것처럼 가정할 수 있다. 물질 내부에 있는 매우 작은 자석은 미소 전류 폐로
(infinitesimal current loop)로 모형화할 수 있다. 미소 전류 고리의 특성은
자기 쌍극자 모멘트(magnetic dipole moment)로 정의한다. 하지만, 모든 물질이 자화 특성을 가진다는 가정은 양성자와 전자가 발견되기 이전에 나온 개념임을 기억하자. 잘 모르고 했지만 제대로 정의한 자화라는 개념은 당연히 실험 결과를 너무나 잘 설명했다. 거꾸로 보면 양성자와 전자의 존재성은 물질에 자기장을 걸어줌으로써 증명할 수도 있다. 이와 같이 자화를 일으키는 물질은 자성체
(磁性體, magnetic material)라 한다. 자화는 전자들 각각이 일으키기 때문에 이산적
(discrete)으로 접근해야 하지만 수학적으로 표현하기가 무척 어려우므로
연속 함수(continuous function)를 이용해 모형화한다.
[∵ 적분(연속 함수)보다 덧셈(이산 함수)이 쉽기는 하지만 무한 급수를 생각하면 적분이 더 쉽다.] 그래서, 식 (1)의 전하 밀도
(electric charge density) $\rho$ 개념을 기준으로 식 (2)의 자화 밀도
(magnetization density) $\bar M$을 정의하자. 자화 밀도는 자화도
(magnetization)로도 부른다.

(1)

(2)
여기서 $V$는 체적
(volume), $N$은 물질 구성 요소의 전체 숫자, $q$와 $Q$는 전하
(electric charge), $\bar m$은 자기 쌍극자 모멘트
(magnetic dipole moment)이다. 전하 밀도와 자화 밀도를 정의하기 위해서는 식 (1)과 (2)의 체적을 0으로 보내야 한다. 자화 밀도 정의인 식 (2)에서 조심할 부분은 식 (3)처럼
맥스웰 방정식을 대칭으로 만들기 위해 도입한 자류 밀도
(magnetic current density)와는 다름을 기억해야 한다.

(3: 패러데이의 법칙)
전자기학에서는 헷갈리게도 자화 밀도와 자류 밀도를 같은 문자인 $\bar M$으로 쓰기 때문에 읽을 때나 사용할 때 항상 조심해야 한다. 구별을 위해 자류 밀도를 $\bar M_c$
[자류(magnetic current)의 c], 자화 밀도를 $\bar M_m$
[자화(magnetization)의 m]이라 하면, 자화 밀도와 자류 밀도의 관계는 $\bar M_c$ = $\mu_0 \partial \bar M_m / \partial t$가 된다.
[∵ 식 (16)을 식 (3)에 넣고 전개하면 얻을 수 있다.]
식 (2)를 이용하면 식 (4)에 있는
하나의 자기 쌍극자 모멘트가 만드는 자기 벡터 포텐셜 $\bar A(\bar r)$을 식 (5)의 일반적인 물질에 대한 자기 벡터 포텐셜
(magnetic vector potential)로 확장할 수 있다.

(4)

(5)

(6)
다음으로 아래
벡터 항등식(vector identity)도 생각하자.

(7)

(8)

(9)
식 (7)–(9)를 식 (5)에 대입해 정리하면 자성체에 대해서도 식 (6)과 유사한 형태를 얻을 수 있다.

(10)

(11)
이와 같은 복잡한 과정을 따라온 이유는 식 (6)처럼 만들기 위해서다. 식 (6)과 (10)을 비교하면 새로운 전류 밀도(current density)를 정의할 수 있다.

(12)
여기서 $\bar J_{ms}'$는 표면 전류 밀도
(surface current density)이며 $\bar J_m'$은 체적 전류 밀도
(volume current density)이다. 그러면 자화를 일으키는 자기 쌍극자 모멘트를 마치 전류처럼 취급할 수 있다. 자화를 만드는 전류는 자화 전류
(magnetization current) 혹은 구속 전류
(bound current)라 하고 자유 전자가 흘러 생기는 전류는 자유 전류
(free current)라 한다. 이 개념을 이용해서 자성체가 있는 경우의 자속 밀도를 구해보자. 먼저
진공 중의 자속 밀도는 아래와 같이 표현된다.

(13)
자성체가 있으면 자유 전류 밀도 $\bar J_f$와 자화 전류 밀도 $\bar J_m'$이 함께 있으므로 식 (13)을 아래처럼 바꾸어야 한다.

(14)
여기서 $\bar H$는 자기장
(magnetic field)이다.
회전 연산자의 의미에 의하면 자기장의 원천은 자유 전류이다. 반면에 자속 밀도의 원천은 자유 전류 및 자화 전류와 관련된다. 만약 자유 전류는 없고 자화 전류만 있다면 $\bar H$ = $0$이 될까? 아니다. 식 (14)를 보자. 자기장의 회전이 0이지
[∵ 자유 전류가 없으므로] 자기장이 0임은 아니다. 이 점은 주의해야 한다. 또한 식 (12)에 있던 표면 전류 밀도는 식 (14)의 체적 전류 밀도에 포함되어 있다고 생각해야 한다.
[∵ 체적 전류 밀도의 특별한 경우가 표면 전류 밀도이다.] 예를 들면, 어떤 면적 $s'$
[오른손 법칙으로 정한 둘레 방향은 $c'$]에 존재하는 전체 자화 전류
($I_\text{tot}$)를 다음처럼 생각하자.

(15)
여기서 $\hat a'$ = $\hat n' \times \hat l'$, $\hat a'$는 면적 $s'$의 방향이며 $\hat n'$은 둘레를 구성하는 폐곡선 $c'$를 바깥으로 뚫고나가는 방향이다.
[$\hat n'$는 $\hat a'$에 수직이다. 원기둥의 부피를 똑바로 자른 단면이 $s'$라면, $\hat n'$ = $\hat \rho$, $\hat l'$ = $\hat \phi$, $\hat a'$ = $\hat z$가 된다.] 유전체 속의 전체 구속 전하($Q_\text{tot}$)처럼 자성체의 전체 자화 전류는 항상 0이다. 이는 물질의 자화 특성을 보여준다. 외부 자기장이 가해지지 않으면 물질은 자성이 없다.
[물론 외부 자기장이 없어도 영구 자석은 자기장이 있다.] 자기장이 가해지면 자화하지만 원래 자화 전류는 없었기 때문에, 자기장에 의해 생성된 표면과 체적 자화 전류 밀도는 식 (15)처럼 서로 상쇄한다. 식 (14)의 마지막식은 자성체까지 적용될 수 있는
맥스웰 방정식(Maxwell's equations)의 일반형이다. 식 (14)에 의하면 자화 밀도를 알 경우 자성체가 있는 문제도 쉽게 해결할 수 있다. 그런데, 자화 밀도를 정확히 알기는 쉬운 문제가 아니다.
[∵ 식 (2)에 의해 물질내에 있는 모든 자기 쌍극자 모멘트를 계산해서 벡터적으로 더해야 한다.] 그래서, 근사이기는 하지만 자화 밀도는 자기장과 선형 비례한다고 가정하자.

(16)
여기서 $\chi_m$는 자기 감수율(magnetic susceptibility)이며 $\mu_r$은 비투자율(relative permeability)이라 한다. 식 (16)의 둘째식은 자기장과 자속 밀도의 구성 관계식(constitutional relation)이라 부른다. 자성체 매질을 측정하는 관점에서 보면, 당연히 자기장과 자화 밀도의 관계는 식 (16)의 첫째식처럼 표현된다. 현재 매질의 투자율을 재려면 외부 도선에 전류를 흘려서 자기장을 만들어야 한다. 그 다음에 진공일 때와 매질이 있을 때의 자기력 혹은 자속 밀도[정확히는 인덕턴스(inductance)]를 재면 자화 밀도를 측정할 수 있기 때문에, 식 (16)처럼 정의함이 타당하다. 다만 강자성(强磁性, ferromagnetism)은 선형으로 표현되지 않고 복잡한 비선형 특성을 가지므로 식 (16)은 잘 맞지 않지만, 자기장을 이용해 자화 밀도를 표현한다는 기본 개념은 강자성에도 여전히 통한다. 자성체 내부에 생기는 자속 밀도도 식 (16)으로 계산할 수 있다. 왜냐하면 식 (10)의 자성체에 대한 자기 벡터 포텐셜 관계식은 자기 쌍극자 모멘트 근처[$R \approx 0$]에서는 맞지 않지만 주변에 워낙 많은 원자가 있기 때문에 $R$ = $0$에 있는 하나의 자기 쌍극자 모멘트에 의한 기여는 무시할 수 있다고 가정한다.[혹은 식 (10)에서 체적을 0으로 가져가면 체적 적분도 0으로 간다.]
우리가 사용하는 MKS(meter–kilogram–second) 단위에 쓰는 자기장 $\bar H$의 표준 단위는 A/m, 자속 밀도 $\bar B$의 표준 단위는 T[테슬라, tesla]이다. 예전에 쓰던 혹은 CGS(centimeter–gram–second) 단위로 표현한 자기장의 단위는 Oe[외르스테드, oersted], 자속 밀도의 예전 단위는 G 혹은 Gs[가우스, gauss]이다. 자기장에 대한 MKS와 CGS 단위는 다음처럼 변환할 수 있다.
 (17)
(17)
원래 CGS 단위로 정의했던 자기장과 자속 밀도의 구성 관계식은 $\mu_0$없이 비투자율 $\mu_r$만 있어서 매우 간단했다.
 (18)
(18)
여기서 자성체가 없는 진공 조건에서는 1 Oe = 1 G로 간주한다. 식 (18)을 약간 변형해서 MKS 단위로 표현한 자기장과 자속 밀도의 구성 관계인 식 (16)도 유도할 수 있다.
 (19)
(19)
자화 밀도 $\bar M$를 이용해서 식 (18)을 변형하기도 한다.
 (20a)
(20a)

(20b)
여기서 상수 $4 \pi$는 $\mu_0$의 흔적이다. 식 (17)에 있는 1 G가 만분의 1 T인 이유는 지구 자기장(earth's magnetic field or geomagnetic field)과 관계 있다. 지구 자기장은 지역마다 차이가 나지만 대략 1 G 정도[정확히는 0.25~0.65 G]이다. 1 G는 상당히 센 자속 밀도이다. 왜냐하면 1 A가 공급된 전기 장판(electric blanket)에서 나오는 60 Hz 자속 밀도의 평균값은 대략 20 mG[RMS 기준 14 mG] 정도이며[3],[1 A가 흐르는 무한 도선에서 10 cm 떨어진 위치의 자속 밀도는 $(\mu_0 \cdot 1)\mathbin{/} (2 \pi \cdot 0.1)$로 계산되어 약 20 mG이다.] 이 조건에서 전류를 다시 50 A로 높여야 1 G를 얻을 수 있기 때문이다.
그런데 수학자인 가우스Carl Friedrich Gauss(1777–1855) 이름이 왜 지구 자기장과 관계된 단위인 G에 쓰일까? 가우스는 수학자이기도 하지만 천문학자 겸 물리학자이다.[예전에는 수학만으로 밥벌이하기가 무척 어려웠다.] 가우스는 동료 교수인 베버Wilhelm Eduard Weber(1804–1891)와 함께 1831년가우스 54세, 조선 순조 시절부터 유럽을 돌아다니면서 지구 자기장을 측정하고 연구했다[2]. 가우스와 베버는 지구 자기장에 대해 놀라운 통찰력이 있었다. 바로 지구 자기장은 N극과 S극, 딱 두 곳만 있다는 믿음이다. 지구 자기장에 대한 놀라운 통찰[Gauss' new theory of geomagnetism]을 실험적으로 검증하면서 드디어 1839년에 새로운 지자기 이론을 완성했다. 이후 1840년에 가우스의 지자기 이론이 출판되어서 학계에 널리 알려졌다. 이 중에서 가장 중요한 과학적 결과는 지금도 쓰이고 있는 지자기를 이용한 위치 측량이다[2]. 또한 CGS 단위는 1832년가우스 55세, 조선 순조 시절에 가우스가 제안한 길이, 질량, 시간에 대한 절대 단위에 기반을 두고 있어서 가우스 단위(Gaussian units)라고도 한다.
전기력 $\bar F_e$와 자기력 $\bar F_m$을 정량화한 쿨롱Charles-Augustin de Coulomb(1736–1806)은 실험할 때에 정전기와 자석을 힘의 원천으로 사용했다. 정전기로 전하를 모아서 두 전하에 작용하는 힘을 전기력으로 정했고, 전류가 자석을 만든다는 사실을 몰라서 자기력 측정에는 자석을 이용했다. 이후 정전기가 생성하는 전기장 $\bar E$와 자석의 속성인 자속 밀도 $\bar B$를 전기력과 자기력을 전달하는 근원으로 선정해서 다시 공식화했다.
 (21)
(21)
다만 $\bar F_e$ 정의에는 $\bar E$를 사용하고, $\bar F_m$에는 자기장 $\bar H$ 대신 $\bar B$를 쓰는 선택은 균형이 맞지 않아 어색함이 있다. 전자파의
복사 전력(radiated power) 정의
[$\bar S$ = $\bar E \times \bar H$]라든지 파동 방정식에는 $\bar B$ 대신 $\bar H$가 나오는 상황도 무척 불편하다. 하지만 $\bar E$는 일관되게 쓰고 $\bar B$와 $\bar H$는 선별적으로 택하는 방식은 필연적이다. 이를 이해하려면
유전체(dielectric)와 자성체의 특성을 살펴봐야 한다. 충전된
커패시터(capacitor)에 유전체를 채우면,
분극(polarization)으로 인해 내부 전기장이 줄어들지만 커패시터에 저장된 전하량 자체는 그대로이다. 다른 유전체로 아무리 바꾸어도 이 현상은 변함이 없다.
[이를 유전체에 대한 패러데이 실험(Faraday experiment on dielectric)이라 부른다.] 그래서 변하지 않는 전기 묶음인
전속(electric flux)을 정의할 때는 전기장이 아닌
전속 밀도(electric flux density) $\bar D$를 새롭게 도입해서 사용한다. 다른 관점으로 전기력에 쓰이는 전기장은 물질 속에서 보존되지 않고 변해서 물질의 특성을 반영한 전기력의 구성 요소가 된다. 하지만 자기력은 전기력과 다르게 움직인다. 자기력 실험에 쓰이는 자석은 전류로 만들 수 있고 자성체의 자화
(magnetization)까지 포함한다. 왜냐하면 전류가 자석을 만들 때는 N극만 혹은 S극만 따로 생성할 수 없고 항상 N극과 S극이 같은 양으로 생기고, 자화를 만드는
미소 전류 폐로(infinitesimal current loop)도 N극과 S극을 같이 만들기 때문이다. 그래서 자기력을 만드는 장은 자기 묶음인 자속
(magnetic flux)과 관련되며, 특정 면적에 들어온 자속 밀도는 그 면적을 그대로 빠져나가는 보존성을 가진다. 결국 자속 밀도는 보존되지만 미소 전류 폐로의 기여분을 모두 가지고 있으므로, 자속 밀도가 자성체의 물질적 특성을 표현한다. 이런 이유로 전기나 자기 묶음의 보존성은 발산 연산자와 연결된다. 그래서 발산 연산자의 특성에 따라 전속이 바뀌지 않는 성질은 $\bar \nabla \cdot \bar D$ = $\rho$가 되고, 자속의 연속성은 $\bar \nabla \cdot \bar B$ = $0$으로 표현된다. 전자파에서 $\bar B$ 대신 $\bar H$를 쓰는 이유는
맥스웰이 수정한 암페어의 법칙 때문이다. 커패시터 내부를 흐르는 변위 전류 밀도 $\partial \bar D / \partial t$를 시간적으로 바꾸면, 자속 밀도 $\bar B$가 아닌 자기장 $\bar H$의 회전이 생긴다. 왜냐하면 도선을 흐르는 전류가 변위 전류와 연속을 이루고 전류는 자기장의 회전을 생성하기 때문이다. 반면에 전기력을 만든 전기장의 회전은 패러데이의 법칙에 따라 자속 밀도의 시간 변화 $\partial \bar B / \partial t$와 직접 연결된다. 따라서 $\bar E$와 $\bar H$의
회전[$\bar \nabla$]으로 생성되는 전자파 특성은 당연히 전기장과 자기장으로 설명한다.
[참고문헌]
 (1)
(1) (2)
(2)
 (1)
(1) (2)
(2) (3: 패러데이의 법칙)
(3: 패러데이의 법칙) (4)
(4) (5)
(5) (6)
(6) (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16)



 (20b)
(20b)


 (1)
(1) (2)
(2)

 (3)
(3) (4)
(4) (6)
(6) (7)
(7) (8)
(8) (9)
(9)
 (10)
(10) (11)
(11)


