1. 자기장
2. 전기 쌍극자 모멘트

[그림 1] 자기 쌍극자
유전체(誘電體, dielectric)의 성질을 설명하기 위해 분극(分極, polarization) 개념을 이용하는 것처럼 자성체(磁性體, magnetic material)를 정의하기 위해 자화(磁化, magnetization)를 이용한다. 즉, 자성체는 자화를 만들 수 있는 물질이라고 정의한다.

[그림 2] 자기 쌍극자가 만드는 자기장(출처: wikipedia.org)
자기장(magnetic field)은 전기장(electric field)과는 다르게 자하(磁荷, magnetic charge)가 없기 때문에 독특한 성질을 가진다. 따라서, 자성체는 유전체와 다르게 정의한다. [그림 1]처럼 자기 쌍극자(magnetic dipole)를 정의하기 위해 N극과 S극을 가진 자하를 가정하지 않고 미소 전류 폐로(infinitesimal current loop)가 [그림 2]와 같은 자기 쌍극자 자기장을 만든다고 생각한다. 즉, 자성체가 자기를 띠는 이유는 물질 내부에 [그림 1]과 같은 미소 전류 고리가 많기 때문이다. [그림 1]과 같이 자기 쌍극자를 정의하는 개념은 상상이었지만 물질 내부의 특성을 매우 잘 설명한다. [그림 1]과 같은 개념을 발명한 사람은 우리가 잘 아는 암페어André-Marie Ampère(1775–1836)이다. 암페어는 미소 전류 고리를 이용해 자성체의 특성을 명쾌하게 설명했다. 전자(電子, electron)와 양성자(陽性子, proton)가 발견되기 훨씬 이전에 이런 멋진 설명한 암페어는 틀림없이 뛰어난 천재이다. 그러면 식 (1)의 자기 벡터 포텐셜(magnetic vector potential) 정의를 이용해 [그림 1]의 미소 전류 고리가 만드는 자기장을 계산해본다.
 (1)
(1)
관측점(observation point) $r$이 미소 전류 고리가 있는 $(x', y', 0)$보다 멀리 떨어져 있다고 가정하면 자기 벡터 포텐셜을 아래로 근사화할 수 있다.
 (2)
(2)
여기서 $r = \sqrt{x^2 + y^2 + z^2}$이며, $\sqrt{1+x}$, $1/(1+x)$ 형태 함수를 근사화하기 위해 테일러 급수(Taylor series) 전개를 이용하여 $1/R$을 간략히 하였다. 또한, 식 (2)의 계산에는 [그림 3]과 같은 구 좌표계(spherical coordinate system)를 사용하였다. 즉, $x = r \cos \phi$, $y = r \sin \phi$, $x' = a \cos \phi'$, $y' = a \sin \phi'$를 근사화된 $1/R$ 식에 대입하면, 식 (2)의 마지막식이 얻어진다.[$\oint_0^{2 \pi} 1/r ~d \phi' \hat \phi' =0$임을 기억한다.]
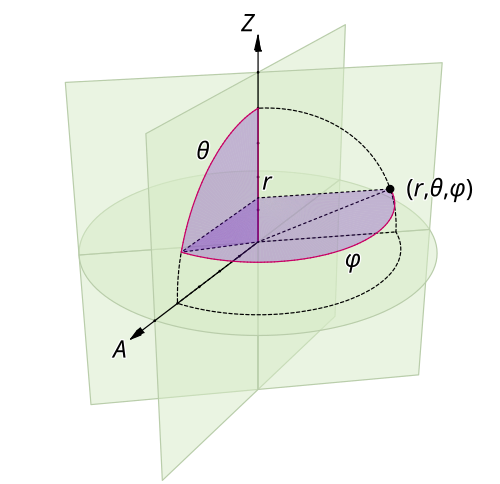

[그림 3] 구 좌표계의 표현(출처: wikipedia.org)
식 (2)를 선 적분하기 위해서는 식 (3)처럼 단위 벡터(unit vector) $\hat \phi$를 데카르트 좌표계(Cartesian coordinate system)의 단위 벡터 $\hat x$, $\hat y$로 바꾸어야 한다.[∵ 단위 벡터 $\hat \phi$는 위치에 따라 계속 방향이 변하기 때문에 적분에 대해 상수가 아니다.]
 (3)
(3)
식 (3)을 식 (2)에 대입해 적분하면 아래와 같다.
 (4)
(4)
식 (4)에 등장하는 전류와 면적의 곱 $I \pi a^2$은 자기 쌍극자 모멘트 혹은 자기 쌍극자 능률(magnetic dipole moment)로 정의한다. 모멘트 혹은 능률(能率, moment)은 어떤 물리량이 변하는 특정 경향이다. 조금 더 세밀하게 봐서 모멘트는 곱 연산으로 나타낸 핵심 측정량(measure)을 뜻한다. 식 (4)에서 원천을 변화시키는 중요한 요소는 당연히 $I \pi a^2$이므로, 독립적인 두 항인 전류와 면적을 선택해서 모멘트를 도출한다.
 (5)
(5)
자기 쌍극자 모멘트가 들어있는 식 (5)는 전기 쌍극자 모멘트(electric dipole moment)가 들어있는 식 (6)과 매우 유사하다.
 (6)
(6)
다음으로 식 (1)을 이용해 자속 밀도(magnetic flux density)를 계산한다.
 (7)
(7)
식 (5)를 식 (7)에 대입하면 자기 쌍극자가 만드는 자속 밀도를 얻을 수 있다.
 (8)
(8)
식 (8)은 전기 쌍극자가 만드는 전기장과 동일한 형태를 가진다.
 (9)
(9)
식 (8)과 (9)의 결과는 놀랍도록 서로 닮아있다. 전기 쌍극자와 자기 쌍극자에서 출발한 식이 서로 같으므로, [그림 1]의 미소 전류 고리가 자기 쌍극자 역할을 한다는 사실을 분명히 알 수 있다.
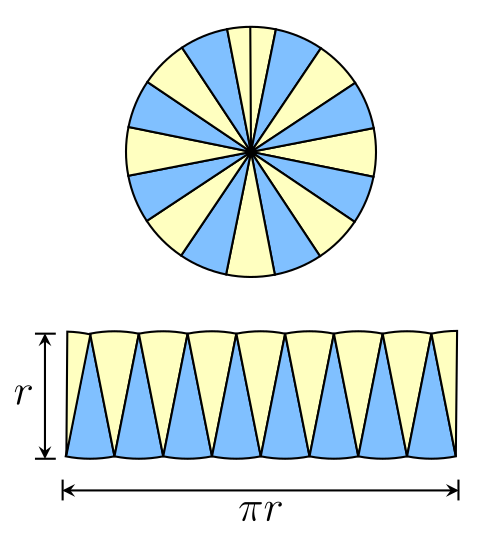
[그림 4] 원의 면적 정의(출처: wikipedia.org)
식 (5)의 자기 쌍극자 모멘트는 [그림 1]처럼 원(circle)에 대해서만 정의되어 있으므로, 이를 확장할 필요가 있다. [그림 4]처럼 원의 면적 정의[삼각형을 무수히 모으면 원의 면적이 됨]를 이용해 자기 쌍극자 모멘트 $\bar m$을 일반화한다.
 (10)
(10)
식 (10)에 있는 1/2는 삼각형 면적 때문에 도입되었다. 식 (10)에 있는 벡터 $\bar r$과 $d \bar r$은 같은 평면에 있다고 가정하고 원의 면적 정의를 적용하였다. 벡터 $\bar r$과 $d \bar r$이 다른 평면에 있으면 자기 쌍극자 모멘트를 어떻게 정의해야 하는가? 벡터의 원점을 바꾸기 위해 새로운 원점을 벡터 $\bar r_0$라고 한다. 그러면 식 (10)은 아래처럼 바뀐다.
 (11)
(11)
여기서 벡터 $\bar r_0$는 상수이며 벡터의 차이 $\bar r - \bar r_0$는 $\bar r_0$에서 $\bar r$로 향하는 벡터이다. 식 (11)은 어떤 위치 벡터(position vector) $\bar r$에 대해서도 식 (10)이 자기 쌍극자 모멘트의 정의임을 의미한다.

[그림 5] 미소 네모 고리에 생기는 자기력
자기 쌍극자 모멘트 $\bar m$이 만드는 회전력(torque) $\bar \tau$를 유도한다. 먼저 임의의 모양을 가진 고리는 [그림 5]와 같은 미소 네모 고리의 합으로 표현할 수 있음을 기억한다. 그러면 [그림 5]의 조건에서 행한 증명은 임의의 고리 구조로 쉽게 확장될 수 있다. 먼저 [그림 5]에 작용하는 자기력을 이용해서 회전력을 정의한다.
 (12)
(12)여기서 매우 작은 면적을 가진 미소 네모 고리에서 $\bar B$는 거의 일정하다고 가정한다.[∵ 영역을 계속 좁혀갈 때도 $\bar B$가 지속적으로 바뀐다면, $\bar B$의 미분이 한없이 커진다는 뜻이라서 실제 현상과는 멀어지게 된다.] [그림 5]에 대해 식 (12)의 최종식을 계산한다.
 (13)
(13)따라서 자기력에 의한 회전력은 다음과 같이 간단하게 공식화된다.
 (14)
(14)[다음 읽을거리]
1. 자성체의 비밀
자기쌍극자가 자기장속에서 만드는 전기장도 있나요? 있다면 어떻게 생겼을까요?
답글삭제정자장의 경우, 자기 쌍극자는 자기장만 만듭니다. 전기장은 만들 수 없습니다.
삭제교류가 되면, 당연히 전자파가 되기 때문에 전기장과 자기장이 함께 나오고요.
1/R 을 근사화 하는 과정을 좀더 자세하게 적어주실순없나요 ? ㅠㅠ
답글삭제신재현님, 본문을 약간 수정했습니다. 계속 헷갈리면 아래 테일러 급수 부분을 다시 보세요. ^^
삭제http://ghebook.blogspot.kr/2010/07/taylor-series.html
전파거북이님. 식 (2)에서 xx'/r^2-yy'/r^2에서 2*가 빠진 것 같아요 :)
답글삭제음.. 1/R 을 x'^+y'^2+z'^2을 탈락시키고 근사하면 r(1-2*xx'/r^2-2*yy'/r^2)^1/2이 되는데, 여기서 더 근사를 하는 방법이 있나요?
삭제식은 맞습니다, 이재님. 다 전개한 후에 테일러 급수 이용해 추가로 근사화합니다.
삭제아 두번 테일러 전개를 한 거네요. 감사합니다 ㅎㅎ
삭제자기 쌍극자에 대해 이해는 했는 데 결국 이걸 뭘로 정의해야할까요? 자기장에 반응하여 토크를 변화시키는 경향 정도로 정의시켜야하나요? 뭔가 정의를 보면 딱 느낌이 오는 식으로 정리하고 싶은데 좀 애매해서 그런데 혹시 알려주실 수 있나요?
답글삭제자기 쌍극자가 모여서 자성체가 됩니다. 즉 자성체의 물성을 설명하는 기본 단위가 자기 쌍극자여서 매우 중요한 개념입니다.
삭제전파 거북이님 죄송한데 3(m*r)r-m 이부분 유도하는 것을 A에서 수학적으로 curl 해서 푸는 방법은 없나요?
답글삭제Unknown님, 제가 질문 의도를 잘 이해했는지 모르겠네요. ^^
삭제식 (8)은 식 (5)에 회전 연산을 취해 얻은 거예요. 근사하지 않고 전류부터 시작해 식 (8)을 얻으려면 식 (1)에 등장하는 적분이 문제에요.
(2)식에서 1/r 적분값이 0이 되는 이유가 r이 2파이보다 커서 0에 근사한다는 건가요?
답글삭제맞습니다. 관측점이 원천에서 매우 멀다고 가정했어요.
삭제(12)식 다음에 “여기서 B는 미소 네모 고리에서 동일하다고 가정한다”
답글삭제발산이나 회전을 계산할 때(예를 들어 전속밀도의 거리에 따른 변화율을 더하거나 뺌)와 달리 자속밀도가 동일하다고 가정할 수 있는 이유가 궁금합니다
미소 고리가 매우 작기 때문에, 자속 밀도는 거의 일정하다고 가정합니다.
삭제답변 감사드립니다!
답글삭제미소폐곡로(네모고리 회로)에 암페어 주회법칙을 이용하여 벡터회전식을 유도할 때 미소폐곡로의 각 변의 자계는 중심점의 자계에 거리에 따른 자계의 변화율을 가감하여 계산합니다. 이 경우에도 미소 고리는 매우 작다고 가정하는데 자계를 동일하다고 가정을 안합니다 그 차이가 궁금합니다.
간단하게 테일러 급수를 생각해보세요. 예를 들어, $f(x+\Delta x) \approx f(x) + f'(x) \Delta x$라 합시다. 그냥 $f(x)$만 생각하면 거의 $f(x+\Delta x) \approx f(x)$가 됩니다. 하지만 함수의 차이 $f(x+\Delta x) - f(x)$는 분명히 $f'(x) \Delta x$만큼 존재해요. 이 값을 $\Delta x$로 나누면 무시할 수 없는 값(당연 미분)이 됩니다.
삭제이 두 경우를 한 번 비교하면 이해가 될 겁니다.
안녕하세요, 전자기학을 공부하는 학생입니다. 언제나 큰 도움을 받고 있습니다.
답글삭제식 (10)에서 자기 쌍극자 모멘트를 일반화하는 개념이 잘 이해가 되지 않아서 질문 드립니다.
맨 처음에 미소 원형 고리를 가정하고 자기 벡터 퍼텐셜을 구한건데 그림 4에서 원을 사각형 형태로 펼치게 되면 미소 전류가 흐르는 위치가 변하게 되어 A의 값이 달라져야 할 것 같은데 고리의 모양을 임의로 변형해도 왜 같은 결과가 나오는지 궁금합니다!
미소 전류 고리에 대한 논증에 의해 자기 쌍극자 모멘트는 미소 고리의 면적에 비례합니다.
삭제이를 바탕으로 [그림 4]처럼 작은 면적을 원하는 모양대로 모으면, 어떤 면적이든 생성할 수 있기 때문입니다.
답변 감사드립니다! 스트로크의 정리 증명에서 미소 사각형 면적을 무한히 적분해서 임의의 면적을 형성했는데, 같은 일을 미소 원형 모양의 면적으로도 할 수 있다는 거죠?
삭제네, 비슷합니다.
삭제