[경고] 아래 글을 읽지 않고 "아벨의 적분 방정식"을 보면 바보로 느껴질 수 있습니다.
대부분의
적분 방정식(integral equation)은 정확한 해법이 존재하지 않기 때문에 피적분 함수를 적절한 기저 함수
(basis function)로 분해해서 수치 해석적으로 적분 방정식의 해를 근사화한다. 예외적으로 적분 방정식이 깔끔하게 풀리는 경우도 어쩌다 한 번 정도는 있다. 그 대표적인 예가 다음과 같은
아벨의 적분 방정식(Abel's integral equation)[1]이다.

(1)
여기서 $f(0)$ = $0$, $0 < \alpha < 1$이다. 아벨의 적분 방정식은 $t$ = $x$에서 피적분 함수가 발산하는 매우 특이한 성질을 가진 특이 적분 방정식
(singular integral equation)이다. 식 (1)의 풀이법은 아벨
Niels Henrik Abel(1802–1829)이 1823년
아벨 21세, 조선 순조 시절에 제안했다.
베타 함수(beta function)를 적용하면 식 (1)을 쉽게 증명할 수 있다. 먼저 식 (1)의 왼쪽 식을 $(x-t)^{1- \alpha}$로 나눈 후 $t$에 대해 적분한다.

(2)
 (3)
(3)
따라서 식 (3)을 식 (2)에 대입한 후 $x$에 대해 미분하면 식 (1)이 증명된다.

(4)
식 (1)의 오른쪽 식에 나타난 적분에 미분 연산 $d/dx$를 적용하기 위해
부분 적분(integration by parts)을 기반으로 피적분 함수의 특이성을 제거한다.

(5)
여기서 $f'(t)$ = $df(t)/dt$이다. 식 (5) 우변의 첫째 항을 $x$에 대해 미분하면 다음 결과를 얻는다.
 (6)
(6)
다음 단계로 둘째 항도 미분을 해야 하지만, 피적분 함수와 적분 구간에 $x$가 모두 있어서 미분이 어렵다. 이런 어려움을 피하기 위해 $(x-a)^\alpha$를
뉴턴의 이항 정리(Newton's binomial theorem)로 전개해서 적분하고 미분한다.

(7)

(8)
여기서 $(\alpha)_k$는
포흐하머 기호(Pochhammer symbol) 혹은 하강 계승
(falling factorial)이다. 식 (8)을 더 쉽게 유도하려면
정적분의 미분 관계를 이용해야 한다. 식 (6)과 (8)을 합쳐서 $\phi(x)$를 더 간단하게 표현한다.

(9)
식 (1)의 적분 구간을 다음처럼 $0$에서 무한대로 바꾸어서 조금 다른 공식을 만들 수도 있다.

(10)
여기서 $\lim_{x \to \infty} f(x)$ = $0$이다. 식 (10)의 유도는 식 (2)와 비슷한 과정을 거친다.
 (11)
(11)
식 (5)처럼 피적분 함수의 특이성을 없애기 위해 식 (10)의 오른쪽 식을 부분 적분한다.

(12)
다음 단계로 식 (12)의 우변을 $x$에 대해 미분하여 정리한다.

(13)

(14)
식 (13)과 (14)를 합친 후, 식 (10)의 오른쪽 식에 대입해서 최종 결과를 얻는다.

(15)
아벨의 적분 방정식에 나오는 $\phi(x)$는 어떤 함수든지 가능하므로, 식 (1)의 적분 방정식을 적분 변환(integral transform) 형태로 정의하기도 한다. 즉 아벨 변환(Abel transform)과 아벨 역변환(inverse Abel transform)이란 이름을 붙여서 식 (1)을 다음처럼 표기할 수 있다.

(16)
여기서 $df(\chi)$ = $f'(\chi) d\chi$이다. 식 (16)의 마지막식처럼 표현한 적분은
리만–스틸체스 적분(Riemann–Stieltjes integral)이라 부른다.
아벨의 적분 방정식은
분수 미적분학(fractional calculus)으로 개념화하기도 한다. 아벨 사후 3년 뒤인 1832년
리우빌 23세, 조선 순조 시절에 리우빌
Joseph Liouville(1809–1882)이 분수 미분과 적분
(fractional differentiation and integration)을 제안했고, 1847년
리만 21세, 조선 헌종 시절에는 리만
Bernhard Riemann(1826–1866)이 분수 미적분학을 복소 영역
(complex domain)으로 확장했다. 한참 시간이 흐른 1893년
헤비사이드 43세, 조선 고종 시절에 헤비사이드
Oliver Heaviside(1850–1925)가
연산 미적분학(operational calculus)을 새롭게 제안하면서 분수 미적분학을 다시 강조했다. 그래서 식 (1)에 나오는 적분을 다음과 같은
리만–리우빌 적분(Riemann–Liouville integral)이라고 부른다.

(17)
식 (17)의 정의를 이용해서 식 (1)의 왼쪽 식을 다시 쓴다.

(18)
순전히 연산자 관점으로만 식 (18)의 좌변을 본다. 그러면 분수 적분인 식 (18)을 다시 분수 미분해주면 원래 함수 $\phi(x)$가 당연히 나온다.
 (19)
(19)
따라서 분수 미적분학을 이용해도 식 (1)과 같은 관계가 유도된다.
1. 기본(basics)
아벨의 적분 방정식은 아래처럼 다양한 방식으로 표현될 수 있다.
[기본 표현식]

(1.1)

(1.2)
여기서 $f(0)$ = $0$,
$0 < \alpha < 1$이다.
[증명]
식 (1.1)에 있는 변수를 $u = t^2$과 $v = x^2$로 치환해서 식 (1)과 비교하여 증명한다. 비슷하게 식 (1.2)는 변수 치환을 통해 식 (10)으로 만든다.
______________________________
라돈 변환(Radon transform)처럼 원통 좌표계에 등장하는 적분 방정식의 해를 구할 때에는 식 (1.1), (1.2)가 매우 편리하다.
[참고문헌]
[다음 읽을거리]


 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
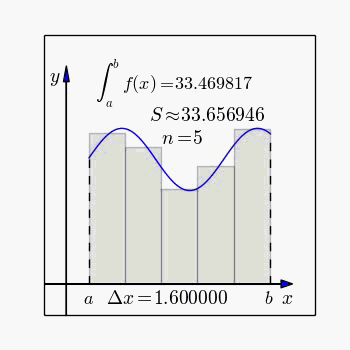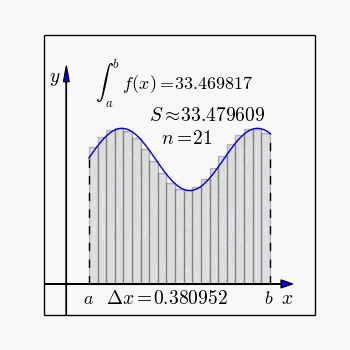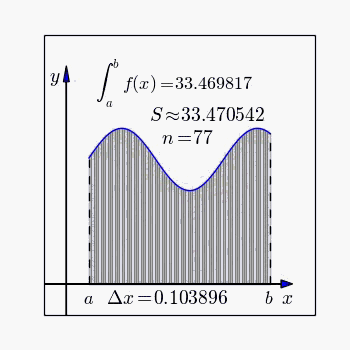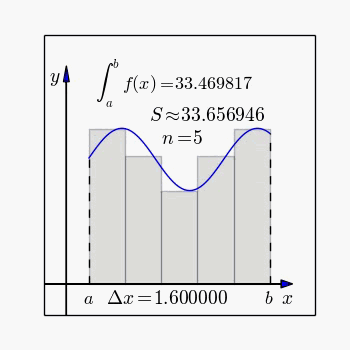
(6)
 (1)
(1) (2)
(2) (3)
(3) (4)
(4)

 (7)
(7) (1)
(1) (2)
(2)
 (4)
(4) (5)
(5)
 (7)
(7) (8)
(8) (9)
(9) (10)
(10)
 (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16) (17)
(17) (18)
(18)
 (1.1)
(1.1) (1.2)
(1.2)