[경고] 아래 글을 읽지 않고 "푸리에 변환의 성질"을 보면 바보로 느껴질 수 있습니다.
[그림 1] 푸리에 변환의 시간 이동 예(출처: wikipedia.org)
1. 기본(basics)
[정의]
(1.1)[선형 사상(linear mapping or linearity)]
(1.2)여기서 $G(\omega)$는 $g(t)$의 푸리에 변환이다.
[시간 및 주파수 편이(time and frequency shifting)]
(1.3)여기서 $t_0$은 시간 지연(time delay), $\omega_0$은 변조(modulation) 각주파수이다.
[쌍대성(duality)]
(1.4)
(1.5)[켤레 복소수(complex conjugate)와 대칭성(symmetry)]
(1.6a: $f(t)$는 복소 함수)
(1.6b: $f(t)$는 복소 함수)
(1.6c: $f(t)$는 복소 함수)
(1.7: $f(t)$는 실수 함수)여기서 $(\cdot)^*$는 켤레 복소수, 식 (1.6)과 (1.7)은 각각 $f(t)$가 복소 및 실수 함수인 경우이다.
[미분(differentiation)]
(1.8)
(1.9)여기서 $\lim_{t \to \pm \infty} f(t)$ = $0$이라 가정한다. 식 (1.9)를 연속적으로 적용하면, 식 (1.8)의 둘째식이 증명된다.
______________________________
(1.10)
(1.11)
(1.12)
(1.13)
(1.14)
식 (1.8)은 페이저(phasor) 개념과 매우 유사하다. 우리 예상처럼 페이저 이론은 푸리에 변환의 특별한 경우이다. 더 나아가면 헤비사이드Oliver Heaviside(1850–1925)가 제안한 연산 미적분학(operational calculus)까지 우리 사고를 확장할 수 있다.
[적분(integration)]
(1.10)[증명]
적분된 함수를 식 (3.1)에 있는 길쌈(convolution) 형태로 바꾸어서 식 (3.3)의 첫째식처럼 푸리에 변환하면 증명된다.
(1.11)추가적으로 식 (1.10)의 증명에 식 (2.7)이 꼭 필요하다.
______________________________
적분은 미분의 역연산이므로, 식 (1.10)에서는 $i \omega$ 항이 분모로 간다. 다만 DC(직류, direct current) 성분[$\omega$ = $0$]에 디랙 델타 함수(Dirac delta function)가 매우 크게 출현한다.
[디랙 델타 함수(Dirac delta function)]
(1.12) (1.13)식 (1.12)과 (1.13)은 복소 함수론(complex analysis)과 푸리에 변환을 이용해 엄밀하게 증명할 수 있다.
[우함수와 기함수(even and odd functions)]
실수인 우함수와 기함수의 푸리에 변환은 각각 실수와 순허수가 된다.
[증명]
적분 구간을 나누어서 우함수 $f(t)$의 푸리에 변환을 계산한다.
(1.14)비슷한 방식으로 기함수인 $g(t)$의 푸리에 변환도 유도해서 변환값이 순허수임을 증명한다.
(1.15)______________________________
실수 영역에서는 우함수와 기함수의 특성이 비슷하지만, 복소 영역인 푸리에 변환값은 실수와 순허수가 되므로 두 함수는 확연히 다른 결과를 보인다.
[특수한 변환값]
(1.16)
(1.17)[주기 함수(periodic function)]
(1.18)여기서 $f(t+T)$ = $f(t)$, $T$는 주기, $\omega_0$ = $2 \pi \mathbin{/} T$이다.
[증명]
주기 함수라서 푸리에 급수로 전개한 후, 식 (1.16)과 식 (1.3)을 조합하여 최종 결과를 유도한다.
______________________________
2. 초등 함수의 변환(transform of elementary functions)
[그림 2.1] 구형 함수(출처: wikipedia.org)
[구형 함수 혹은 사각 함수]
(2.1a)
(2.1b)[그림 2.1]에 있는 구형 함수(矩形函數, rectangular function) 혹은 사각 함수의 정의는 다음과 같다.
(2.2).svg/500px-Sinc_function_(both).svg.png)
[그림 2.2] 표본화 함수(출처: wikipedia.org)
식 (2.1)에 등장한 $\operatorname{Sa}(\cdot)$는 [그림 2.2]에 제시한 표본화 함수(sampling function)이다.
(2.3)이 함수는 사각 함수를 이용해 신호를 표본화(sampling)할 때 생기는 주파수 영역의 특성을 표현한다. 표본화 함수는 다음과 같은 싱크 함수 $\operatorname{sinc}(\cdot)$로 표시할 수도 있다.
(2.4)표본화 함수와 싱크 함수는 서로 혼용해서 쓰이기 때문에, (2.4)를 기준으로 표본화 함수는 비정규화 싱크 함수(unnormalized sinc function), 싱크 함수는 더 구체적으로 정규화 싱크 함수(normalized sinc function)라 부르기도 한다. 싱크 함수는 사인 함수에 c를 붙여서 표기한다. 하지만 싱크 함수를 처음 사용한 저자는 설명 없이 그냥 c만 붙여서 썼기 때문에 c의 정확한 의미를 모른다[1]. 다만 싱크 함수는 $x$ = $0$을 제외한 모든 정수에서 함수값이 $0$이어서 기수(基數, cardinal number: 세는 수인 계산수)를 선택하는 기수 함수(cardinal function)로 간주할 수 있다. 조금 억지이기는 하지만 적당한 설명을 만들고 싶어서, c를 기수의 약어라고 가정한다.
식 (1.4)에 제시한 쌍대성을 이용해서 표본화 함수의 푸리에 변환도 얻을 수 있다.
(2.5)신호 처리에서 이상적인 필터(ideal filter)가 불가능함을 증명할 때, 식 (2.5)를 유용하게 사용한다. 이상적인 필터는 식 (2.5)의 우변처럼 특정 주파수 대역을 정확히 선택한다. 하지만 주파수 영역에서 이상적인 선택을 하려면, 우주 창조부터 멸망까지 필터의 시간 응답이 만들어져야 한다. 어떤 신호든 시간 영역에서 영원히 존재할 수는 없으므로, 주파수 영역에서 이상적인 필터를 구현할 수 없다.
[그림 2.3] 삼각형 함수(출처: wikipedia.org)
[삼각형 함수]
(2.6)[그림 2.3]에 보인 삼각형 함수(triangular function)는 $\operatorname{tri}(t)$ = $\Lambda(t)$ = $\max(1-|t|, 0)$으로 정의한다.
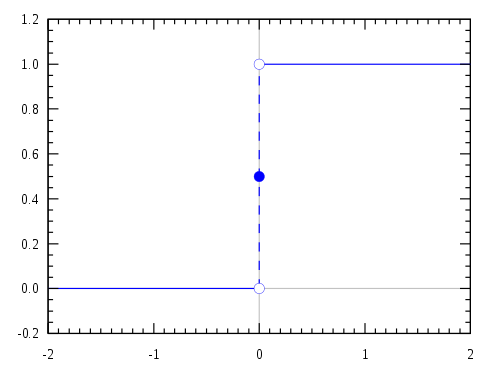
[그림 2.4] 단위 계단 함수(출처: wikipedia.org)
[단위 계단 함수]
(2.7)식 (2.7)은 극한(limit)이나 복소 함수론(complex analysis)을 이용해서 엄밀하게 증명해야 한다. 단위 계단 함수는 제안자인 헤비사이드Oliver Heaviside(1850–1925) 이름을 붙여서 헤비사이드 계단 함수(Heaviside step function)라고도 한다. 단위 계단 함수(unit step function)는 정의가 매우 간단하지만, 푸리에 변환을 구하기는 상당히 어렵다. 또한 단위 계단 함수는 푸리에 변환과 라플라스 변환(Laplace transform)을 연결하는 중요한 함수이다.
[그림 2.5] 부호 함수(출처: wikipedia.org)
[부호 함수]
(2.8)여기서 $\operatorname{sgn}(t)$는 $t$의 부호를 택하는 부호 함수(sign function)이며 $\operatorname{sgn}(t)$ = $2u(t)-1$로 표현된다.
[증명]
부호 함수 정의에 식 (2.7)과 (1.12)를 대입하여 정리한다.
(2.9)______________________________
부호 함수의 푸리에 변환 결과에서 적분 구간은 반무한으로 바꾸면 다음 적분을 정의할 수 있다.
(2.10)
(2.11)동어반복이기는 하지만, 식 (2.10)과 (2.11)을 합치면 식 (2.7)을 다시 얻을 수 있다.
[그림 2.6] 양뱡향으로 감쇠하는 지수 함수
[양방향 감쇠 지수 함수]
(2.12)로렌츠–코쉬 함수(Lorentz–Cauchy function)를 이용하면 식 (2.12)를 가장 쉽게 증명할 수 있다.
[삼각 함수(trigonometric function)]
(2.13) 3. 특수 함수의 변환(transform of special functions)
[가우스 함수(Gaussian function)]
(3.1)[증명]
함수의 중심을 $\mu$ = $0$으로 설정한 가우스 함수(Gaussian function)의 정의를 식 (1.1)에 넣어서 정리한다.
(3.2)______________________________
형상 모수(形狀母數, shape parameter) $\sigma$가 약간 차이나지만, 가우스 함수는 푸리에 변환에 의해 모양이 변하지 않는 특성을 가지고 있다. 즉, 푸리에 변환의 항등원(identity element)은 가우스 함수가 된다.
4. 길쌈(convolution)
[그림 4.1] 구형 함수의 길쌈 예(출처: wikipedia.org)
[정의]
(4.1)길쌈(convolution)은 [그림 4.1]처럼 한 신호를 뒤집어서 다른 신호와 곱하기 때문에, 신호의 수신을 모형화할 때 매우 유용하게 사용된다.
[대수적 성질(algebraic properties)]
(4.2)
(4.3)식 (4.1)에 있는 길쌈에 대해 푸리에 변환을 적용하여 식 (4.3)의 첫째식을 증명한다.
(4.4)식 (4.4)의 결과에 식 (1.4)에 제시한 쌍대성을 적용한다.
(4.5)
(4.6)______________________________
[파르세발의 정리]
(4.7)길쌈 정리인 식 (4.3)의 둘째식에서 $\omega$ = $0$인 특별한 경우가 파르세발의 정리(Parseval's theorem)이다.
(4.8)______________________________
함수 $g(t)$가 $f(t)$와 같으면, 식 (4.7)은 다음과 같이 더 간략화될 수 있다.
(4.9)여기서 $f(t)$는 제곱 적분 가능한 함수(square-integrable function)이어야 한다.
[코쉬–슈바르츠 부등식(Cauchy–Schwarz inequality)] [5]
(4.10)[증명]
(4.11a)
식 (4.10)의 좌변과 우변에 있는 적분을 이중 적분(double integral)으로 바꾼다.
(4.11a)식 (4.11a)를 참고해서 함수 차이의 이중 적분을 고려한다.
(4.11b)______________________________
식 (4.10)에 제시한 주파수 영역의 부등식은 시간 영역에서도 동일하게 성립한다. 코쉬–슈바르츠 부등식은 원래 벡터 내적(inner product of vectors)을 위해 만든 부등식이다.
5. 급수 표현식(series representation)
[푸아송 합 공식]
(5.1)[증명]
(5.2)
연속으로 나열된 $f(t)$에 푸리에 역변환을 적용해서 정리한다.
(5.2)______________________________
식 (5.2)와 비슷한 방법을 사용하면, 주파수 영역에 대한 푸아송 합 공식도 증명할 수 있다.
(5.3)
[그림 5.1] 나이퀴스트–섀넌 표본화 정리의 원리(출처: wikipedia.org)
[나이퀴스트–섀넌 표본화 정리(Nyquist–Shannon sampling theorem)]
(5.4)여기서 표본화 각주파수(sampling angular frequency)는 $\omega_0$ = $2 \pi f_0$ = $2 \pi/T$ $\ge$ $2 \omega_b$, 표본화 주파수(sampling frequency)는 $f_0$ = $1/T$, $T$는 표본화 주기(sampling period), $\omega_b$는 각주파수 기준 신호의 대역폭(signal bandwidth)이며 $\omega_b$ = $2 \pi \cdot \text{BW}$, $\text{BW}$는 신호의 주파수 대역폭(frequency bandwidth); $f(t)$는 대역 제한(bandlimited)되어 $\text{BW}$ 이내에만 존재한다.
[증명]
(5.5)
[그림 5.1]에 있는 신호의 대역폭 $\omega_b$를 모두 포함하도록 $\omega_0 \ge 2\omega_b$로 정한 후, 주파수 영역의 이상적인 필터(ideal filter)를 $\operatorname{rect}(\omega/\omega_0)$로 정의한다. 이상적인 필터를 식 (5.3)의 좌변에 적용해서 푸리에 역변환을 한다.
(5.5)______________________________
표본화 주파수 $f_0$의 반은 나이퀴스트 주파수(Nyquist frequency) $f_n$ = $0.5 f_0$으로 부른다. 정상적인 표본화가 되려면 $f_n \ge \text{BW}$를 반드시 만족해야 한다. 비슷하게 대역폭의 2배는 나이퀴스트 변화율(Nyquist ratio)로 이름 붙인다. 그래서 나이퀴스트 변화율은 표본화 주파수보다 작아야[$2 \text{BW} \le f_0$] 표본화가 맞게 동작한다. 성공적인 표본화를 위한 부등식 조건 $f_n \ge \text{BW}$ 혹은 $f_0 \ge 2 \text{BW}$은 나이퀴스트 기준(Nyquist criterion)으로 명한다.
나이퀴스트–섀넌 표본화 정리는 보간(interpolation)에도 사용될 수 있어서 섀넌 보간 공식(Shannon interpolation formula)이라고도 한다. 나이퀴스트–섀넌 표본화 정리는 대역 제한 신호(band-limited signal)를 처리하는 새로운 방법을 제시한다. 연속 함수 $f(t)$를 알지 못하더라도, 이산화된 표본화 결과인 $f(mT)$만 알아도 원래 함수 $f(t)$를 복원할 수 있다. 현실에서는 표본화를 무한대로 할 수 없어서 식 (5.4)는 무한 급수가 아닌 유한 급수가 된다. 항이 개수가 유한개일더라도 표본화 정리는 $f(t)$를 잘 근사화하기 때문에, 표본화 정리는 섀넌 보간 공식으로도 부른다.
[기수 급수(cardinal series)] [3]
(5.6)여기서 $g(t)$는 $2 \pi$ 주기를 가지며 $G_m$ = $f(m)$, $f(t)$는 나이퀴스트–섀넌 표본화 정리에 따라 $\text{BW} \le 0.5$로 대역 제한된다.
[증명]
(5.7)
식 (5.6)의 첫째식 $g(t)$를 적분해서 새로운 함수 $f(t)$를 정의한다.
(5.7)식 (5.7)의 좌변에 $m$을 넣으면 $f(m)$ = $G_m$이 쉽게 유도된다.
______________________________
기수 급수(基數級數, cardinal series)는 각 항이 특정한 기수(基數, cardinal number)를 선택하거나 배제한다. 여기서 기수는 자연수 혹은 집합의 원소수(number of elements)를 뜻한다. 식 (5.6)의 결과에 $t$ = $m$을 넣으면 표본화 함수의 성질에 의해 각 항은 특정한 $m$을 뽑아내므로, 식 (5.6)은 정확히 기수 급수가 된다. 마찬가지로 식 (5.4)에 $T$ = $1$을 대입한 식은 식 (5.6)과 같아져서 기수 급수의 범주에 들어간다.
[최적 표본화 보간(optimal sampling interpolation, OSI)] [4]
(5.8)여기서 $f(t)$는 대역 제한된 신호, 푸리에 급수가 존재하는 수렴 인자(convergence factor) $\psi(t)$는 $\psi(0)$ = $1$인 성질을 가진다.
[증명]
(5.9)
매개변수 $\tau$는 아무값이나 넣을 수 있으므로, $\tau$ = $t$를 넣고 $\psi(0)$ = $1$을 대입한다.
(5.10)
길쌈(convolution) 형태인 함수 $f(t) \psi(\tau - t)$를 식 (5.4)에 넣는다.
(5.9)______________________________
무한 급수의 수렴 특성을 바꾸는 수렴 인자 $\psi(t)$는 제곱해서 적분이 존재한다면 어떤 함수든지 가능하다. 수렴 인자로 임의의 함수가 가능하기 때문에 더욱 간단한 식 (5.4)가 식 (5.8)보다 더 나아보인다. 이는 맞는 관점이지만 현실에서는 무한한 급수 합을 구하기는 불가능해서 유한 급수로 부분 합을 계산한다. 이 경우에 보간이 더 잘 되도록 수렴 인자를 택하면 나이퀴스트–섀넌 표본화 정리보다 더 개선된 보간을 정의할 수 있으므로, 식 (5.8)을 최적 표본화 보간(optimal sampling interpolation, OSI)으로 이름 붙인다.
[나이퀴스트–섀넌 표본화 정리의 연속화]
(5.10)여기서 $f(t)$의 각주파수 대역폭은 $\omega_b \le \pi$로 제한한다.
[증명]
(5.11)
함수 $f(t)$의 대역폭 조건으로 인해 $F(\omega)$는 $|\omega| \le \pi$ 범위에만 존재해서 식 (5.11)의 우변은 $F(\omega)$와 같다.
길쌈 정리를 사용해서 식 (5.10)의 우변을 푸리에 변환한다.
(5.11)______________________________
식 (5.10)으로 인해 표본화 함수는 $f(t)$를 적분해도 자기 자신이 그대로 나오는 항등적 특성을 가진다.
[정의]
(6.1)여기서 $\bar x$ = $(x_1, x_2, \cdots, x_n)$, $\bar k$ = $(k_1, k_2, \cdots, k_n)$, $\bar k \cdot \bar x$ = $k_1 x_1 + k_2 x_2 + \cdots + k_n x_n$이다.
[쌍대성(duality)]
(6.2)[길쌈 정의(definition of convolution)]
(6.3)여기서 $\bar x$ = $(x_1, x_2, \cdots, x_n)$, $\bar \chi$ = $(\chi_1, \chi_2, \cdots, \chi_n)$, $|d\bar \chi|$ = $d\chi_1 d\chi_2 \cdots d\chi_n$이다.
[길쌈 정리(convolution theorem)]
(6.4)[증명]
(6.5)
식 (4.4)와 비슷하게 다차원 푸리에 변환을 적용한다.
(6.5)다차원 푸리에 변환의 쌍대성인 식 (6.2)와 식 (6.4)의 첫째식을 써서 식 (6.4)의 둘째식도 증명한다.
(6.6)______________________________
7. 다양한 함수의 다차원 푸리에 변환
[가우스 함수(Gaussian function)]
(7.1)여기서 $|\bar x|$ = $\sqrt{x_1^2 + x_2^2 + \cdots + x_n^2}$, $|\bar k|$ = $\sqrt{k_1^2 + k_2^2 + \cdots + k_n^2}$이다.
(7.2)______________________________
[감쇠하는 지수 함수] [2]
(7.3)여기서 $\varepsilon > 0$이다.
(7.4)
(7.5)여기서 $|d \bar x|$ = $dx_1 dx_2 \cdots dx_n$, $\Gamma(\cdot)$는 감마 함수(gamma function)이다.
______________________________
가우스 함수와 동일하게 감쇠하는 지수 함수의 다차원 푸리에 변환도 실수이면서 항상 $0$보다 크게 된다.
[로렌츠–코쉬 함수(Lorentz–Cauchy function)]
(7.6)[증명]
식 (7.3)에 증명한 역변환 결과를 식 (6.2)에 대입해서 정리한다.
______________________________
(7.7)여기서 $K_\nu (\cdot)$는 제2종 변형 베셀 함수(modified Bessel function of the second kind)이다.
[증명]
(7.8)
식 (7.7)의 다차원 푸리에 변환을 위해 원래 식을 다음과 같은 적분으로 바꾼다.
(7.8)가우스 함수가 식 (7.8)에 나타나므로, 식 (7.1)을 이용해 다중 적분을 한다.
(7.9)식 (7.9)의 마지막 적분은 $K_\nu (\cdot)$의 적분 표현식이다.
(7.10)______________________________
8. 상관 관계(correlation)
[자기 상관(autocorrelation)과 교차 상관(cross-correlation)]
(8.1a: 자기 상관)
(8.1b: 교차 상관)여기서 $f(t), g(t)$는 복소 함수이다.
[상관 관계의 성질]
(8.2a)
(8.2b)만약 $f(t)$가 실수 함수라면, $f^*(t)$ = $f(t)$이므로 $R_{ff}(t)$ = $R_{ff}(-t)$를 만족한다. 이는 실수 함수 $f(t)$에 대한 자기 상관 $R_{ff}(t)$는 항상 우함수라는 뜻이다.
[푸리에 변환]
(8.3a)
(8.3b)여기서 $S_{ff}(\omega)$는 $f(t)$의 주파수별 전력 밀도를 나타내는 전력 스펙트럼 밀도(power spectral density, PSD)이다.
[증명]
상관 관계의 정의에서 $f^*(\tau - t)$ = $f^* [-(t-\tau)]$로 두고 길쌈 정리와 식 (1.6c)를 적용한다.
전력 스펙트럼 밀도 $S_{ff}(\omega)$를 모든 주파수에 대해 적분해서 전체 전력 $P_\text{tot}$를 정의한다.
(8.4)여기서 $P_\text{tot}$와 $S_{ff}(\omega)$의 단위는 각각 W와 W/Hz이다. 식 (8.3)의 중요한 응용은 그 유명한 확률 과정(random process)에 대한 위너–킨친 정리(Wiener–Khinchin theorem)이다. 스펙트럼 밀도 $S_{ff}(\omega)$의 결과가 에너지(energy)라면, $S_{ff}(\omega)$는 에너지 스펙트럼 밀도(energy spectral density, ESD)가 되고 그 단위는 J/Hz이다.
[참고문헌]
[1] P. M. Woodward and I. L. Davies, "Information theory and inverse probability in telecommunication," Proceedings of the IEE - Part III: Radio and Communication Engineering, vol. 99, no. 58, pp. 37–44, Mar. 1952.
[2] E. M. Stein and G. Weiss, Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, 1971.
[3] J. R. Higgins, "Five short stories about the cardinal series," Bull. Amer. Math. Soc., vol. 12, no. 1, pp. 45–89, Jan. 1985.
[4] J. Knab, "Interpolation of band-limited functions using the approximate prolate series (Corresp.)," IEEE Trans. Inf. Theory, vol. 25, no. 6, pp. 717–720, Nov. 1979.
[5] N. R. Rypkema, "A straightforward derivation of the matched filter," Technical Manuscript, Woods Hole Oceanographic Institution (WHOI), MA, USA, 2019. (방문일 2024-07-15)
[다음 읽을거리]
