[경고] 아래 글을 읽지 않고 "배열 안테나의 합성"을 보면 바보로 느껴질 수 있습니다.
[그림 1] 원소 안테나의 위상을 조정해서 자유롭게 빔 조향(beam steering)(출처: wikipedia.org)
배열 안테나(array antenna)는 원소 안테나(element antenna)의 여기(excitation) 진폭과 위상을 조절해서 주빔(main beam) 방향, 안테나 이득(antenna gain), 부엽 수준(sidelobe level, SLL), 격자엽(grating lobe) 등의 안테나 규격을 만족시킨다[1]. 원소 안테나의 진폭을 마음대로 바꾸기는 어려워서, 주로 원소 안테나의 위상을 위상 천이기(phase shifter)로 변경한다. 왜냐하면 증폭기로 진폭을 바꾸려면 가격이 비싸고 정밀한 제어가 어렵고, 가변 감쇠기(variable attenuator)는 RF 전력을 감소시켜서 선호되지 않기 때문이다. 그리하여 배열 안테나의 기본형으로 여기 진폭을 1로 둔 균일 선형 배열(uniform linear array, ULA)을 선택한다. ULA는 겉보기에 간단해 보이지만, 경우의 수 관점에서 ULA 설계는 매우 까다롭다. 예시로서 통상적인 위상 천이기의 위상 분해능(phase resolution)은 대략 6비트(6-bits) 혹은 5.6˚ 정도임을 고려한다. 그러면 50개 원소를 가진 ULA의 개별 위상을 바꾸는 경우의 수는 $(2^6)^{50}$ $\approx$ $10^{90}$이 나온다. 우주에 존재하는 모든 원자(atom) 개수를 약 $10^{80}$으로 예상하므로, 원소 개수가 $N$ = $50$인 ULA 설계는 우주 속의 모든 원자보다 많은 경우의 수를 가진다. 따라서 배열 안테나 설계는 단순한 최적화로는 달성할 수 없고 지능적 전략과 이에 걸맞는 최고 수준의 최적화 기법이 필요하다.
1. 쉘쿠노프 다항식 방법(Schelkunoff polynomial method) [2]
배열 인자(array factor, AF)의 영점(zero) 혹은 무효화(nulling)를 활용하는 방법으로 쉘쿠노프 다항식 방법(Schelkunoff polynomial method)이 있다. 이 방법은 특정 방항에서 오는 신호 간섭(signal interference)을 완전히 없애기 위한 무효 조향 혹은 널 조향(null steering)에 자주 쓰인다. 쉘쿠노프Sergei Alexander Schelkunoff(1897–1992)는 1936년쉘쿠노프 39세, 일제 식민지 시절에 쉘쿠노프 등가 원리(Schelkunoff equivalence principle)를 제안한 수학자 출신 전파 공학자이다.
쉘쿠노프 다항식 방법은 대수학의 기본 정리(fundamental theorem of algebra)에 기반을 두고 있다. 우리가 $M$개 각도에서 복사 패턴의 영점을 만들고 싶다면, 이 위치에서 근을 가지는 다항식 $P(z)$를 배열 인자 $\text{AF}(\theta)$로 활용한다.
(1.1)여기서 $z$ = $e^{j \psi}$, $\psi$ = $kd \cos \theta$, $k$ = $2 \pi \mathbin{/} \lambda$; 원소 안테나 개수는 $N$ = $M+1$, $d$는 원소 안테나의 간격, $z_n$ = $e^{j kd \cos \theta_n}$는 $\theta$ = $\theta_n$에서 복사 패턴이 0이 되는 영점, $a_n$은 $n$번 안테나의 여기 계수(excitation coefficient)이다. 식 (1.1)에 나온 $P(z)$를 전개한 후, 여기 계수 $a_n$을 각 $z^n$ 항의 계수로 정한다. 쉘쿠노프 다항식 방법은 영점을 설계하는 좋은 접근법이지만 원소 안테나의 진폭까지 조정해야 하는 약점이 있다. 최근에는 위상 배열 안테나(phased array antenna, PAA)처럼 위상만(phase-only) 조정해서 영점을 결정하는 방법이 최적화를 도구로 다양하게 연구되고 있다[3]–[5].
2. 이항 배열(binomial array) [6], [7]
이항 정리(binomial theroem)를 이용해서 배열 안테나의 복사 패턴이 거듭제곱으로 표현되게 함으로써 아예 부엽을 만들지 않는 배열은 이항 배열(binomial array)로 불린다. 각 원소 안테나가 가져야 되는 가중치는 이항 계수(binomial coefficient)와 연결된다.
(2.1)여기서 $\psi$ = $kd \cos \theta$, $a_0$ = $a_M$; 원소 안테나 개수는 $N$, 이웃한 원소 안테나간의 위상차 $\phi_0$은 0인 측면 발사 배열(broadside array)을 가정, 다항식의 차수는 $M$ = $N-1$, 이항 계수 ${}_MC_n$의 성질로부터 $a_n$ = $a_{M-n}$이다. 이항 배열의 배열 인자는 복사 패턴의 영점이 $z_i$ = $-1$로 동일한 식 (1.1)로 간주할 수 있다. 이와 같이 이항 배열은 배열 인자가 간단한 거듭제곱으로 표현되는 장점이 있지만, 각 여기 계수 $a_n$은 이항 계수 ${}_MC_n$을 따르기 때문에 중심과 양끝 원소 안테나의 진폭 차이는 매우 크다.
식 (2.1)에 제시한 배열 인자의 크기는 다음과 같다.
(2.2)
(2.3)여기서 $\psi$ = $0$에서 $\text{NAF}(\theta)$ = $1$이다. 이항 배열은 균일 선형 배열에 속하기 때문에, 원소 안테나간의 간격 $d$가 $\lambda$를 넘어가면 격자엽(grating lobe)이 반드시 생긴다. 이런 격자엽을 없앨 때는 꼭 $d < \lambda$ 조건을 지켜야 한다. 더불어 부엽(sidelobe) 자체가 없는 이항 배열은 $d \le \lambda/2$인 요건이 필요하다. 왜냐하면 $|\psi/2|$ $\le$ $\pi d / \lambda$ $\le$ $\pi/2$가 되어야 $\theta$에 따라 주빔이 작아지다가 커지지 않기 때문이다.
식 (2.3)을 써서 이항 배열의 반전력 빔폭(half power beamwidth, HPBW)을 구한다.
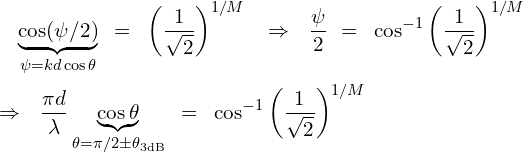(2.4a)
(2.4b)여기서 $\theta$ = $\pi/2 \pm \theta_\text{3dB}$, $\text{HPBW}$ = $\theta_\text{bw}$ = $2 \theta_\text{3dB}$이다. 식 (2.4b)는 정확하지만 실제로 쓰기는 복잡해서, $M \gg 1$인 조건으로 식 (2.4b)를 근사화한다.
(2.4c)여기서 $y$ = $\cos x$ $\approx$ $1-x^2 / 2$, $x$ = $\cos^{-1} y$ $\approx$ $\sqrt{2 (1-y)}$, $e^x$ $\approx$ $1-x$이다. 이항 배열의 방향도(directivity) $D$를 구하기 위해, 이 배열의 전체 복사 전력(total radiated power, TRP) $P_\text{rad}$를 계산한다.
(2.5a)만약 $\pi d / \lambda \le \pi/2$ 혹은 $d \le \lambda/2$라면 식 (2.5a)는 불완전 베타 함수(incomplete beta function) $B(x; a, b)$로 간략화된다.
(2.5b)불완전 베타 함수의 성질 $B(1; a, b)$ = $B(a, b)$를 쓰기 위해 $d$ = $\lambda/2$를 선택해본다.
(2.5c)여기서 $B(a, b)$는 베타 함수(beta function), $(\cdot)!!$는 이중 계승(double factorial)이다. 그러면 식 (2.5)를 방향도의 정의에 대입해서 $D$를 결정한다.
(2.6a)
(2.6b: $d$ = $\lambda/2$)이항 배열의 차수 $M$이 매우 커지면 스털링의 공식(Stirling's formula)을 써서 식 (2.6b)를 더 간단한 모양으로 바꿀 수 있다.
(2.6c)3. 돌프–체비셰프 배열(Dolph–Chebyshev array) [8]–[10]
복사 패턴의 빔폭(beamwidth)과 부엽(sidelobe)을 동시에 설계할 수 있는 기교로 돌프–체비셰프 배열(Dolph–Chebyshev array)이 널리 알려져 있다. 돌프–체비셰프 배열은 삼각 함수(trigonometric function)와 쌍곡선 함수(hyperbolic function)를 오가는 체비셰프 다항식(Chebyshev polynomial) $T_n(x)$의 특성을 이용한다. 체비셰프 다항식 $T_n(x)$는 $x$ = $[-1, 1]$에서는 삼각 함수처럼 변해서 함수값은 $-1$~$1$ 사이에 있으며, $x$가 $[-1, 1]$ 범위를 벗어나면 쌍곡선 함수(hyperbolic function)가 되어서 $|T_n(x)|$는 지수 함수처럼 빠르게 커진다.
(3.1)여기서 $x$ = $\cos \theta$이다.
[그림 3.1] 배열 원소의 배치 구조 (a) 홀수 개수 (b) 짝수 개수(출처: [11])
돌프–체비셰프 배열을 구성할 때 필요한 코사인 함수를 만들기 위해, 배열 원소 개수를 짝수와 홀수로 구분해서 배열 인자를 정의한다.
(3.2a)
(3.2b)
(3.3a)
(3.3b)여기서 $T_{K}(z_0)$ = $R_0$, $K$ = $N_\text{tot}-1$는 $2N$ 혹은 $2N-1$, $N_\text{tot}$는 원소 안테나의 총개수; $b_m$은 체비셰프 다항식 $T_K(x)$에서 $x^m$의 계수, $R_0$은 부엽 수준(sidelobe level, SLL)의 역수, 부엽 수준은 전기장 기준으로 $\text{SLL}$ = $1/R_0$, $\text{SLL (dB)}$ = $-20 \log_{10} R_0$이다. 식 (3.3)에 나온 $x^{2m}$과 $x^{2m-1}$은 다시 체비셰프 다항식으로 공식화할 수 있다.
(3.4)
[그림 3.2] 돌프–체비셰프 배열의 복사 패턴
[그림 3.2]는 식 (3.3)으로 선택한 배열 인자가 만드는 복사 패턴을 보여준다. 측면 발사 배열의 주빔 방향(main beam direction)인 $\theta$ = $90^\circ$에서 $u$ = $0$이 되어서 $x$ = $1$, $z$ = $z_0$가 나온다. 이 경우에 $T_{K}(z_0)$ = $R_0$으로 설정하기 때문에 다른 각도보다 값이 훨씬 큰 빔이 나오고 마땅히 주빔이 된다. 또한 주빔을 제외하고 큰 복사 패턴을 만드는 부엽(sidelobe)의 크기는 체비셰프 다항식의 특성으로 인해 1이다. 그래서 돌프–체비셰프 배열의 부엽 수준은 $\text{SLL}$ = $1/R_0$으로 계산된다. 부엽 수준의 역수 $R_0$를 알 때, 필요한 $z$ = $z_0$는 역쌍곡 함수(inverse hyperbolic function)로 유도한다.
(3.5a)
(3.5b)
(3.6)식 (3.5)와 비슷한 과정을 거쳐서 HPBW, $\theta_\text{bw}$ = $2 \theta_\text{3dB}$도 명시적으로 공식화한다.
(3.7a)
(3.7b)식 (3.7b)는 정확하지만 계산하기가 번거로워서 $R_0 \gg 1$ 및 $K \gg 1$로 가정해서 $\theta_\text{bw}$를 근사화한다[10].
(3.7c)여기서 $\cosh^{-1} x$ $\approx$ $\log (2x)$, $\cosh x$ $\approx$ $1 + x^2/2$, $\cos^{-1} x$ $\approx$ $\sqrt{2(1-x)}$, $\sin^{-1} x$ $\approx$ $x$; $L$ = $Kd$는 배열 안테나의 전체 길이이다. 측면 발사 배열의 방향도 $D_b$와 반전력 빔폭 $\theta_\text{bw}^b$의 관계식을 활용해서 돌프–체비셰프 배열의 방향도 $D$도 근사화한다.
(3.8a)
(3.8b)여기서 $K \gg 1$, $s_\text{hp}$ = 1.39155737825$\cdots$이다. 식 (3.8b)를 정확한 방향도에 더 근접시키기 위해, $K$를 조금씩 바꾼다. 그러면 다음 근사가 식 (3.8b)보다 좀더 나은 결과를 도출한다.
(3.8c)여기서 $N_\text{tot}$ = $K+1$은 원소 안테나의 총개수이다. 이상의 산출물을 종합해서 돌프–체비셰프 배열의 설계법을 확립한다.
[설계법]
- 목표로 하는 $D$와 $\text{SLL}$을 선택
- $R_0$ = $1/ \text{SLL}$ 계산
- 식 (3.8c)로 $N_\text{tot} d$를 얻음
- 식 (3.6)을 유지하면서 가능한 한 $N_\text{tot}$ = $K+1$은 작게 $d$는 크게 채택
- 식 (3.5b)로 $z_0$가 정해짐
- 식 (3.3)을 전개해서 $a_n$을 확정
______________________________
체비셰프 다항식이 있어서 돌프–체비셰프 배열은 설계가 까다롭지만, 근사 공식에 기반한 설계법으로 누구나 여기 계수 $a_n$을 거뜬히 획득할 수 있다.
[참고문헌]
[1] E. K. Miller, "Synthesizing linear-array patterns via matrix computation of element currents," IEEE Antennas Propag. Mag., vol. 55, no. 5, pp. 85–96, Oct. 2013.
[2] S. A. Schelkunoff, "A mathematical theory of linear arrays," Bell Syst. Tech. J., vol. 22, no. 1, pp. 80–107, Jan. 1943.
[3] R. L. Haupt, "Phase-only adaptive nulling with a genetic algorithm," IEEE Trans. Antennas Propag., vol. 45, no. 6, pp. 1009–1015, Jun. 1997.
[4] V. Zuniga, A. T. Erdogan, and T. Arslan, "Adaptive radiation pattern optimization for antenna arrays by phase perturbations using particle swarm optimization," NASA/ESA Conference on Adaptive Hardware and Systems, pp. 209–214, 2010.
[5] A. F. Morabito, A. Massa, P. Rocca, and T. Isernia, "An effective approach to the synthesis of phase-only reconfigurable linear arrays," IEEE Trans. Antennas Propag., vol. 60, no. 8, pp. 3622–3631, Aug. 2012.
[6] J. S. Stone, "Directive antenna array," US Patent No. 1643323, Sep. 1927.
[7] P. Apostolov, "An addition to binomial array antenna theory," Prog. Electromagn. Res. Lett., vol. 113, pp. 113–117, 2023.
[8] C. L. Dolph, "A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level," Proc. IRE, vol. 34, no. 6, pp. 335–348, Jun. 1946.
[9] R. S. Elliott, "Beamwidth and directivity of large scanning arrays," Microw. J., pp. 53–60, Dec. 1963.
[10] C. J. Drane, "Useful approximations for the directivity and beamwidth of large scanning Dolph-Chebyshev arrays," Proc. IEEE, vol. 56, no. 11, pp. 1779–1787, Nov. 1968.
[11] M. Khalaj-Amirhosseini, "Synthesis of low sidelobe level antenna arrays through only main lobe assumption," Sci. Rep., vol. 11, Nov. 2021, art. no. 22797.
댓글 없음 :
댓글 쓰기
욕설이나 스팸글은 삭제될 수 있습니다. [전파거북이]는 선플운동의 아름다운 인터넷을 지지합니다.