[경고] 아래 글을 읽지 않고 "오일러 각"을 보면 바보로 느껴질 수 있습니다.

[그림 1] 고전 오일러 각의 기하학적 정의(출처: wikipedia.org)
3차원 공간에 위치한 한 점을 수학적으로 표현하기는 매우 쉽다. 예를 들면, 좌표계 기반 벡터(vector)를 도입해서 3차원 위치를 3개의 숫자 나열인 $(x, y, z)$라 쓸 수 있다. 혹은 방향 코사인(direction cosine)을 이용해 $(x, y, z)$대신 각도 관점인 $(r \cos \alpha, r \cos \beta, r \cos \gamma)$가 될 수도 있다. 여기서 $r$은 원점에서 특정 점까지 거리, $\alpha, \beta, \gamma$는 방향 코사인의 각도이다. 하지만 [그림 1]처럼 3차원 공간상에서 한 점이 회전한 경우를 수식으로 표현하기는 매우 까다롭다. 여기서 파란색인 $xyz$ 좌표축이 고정된 기준이며, 빨간색인 $XYZ$ 좌표축이 $xyz$에서 $XYZ$로 가는 3차원 공간의 회전을 적용한 결과이다.

[그림 2] 3차원 공간에서 회전하는 강체(출처: wikipedia.org)

[그림 3] $z$축에 대한 기본 회전 행렬 ${\bf R}_{\hat z} (\theta)$(출처: wikipedia.org)
한번에 [그림 1]에 보인 여러 회전을 이해하기는 어렵기 때문에, 우리가 생각할 수 있는 가장 간단하고 쉬운 기본 회전(elemental rotation)부터 상기한다. 기본 회전은 $xyz$ 좌표축에 대한 회전을 뜻한다. 예를 들어, [그림 3]에 나타낸 2차원 $xy$평면의 회전을 본다. [그림 3]은 $z$축을 기준으로 점 $(x, yz)$를 $\theta$만큼 회전한 점이 $(x', y')$임을 보여준다. 각 $x,y,z$축에 대한 기본 회전 행렬(elemental rotation matrix)은 다음과 같이 공식화된다. 아래 결과의 증명은 삼각 함수의 합차 공식(angle sum and difference identity)을 쓰면 된다.
 (1a)
(1a) (1b)
(1b) (1c)
(1c)여기서 $\hat x, \hat y, \hat z$는 모두 단위 열 벡터(unit column vector), $\hat x$ = $[1~0~0]^T$, $\hat y$ = $[0~1~0]^T$, $\hat z$ = $[0~0~T]^T$이다. 식 (1)에 증명한 기본 회전 행렬을 도구로 3차원 공간상의 회전을 보여주는 [그림 1]을 이해한다. [그림 1]은 회전하지 않고 고정된 데카르트 좌표계(Cartesian coordinate system)인 $xyz$ 좌표계에서 시작해 3차원에서 임의로 회전한 또 다른 데카르트 좌표계인 $XYZ$ 좌표계로 바꾸는 절차를 보여준다. [그림 1]을 계속 보면 몇 가지 의문점이 생긴다. $xyz$ 좌표계에서 $XYZ$ 좌표계로 항상 갈 수 있을까? 기본 회전을 최소 몇 번 해야지 모든 회전을 다 표현할 수 있을까? 초보적이지만 근본적인 이 물음에 답한 최초의 수학자가 오일러Leonhard Euler(1707–1783)이다. 오일러는 1748년오일러 41세, 조선 영조 시절에 딱 3개의 각도인 $\alpha, \beta, \gamma$[이 각은 방향 코사인 각과는 완전히 다름]만 정의하면, [그림 1]의 알고리즘을 이용해 모든 3차원 회전을 표현할 수 있다는 성과를 제시했다. 이로 인해 [그림 1]에 나온 $\alpha, \beta, \gamma$를 오일러 각(Euler angle)이라 이름 붙인다. 오일러 각은 $\alpha, \beta, \gamma$ 대신 $\psi, \theta, \phi$를 쓰기도 한다. 오일러 각 $\alpha, \beta, \gamma$가 모든 3차원 회전을 나타내는 방식은 다음 절차를 따른다.
- 두 $xyz$와 $XYZ$ 좌표계의 일부인 $xy$와 $XY$평면[각각 파란색과 빨간색 원]이 만나 생기는 녹색 직선을 마디선 혹은 절점선(line of nodes)이라 명한다. 마디선의 방향은 벡터 $\bar N$으로 표기한다.
- $x$축이 벡터 $\bar N$과 만나도록 $z$축을 기준으로 $x$축을 각도 $\alpha$만큼 회전시켜서 $x'y'z$ 좌표계로 만든다. 수학적으로는 식 (1c)에 나온 ${\bf R}_{\hat z}(\alpha)$와 등가이다. 여기서 $x', y'$축은 $x, y$축이 회전된 결과이다. 벡터 $\bar N$은 마디선이라서 $x$축과 $\bar N$이 마주칠 수 있다.
- 이번에는 $z$축과 $Z$축이 딱 붙도록 $x'$축을 기준으로 $z$축을 $\beta$만큼 돌리는 ${\bf R}_{\hat x'}(\beta)$ 연산을 적용한다. 그러면 $x'y''Z$ 좌표축이 새롭게 만들어진다. 여기서 $y''$축은 $y'$축을 다시 회전시킨 상태를 뜻한다.
- $Z$축은 $XY$평면에 반드시 수직이므로, $Z$축에 수직인 $x', y''$축은 당연히 $XY$평면에 있다. 이 $x', y''$축이 $X, Y$축과 만나도록 $Z$축에 대해 $\gamma$만큼 선회시킨다. 이 연산은 ${\bf R}_{\hat Z}(\gamma)$가 된다.
- 최종적으로 $\alpha, \beta, \gamma$ 각도로 회전을 3번 하면, 고정된 기준인 $xyz$ 좌표계를 임의로 놓인 $XYZ$ 좌표계에 딱 맞출 수 있다.
오일러 각이 만드는 회전 연산 혹은 행렬 $\bf R$은 식 (1)에 제시한 기초 회전 행렬을 이용해서 다음과 같이 정의한다.
 (2a)
(2a) (2b)
(2b)여기서 $\bar {\bf u}$와 $\bar {\bf u}'$은 열 벡터(column vector), $\bar {\bf u}$ = $[x~y~z]^T$, $\bar {\bf u}'$ = $[x'~y'~z']^T$, $\bar {\bf u}'$은 벡터 $\bar {\bf u}$를 회전 행렬 $\bf R$에 따라 회전시킨 벡터, $\bar {\bf u}, \bar {\bf u}'$의 성분은 $xyz$ 좌표계로 기술한다.
우리가 적용하는 임의의 회전 연산은 식 (2b)와 같은 기본 회전 행렬의 곱이 일반적이지만 너무 많은 정보를 가져서 복잡해보인다. 그래서 회전의 기준인 회전축을 연산이 적용되는 순서에 따라 나열해서 식 (2b)를 $z$-$x'$-$Z$[회전축 $\hat z$, $\hat x'$, $\hat Z$ 순서로 기본 회전 행렬을 곱함] 혹은 $z$-$x'$-$z''$ 지향(orientation)으로 간략화한다. 더 간단하게 $z$-$x$-$z$로 기술하기도 한다. 회전축을 나열할 때는 먼저 적용하는 회전축부터 쓰기 때문에, 식 (2b)에 있는 회전 행렬의 오른쪽부터 왼쪽으로 회전축이 나와서 $z$-$x'$-$Z$가 된다. 회전축 시작은 각각 $x,y,z$축이 될 수 있고, 이 시작 회전축과 다른 2개의 축이 또 사용될 수 있어서 오일러 각을 정의하는 지향 나열(orientation sequence)은 총 6가지 경우가 있다.
- $z$-$x'$-$z''$, $z$-$y'$-$z''$, $x$-$y'$-$x''$, $x$-$z'$-$x''$, $y$-$z'$-$y''$, $y$-$x'$-$y''$

[그림 4] 테이트–브라이언 각의 기하학적 정의(출처: wikipedia.org)
[그림 1]에 나온 오일러 각은 쉽지만 $x,y,z$축 중에서 2개만 쓰는 방식이라서 다소 아쉽다. 이를 해결하기 위해 $x,y,z$축을 기준으로 모두 한 번씩 회전해서 임의의 $XYZ$ 좌표계를 맞추는 각도는 테이트–브라이언 각(Tait–Bryan angle)이라 정의한다. 각 좌표축의 회전을 한 번씩 모두 포함하는 방식이 기억하기 더 좋아서, 컴퓨터 그래픽스(computer graphics, CG) 분야에서는 3차원 임의 회전을 위한 각도로 테이트–브라이언 각을 주로 선택한다. 테이트–브라이언 각을 오일러 각이라 부르는 경우도 고려해서, [그림 1]과 같은 회전 연산에 쓰이는 각도는 특별히 고전 오일러 각(classic Euler angle) 혹은 정상 오일러 각(proper Euler angle)이라 명한다. 보통 고전 오일러 각에 $\alpha, \beta, \gamma$를 많이 쓰기 때문에, 테이트–브라이언 각은 주로 $\psi, \theta, \phi$로 표기한다. 테이트–브라이언 각를 제안한 테이트Peter Tait(1831–1901)는 사원수 역사에서 빼놓을 수 없는 소중한 물리학자이다. 맥스웰 방정식(Maxwell's equations)을 제안한 맥스웰James Clerk Maxwell(1831–1879)과 테이트는 동갑이며 동향인 죽마고우였다. 테이트는 사원수가 바탕인 고전적 맥스웰 방정식의 열렬한 지지자였고, 맥스웰이 죽은 후에도 사원수 기반 맥스웰 방정식을 지키려 피나게 노력했다. 하지만 1884년헤비사이드 34세, 조선 고종 시절에 헤비사이드Oliver Heaviside(1850–1925)가 어려운 사원수 대신 좌표계 기반 벡터(vector)를 쓰는 불손한 맥스웰 방정식을 제안해서 테이트를 매우 화나게 했다. 헤비사이드를 비난하며 사원수를 열심히 방어한 테이트의 분투에도 불구하고 연구자들은 헤비사이드의 맥스웰 방정식을 더 많이 활용했다. 테이트–브라이언 각의 또 다른 제안자인 수학자 브라이언George Bryan(1864–1928)도 보통이 아니다. 라이트 형제(Wright brothers)가 비행기를 날린 직후인 1911년브라이언 47세, 일제 식민지 시절에 브라이언은 곧 바로 비행기 자세 제어 이론을 성공적으로 개발했다. [그림 4]에서 테이트–브라이언 각인 $\psi, \theta, \phi$를 이용해 파란색 $xyz$ 좌표계를 임의로 놓인 빨간색 $XYZ$ 좌표계로 바꾸는 방법을 다음 순서로 제시한다.
- $z$축을 회전축으로 해서 $x$축을 $\psi$만큼 회전시켜서, 마디선 벡터 $\bar N$에 수직인 벡터 $\bar N^\perp$에 $x$축을 딱 맞춘다. 여기서 $\bar N$의 방향은 $xy$와 $YZ$평면이 만난 선과 같다. 그래서 $y$축은 $\bar N$에 평행이 되며, 회전한 결과는 $x'y'z$가 된다.
- 다음 단계로 $y'$축을 회전축으로 선택한 후, $x'$축을 $X$축에 맞도록 $\theta$만큼 돌린다. 두번째 회전으로 $Xy'z'$ 좌표계가 정의된다. $x'$축이 $X$축으로 움직일 수 있는 이유는 $y'$축에 기인한다. 즉, $y'$축은 $\bar N^\perp$과 $X$축에 수직이므로, $x'$축과 $X$축은 $y'$축을 법선 벡터로 하는 평면상에 있기 때문이다.
- 마지막으로 $X$축이 회전축이 되어서 $y'$축과 $Y$축이 만나도록 $\phi$ 각도만큼 회전시켜서 모든 축이 $XYZ$ 좌표계와 만나도록 한다. 여기서 $y'$축은 빨간색 원으로 표시한 평면에 놓여있어서 $X$축을 기준으로 회전하면 반드시 $Y$축과 만난다.
조금 전에 적용한 지향 나열은 회전축 적용 순서대로 $z$-$y'$-$X$[회전축 $\hat z$, $\hat y'$, $\hat X$ 순서로 기본 회전 행렬을 곱함] 혹은 $z$-$y'$-$x''$이 되므로, 테이트–브라이언 각은 모든 좌표축을 전부 사용해서 회전을 한다. 지향 나열 $z$-$y'$-$X$가 만드는 회전 행렬은 다음과 같다.
 (3)
(3)테이트–브라이언 각의 지향 나열은 서로 다른 3개 축을 순열(permutation)하는 6가지 경우라서 다음처럼 헤아린다.
- $z$-$x'$-$y''$, $z$-$y'$-$x''$, $x$-$y'$-$z''$, $x$-$z'$-$y''$, $y$-$z'$-$x''$, $y$-$x'$-$z''$
다만 식 (2b)와 (3)에서 보듯이 기본 회전 행렬을 식 (1)로만 쓰지 않고 회전한 좌표축을 다시 기준축[$\hat x'$, $\hat y'$, $\hat X$, $\hat Z$ 등]으로 삼아 재정의한 새로운 기본 회전 행렬도 필요하다. 이 과정은 매우 번거롭기 때문에, 실제 응용에서는 식 (1)처럼 회전축을 $xyz$ 좌표축으로만 고정한 기본 회전 행렬을 주로 쓴다. 이 두 회전 연산을 구별하기 위해, 식 (2b)와 (3)과 같이 회전한 좌표축을 다시 기준축으로 잡아 회전을 시키는 경우를 내재적 회전(intrinsic rotation)이라 한다. 내재적 회전과 다르게 회전하는 축을 항상 고정 좌표축[주로 $xyz$ 좌표축]으로만 선택하면 외재적 회전(extrinsic rotation)이라 이름 붙인다.

[그림 5] 회전 행렬 ${\bf R}_{\hat z}(\theta)$의 시각적 표현(출처: wikipedia.org)
쉬운 외재적 회전으로 복잡한 내재적 회전을 공식화하기 위해 [그림 5]와 같은 회전 행렬의 적용 과정을 재해석한다[2]. 회전 행렬의 원래 의미는 벡터 $\bar {\bf u}$를 회전 행렬 $\bf R$에 따라 회전시킨 결과가 행렬 곱 $\bar {\bf u}'$ = ${\bf R}\bar {\bf u}$라는 식 (2a)이다. 여기서 $xyz$ 좌표계는 움직이지 않고 고정되어 있으며, $\bar {\bf u}$와 $\bar {\bf u}'$은 모두 $xyz$ 좌표계에서 정의된다. 예를 들어, $\theta$ = $\pi/3$인 경우에 $\bar {\bf u}$ = $[1~0~0]^T$ = $\hat x$는 식 (1c)에 의해 $\bar {\bf u}'$ = $[1/2~\sqrt{3}/2~0]^T$ = $1/2\, \hat x + \sqrt{3}/2\, \hat y$로 변환된다. 다른 관점으로 회전 행렬 $\bf R$을 인식해서, 벡터 회전이 아닌 $x'y'z'$ 좌표(coordinate)를 $xyz$ 좌표로 바꾸는 방식도 상상할 수 있다. 좌표계를 간단히 부르기 위해 $xyz$와 $x'y'z'$ 좌표계를 $a$, $b$ 좌표계로 바꾼다. 좌상 첨자(left superscript)를 도입해서 식 (2a)의 벡터와 행렬이 정의된 좌표계를 명확히 한다.
 (4a)
(4a) (4b)
(4b)여기서 좌상 첨자는 벡터나 행렬의 왼쪽 어깨에 붙은 첨자, ${}^a \bar {\bf u}$는 좌표계 $a$의 기저 벡터(basis vector)에 대한 성분으로 정의한 벡터[${}^a \bar {\bf u}$ = $(x, y, z)$ = $x\, {}^a\hat x + y\, {}^a\hat y + z\, {}^a\hat z$이며 ${}^a\hat x, {}^a\hat y, {}^a\hat z$는 좌표계 $a$의 기저 벡터], ${}^{a}{\bf R}_{b \to a}$는 좌표계 $b$ 기준으로 기술한 성분을 좌표계 $a$의 성분으로 바꾸는 회전 행렬, $\hat {\bf x}_{b \to a}$는 좌표계 $b$의 기저 벡터 $\hat {\bf x}$를 좌표계 $a$의 기저 벡터 성분으로 표현한다는 뜻이다. 이전의 예시를 식 (4a)로 설명하면 같은 결과이지만 조금 다른 의미를 가진다. 먼저 벡터 ${}^{b}\bar {\bf u}$ = $\bar {\bf u}$ = $[1~0~0]^T$는 좌표계 $b$의 $x$방향 기저 벡터[= ${}^b \hat x$]만 가지고 있다. 이를 좌표계 $a$의 성분(component) 혹은 좌표(coordinate)로 표현하려면 회전 행렬 ${}^{a}{\bf R}_{b \to a}$에 ${}^{b}\bar {\bf u}$를 곱한다. 그러면 ${}^{a}\bar {\bf u}$ = $\bar {\bf u}'$ = $[1/2~\sqrt{3}/2~0]^T$는 좌표계 $a$의 기저 벡터 성분으로 표현되어 ${}^{a}\bar {\bf u}$ = $1/2\, {}^{a} \hat x + \sqrt{3}/2\, {}^{a} \hat y$가 나온다[2]. 더 쉽게 생각하면, 식 (2b)는 고정 좌표계에서 입력 벡터를 회전시키는 회전기(rotator)이며, 입력과 출력 벡터는 회전하지 않는 고정 좌표계에서 정의된다. 반면에 식 (4b)는 벡터를 돌리지 않고 좌표계 $b$에 놓인 입력 벡터를 좌표계 $a$ 기준으로 해석하는 번역기(translator)로 작동한다. 회전 행렬을 회전기로 쓸지 번역기로 쓸지는 전적으로 사용자 몫이다.
회전 행렬을 식 (4b)로 생각해 식 (2b)의 회전 행렬을 고정된 좌표계 $a$의 외재적 회전으로 재정의한다. 유도에 앞서 식 (2b)로 정의한 오일러 각에 의해 좌표계는 $a \to b \to c \to d$ 순서로 변환된다고 가정한다. 좌표계 $a$ 혹은 $xyz$는 회전 연산과 무관하게 고정된다. 첫 단계로 좌표계 $a$의 기본 회전 행렬을 식 (4b)처럼 만든다.
 (5)
(5)식 (2b)에 나온 ${\bf R}_{\hat x'}(\beta)$는 좌상 첨자를 써서 다소 복잡한 ${}^a{\bf R}_{c \to b}$로 표현한다. 이는 좌표계 $c$의 성분을 좌표계 $b$의 기저 벡터 기준으로 번역할 때에 최종 결과는 좌표계 $a$의 기저 벡터 성분으로 공식화한다는 뜻이다. 이 개념에 식 (5)를 넣어서 ${\bf R}_{\hat x'}(\beta)$를 고정 좌표계 $a$의 기본 회전 행렬 곱으로 분해한다.
 (6a)
(6a) (6b)
(6b) (7)
(7) (8)
(8)식 (8)을 보면 내재적 회전 곱과 외재적 회전 곱은 각각 오른쪽에서 왼쪽, 왼쪽에서 오른쪽으로 서로 반대된 순서로 적용된다. 그래서 오일러 각에 대해 내재적 회전으로 정의한 지향 나열 $z$-$x'$-$z''$는 외재적 회전으로는 $z$-$x$-$z$가 된다. 특별한 고민없이 비슷하게 테이트–브라이언 각을 내재적 회전으로 정의한 식 (3)도 외재적 회전으로 바꾼다.
 (9)
(9)여기서 지향 나열 $z$-$y'$-$x''$은 $x$-$y$-$z$로 변한다.

(a) 이동하는 비행체

(b) YPR 연산 적용
[그림 6] YPR인 요, 롤, 피치를 이용한 비행체의 방향 전환(출처: wikipedia.org)
지향 나열 $z$-$y'$-$x''$(내재적 회전) 혹은 $x$-$y$-$z$(외재적 회전)는 워낙 유명해서 각 회전 연산에 이름이 붙어있다. 좌표축 $z, y, x$에 대한 회전은 각각 요(yaw), 피치(pitch), 롤(roll), 약자로는 YPR이라 부른다. 요는 통통배가 흔들거리며 제자리 회전하는 모습, 피치는 투수(pitcher)가 공을 던지는 행동, 롤은 돌림판(roller)의 회전을 표현하는 용어이다. 그래서 요, 피치, 롤을 그대로 직역하면 흔들기, 던지기, 굴리기이다. [그림 6]은 비행체가 $x$축을 따라 날아갈 때 회전 연산을 적용해서 비행체의 방향을 바꾸는 모양을 보여준다. 여기서 $z$축은 중력이 작용하는 방향의 반대로 놓이며, $\psi, \theta, \phi$는 식 (3)처럼 요, 피치, 롤의 각도이다. 비행체의 방향 변경에 쓰이는 회전 연산도 요, 피치, 롤이라 할 수 있지만, 비행체 이동을 더 강조하기 위해 YPR 대신 헤딩(heading), 고도(elevation), 뱅크(bank)로 바꿀 수 있다. 헤딩은 축구에 나오는 헤딩(heading)과 같은 뜻이며, 우리가 진행하는 머리 방향을 바꾼다. 고도는 당연히 비행체의 높이(elevation)에 변화를 주고, 뱅크는 선회할 때 경사면(bank) 영향처럼 비스듬하게 날아가게 한다. 그렇다면 헤딩, 고도, 뱅크는 향하기, 고도, 비스듬으로 번역할 수 있다.
외재적 회전으로 표현한 오일러 각 결과인 식 (8)을 계산해서 오일러 각의 회전 행렬 $\bf R$을 공식으로 만든다.
 (10)
(10) (11)
(11)여기서 $\hat z$ = $[0~0~1]^T$, $\hat z'$ = $[z_1'~z_2'~z_3']^T$이다. 벡터 $\bar N$은 마디선을 나타내고 있어서 $\hat z, \hat z'$에 항상 수직이어야 한다. 따라서 두 벡터 $\hat z, \hat z'$의 법선 벡터를 찾는 외적(outer product)을 써서 식 (11)처럼 $\bar N$을 구한다. 식 (10)과 (11)을 조합해서 $\alpha, \beta, \gamma$의 관계를 손쉽게 만들어낸다.
 (12)
(12)여기서 $\hat x$ = $[1~0~0]^T$, $\hat y$ = $[0~1~0]^T$, $\hat x'$ = $[x_1'~x_2'~x_3']^T$, $\hat y'$ = $[y_1'~y_2'~y_3']^T$, $\bar N \cdot \hat y'$ = $\hat z \cdot (\hat z' \times \hat y')$ = $-x_3'$, $\bar N \cdot \hat x'$ = $\hat z \cdot (\hat z' \times \hat x')$ = $y_3'$, $\operatorname{atan2}(\cdot)$는 주치(principal value)가 $(-\pi, \pi]$ 혹은 $[0, 2 \pi)$인 2변수 탄젠트 역함수(2-variable arctangent function), $\gamma$는 $\bar N$에서 $x'$축으로 잰 각도라서 ($-$) 부호가 붙는다. 각도 $\beta$는 코사인 역함수로 구해져서 $\beta$의 주치는 $[0, 2 \pi)$가 아닌 반이 줄어든 $[0, \pi]$가 된다. 이와 비슷한 특성은 구 좌표계(spherical coordinate system)의 각도인 $\theta, \phi$에서도 나타난다. 최종 회전 행렬 $\bf R$에서 $\beta$ = $0, \pi$인 경우는 특성이 약간 이상해진다.
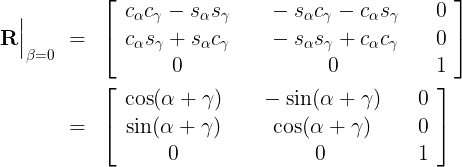 (13a)
(13a) (13b)
(13b)오일러 각 $\alpha, \gamma$가 각각 독립적으로 움직이지 않고, $\alpha \pm \gamma$와 같이 각도의 합이나 차로 변해서 오일러 각이 가진 자유도(degree of freedom) 하나가 사라진다. 오일러 각 자체는 문제가 없지만, 제어할 수 있는 자유도가 하나 사라져서 강체의 자세 조정에 문제가 생기는 현상을 전통적으로 짐벌 잠금(gimbal lock)으로 부른다.

(a) 짐벌의 좌표계
[그림 7]에 보이는 짐벌 혹은 수평 유지기(gimbal)는 복잡하게 운동하는 강체의 수평을 맞출 때 사용하는 두 개의 고리이다. 짐벌이라는 말이 조금 어렵지만 어원을 생각하면 다소 수월하게 접근할 수 있다. 짐벌과 같은 어원을 가진 영어는 제미니(Gemini)이다. 제미니는 별자리중 쌍둥이 자리를 뜻해서, 짐벌에도 쌍둥이라는 개념이 있다. [그림 7]에서 명확하듯이, 짐벌에서 말하는 쌍둥이는 비슷한 모양으로 만든 2개의 고리를 가리킨다. 짐벌의 두 고리를 연결하는 축이 [그림 1]의 마디선 벡터인 $\bar N$이며, 안과 바깥 고리의 좌표계는 각각 $X, Y, Z$축과 $x, y, z$축을 [그림 1]과 같이 나타낸다. 두 고리의 $z$와 $Z$축을 평행하게 둔 경우를 $\beta$ = $0$이라 하면, $\beta$의 주치는 식 (12)와 같이 $[0, \pi]$가 된다. 조금 다르게 $z$와 $Z$축을 수직으로 만든 상태를 $\beta$ = $0$이라 할 수 있다. 이때는 $\beta$가 $[-\pi/2, \pi/2]$로 변하고, 짐벌 잠금은 $\beta$ = $\pm \pi/2$에서 생긴다. 짐벌 잠금으로 인해 생기는 제어 문제는 [그림 7(c)]에서 관찰할 수 있다. 두 고리가 같은 평면에 있으면, $\alpha, \gamma$를 아무리 바꾸어도 자세는 한 방향으로만 변한다. 각도 $\beta$가 짐벌 잠금 근처에 있어도 문제가 생긴다. 예를 들어, $\beta \approx 0$인 경우에 $z_3' \approx 1$, $z_1' \approx 0$, $z_2' \approx 0$, $x_3' \approx 0$, $y_3' \approx 0$ 정도로 근사화할 수 있다. 이 조건에서 $Z$축이 $z$축을 살짝만 넘어도 식 (12)에 의해 $\alpha, \gamma$가 불연속적으로 변해서 제어에 문제가 생길 수 있다. 구 좌표계에서 위치 벡터가 $\theta$ = $0, \pi$인 점을 넘을 때에 $\phi$가 불연속적으로 변하는 사례와 매우 비슷하다. 짐벌 잠금이 생긴다고 해서 오일러 각 자체가 문제가 있지는 않다. 식 (12)처럼 $\alpha, \beta, \gamma$를 삼각 함수의 역함수로 정의해서 나오는 문제라서 사원수(quaternion) 등으로 해결할 수 있다.
테이트–브라이언 각인 [그림 4]에서 $xy$와 $YZ$평면이 만드는 $\bar N$을 구할 때는 두 평면의 법선 벡터의 외적을 쓰면 된다. 이와 같은 방식은 [그림 1]에 나온 $\bar N$을 구하기 위해 평면의 법선 벡터 $\hat z, \hat z'$을 쓴 식 (11)과 동일하다.
 (14)
(14)여기서 $X$축의 단위 벡터는 $\hat x'$ = $[x_1'~x_2'~x_3']^T$이다. 식 (12)와 비슷하게 기하학을 써서 테이트–브라이언 각 $\psi, \theta, \phi$를 차례로 유도한다.
 (15)
(15)여기서 $\hat y'$ = $[y_1'~y_2'~y_3']^T$, $\hat z'$ = $[z_1'~z_2'~z_3']^T$, $\theta$는 $\bar N$을 기준으로 반대 방향으로 회전해서[회전축 $\bar N$을 기준으로 오른손 법칙으로 돌리는 각과 반대로 $\theta$가 회전] 부호를 $(-)$로 붙인다. 오일러 각 $\beta$처럼 각도 $\theta$도 주치가 $[-\pi/2, \pi/2]$로 줄어든다.
[참고문헌]
[1] 박성수, 방향코사인행렬, 오일러각, 그리고 쿼터니언, 딥웨이브, 2020.
[2] D. Plein, "Extrinsic & intrinsic rotation: do I multiply from right or left?," Medium, May 2022. (방문일 2023-09-17)
[다음 읽을거리]



 (1)
(1) (2)
(2)
 (3a)
(3a) (3b)
(3b) (4)
(4) (5)
(5) (6)
(6) (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12)
 (1.3)
(1.3)

 (1.5b)
(1.5b) (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6)


