[경고] 아래 글을 읽지 않고 "수치 미분"을 보면 바보로 느껴질 수 있습니다.

[그림 1] 여러 가지 차분 방법(출처: wikipedia.org)
미분 공식을 이용해서 어떤 종류의 함수든지 미분을 할 수 있지만, 컴퓨터를 사용해서 미분을 근사할 때는 다음과 같은 차분(差分, difference)을 사용한다.
 (1)
(1)여기서 $x$의 차분 $h$가 0으로 한없이 접근하면 차분은 미분이 된다. 식 (1)은 현재점 $x$를 기준으로 전방에 위치한 $x+h$의 함수값으로 차분을 구해서 전방 차분(forward difference) $\Delta_f$라 부른다. 이 차분과 $h$의 나눗셈은 차분 몫(difference quotient)이면서 미분의 근사 혹은 수치 미분(numerical differentiation)이 된다. 비슷하게 후방에 있는 $x-h$ 점에서 시작해 구한 차분은 당연히 후방 차분(backward difference) $\Delta_b$가 된다.
 (2)
(2)혹은 점 $x$의 앞과 뒤에 있는 함수값의 차분을 써서 중앙에서 구한 차분을 만들기도 한다.
 (3a)
(3a)여기서 첫째식의 분자는 중앙 차분(central difference) $\Delta_c$, 둘째식의 분자는 대칭 차분(symmetric difference) $\Delta_s$로 이름 붙인다. 중앙 차분에서 중앙값 $y(x)$는 양쪽 끝값의 평균으로 근사하기도 한다. 이 근사를 쓰지 않으려면 함수 관계로 $y(x)$를 직접 계산하거나 문제 조건에서 $y(x)$를 예측해야 한다.
 (3b)
(3b)반면에 대칭 차분은 $y(x)$를 이미 알고 있어서 식 (3b)가 필요없다. 왜냐하면 간격 $h$를 기준으로 $y(x-h)$, $y(x)$, $y(x+h)$는 이미 주어지기 때문이다.
전방 차분 몫의 오차는 테일러 급수(Taylor series)를 이용해서 쉽게 구할 수 있다.
 (4)
(4)여기서 $y$ = $f(x)$, $h \ll 1$이다. 식 (4)는 일종의 근사라서 마음에 쏙 들지 않는다. 미분에 대한 평균값의 정리(mean value theorem)에서 출발해 식 (4)를 더 엄격하게 표현한다[1].
 (5a)
(5a) (5b)
(5b)여기서 $x \le \xi \le x+h$이다. 식 (5a)의 결과는 제1차 잉여항(remainder term)을 포함한 테일러 급수(Taylor series)와 동일하다. 비슷한 방식으로 대칭 차분 몫의 오차도 공식화된다.
 (6)
(6)테일러 급수를 이용한 분석에 따라, $y$ = $f(x)$가 부드럽게 변하는 경우에 중앙이나 대칭 차분 몫이 전방이나 후방 차분 몫보다 훨씬 더 미분값에 가깝다.

[그림 2] 차분 $h$에 대한 수치 미분 오차의 변화(출처: wikipedia.org)
이 시점에서 고민할 부분은 $h$의 선택이다. 미분 정의에 가까우려면 가능한 한 $h$를 작게 택해야 한다. 하지만 현실에서 $h$를 얼마나 작게 할 수 있을까? 여기서 말하는 현실은 컴퓨터로 계산할 때이다. 수치 계산에는 기계 엡실론(machine epsilon)이라는 나름 창의적인 개념이 있다. 0이 아닌 양수인 기계 엡실론 $\varepsilon$은 수치 계산 관점에서 $1+\varepsilon$과 $1$을 다르게 만드는 가장 큰 실수이다. 수학에서는 당연히 $1+\varepsilon$과 $1$이 다르지만, 컴퓨터는 유한한 유효 숫자로 이진수를 만들어서 계산하므로 컴퓨터 구조마다 고유한 기계 엡실론이 존재한다.

[그림 3] 이중 정밀도의 비트 분포(출처: wikipedia.org)
예를 들어, 요즘 사용되는 컴퓨터는 실수 계산을 할 때에 기본적으로 이중 정밀도(double precision)인 64 비트(bit)를 사용한다. 예전에는 단일 정밀도인 32 비트를 주로 사용했다. 이중 정밀도의 비트 분포는 [그림 3]에서 볼 수 있다. C 언어의 실수 자료형(data type)에서 단일 정밀도는 float, 이중 정밀도는 double로 칭한다. [그림 3]에 따라 컴퓨터가 쓰는 이중 정밀도 실수가 가진 유효 숫자(有效數字, significant figure)는 52 비트를 가진다. 이 52 비트는 항상 1.으로 시작하는 이진 소수의 유효 숫자라서 가장 낮은 소수 자리수는 소수점 이하 52번째이다. 그래서 지수(exponent)가 0인 이중 정밀도 실수에서, 1과 가장 가까운 이진수는 1.0000000000000000000000000000000000000000000000000001이 된다. 따라서 이중 정밀도의 기계 엡실론은 $\varepsilon$ = $2^{-52}$ = 2.22044604925031$\cdots \times 10^{-16}$이다. 그러면 $h$ = $\varepsilon$인 경우가 가장 최적의 수치 미분을 얻게 하는가? [그림 2]의 결과를 보면, 우리 예상과는 다르게 $\varepsilon$보다 훨씬 큰 $h$를 선정해야 한다. 수치 미분의 오차를 최대로 줄이는 $h$를 구하기 위해, 컴퓨터로 함수를 계산할 때에 필연적으로 나타나는 반올림 오차(round-off error)를 기계 엡실론 개념으로 근사화한다.
 (7)
(7)여기서 $\varepsilon_1$ = $\varepsilon_1(x)$, $\varepsilon_2$ = $\varepsilon_2(x, h)$, $\widetilde{f}(x)$는 $x$에서 계산한 반올림 오차를 반영한 함수값, $f(x)$는 정확한 함수값이다. 식 (7)을 식 (1)에 대입해서 반올림 오차를 가진 수치 미분을 구한다[1].
 (8)
(8)여기서 $h$는 매우 작아서 $f(x+h)$ $\approx$ $f(x)$이다. 식 (8)을 다시 식 (5b)에 넣어서 수치 미분의 오차 $E (h)$와 최대 오차 $E_{\max}(h)$를 표현한다.
 (9)
(9)여기서 $|\varepsilon_2 - \varepsilon_1| \le 2 \varepsilon$, $\varepsilon$는 이중 정밀도의 기계 엡실론, $f(\xi)$와 $f^{(2)}(\xi)$는 $x \le \xi \le x+h$에서 거의 상수이면서 0은 아니라고 가정한다. 식 (9)의 둘째식을 미분해서 0이 되는 값이 바로 최적의 $h$인 $h_\text{opt}$이다[1].
 (10)
(10)함수 $f(x)$마다 $h_\text{opt}$는 다르지만, 편하게 근사하기 위해 보통 $h_\text{opt}$ $\approx$ $2 \sqrt{\varepsilon}$ $\approx$ $3 \times 10^{-8}$으로 생각한다. 이 결과는 [그림 2]에 보이는 $h_\text{opt}$를 잘 설명한다.
1. 기본(basics)
[정의]
 (1.1)
(1.1)독립 변수 $x$의 차분인 $h$가 같은 간격으로 변하는 경우의 차분을 정의하기 위해 식 (1.1)을 빈번하게 사용한다.
[선형 사상(線型寫像, linear mapping)]
 (1.2)
(1.2)모든 종류의 차분에 대해 선형 사상이 항상 성립한다.
[곱의 차분]
 (1.3a)
(1.3a) (1.3b)
(1.3b)여기서 $f_{m+0.5}$ = $(f_m + f_{m+1})/2$, $f_{m-0.5}$ = $(f_{m-1} + f_{m})/2$이다.
[증명]
함수 곱을 식 (1.1)에 넣고 정리해서 식 (1.3)을 증명한다. 나머지 차분도 동일하게 접근할 수 있다.
 (1.4a)
(1.4a) (1.4b)
(1.4b)______________________________
식 (1.3b)의 마지막식은 차분 연산에 빈번하게 쓰이는 유용한 공식이다. 다만 좌변과 완벽히 같지는 않기 때문에, $h$가 0에 매우 가깝다는 조건이 필요하다.
[참고문헌]
[1] K. Mørken, Chapter 11. Numerical Differentiation, Numerical Algorithms and Digital Representation, University of Oslo, Norway, Nov. 2010. (방문일 2023-04-16)
[2] F. B. Hildebrand, Introduction to Numerical Analysis, 2nd ed., New York, USA: Dover Publications, 1987.



 (1a)
(1a) (1b)
(1b) (1c)
(1c) (2a)
(2a) (2b)
(2b)
 (3)
(3)
 (4a)
(4a)
 (5)
(5) (6a)
(6a) (6b)
(6b)
 (8)
(8) (9)
(9)


 (11)
(11) (12)
(12)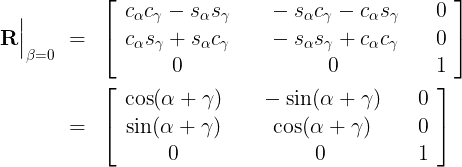 (13a)
(13a) (13b)
(13b)

 (14)
(14) (15)
(15)