1. 적분법의 의미
2. 테일러 급수
3. 미분 방정식의 의미
4. 지수 적분
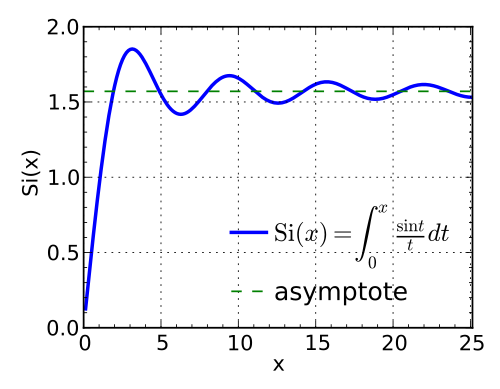
[그림 1] 사인 적분(출처: wikipedia.org)
피적분 함수가 사인 함수(sine function)로 구성된 적분(integration) 중에서 가장 유명한 적분은 아마 다음의 사인 적분 $\text{Si}(\cdot)$(Sine integral)이다.
(1)
사인 적분이 중요한 이유는 피적분 함수가 표본화 함수(sampling function) $\text{Sa}(x)$이기 때문이다.
(2)
사인 적분의 의미를 찾기 위해 표본화 함수로 만든 다음 적분을 고려한다.
(3)
(4)여기서 $\operatorname{rect}(\cdot)$는 구형 함수(rectangular function) 혹은 사각 함수, $\mathfrak{F}[f(t)]$는 $f(t)$의 푸리에 변환(Fourier transform)이다. 식 (3)과 (4)처럼 표본화 함수의 적분 구간이 무한대이면 적분값을 정확히 구할 수 있다. 다만 식 (3)의 증명에는 고급 개념인 푸리에 변환의 쌍대성(duality)이 필요하다. 만약 적분 구간이 식 (1)처럼 유한하다면 어떻게 될까? 여기에 대한 답이 바로 식 (1)의 사인 적분이다. 식 (1)의 적분값은 사인 함수의 테일러 급수(Taylor series)를 이용해 쉽게 구할 수 있다.
(5: 삼각 함수의 합차 공식)
(6)
식 (6)은 사인 함수에 대한 적분 결과이므로 식 (6)의 무한 급수(infinite series)는 모든 영역에서 수렴한다. 하지만 이 부분은 수학적으로만 맞는 말이고 실제 수치 계산에서는 맞지 않다. $x$가 커지면 무한 급수의 항이 빠르게 커져 매우 많은 항을 합쳐 주어야 수렴하게 된다. 그래서 수치 계산을 효율적으로 하려면 사인 적분의 점근식(asymptote)이 필요하다. 사인 적분의 점근식을 구하기 위해 식 (4)와 부분 적분(integration by parts)을 이용한다.
(7)
식 (7)의 과정을 계속 반복하면 다음 결과식을 얻을 수 있다.
(8)
다음으로 사인 적분이 만족하는 미분 방정식(differential equation)을 찾아본다. 찾는 법은 비교적 간단하다. 사인 적분을 미분하여 계수를 서로 비교하면 쉽게 관계되는 미분 방정식을 만들 수 있다.
(9)
세 번 미분한 관계식을 한 번과 두 번 미분한 관계식과 연립할 수 있어서 다음 미분 방정식의 해는 사인 적분이 된다.
(10)
어차피 적분해서 식 (2)의 표본화 함수가 나오면 식 (10)의 미분 방정식을 만족하므로, 새로운 사인 적분을 다음처럼 정의할 수 있다.
(11)
식 (7)을 참고하면 식 (11)의 정의는 점근식 유도에 매우 유용하다. 사인 적분 간의 관계식은 다음과 같다.
(12)
식 (4)에 소개한 이상 적분(improper integral)은 신기하게도 수렴한다. 하지만 아래 절대값을 가진 적분은 발산한다[2]. 식 (4)와 (5)의 예는 절대값 유무에 따라 적분값이 수렴 혹은 발산하는 좋은 예이다.
(13)
식 (13)의 증명은 의외로 간단하다. 식 (13)의 적분 구간 일부를 다음과 같은 수열로 표현한다.
(14)
수열 $a_n$은 조화 급수(harmonic series)의 항보다 항상 크고 조화 급수는 발산하므로 식 (13)은 발산한다.
1. 기본(basics)
[대칭성(symmetry)]
(1.1)
(1.2)[증명]
식 (11)에서 적분 구간을 바꾸면 다음과 같다.
(1.3)______________________________
2. 특정값(specific value)과 극한(limit)
[표본화 함수(sampling function)]
사인 적분의 피적분 함수인 표본화 함수의 영점(zero)은 $x$ = $0$을 제외한 $\sin(x)$ = $0$에서 구한다.
(2.1)비슷하게 표본화 함수의 극값이 나오는 극단점(極端點, extreme point or local extremum point)은 다음과 같다.
(2.2)[표 2.1] 표본화 함수의 극단점, $p_m$(출처: wolframalpha.com)
| 극단점, $p_m$ | 극단점의 계산값 |
|---|---|
| $p_0$ | 0 |
| $p_1$ | 4.49340945790906417530788092728032208222$\cdots$ |
| $p_2$ | 7.72525183693770716419506893306298662638$\cdots$ |
| $p_3$ | 10.9041216594288998271487027901886838721$\cdots$ |
표본화 함수의 극단점은 $x$ = $0$을 제외하고는 쉽게 구할 수 없어서, 수치 해석으로 근 찾기(root searching or finding)를 해야 한다. 우함수(even function) 특성으로 인해 극단점은 $x$ = $\pm p_m$에서 생긴다. 또한 $x$가 커짐에 따라 $p_m$ = $\pi/2 + m \pi$에 수렴한다.
[그림 2.1] 표본화 함수의 제곱이 1/2(출처: wolframalpha.com)
표본화 함수의 제곱이 1/2로 나오는 $x$값은 공학 분야에 빈번하게 쓰인다.
(2.3)예를 들면, 안테나의 복사 패턴을 수치로 보여주는 빔폭(beamwidth) 정의에 식 (2.3)이 유용하게 사용된다.
3. 이상 적분(improper integration)
[표본화 함수(sampling function)]
(3.1)[증명]
부분 적분을 먼저 적용한 후에 식 (4)를 가져온다.
(3.2)______________________________
표본화 함수는 특이하게도 자기 자신의 적분과 제곱한 적분의 결과가 서로 동일하다.
[참고문헌]
[다음 읽을거리]
1. 코사인 적분
[2] Andrés Caicedo, "175 - The sine integral," Teaching Blog, 2008.
[3] J. D. Mahony, "On alternative evaluation of the integrals $\text{Cin}(z)$ and $\text{Si}(z)$," IEEE Antennas Propag. Mag., vol. 56, no. 2, pp. 156–160, April 2014.
[다음 읽을거리]
1. 코사인 적분
(1)
(2)
(3)
(5)
(6)
(7)
(8)
