전자파의 운동량(Momentum of Electromagnetic Wave)

[경고] 아래 글을 읽지 않고 "전자파의 운동량"을 보면 바보로 느껴질 수 있습니다.
1. 뉴턴의 운동 법칙
2. 에너지의 개념
3. 균일 평면파의 의미
4. 포인팅의 정리

[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.

파동의 에너지와 운동량 관계식을 이용하면 전자파의 운동량(momentum of electromagnetic wave)을 정의할 수 있다.

                           (1)

식 (1)에서 전자파의 속도는 $c$로 일정하기 때문에 전자파가 전달되는 속도 방향 운동량 $p_c$는 다음으로 쓸 수 있다.

                           (2)

여기서 $v$는 우리가 적분하려는 체적(volume)이다. 식 (2)의 좌변에 있는 운동량도 우변의 전자파 에너지 밀도(energy density of electromagnetic wave)처럼 단위체적당 운동량 $\mathfrak{p}_c$로 바꾸면 다음을 얻는다.

                           (3)

식 (3)을 간략화하기 위해 우리가 생각하는 전자파를 균일 평면파(uniform plane wave)로만 한정하자. 먼저 평면파의 다음 성질을 기억하자.

                         (4)

여기서 $\bar k$는 파수 벡터(wavenumber vector)이다. 식 (4)를 식 (3)에 대입하면 다음을 얻는다.

                         (5)

여기서 $\bar k$ = $k_0 \hat k$, $k_0$ = $\omega \sqrt{\mu_0 \epsilon_0}$, $\eta_0$ = $\sqrt{\mu_0 / \epsilon_0}$이다. 전자파 운동량의 방향은 파수 벡터의 방향이어야 하므로 식 (5)를 벡터적으로 표현하면 다음과 같다.

                         (6)

신기하게도 전자파 운동량 밀도(momentum density)는 포인팅 벡터(Poynting vector)와 밀접한 관계를 가진다. 또한 전자파의 복사 압력(electromagnetic radiation pressure) 정의 $\mathfrak{\bar f}$를 이용하면 다음 관계도 얻는다.

                       (7)

                       (8)

위 정의에서 켤레 복소수(complex conjugate)는 큰 의미없다. 켤레 복소수가 들어간 정의는 페이저(phasor)를 사용한다는 뜻이다. 식 (8)의 전자파 운동량 밀도를 이용해 전자파의 각운동량 밀도(angular momentum density)를 정할 수 있다.

                       (9)

아래 맥스웰 방정식을 식 (9)에 대입하면 다음을 얻는다.

                       (10: 패러데이의 법칙)

                       (11)

식 (11)에 다음 벡터 항등식(vector identity)을 적용해보자.

                         (A.1)

                         (A.2)

                (12)

식 (12)의 셋째 항을 계산하기 위해 다음 다이애드(dyad) 기반 벡터 항등식을 고려하자.

                         (13)

                       (14)

또한 우리가 계산하고 있는 양은 각운동량 밀도이므로 식 (14)는 다음 체적 적분과 관련되어 있다.

                       (15)

[그림 1] 자전과 공전 각운동량(출처: wikipedia.org)

식 (15)를 식 (12)에 대입하면 전자파의 각운동량 밀도를 다음 두 성분으로 나눌 수 있다.

                       (16)

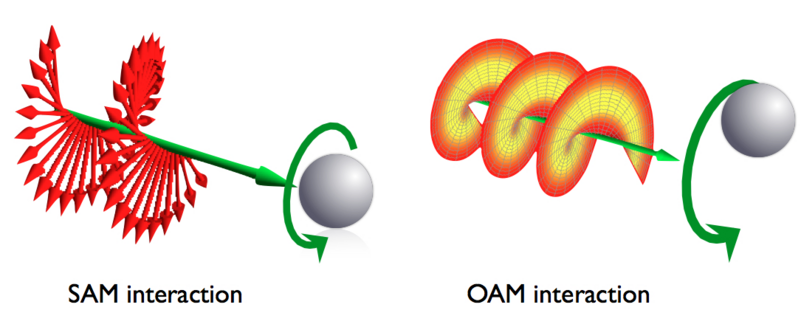
$\mathfrak{\bar J}_{\rm SAM}$은 선형 편파(Linear Polarization, LP) 경우 0이고 원형 편파(Circular Polarization, CP)는 값이 있으므로 자전 각운동량(Spin Angular Momentum, SAM)이라 부른다. 자전 각운동량은 원형 편파이므로 전자파 전달축 중심에서도 전기장과 자기장이 존재한다.[물론 원형 편파이므로 파면 전체에서 전자파 전력의 분포는 동일하다.] $\mathfrak{\bar J}_{\rm OAM}$은 축[$\bar r$]을 기준으로 계산하고 있으므로 공전 각운동량(Orbital Angular Momentum, OAM)이라 한다. 자전 각운동량과는 다르게 전자파 전달축 근방에서는 전자파 전력이 없고, 전달축에서 떨어진 특정한 반지름 위치의 전자파 전력이 최대가 된다.[전자파의 전력 분포 특성이 공전 궤도와 매우 유사하다.]

[그림 2] 정지한 하전 입자에 입사하는 균일 평면파

전자파의 운동량을 더 정확히 이해하기 위해 [그림 2]처럼 정지한 하전 입자에 작용하는 전자파 특성을 살펴보자. 초기 조건[$t = 0$]에서 정지[$v_x = v_z = 0$]해 있는 하전 입자에 균일 평면파(uniform plane wave)가 입사하면 전기장에 의해 하전 입자가 가속된다. $x$방향으로 가속된 하전 입자는 자기장에 의해서도 영향을 받는다. 매우 작은 시간인 $t = \Delta t$에서 변화된 $x$방향 속도와 자기력은 다음과 같다.

                       (17)

식 (17)을 이용해 운동 에너지와 $z$방향 운동량을 계산한다.

                       (18)

식 (18)에 제시한 결과는 식 (2)와 정확히 일치한다. 재미있는 결과지만 의문이 생긴다. 분명 전기장에 의해 $x$방향으로 가속이 되는데, 운동량 증가는 $z$방향으로 생긴다. 어떻게 해서 이런 현상이 생길까? 단순하게 보면 전자파는 식 (6)과 같은 운동량을 가지기 때문에, 전자파가 가진 운동량이 하전 입자에 전달되어 $z$방향 운동량이 생긴다고 설명할 수 있다. 이런 정성적인 설명을 바탕으로 로렌츠 힘(Lorentz force)을 이용해 좀더 정량적인 분석을 해보자.

                       (19)

식 (19)에 등장한 미분 방정식을 풀면 $x, z$방향 속도를 다음처럼 구할 수 있다.

                       (20)

사이클로트론(cyclotron) 동작 원리와 유사하게 $v_x$는 $+x, -x$방향을 진동하고 있다. 따라서 $x$방향 평균 운동량은 0이 되어, 전체 운동량에 기여하는 성분은 없다. 하지만 $z$방향 속도는 상수항이 있으므로, $z$방향 평균 운동량[$\langle p_z \rangle$]은 $mc$로 일정하다. 전기력과 평균 운동량과의 관계는 다음과 같다.

                       (21)

또한 식 (20)에서 $t \approx \Delta t$로 근사하면 식 (17)과 (18)을 얻을 수 있다.

이상의 논의에서 전자파 운동량은 식 (6)처럼 하전 입자에 직접 작용함을 볼 수 있다. 전자파에 전기장은 있지만, 전기장이 하전 입자에 전달하는 전기력은 상쇄되어 사라진다. 대신에 전자파 에너지가 전달되는 방향으로 하전 입자에 운동량이 전달된다.

[참고문헌]

[1] R. Fitzpatrick, Electromagnetic Energy and Momentum, Classical Electromagnetism, 2006.

[2] K. T. McDonald, "Orbital and spin angular momentum of electromagnetic fields," Physics Examples, 2009.

[3] R. N. C. Pfeifer, T. A. Nieminen, N. R. Heckenberg, and H. Rubinsztein-Dunlop, "Momentum of an electromagnetic wave in dielectric media," Rev. Mod. Phys., vol. 79, no. 4, pp. 1197–1216, Oct. 2007.

[다음 읽을거리]
1. 자기 단극자

르장드르의 미분 방정식(Legendre's Differential Equation)

[경고] 아래 글을 읽지 않고 "르장드르의 미분 방정식"을 보면 바보로 느껴질 수 있습니다.
1. 멱급수 기반 상미분 방정식 해법
2. 스튀름–리우빌 이론

식 (1)에 있는 르장드르의 미분 방정식(Legendre's differential equation)은 다소 복잡한 모양을 가지고 있다.

                        (1a)

                       (1b)

식 (1)에서 $x = \cos\theta$로 치환하면 조금은 단순해진 미분 방정식(differential equation)을 얻을 수 있다.

                       (2)

                        (3)

식 (2)를 식 (1)에 대입해서 정리하고 $1 - x^2$ = $\sin^2 \theta$ 및 $\frac{d}{d\theta}(\sin \theta \frac{dy}{d\theta})$ = $\cos \theta \frac{dy}{d\theta} + \sin \theta \frac{d^2 y}{d\theta^2}$를 이용하면, 식 (3)이 자연스럽게 유도된다. 식 (1), (3)에서 $m$ = $0$인 경우는 미분 방정식을 더욱 간략화할 수 있다.

                        (4a)

                       (4b)

                       (5)

식 (1)보다는 간편한 식 (4)의 해를 구한다. 점 $x$ = $0$은 미분 방정식 (4)의 정상점(ordinary point)이라서 다음과 같은 단순한 멱급수(power series) 전개가 가능하다.

                      (6)

식 (6)을 식 (4)에 전개해 항별로 정리하면 다음을 얻는다.

                      (7)

식 (7)이 $x$에 관계없이 $0$이기 위해서는 각 항이 모두 $0$이어야 한다. 따라서 르장드르 미분 방정식을 위한 다음 재귀 관계(recurrence relation)를 얻을 수 있다.

                      (8)

식 (8)의 분자를 인수 분해하면 다음과 같다.

                       (9)

식 (9)를 이용해 멱급수 해를 구하려면 $a_0, a_1$을 정해야 한다. 먼저 $a_0$ = $1$, $a_1$ = $0$이라 정하면 미분 방정식의 해는 다음처럼 표현되어야 한다.

                      (10a)

                      (10b)

반대로 $a_0$ = $0$, $a_1$ = $1$라 정하면 해는 다음처럼 다르게 표현된다.

          (11a)

                      (11b)

 식 (10)과 (11)을 이용하여 $m$ = $0$인 르장드르 미분 방정식의 일반해(general solution)는 다음처럼 쓸 수 있다.

                      (12)

특별히 차수(次數, degree) $n$이 정수인 경우는 르장드르 미분 방정식의 해가 무한 급수(infinite series)가 아니고 다항식(polynomial expression)이 될 수 있다. 차수 $n$이 짝수인 경우는 식 (10)이 다항식으로 표현되며, 차수 $n$이 홀수인 경우는 식 (11)이 다항식으로 된다. 이 경우의 해는 르장드르 다항식(Legendre polynomials) $P_n(x)$라 부른다[2]. 식 (10)과 (11)을 이용해 각 차수에 대한 르장드르 다항식을 써보면, 모든 차수 $n$에 대해 식 (13) 혹은 [표 1]처럼 유한 급수(finite series)로 표현할 수 있다.

                      (13)

[표 1] 르장드르 다항식의 유한 급수 표현식, $P_n(x)$

차수(degree), $n$	$P_n(x)$
0	$1$
1	$x$
2	$\displaystyle{\frac{1}{2}}(3x^2-1)$
3	$\displaystyle{\frac{1}{2}}(5x^3-3x)$
4	$\displaystyle{\frac{1}{8}}(35x^{4}-30x^{2}+3)$
5	$\displaystyle{\frac{1}{8}}(63x^{5}-70x^{3}+15x)$
6	$\displaystyle{\frac{1}{16}}(231x^{6}-315x^{4}+105x^{2}-5)$
7	$\displaystyle{\frac{1}{16}}(429x^{7}-693x^{5}+315x^{3}-35x)$
8	$\displaystyle{\frac{1}{128}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)$
9	$\displaystyle{\frac{1}{128}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)$
10	$\displaystyle{\frac{1}{256}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)$
11	$\displaystyle{\frac{1}{256}}(88179 x^{11} - 230945 x^9 + 218790 x^7 - 90090 x^5 + 15015 x^3 - 693 x)$

식 (13)에서 르장드르 다항식은 다음 성질을 만족하기 위해 식 (10)과 (11)의 상수를 조정하였다.

                      (14)

르장드르 다항식과는 다른 두번째 해에 해당하는 식은 다항식이 아니고 무한 급수이다. 이 무한 급수도 식 (10)과 (11)을 이용해 구한다. 예를 들어, $n$ = $0$인 경우는 식 (10)이 다항식을 만들고 식 (11)은 다음과 같은 무한 급수를 만든다.

                      (15)

식 (15)는 스튀름–리우빌 이론(Sturm–Liouville theory)으로 구할 수도 있다. 이 이론에 의해 두번째 해는 다음처럼 주어진다.

                       (16)

여기서 $\psi_1$은 미리 알고 있는 첫번째 해이며 $\psi_2$는 두번째 해이다. $\psi_1$ = $P_0(x)$ = $1$을 식 (16)에 대입해 적분한다.

                       (17)

르장드르 다항식 $P_n(x)$와는 다른 두번째 해는 무한 급수이며 보통 $Q_n(x)$로 표현한다. 비슷한 방법으로 $n$ = $1$을 구하면 다음과 같다.

                       (18)

식 (18)에서 상수 $a$는 별 의미없다. 정적분에서 시작점 $a$를 대입하면 원시 함수값은 결국 상수가 되므로, $Q_n(x)$를 표현할 때 과감하게 삭제할 수 있다.[$\because$ $a$와 관련된 적분 상수($c$)가 있더라도 결국 $cP_n(x)$가 되므로, 독립적인 두번째 해 $Q_n(x)$가 아닌 첫번째 해 $P_n(x)$에 속한다.] 차수 $n \ge 2$인 경우는 르장드르 미분 방정식의 재귀 관계(recurrence relation)를 이용해 구한다. $P_n(x)$와 $Q_n(x)$는 식 (4)의 르장드르 미분 방정식을 만족하므로 이 둘을 통칭하여 르장드르 함수(Legendre function)라 한다. 더 자세하게 보면 $P_n(x)$는 제1종 르장드르 함수(Legendre function of the first kind)이며 $Q_n(x)$는 제2종 르장드르 함수(Legendre function of the second kind)이다.

식 (10)이나 (11)과 같은 무한 급수(infinite series)를 다룰 때 조심해야 할 부분은 수렴 특성이다. 르장드르 함수는 식 (9)와 같은 깔끔한 재귀 관계가 있어 수렴성 해석은 매우 쉽다. 수열 $a_k$에서 $k+2$번째 항과 $k$번째 항의 비율을 다음처럼 계산한다.

                       (19)

첨수(index) $k$가 무한대로 갈 때 위와 같은 특성이 있다. 무한 등비 급수(infinite geometric series)와 식 (19)를 비교하면 르장드르 함수가 수렴하는 구간은 $|x| < 1$임을 알 수 있다. 물론 $n$이 정수인 경우는 식 (13)과 같은 르장드르 다항식을 만들 수 있기 때문에 수렴 구간은 무한대이다.

이상의 성질을 이용하면 $m \ne 0$ 경우인 식 (1)의 해를 구할 수 있다. 이를 위해 다음과 같은 변수 치환을 한다.

          (20)

식 (20)을 식 (1)에 대입해 정리하면 $u$에 대한 미분 방정식을 얻는다.

                  (21)

만약 $m$ = $0$이면, 식 (21)은 식 (4)가 된다. 미분 방정식 (21)의 의미를 알기 위해 식 (21)을 $x$에 대해 미분한다.

               (22)

신기하게도 한 번 미분하면 $m$이 1만큼 커진다. 이 성질에 의해 두 번 미분하면 $m$이 2만큼 커진다. 이 특성을 거꾸로 유추하면 식 (21)은 식 (4)를 $m$번 미분한 식이다. 따라서 식 (1)의 해는 다음처럼 쓸 수 있으며 버금 르장드르 함수(associated Legendre function)라 명한다.

                        (23)

여기서 $P_n^m(x)$는 제1종 버금 르장드르 함수(associated Legendre function of the first kind)이며 $Q_n^m(x)$는 제2종 버금 르장드르 함수(associated Legendre function of the second kind)이다. 식 (23)에 나오는 첨자 $n, m$은 각각 차수(次數, degree)와 계수(階數, order) 혹은 계층수(階層數)라 부른다. 여기서 계수는 미지수와 곱셈으로 연계되는 계수(係數, coefficient)와 한자가 완전 다르며 구별을 위해 계층수라고 명확히 부를 수도 있다.

[표 2] 버금 르장드르 함수의 유한 급수 표현식, $P_n^m(x)$

계층수(order), $m$	차수(degree), $n$	$P_n^m(x)$
1	1	$-\sqrt{1-x^2}$
1	2	$-3x\sqrt{1-x^2}$
2	2	$3(1-x^2)$
1	3	$\displaystyle{\frac{3}{2}}(1-5x^2)\sqrt{1-x^2}$
2	3	$15x(1-x^2)$
3	3	$-15\sqrt{(1-x^2)^3}$

[그림 1] 구면 조화 함수의 모양(출처: wikipedia.org)

식 (23)의 상수 $(-1)^m$은 없어도 되지만 버금 르장드르 함수를 이용해 정의하는 구면 조화 함수(球面 調和函數, spherical harmonics) 수식을 간편하게 만들기 위해 도입한 양이다. 상수 $(-1)^m$의 정식명은 콘던–쇼틀리 위상(Condon–Shortley phase)이다. 콘던–쇼틀리 위상을 생략한 경우는 다음처럼 버금 르장드르 함수를 표시한다.

                        (24)

식 (23)의 정의로 인해 $n, m$이 정수인 제1종 버금 르장드르 함수 $P_n^m(x)$는 다음 관계가 반드시 성립한다.

                       (25)

식 (26)에 제시한 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)을 이용하면, 식 (4)를 다음과 같은 스튀름–리우빌 형태(Sturm–Liouville form)로 쓸 수 있다.

                       (26)

                       (27)

따라서 르장드르 미분 방정식은 $p(x)$ = $1 - x^2$, $q(x)$ = $0$, $r(x)$ = $1$, $\lambda$ = $n(n+1)$인 스튀름–리우빌 미분 방정식이 된다. 식 (1)에 있는 다소 복잡한 르장드르 미분 방정식은 $p(x)$ = $1 - x^2$, $q(x)$ = $m^2/(1 - x^2)$, $r(x)$ = $1$, $\lambda$ = $n(n+1)$인 스튀름–리우빌 미분 방정식으로 간주한다. 왜냐하면 $x$ = $\pm 1$에서 발생하는 특이점을 처리하기 위해, 스튀름–리우빌 이론에서 특별한 제약이 없는 $q(x)$에 특이점이 있는 함수를 배정하기 때문이다. 어떤 경우에는 $p(x)$ = $1 - x^2$, $q(x)$ = $-n(n+1)$, $r(x)$ = $1/(1-x^2)$, $\lambda$ = $-m^2$라고 설정해서, $r(x)$가 $x$ = $\pm 1$에서 발산하도록 내버려둔다. 다만 $r(x)$는 발산하더라도 고유 함수 $\psi_m(x)$의 적분 $\int_{-1}^1 [\psi_m(x)]^2 r(x) \, dx$는 존재하도록 고유치 $\lambda$를 선택한다.

식 (1)로 표현한 미분 방정식에서 고유치 $\lambda$는 항상 $n(n+1)$이어야 할까? 아니다. 고유치는 경계 조건만 만족하면 어떤 값이든 가능하다. 하지만 르장드르 함수가 정의된 $[-1, 1]$에서 함수값을 유한하게 만들려면, 최소한 $\lambda$ = $n(n+1)$이 되어야 한다. 이 특성을 염두에 두고 식 (8)을 고유치 $\lambda$로 다시 쓴다.

                       (28)

지표(index) $k$가 매우 커질 때에 $a_{k+2} / a_k$는 1에 수렴해서, $x$ = $\pm 1$에서 $P_n(x)$는 발산하거나 정의되지 않는다.

                       (29)

점 $x$ = $\pm 1$의 발산 현상을 잡는 유일한 방법은 $\lambda$ = $n(n+1)$로 놓고 특정한 $k$에서 $k$ = $n$이 되어 $a_{k+2}$ = $0$이 되는 방식 뿐이다. 다만 $\lambda$ = $n(n+1)$인 조건을 잡더라도 $k$는 2칸씩 커지므로, $k$ = $n$이 될 수 없는 경우가 생긴다. 이때는 식 (15)처럼 $x$ = $\pm 1$에서 발산하는 $Q_n(x)$가 된다. 대신 $P_n(x)$는 유한 급수가 되어서 모든 점에서 잘 수렴한다.

[참고문헌]

[1] P. Lim, Series Solutions of Ordinary Differential Equations, Mathematical Methods in Physics I.

[2] A. M. Legendre, "Recherches sur l'attraction des spheroides homogenes (Research on the attraction of homogeneous spheroids)," Mémoires de Mathématique et de Physique (Memoirs of Mathematics and of Physics), pp. 411–434, 1785.

[다음 읽을거리]
1. 구 좌표계의 전자장 표현식

2. 르장드르 함수

3. 버금 르장드르 함수