[경고] 아래 글을 읽지 않고 "포물선의 방정식"을 보면 바보로 느껴질 수 있습니다.
포물선(抛物線, parabola)은 물건을 하늘로 던질 때 중력(gravity)과 속도(velocity)가 만드는 물체의 궤적이다. [그림 1]은 분수가 물을 하늘로 쏠 때 나타나는 포물선 형태를 보여준다.


[그림 1] 분수가 만드는 포물선(출처: wikipedia.org)
[그림 2] 포물선의 기하학적 정의(출처: wikipedia.org)
포물선은 기하학적으로 [그림 2]처럼 정의한다. 초점(focus) $\bar F$ = $(0, f)$에서 점 $\bar P_i$ = $(x_i, y_i)$까지 거리가 점 $\bar P_i$에서 준선(準線, directrix) $L$[$y$ = $-f$]까지 거리와 같은 점을 모두 모으면 포물선이 된다. 준선은 2차 곡선을 정의하거나 생성할 때 쓰이는 기준선이다. 이를 방정식으로 표현하면 다음과 같다.
 (1)
(1)
여기서 $(x, y)$는 포물선 위의 점이며 $f$[= $1/(4a)$]는 포물선의 초점, $(0, 0)$은 포물선의 꼭지점(vertex)이다. 포물선에서 꼭지점은 포물선의 끝에 해당하는 가장 높거나 낮은 점이며, 공식적으로는 포물선의 대칭축과 포물선의 교점으로 정의한다.

[그림 3] 원뿔로 만드는 포물선(출처: wikipedia.org)
[그림 3]에 소개한 초보적인 기하학을 이용해 포물선을 정의할 수 있다. 이 방법은 아폴로니우스Apollonius of Perga(대략 기원전 240–190)에 의해 제안되었다. 먼저 [그림 3]에서 원뿔(cone)의 꼭지점을 $A$라 한다. 다음에 원뿔을 잘라 두 개의 원[짙은 파란색]을 만든다. 첫번째 원은 선분 $\overline{PK}$를 지름($2r$)으로 가진다. 두번째 원은 선분 $\overline{BC}$가 지름이다. 원뿔 바깥선과 평행하게 선분 $\overline{PM}$ = $y$을 그어 선분 $\overline{MC}$ = $2r$이 되게 한다. 선분 $\overline{PM}$은 원뿔 바깥선과 평행이므로 $\angle PBM$ = $\angle PMB$가 성립하여 $\triangle PBM$은 이등변 삼각형이 된다. 선분 $\overline{PM}$이 원뿔 기준선[점 $A$에서 두번째 원에 내린 수직선]과 이루는 각도를 $\theta$라 하면 $\overline{BM}$ = $2 y \sin \theta$가 된다. 또한 선분 $\overline{DE}$ = $2x$는 반지름이 $r$인 원에 접하므로 이 원에 수직이며, 탈레스의 정리(Thales' theorem)에 의해 $\angle BEC$도 수직이다. 따라서 다음이 성립한다.
 (2)
(2)
식 (1)을 고려하면 포물선의 초점은 $f$ = $r \sin \theta$가 된다.


[그림 4] 새로운 준선을 가진 포물선(출처: wikipedia.org)
관점을 좀 바꾸어보면 [그림 2]의 준선은 [그림 4]처럼 바꿀 수 있다. [그림 4]의 준선 $M$은 초점 $\bar F$ = $(0, f)$의 아래가 아닌 초점 위에 있다. 예를 들어, 준선 $M$이 $y$ = $g$[$g > 0$]에 있다고 가정한다. 그러면 [그림 2]와 [그림 4]에 있는 준선 $L$과 $M$ 간의 거리는 항상 $\overline{Q_i P_i} + \overline{P_i R_i}$ = $|g - (-f)|$ = $|f + g|$가 된다. [그림 2]의 결과에 의해 $\overline{Q_i P_i}$ = $\overline{F P_i}$이기도 하다. 따라서 [그림 4]의 경우에도 초점에서 준선까지 가는 거리는 항상 일정하므로, 식 (1)과 같은 포물선의 방정식을 다음처럼 얻을 수도 있다.
 (3)
(3)
여기서 $f > 0$, $y < g$이다. 준선이 양의 $y$축에 있더라도 포물선의 방정식은 식 (1)과 동일하게 얻어진다. 또한 $g$가 0보다 크기만 하면, $g$에 관계없이 초점과 준선 사이의 거리는 항상 동일하다. 별것 아닌 [그림 4]의 개념이 현존하는 반사기 안테나(reflector antenna) 혹은 조명 기구의 기본적인 원리이다.
[그림 5] 포물형 반사판 안테나(출처: wikimedia.org)
[그림 6] 태양열 조리기(출처: wikipedia.org)
[그림 7] 자동차의 전조등(출처: wikipedia.org)
[그림 5–7]은 포물선의 원리를 적용한 여러 제품을 보여준다. [그림 5]는 포물형 반사판 안테나(parabolic reflector antenna)이다. 급전부(feed)는 포물선의 초점에 있다. 급전부에서 나온 전자파는 포물형 금속 반사판에서 반사되어 준선 방향에 수직인 방향으로 전달된다. 이 방식은 고이득 안테나(high-gain antenna, HGA)를 만드는 일반 원리가 된다. [그림 6]은 태양열 조리기(solar cooker)의 예를 보여준다. 태양빛이 포물형 반사경에서 반사되어 초점에 집속된다. 초점에 조리기를 두면 태양열이 강하게 집속되어 요리가 가능하다. [그림 7]은 자동차의 전조등(headlight)이다. 초점 위치에 광원을 두고 포물형 반사경에 쏘면 대부분의 빛이 전방으로 강하게 전달된다.
[그림 8] 포물선의 반사 원리(출처: wikipedia.org)
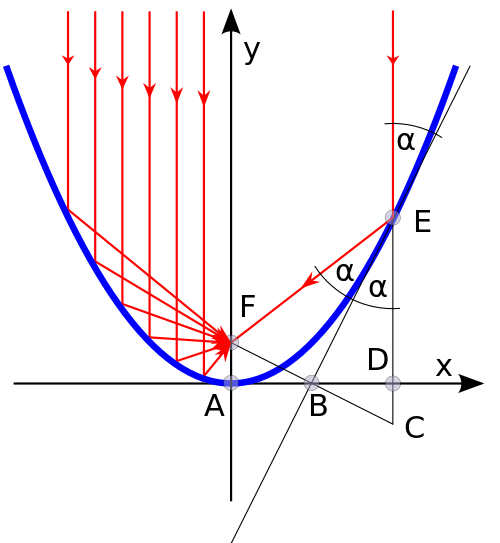
그러면 [그림 5–7]의 동작 원리를 간단한 포물선 개념으로 설명한다. 이를 위해 [그림 8]에 제시한 포물면의 반사 특성을 계산해야 한다. 준선에 수직인 방향으로 광선(ray)이 들어온다고 생각한다. 이 광선과 포물면이 이루는 각도는 $\alpha$이다. 또한 [그림 2]와 같이 음의 $y$축에 있는 준선 위의 점을 $C$라 한다. 그러면 포물선의 정의에 의해 삼각형 $\triangle ECF$는 이등변 삼각형이다.[∵ 초점에서 포물선 점 $(x, y)$의 거리와 포물선 점 $(x, y)$과 준선까지 거리는 항상 같다.] 선분 $\overline{CF}$와 $\overline{EB}$가 수직임을 증명하기 위해 식 (1)에 있는 포물선의 방정식을 이용한다.
 (4)
(4)
 (4)
(4)
여기서 $\bar T$는 접선의 기울기이다. 삼각형 $\triangle ECF$는 이등변 삼각형이면서 선분 $\overline{EB}$는 선분 $\overline{CF}$에 수직하므로 $\angle FEB$ = $\angle CEB$가 된다. 즉, 준선에 수직인 방향으로 들어온 광선은 입사각과 동일한 각도로 반사되어 초점으로 들어간다. 이런 성질은 빛에 대한 금속면 반사 법칙과 동일하다. 그래서 포물형 반사기에 반사된 빛은 초점에 모두 모인다.

(a) 꼭지점 기준 좌표계[꼭지점이 원점]

(b) 모서리 기준 좌표계[모서리가 $y$ = $0$]
[그림 9] 유한한 포물선의 모양
포물선이 복잡하기는 하지만 [그림 9]의 $D, d$를 알면 쉽게 포물선 상수 $a$ 혹은 초점 $f$를 결정할 수 있다.
 (5)
(5)
식 (5)는 지름 $D$, 깊이 $d$를 가진 유한한 포물선을 측정하여 포물선 상수 $a$와 초점 $f$를 결정하기 위한 가장 쉬운 방법이다. 예를 들어, [그림 9(a)]와 같은 포물선은 다음 식처럼 표현된다.
 (6)
(6)여기서 좌표계는 포물선의 꼭지점으로 설정한다. 식 (6)으로부터 $x$ = $D/2$이면 당연히 $y$ = $d$가 나온다. 만약 포물선이 놓여있는 지름 위치[$x$의 범위 = $(-D/2, D/2)$]가 [그림 9(b)]처럼 $y$ = $0$이 된다면 포물선의 방정식은 모서리 기준 좌표계[포물선의 모서리를 $y$ = $0$으로 선택, 꼭지점은 $(0, -d)$에 위치]에서 기술된다.
 (7a)
(7a) (7b)
(7b)
식 (7)에서 $x$ = $\pm D/2$이면 $y$ = $0$이 된다.
포물선의 표현에 사용한 식 (1)은 2차 곡선을 정의하거나 분류할 때 사용하는 이심률(離心率, eccentricity)의 정의이다. 식 (1)과 동일하게, 초점 $\bar F$에서 2차 곡선 위의 점 $\bar P$까지 거리와 준선(準線, directrix)에서 $\bar P$까지 거리의 비율을 이용해 이심률을 다음처럼 정의한다.
 (8)
(8)

[그림 10]처럼 포물선이 회전한 경우는 포물선의 방정식이 식 (1)처럼 간단히 표현되지 않는다. [그림 10]의 기하 구조에 대해, 식 (1)과 같은 논리로 거리를 계산한다.
포물선의 표현에 사용한 식 (1)은 2차 곡선을 정의하거나 분류할 때 사용하는 이심률(離心率, eccentricity)의 정의이다. 식 (1)과 동일하게, 초점 $\bar F$에서 2차 곡선 위의 점 $\bar P$까지 거리와 준선(準線, directrix)에서 $\bar P$까지 거리의 비율을 이용해 이심률을 다음처럼 정의한다.
 (8)
(8)
여기서 $L$은 준선에서 $\bar P$까지 거리이다. 식 (8)에 의해 포물선의 이심률은 1이다.

[그림 10] 회전한 포물선(출처: wikipedia.org)
 (9)
(9)여기서 포물선 위의 점은 $(x, y)$, 초점은 $\bar F$ = $(f_x, f_y)$, 준선은 $ax+by+c$ = $0$, 준선과 포물선의 거리는 점과 직선 사이의 거리를 사용, 나머지 항을 담아놓은 함수는 직선처럼 $F(x, y)$ = $Ax + By + C$로 선택한다. 식 (9)에서 유추하여 포물선이 될 수 있는 임의의 2차 곡선은 다음 형태를 가진다.
 (10)
(10)여기서 $D$는 원뿔 곡선의 판별식(discriminant of conic section)이다. 신기하게도 원뿔 곡선의 판별식은 2차 방정식의 판별식과 부호만 다르고 완전 동일하다. 만약 판별식이 $D$ = $0$으로 나오면, 이 2차 곡선은 [그림 10]과 같은 회전한 포물선이 된다.

[그림 11] 초점 기준 좌표계
 (11a)
(11a)여기서 $x$ = $\rho \sin \psi$, $y$ = $-\rho \cos \psi$이다. 만약 준선을 $y$ = $0$에 두면, 포물선 위의 임의 점으로 선을 그리더라도 그 길이는 항상 $2f$가 된다. 따라서 [그림 11]을 바탕으로 극 좌표계(polar coordinate system) $(\rho, \psi)$로 식 (11a)를 다시 표현한다.
 (11b)
(11b)
여기서 $\rho_0$ = $\sqrt{(D/2)^2 + (f-d)^2}$, $\psi_0$ = $\tan^{-1} [D \mathbin{/} [2(f-d)]]$이다. 다시 한 번 포물선의 모서리에 대해 $2f$ = $\rho_0 + f - d$를 적용해서 포물선의 나팔각(flare angle) $\psi_0$을 간편하게 공식화한다.
 (12)
(12)


.jpg/640px-Headlight_(2966062110).jpg)
감사합니다!!!!
답글삭제감사까지야 -.-;; 고등학교 수준 정도의 내용을 정리한 것 뿐입니다. ^^
삭제그림4의 L을 준선이라고 불러도 되는 건가요? 포물선은 준선과 점 사이의 거리와 초점과 점 사이의 거리가 같은 점들의 집합이라고 알고 있는데... 잘 몰라서 질문드립니다
답글삭제가능해요, 최지민님. ^^
삭제포물선의 반사의 원리에서 P = OF-OC = CF로 되지않나요?? 궁금해서 질문 드립니다!
답글삭제[그림 8]을 말씀하시는 거죠? 포물선 성질에 의해 선분 EF와 EC가 같아요.
삭제앗... 답변 감사합니다.
삭제넵! [그림 8] 아래의 식(4)에서 벡터 FC의 계산에서 (벡터) AF - AC = (-x , 2f) = (벡터) CF 이니까 벡터FC가 아니라 벡터CF가 되야되지않나요??
다시 질문드려서 죄송합니다...
Unknown님, 지적 정말 감사합니다. 으TL 착각해서 틀렸었네요. 방금 고쳤어요.
삭제넵! 답변감사드립니다!
삭제