1. 멱급수 기반 상미분 방정식 해법
2. 스튀름–리우빌 이론
식 (1)에 있는 르장드르의 미분 방정식(Legendre's differential equation)은 다소 복잡한 모양을 가지고 있다.
(1a)
(1b)
식 (1)에서 $x = \cos\theta$로 치환하면 조금은 단순해진 미분 방정식(differential equation)을 얻을 수 있다.
(2)
(3)식 (2)를 식 (1)에 대입해서 정리하고 $1 - x^2$ = $\sin^2 \theta$ 및 $\frac{d}{d\theta}(\sin \theta \frac{dy}{d\theta})$ = $\cos \theta \frac{dy}{d\theta} + \sin \theta \frac{d^2 y}{d\theta^2}$를 이용하면, 식 (3)이 자연스럽게 유도된다. 식 (1), (3)에서 $m$ = $0$인 경우는 미분 방정식을 더욱 간략화할 수 있다.
(4a)
(4b)
(5)
식 (1)보다는 간편한 식 (4)의 해를 구한다. 점 $x$ = $0$은 미분 방정식 (4)의 정상점(ordinary point)이라서 다음과 같은 단순한 멱급수(power series) 전개가 가능하다.
(6)
식 (6)을 식 (4)에 전개해 항별로 정리하면 다음을 얻는다.
(7)
식 (7)이 $x$에 관계없이 $0$이기 위해서는 각 항이 모두 $0$이어야 한다. 따라서 르장드르 미분 방정식을 위한 다음 재귀 관계(recurrence relation)를 얻을 수 있다.
(8)
식 (8)의 분자를 인수 분해하면 다음과 같다.
(9)
식 (9)를 이용해 멱급수 해를 구하려면 $a_0, a_1$을 정해야 한다. 먼저 $a_0$ = $1$, $a_1$ = $0$이라 정하면 미분 방정식의 해는 다음처럼 표현되어야 한다.
(10a)
(10b)
반대로 $a_0$ = $0$, $a_1$ = $1$라 정하면 해는 다음처럼 다르게 표현된다.
(11a)
(11b) 식 (10)과 (11)을 이용하여 $m$ = $0$인 르장드르 미분 방정식의 일반해(general solution)는 다음처럼 쓸 수 있다.
(12)
특별히 차수(次數, degree) $n$이 정수인 경우는 르장드르 미분 방정식의 해가 무한 급수(infinite series)가 아니고 다항식(polynomial expression)이 될 수 있다. 차수 $n$이 짝수인 경우는 식 (10)이 다항식으로 표현되며, 차수 $n$이 홀수인 경우는 식 (11)이 다항식으로 된다. 이 경우의 해는 르장드르 다항식(Legendre polynomials) $P_n(x)$라 부른다[2]. 식 (10)과 (11)을 이용해 각 차수에 대한 르장드르 다항식을 써보면, 모든 차수 $n$에 대해 식 (13) 혹은 [표 1]처럼 유한 급수(finite series)로 표현할 수 있다.
(13)[표 1] 르장드르 다항식의 유한 급수 표현식, $P_n(x)$
| 차수(degree), $n$ | $P_n(x)$ |
|---|---|
| 0 | $1$ |
| 1 | $x$ |
| 2 | $\displaystyle{\frac{1}{2}}(3x^2-1)$ |
| 3 | $\displaystyle{\frac{1}{2}}(5x^3-3x)$ |
| 4 | $\displaystyle{\frac{1}{8}}(35x^{4}-30x^{2}+3)$ |
| 5 | $\displaystyle{\frac{1}{8}}(63x^{5}-70x^{3}+15x)$ |
| 6 | $\displaystyle{\frac{1}{16}}(231x^{6}-315x^{4}+105x^{2}-5)$ |
| 7 | $\displaystyle{\frac{1}{16}}(429x^{7}-693x^{5}+315x^{3}-35x)$ |
| 8 | $\displaystyle{\frac{1}{128}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)$ |
| 9 | $\displaystyle{\frac{1}{128}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)$ |
| 10 | $\displaystyle{\frac{1}{256}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)$ |
| 11 | $\displaystyle{\frac{1}{256}}(88179 x^{11} - 230945 x^9 + 218790 x^7 - 90090 x^5 + 15015 x^3 - 693 x)$ |
식 (13)에서 르장드르 다항식은 다음 성질을 만족하기 위해 식 (10)과 (11)의 상수를 조정하였다.
(14)
르장드르 다항식과는 다른 두번째 해에 해당하는 식은 다항식이 아니고 무한 급수이다. 이 무한 급수도 식 (10)과 (11)을 이용해 구한다. 예를 들어, $n$ = $0$인 경우는 식 (10)이 다항식을 만들고 식 (11)은 다음과 같은 무한 급수를 만든다.
(15)
식 (15)는 스튀름–리우빌 이론(Sturm–Liouville theory)으로 구할 수도 있다. 이 이론에 의해 두번째 해는 다음처럼 주어진다.
(16)
여기서 $\psi_1$은 미리 알고 있는 첫번째 해이며 $\psi_2$는 두번째 해이다. $\psi_1$ = $P_0(x)$ = $1$을 식 (16)에 대입해 적분한다.
(17)
르장드르 다항식 $P_n(x)$와는 다른 두번째 해는 무한 급수이며 보통 $Q_n(x)$로 표현한다. 비슷한 방법으로 $n$ = $1$을 구하면 다음과 같다.
(18)
식 (18)에서 상수 $a$는 별 의미없다. 정적분에서 시작점 $a$를 대입하면 원시 함수값은 결국 상수가 되므로, $Q_n(x)$를 표현할 때 과감하게 삭제할 수 있다.[$\because$ $a$와 관련된 적분 상수($c$)가 있더라도 결국 $cP_n(x)$가 되므로, 독립적인 두번째 해 $Q_n(x)$가 아닌 첫번째 해 $P_n(x)$에 속한다.] 차수 $n \ge 2$인 경우는 르장드르 미분 방정식의 재귀 관계(recurrence relation)를 이용해 구한다. $P_n(x)$와 $Q_n(x)$는 식 (4)의 르장드르 미분 방정식을 만족하므로 이 둘을 통칭하여 르장드르 함수(Legendre function)라 한다. 더 자세하게 보면 $P_n(x)$는 제1종 르장드르 함수(Legendre function of the first kind)이며 $Q_n(x)$는 제2종 르장드르 함수(Legendre function of the second kind)이다.
식 (10)이나 (11)과 같은 무한 급수(infinite series)를 다룰 때 조심해야 할 부분은 수렴 특성이다. 르장드르 함수는 식 (9)와 같은 깔끔한 재귀 관계가 있어 수렴성 해석은 매우 쉽다. 수열 $a_k$에서 $k+2$번째 항과 $k$번째 항의 비율을 다음처럼 계산한다.
(19)
첨수(index) $k$가 무한대로 갈 때 위와 같은 특성이 있다. 무한 등비 급수(infinite geometric series)와 식 (19)를 비교하면 르장드르 함수가 수렴하는 구간은 $|x| < 1$임을 알 수 있다. 물론 $n$이 정수인 경우는 식 (13)과 같은 르장드르 다항식을 만들 수 있기 때문에 수렴 구간은 무한대이다.
이상의 성질을 이용하면 $m \ne 0$ 경우인 식 (1)의 해를 구할 수 있다. 이를 위해 다음과 같은 변수 치환을 한다.
(20)
식 (20)을 식 (1)에 대입해 정리하면 $u$에 대한 미분 방정식을 얻는다.
(21)만약 $m$ = $0$이면, 식 (21)은 식 (4)가 된다. 미분 방정식 (21)의 의미를 알기 위해 식 (21)을 $x$에 대해 미분한다.
(22)
신기하게도 한 번 미분하면 $m$이 1만큼 커진다. 이 성질에 의해 두 번 미분하면 $m$이 2만큼 커진다. 이 특성을 거꾸로 유추하면 식 (21)은 식 (4)를 $m$번 미분한 식이다. 따라서 식 (1)의 해는 다음처럼 쓸 수 있으며 버금 르장드르 함수(associated Legendre function)라 명한다.
(23)
여기서 $P_n^m(x)$는 제1종 버금 르장드르 함수(associated Legendre function of the first kind)이며 $Q_n^m(x)$는 제2종 버금 르장드르 함수(associated Legendre function of the second kind)이다. 식 (23)에 나오는 첨자 $n, m$은 각각 차수(次數, degree)와 계수(階數, order) 혹은 계층수(階層數)라 부른다. 여기서 계수는 미지수와 곱셈으로 연계되는 계수(係數, coefficient)와 한자가 완전 다르며 구별을 위해 계층수라고 명확히 부를 수도 있다.
[표 2] 버금 르장드르 함수의 유한 급수 표현식, $P_n^m(x)$
| 계층수(order), $m$ | 차수(degree), $n$ | $P_n^m(x)$ |
|---|---|---|
| 1 | 1 | $-\sqrt{1-x^2}$ |
| 1 | 2 | $-3x\sqrt{1-x^2}$ |
| 2 | 2 | $3(1-x^2)$ |
| 1 | 3 | $\displaystyle{\frac{3}{2}}(1-5x^2)\sqrt{1-x^2}$ |
| 2 | 3 | $15x(1-x^2)$ |
| 3 | 3 | $-15\sqrt{(1-x^2)^3}$ |
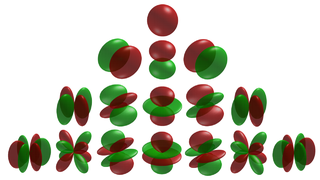
[그림 1] 구면 조화 함수의 모양(출처: wikipedia.org)
식 (23)의 상수 $(-1)^m$은 없어도 되지만 버금 르장드르 함수를 이용해 정의하는 구면 조화 함수(球面 調和函數, spherical harmonics) 수식을 간편하게 만들기 위해 도입한 양이다. 상수 $(-1)^m$의 정식명은 콘던–쇼틀리 위상(Condon–Shortley phase)이다. 콘던–쇼틀리 위상을 생략한 경우는 다음처럼 버금 르장드르 함수를 표시한다.
(24)
식 (23)의 정의로 인해 $n, m$이 정수인 제1종 버금 르장드르 함수 $P_n^m(x)$는 다음 관계가 반드시 성립한다.
(25)
식 (26)에 제시한 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)을 이용하면, 식 (4)를 다음과 같은 스튀름–리우빌 형태(Sturm–Liouville form)로 쓸 수 있다.
(26)
(27)
따라서 르장드르 미분 방정식은 $p(x)$ = $1 - x^2$, $q(x)$ = $0$, $r(x)$ = $1$, $\lambda$ = $n(n+1)$인 스튀름–리우빌 미분 방정식이 된다. 식 (1)에 있는 다소 복잡한 르장드르 미분 방정식은 $p(x)$ = $1 - x^2$, $q(x)$ = $m^2/(1 - x^2)$, $r(x)$ = $1$, $\lambda$ = $n(n+1)$인 스튀름–리우빌 미분 방정식으로 간주한다. 왜냐하면 $x$ = $\pm 1$에서 발생하는 특이점을 처리하기 위해, 스튀름–리우빌 이론에서 특별한 제약이 없는 $q(x)$에 특이점이 있는 함수를 배정하기 때문이다. 어떤 경우에는 $p(x)$ = $1 - x^2$, $q(x)$ = $-n(n+1)$, $r(x)$ = $1/(1-x^2)$, $\lambda$ = $-m^2$라고 설정해서, $r(x)$가 $x$ = $\pm 1$에서 발산하도록 내버려둔다. 다만 $r(x)$는 발산하더라도 고유 함수 $\psi_m(x)$의 적분 $\int_{-1}^1 [\psi_m(x)]^2 r(x) \, dx$는 존재하도록 고유치 $\lambda$를 선택한다.
식 (1)로 표현한 미분 방정식에서 고유치 $\lambda$는 항상 $n(n+1)$이어야 할까? 아니다. 고유치는 경계 조건만 만족하면 어떤 값이든 가능하다. 하지만 르장드르 함수가 정의된 $[-1, 1]$에서 함수값을 유한하게 만들려면, 최소한 $\lambda$ = $n(n+1)$이 되어야 한다. 이 특성을 염두에 두고 식 (8)을 고유치 $\lambda$로 다시 쓴다.
(28)지표(index) $k$가 매우 커질 때에 $a_{k+2} / a_k$는 1에 수렴해서, $x$ = $\pm 1$에서 $P_n(x)$는 발산하거나 정의되지 않는다.
(29)점 $x$ = $\pm 1$의 발산 현상을 잡는 유일한 방법은 $\lambda$ = $n(n+1)$로 놓고 특정한 $k$에서 $k$ = $n$이 되어 $a_{k+2}$ = $0$이 되는 방식 뿐이다. 다만 $\lambda$ = $n(n+1)$인 조건을 잡더라도 $k$는 2칸씩 커지므로, $k$ = $n$이 될 수 없는 경우가 생긴다. 이때는 식 (15)처럼 $x$ = $\pm 1$에서 발산하는 $Q_n(x)$가 된다. 대신 $P_n(x)$는 유한 급수가 되어서 모든 점에서 잘 수렴한다.
[참고문헌]
[다음 읽을거리]
1. 구 좌표계의 전자장 표현식
[2] A. M. Legendre, "Recherches sur l'attraction des spheroides homogenes (Research on the attraction of homogeneous spheroids)," Mémoires de Mathématique et de Physique (Memoirs of Mathematics and of Physics), pp. 411–434, 1785.
[다음 읽을거리]
1. 구 좌표계의 전자장 표현식
(1b)
(1c)
(2)
(3)
(6)
(7)
(8)
(10a)
(1.1)
(1.2a)
(1.2b)
(1.4)
(1.5)
(1.6)
(2.1)
(2.2)
(2.3)
(2.5a)
(2.5b)
(2.6)
(2.7)
(3.1)
(3.5)
(4.1)
(4.2)
(4.4)
(5.1)