1. 텐서와 좌표 변환
2. 텐서 미적분학
3. 직교 좌표계 텐서 미적분학
4. 텐서를 이용한 맥스웰 방정식
텐서 이론(tensor theory)이 필요한 전자기학 분야가 최근에 각광을 받고 있다[1]–[3]. 공학자 입장에서는 수학적 놀이에 불과한 텐서가 새로운 전자기학적 물질을 개발할 수 있는 유용한 도구가 되었다. 아래 동영상은 새로운 물질로 만든 투명 망토(invisibility cloak)가 전자파를 통과시키는 모습을 가시적으로 보여준다.
[투명 망토(invisibility cloak)의 원리]
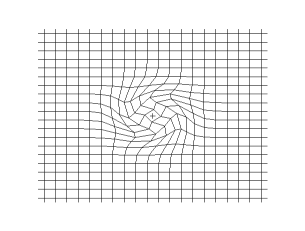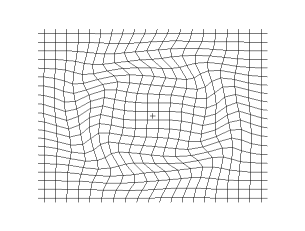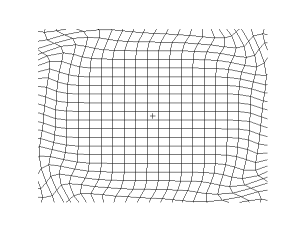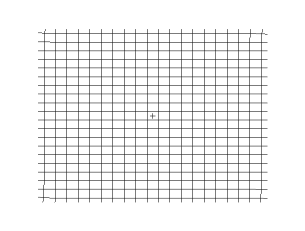
[그림 1]과 같은 텐서 이론에 기반을 둔 변환 전자기학 기법[3] 자체는 사실 새로운 내용이 없다. 이미 맥스웰 방정식의 좌표 불변성은 1962년아인슈타인 사후 7년, 국가재건최고회의 시절에 책[4]으로도 소개가 되었다. 그러면 뭐가 새롭다는 뜻인가? 데카르트 좌표계(Cartesian coordinate system)와 유사한 형태로 맥스웰 방정식(Maxwell's equations)을 모든 임의의 일반 좌표계에서 표현할 수 있다는 개념이 새로운 관점이다[5]–[7]. 이를 이용하면 위의 투명 망토와 같은 물질을 설계할 수 있는 유전율값과 투자율값을 찾을 수 있다. 이 말은 바로 이해되지는 않지만, 아래 유도를 보면 쉽게 파악할 수 있다.
[그림 1] 데카르트 좌표계와 일반 좌표계 간의 좌표 변환(출처: wikipedia.org)
맥스웰 방정식을 텐서로 표현했기 때문에 맥스웰 방정식이 좌표 불변성을 가짐은 자명하다.
(1: 패러데이의 법칙)
(2: 암페어의 법칙)
(3: 쿨롱의 법칙)
(4: 비오–사바르 법칙)
여기서 $\mathcal{G}$는 계량 텐서의 행렬식, $\varepsilon_{ijk}$는 레비-치비타 기호(Levi-Civita symbol)이다. 그러면 맥스웰 방정식이 좌표 불변성을 가질 때 맥스웰 방정식이 가진 특성을 찾아보자. 이를 위해 일반 좌표계 $U$에서 또 다른 일반 좌표계 $V$로 가는 좌표 변환이 가진 텐서 관계식을 유도하자.
(5: 공변 벡터)
(6: 반변 벡터)
(7)
(8)
(9)
여기서 $(\cdot)'$는 일반 좌표계 $V$의 매개변수, $J^{ji}_{v,u}$는 야코비 행렬(Jacobian matrix), $g_{ij}$는 계량 텐서(metric tensor), $\mathcal{J}_{v,u}$는 야코비 행렬식(Jacobian or Jacobian determinant)이다. 위의 식 (8)과 (9) 유도에는 텐서 좌표 변환, 텐서 미적분학 개념이 필요하다. 식 (8)과 (9)를 식 (1)에 대입하면 패러데이 법칙은 아래 관계식을 만족한다.
(10)
여기서 야코비 행렬과 레비-치비타 기호의 관계식을 아래와 같이 이용하였다.
(11)
식 (11)이 성립함은 자명하다. 식 (11)의 첫째 줄에서 $i$와 $j$는 교환하더라도 그 값은 동일하다. 하지만, 식 (11)의 둘째 줄에서 $i$와 $j$를 교환하면 레비-치비타 기호에 의해 $\varepsilon_{ijk} = -\varepsilon_{jik}$가 되므로 동일한 두 항이 서로 상쇄되어 전체적으로 0이 된다. 식 (10)에 텐서 $J^{k'k}_{v,u}$를 양변에 곱하고 정리해보자.
(12)
(13)
(14)
그러면 일반 좌표계 $U$의 전자기장과 일반 좌표계 $V$의 전자기장 사이 관계는 아래와 같이 정의할 수 있다.
(15)
또한, 식 (15)의 전자기장 벡터는 식 (5)의 공변 벡터(covariant vector)를 이용해 표현하였다.
식 (12)의 방법론을 식 (2)에 적용하면 다음을 얻을 수 있다.
(16)
(17)
식 (15)와 (17)에 정의된 좌표 변환을 이용하면 식 (1)과 (2)는 자동으로 만족된다. 하지만, 식 (3)과 (4)도 동시에 만족해야 좌표 변환 (15)와 (17)이 제대로 정의된다. 식 (15)와 (17)을 식 (3)에 대입해서 정리해보자.
(18)
식 (18)의 증명은 다소 난해하다. 증명을 위해서는 먼저 야코비 행렬과 행렬식의 관계식을 유도해야한다.
(19)
여기서 ${\rm cof}(\cdot)$는 행렬의 여인자(cofactor)이다. 행렬식과 여인자의 관계는 행(行, row)에 대한 라플라스 전개(Laplace expansion)를 이용해 다음으로 표현할 수 있다.
(20)
여기서 $C_{ij}$는 행렬 $\bf A$의 여인자(餘因子, cofactor), $M_{ij}$는 원소 $a_{ij}$의 소행렬식(小行列式, minor)이다. 예를 들어 소행렬식 $M_{23}$은 아래와 같이 계산할 수 있다.
(21)
즉, $M_{23}$은 2행과 3열 원소 전체를 식 (21)처럼 삭제한 후 계산하는 행렬식이다. 또한, 식 (9)의 셋째 줄 증명처럼 $J_{u,v}$와 $J_{v,u}$는 서로 역행렬(inverse matrix) 관계이므로 아래가 성립한다.
(22)
식 (22)를 대입하고 식 (11)을 이용하면 식 (19)를 증명할 수 있다. 식 (18)과 동일한 방법을 사용하면 식 (4)의 좌표 변환 특성이 아래와 같이 얻어진다.
(23)
전류(electric current)와 자류(magnetic current)에 대한 연속 방정식도 동일한 방법으로 증명할 수 있다. 예를 들면 식 (24)에 있는 전류의 연속 방정식(continuity equation)에 식 (17)과 (18)의 결과를 대입하면 연속 방정식의 좌표 불변성이 증명된다.
(24)
(25)
이상에서 유도한 전자기장과 원천의 좌표 변환 관계를 행렬로 표현하면 아래와 같다.
(26)
(27)
여기서 ${\bf J}_{v,u}$는 식 (28)과 같은 야코비 행렬이며 전자기장과 전류 및 자류 밀도는 식 (29)와 같이 반변 벡터로 표현하였다.
(28)
(29)
식 (26)과 (27)에서는 일반 좌표계 $U$에서 전자기장 문제를 풀면 식 (26)의 좌표 변환에 의해 일반 좌표계 $V$의 문제도 자동적으로 풀리는 특성이 중요하다. 또한, 유전율(permittivity)과 투자율(permeability)도 좌표 변환에 의해 바뀌게 된다. 식 (30)과 같이 유전율이나 투자율이 등방 매질(等方媒質, isotropic media: 방향에 관계없이 매질 특성이 일정)이면 좌표 변환 여부에 관계없이 유전율이나 투자율은 바뀌지 않는다.
(30)
참고문헌 [3], [6], [7]에 주어진 변환 전자기학을 위한 좌표 변환 공식을 얻으려면 머리를 좀 써야 한다. 여기까지 따라왔으면 어려운 점은 거의 없다. 먼저 데카르트 좌표계의 벡터 특성을 살펴보자.
(31)
(32)
데카르트 좌표계에서는 계량 텐서가 크로네커 델타(Kronecker delta)이기 때문에 식 (32)의 $h_1 = h_2 = h_3 = 1$이 된다. 즉, 공변 벡터(covariant vector)와 반변 벡터(contravariant vector)는 단위 벡터(unit vector)이며 서로 같게 된다. 따라서, 일반적인 맥스웰 방정식인 식 (1)에서 (4)를 데카르트 좌표계에서는 반변 벡터로만 표현할 수 있게 된다. 예를 들어 식 (1)은 다음으로 표현된다.
(33)
식 (1)과 (33)의 차이점은 공변 벡터와 반변 벡터의 사용에 있다. 식 (1)은 공변/반변 벡터가 섞여있지만 식 (33)은 반변 벡터로만 표현되었다. 식 (12) 유도와 동일한 방법으로 데카르트 좌표계 $X$에서 일반 좌표계 $U$로 갈 때 식 (33)이 변하는 특성을 찾아보자.
(34)
식 (34)에 $J^{k'k}_{u,x}$를 곱해 정리하면 다음을 얻는다.
(35)
다음 관계식을 이용하여 식 (35)를 치환하였다.
(36)
좌표 변환을 하더라도 식 (33)과 (35)가 서로 유사한 모양을 가짐은 재미있다. 즉, 좌표 변환된 식 (35)도 데카르트 좌표계와 유사한 형태(Cartesian-like-form)를 가진다. 식 (35) 유도와 비슷하게 식 (2)도 아래처럼 변환될 수 있다.
(37)
식 (37)의 치환 공식은 아래와 같다.
(38)
식 (18) 증명을 이용하여 식 (3)의 좌표 변환 특성을 보자.
(39)
동일한 방법으로 식 (4)를 변형하면 아래와 같다.
(40)
위에서 유도한 변환 공식을 행렬로 표현하면 아래와 같다.
(41)
(42)
여기서 $(\cdot)^T$는 전치 행렬(transpose)이다. 식 (41)과 (42)에 있는 벡터는 아래와 같이 모두 공변 벡터이다.
(43)
식 (41)과 (42)의 관계식은 참고문헌 [3], [6], [7]에 나오는 변환식과 동일하다. 유도하는 방법은 제각각이지만 최종 결과는 동일하므로 아무 방법이든지 쉬운 방식을 택하면 된다.
.jpg)
(a) 투명 망토가 없는 경우
.jpg)
(b) 투명 망토가 있는 경우
[그림 2] 투명 망토가 작동하는 모습(출처: wikipedia.org)
식 (41)과 (42)에서는 어떤 좌표계이더라도 맥스웰 방정식이 데카르트 좌표계와 유사한 형태(Cartesian-like-form)를 가짐이 중요하다. 데카르트 좌표계 $X$에서 출발하면 임의의 좌표계 $U$에서 데카르트 좌표계와 유사한 형태를 가짐을 보였기 때문에 임의의 좌표계 $U$에서 또다른 임의의 좌표계 $V$로 가는 좌표 변환을 정의하고 식 (33)에서 (40)에 이르는 과정을 되풀이하면 모든 임의의 좌표계가 데카르트 좌표계와 유사한 형태를 가짐을 증명할 수 있다. 또한, 데카르트 좌표계만 풀 수 있다면 좌표 변환 (41)과 (42)에 의해 임의의 좌표계 문제도 풀 수 있게 된다[5]. 이런 특성은 수치 해석 소프트웨어를 설계할 때 매우 유용한 개념이 된다. 왜냐하면, 데카르트 좌표계에 대한 수치 해석 코드는 작성이 쉽기 때문이다. 한 걸음 더 나아가 좌표 변환을 잘 정의하면 특정 영역에는 전자파가 접근할 수 없게 할 수도 있다[2]. 즉, 이 개념을 이용하면 [그림 2]와 같은 투명 망토가 되기 위한 좌표 변환 기반의 유전율과 투자율을 정의할 수 있다.
[1] U. Leonhardt , "Optical conformal mapping," Science, vol. 312, no. 5781, pp. 1777–1780, June 2006.
[2] J. B. Pendry, D. Schurig, and D. R. Smith, "Controlling electromagnetic fields," Science, vol. 312, no. 5781, pp. 1780–1782, June 2006.
[3] D.-H. Kwon and D. H. Werner, "Transformation electromagnetics: An overview of the theory and applications," IEEE Antennas Propagat. Magazine, vol. 52, no. 1, pp. 24–46, Feb. 2010.
[4] E. J. Post, Formal Structure of Electromagnetics: General Covariance and Electromagnetics, Amsterdam: North-Holland, 1962.
[5] A. J.Ward and J. B. Pendry, "Refraction and geometry in Maxwell’s equations," J. Modern Optics, vol. 43, no. 4, pp. 773–793, 1996.
[6] G. W. Milton, M. Briane, and J . R. Willis, "On cloaking for elasticity and physical equations with a transformation invariant form," New J. Phys., vol. 8, pp. 248/1–20, Oct. 2006.
[7] S. G. Johnson, "Coordinate transformation & invariance in electromagnetism," Notes for the Course 18.369 at MIT, 2007 and 2010.
[다음 읽을거리]
1. 투명 망토의 원리
2. 원통형 투명 망토의 설계
(4: 반변 벡터의 공변 도함수)
(5: 공변 벡터의 공변 도함수)
(6)
(7: 쿨롱의 법칙)
(8: 패러데이의 법칙)
(9: 비오–사바르의 법칙)
(10: 변위 전류 포함 암페어의 법칙)
(11)
(16)