1. 삼각 함수
2. 미분법의 의미
3. 좌표계 기반 벡터
4. 유클리드 기하학
모든 도형 중에서 가장 완전한 도형은 [그림 1]의 원(圓, circle)이다. 중심(center)에서 거리(반지름: radius)가 같은 모든 점을 모은 원은 모난 각 없이 모든 위치에서 완벽하게 동일한 곡률을 가진다. 유클리드 기하학(幾何學, Euclidean geometry)[1]에 나오는 주요 도형도 직선(直線, straight line)과 원이다.

[그림 1] 원의 모양(출처: wikipedia.org)
원의 정의를 이용해 원의 방정식을 써보면 다음과 같다.
여기서 원의 중심은 $(a, b)$, 반지름은 $r$이다.
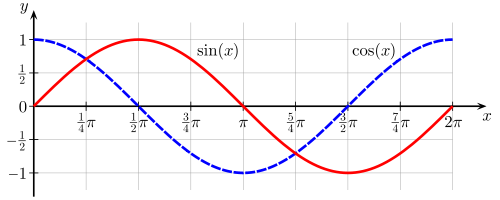
[그림 2] 사인과 코사인 함수(출처: wikipedia.org)
원의 방정식을 [그림 2]의 삼각 함수(trigonometric function)를 이용해 표현하면 다음과 같다.
 (2)
(2)
여기서 $\phi$는 원을 그리기 위한 매개변수로 0에서 $2\pi$까지 변할 수 있다.
[그림 3] 원의 둘레 길이(출처: wikipedia.org)
식 (2)를 고려해 $x$ = $r \cos \phi$, $y$ = $r \sin \phi$를 식 (3)에 대입하면 쉽게 $C$ = $2 \pi r$을 증명할 수 있다.

[그림 4] 원의 면적(출처: wikipedia.org)
원의 면적 $A$도 적분법 기반으로 다음처럼 계산할 수 있다.
 (4)
(4)
 (4)
(4)
[그림 5] 양파 껍질의 모양(출처: wikipedia.org)

[그림 6] 양파 껍질 적분법의 원리(출처: wikipedia.org)
양파 껍질 적분법(onion skin integration)을 적용하면 원의 면적은 식 (3)의 원 둘레 길이를 이용해 다음처럼 계산된다.
 (5)
(5)
여기서 생각할 문제가 하나 있다. 인류의 역사와 함께 했던 원의 둘레 길이가 왜 이렇게 쉽게 계산될까? 그건 바로 다음의 라디안(radian) 정의 때문이다.
 (6)
(6)
여기서 $l$은 호의 길이(arc length), $r$은 반지름(radius), $\theta$는 라디안으로 정의한 각도이다. 식 (19)의 우변은 라디안 $\theta$를 $360^\circ$ 기준 $\vartheta$로 바꾸는 식이다. $\theta$ = $\pi$ rad을 대입하면 $\vartheta$ = $180/\pi \cdot \pi$ = $180^\circ$를 얻을 수 있다. 또한 식 (6)을 보면 라디안에 원의 둘레 길이 의미가 들어가 있기 때문에 라디안을 이용해 식 (3)처럼 둘레 길이를 계산하기는 동어 반복일 수 있다.

[그림 7] 원주율을 고민하는 아르키메데스(출처: wikipedia.org)
그러면 라디안을 쓰지 않고 어떻게 원의 둘레 길이를 계산할까? 아르키메데스Archimedes of Syracuse(대략 기원전 287–212)가 제안한 다음 다각형 근사법을 써보자.
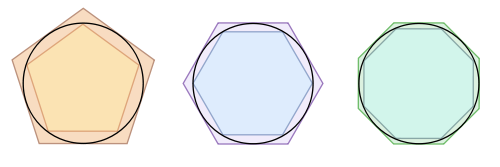
[그림 8] 아르키메데스의 다각형 근사법(출처: wikipedia.org)
원에 내접과 외접하는 정$n$각형인 경우 원의 둘레 길이 $C$는 다음 부등식을 만족한다.
 (7)
(7)
여기서 $\phi_{\rm tot}$는 원을 한 바퀴 돈 각도인 $360^\circ$이다. 식 (7)에서 $n$을 무한대로 보내면[혹은 $\phi_n \to 0$] 다음으로 표현할 수 있다.
 (8)
(8)
또한 $\phi \to 0$일 때 $\cos \phi \to 1$임은 분명하므로 $\sin \phi / \phi$는 어떤 유한한 값으로 수렴해야 한다.[∵ 기하학적으로 원의 둘레 길이가 하나의 값으로 정해짐은 확실하다.] 라디안은 이 값을 1로 둔 경우이다. 라디안 관점으로 $360^\circ$는 $\phi_{\rm tot}$ = $2 \pi$이다. 결과적으로 원주율(圓周率, ratio of circumference) $\pi$는 다음의 관계식을 이용해 구할 수 있다.
 (9)
(9)
여기서 사인값과 탄젠트값은 정$n$각형에 대한 삼각 함수표로 구한다. 만약 $n$= $4$인 경우는 원주율을 간단히 어림할 수 있다.
 (10)
(10)혹은 $n$ = $10$이면 $3.0902 < \pi < 3.2492$가 되어 정사각형 경우보다 원주율을 더 정확하게 어림할 수 있다. 즉, $n$이 커질수록 더 정확한 원주율을 구할 수 있다.
식 (1)과 (2)의 원의 방정식을 이용하면 기본 도형인 원의 다양한 성질을 쉽게 증명할 수 있다.

[그림 9] 원의 접선(출처: wikimedia.org)
[원의 접선(tangent to a circle)]
원의 접선은 항상 원에 수직이다.
[증명: 원의 방정식]
미분법(differentiation)을 이용하면, 중심이 $(0, 0)$인 원 위의 점 $(x, y)$에서의 접선[그림 9의 선분 $\overline{CA}$]은 다음 기울기를 가진다.
 (11)
(11)
중심 $O$ = $(0, 0)$에서 원 위의 점 $(x, y)$로 가는 벡터(vector)를 $\bar p$ = $(x, y)$라 하면 접선 벡터 $\bar t$ = $(1, -x/y)$는 벡터 $\bar p$에 항상 수직이다.
 (12)
(12)
[동영상: 원의 접선 정리 증명]
[증명: 기하학]
귀류법(歸謬法, contradiction)을 적용하기 위해 [그림 9]의 $\angle OCA$가 수직이 아니라고 가정하자. 그러면 어떤 점 $A$에서 수직이 된다. 이 점 $A$는 원 바깥에 있으므로 $\overline{OC} < \overline{OA}$가 성립한다. 하지만 수직의 정의에 의해 $\overline{OA}$는 점 $O$에서 접선으로 가는 최소 거리여야 한다. 이는 오류이므로 $\angle OCA$는 반드시 수직이어야 한다.
______________________________[탈레스의 철학]

[그림 10] 탈레스의 정리(출처: wikipedia.org)
[탈레스의 정리(Thales' theorem)]
지름을 이루는 두 점과 원 위의 점이 이루는 삼각형은 직각 삼각형이다.
[증명: 원의 방정식]
중심이 (0, 0), 반지름이 $r$인 원을 고려하자. [그림 10]에서 $\overline{AB}^2 + \overline{BC}^2$이라 하면 다음이 성립한다.
 (13)
(13)
여기서 $A$ = $(-r, 0)$, $B$ = $(x, y)$, $C$ = $(r, 0)$이다. 식 (13)은 피타고라스의 정리(Pythagorean Theorem)을 의미하므로 $\triangle ABC$는 직각 삼각형이다.
[증명: 기하학]
증명을 위해 아래 그림을 고려하자.
[그림 11] 탈레스 정리의 증명(출처: wikipedia.org)
원의 특성으로 인해 변의 길이가 같아 $\triangle OAB$, $\triangle OBC$는 이등변 삼각형이다. 삼각형 $\triangle ABC$를 보면 $2 (\alpha + \beta)$ = $180^\circ$이므로 $\alpha + \beta$ = $90^\circ$이 된다.
______________________________
[그림 12] 바다에서 바라본 수평선(출처: wikipedia.org)
원의 방정식은 우리 머리 속에만 있을까? 아니다. 원과 직선을 포함한 기하학은 우리 주변을 설명하는데 매우 좋은 논리적인 도구이다. 예를 들면 지구가 둥글다는 사실 증명에 원 특성을 사용할 수 있다. 쉽게 말하면 복잡한 과학 관측을 하지 않더라도 단순 기하학적 논증을 통해 지구가 둥글다는 사실을 찾을 수 있다. 둥근 지구는 고대 그리스에서도 잘 알려진 사실이었다. 둥근 지구 증명을 위해 [그림 13]과 같은 수평선 관측 사고 실험을 해보자.

[그림 13] 원 상의 수평선 관측
먼저 수평선 관측을 위해 지표면에 높이 $h$가 되는 탑을 세우자. 우리가 관측하는 수평선은 $(0, y_h)$를 지나 원에 접하는 접선의 접점 $(x_0, y_0)$이다. 탑 높이 $h$에 대한 수평선의 변화를 추적하면 지구 반지름 특성을 대략적으로 예측할 수 있다. 식 (11)을 이용해 다음 결과를 유도하자.
 (14)
(14)
식 (14)에 의해 탑을 높이 쌓을수록 $x_0$가 커지기 때문에 수평선은 더 멀리까지 관측된다. 이는 우리 경험에도 부합하는 상식적인 결과이다. 만약 지구가 평평하다면 이런 결과가 생기지 않는다.[밤하늘의 별을 보면 아주 멀리서 오는 빛도 육안으로 잘 관찰된다.] 따라서 지구가 둥근 구라는 기하학적 가설을 이용해, 높은 곳에서 수평선을 관측할 때 수평선이 더 멀리 보이는 경험적 사실을 잘 설명할 수 있다. 즉 현상의 세심한 관찰과 수학적 논리를 써서 그 속에 숨어있는 과학적 사실을 명쾌히 규명할 수 있다.

[그림 14] 원으로 표현한 점과 직선 사이의 거리
점 $(x_0, y_0)$에서 직선 $ax+by+c$ = $0$ 사이의 거리 $d$는 다음과 같다.
 (32)
(32)여기서 점과 직선 사이의 거리는 최단 거리 혹은 수직인 거리로 정한다.
[증명]
[그림 14]에 의해 거리 $d$는 원의 반지름 $r$과 동일하다. 직선 $ax+by+c$ = $0$은 원의 접선이므로 식 (11)에 따라 다음과 같이 쓸 수 있다.
 (33)
(33)법선 벡터 $\bar n$을 만들기 위해 직선도 $a(x-x_1) + b(y-y_1)$ = $0$처럼 바꾼다. 여기서 $c$ = $-(ax_1 + by_1)$, $\bar n$ = $(a, b)$이다. 그러면 벡터 $\bar v$ = $(x_1, y_1) - (x_0, y_0)$는 $\bar n$에 평행하므로, $\bar v$ = $-k \bar n$이라 쓸 수 있다. 두 벡터 $\bar n, \bar v$의 크기를 고려하면, 스칼라 $k$의 크기는 $|k|$ = $r/\sqrt{a^2 + b^2}$이 된다. 따라서 원의 반지름은 다음 관계를 만족한다.
 (34)
(34)______________________________
원과 반지름 개념을 도입하면 유명한 점과 직선 사이의 거리 문제를 더욱 쉽게 해결할 수 있다.
[원의 유리형 매개변수] [2]
 (35)
(35)여기서 $x^2 + y^2$ = $1$, $t$ = $\sec \phi - \tan \phi$, $-1 \le t \le 1$이다.
[증명]
 (36)
(36)
식 (35)에 $t$ = $\sec \phi - \tan \phi$를 대입해서 정리한다.
 (36)
(36)각도 $\phi$ = $\pi/2$에서는 $t$가 존재하지 않지만, 이 각도 근방에서는 $t$ = $0$으로 잘 정의된다.
______________________________
식 (2)는 원을 그리는 유일한 매개변수가 아니며, 식 (35)처럼 다양하게 선택할 수 있다.
[1] Euclid, Elements, 300 BC. (Java 기반 설명)
[2] 김영훈, "공간의 분류와 대칭성 [2]: 기하학자의 꿈", HORIZON, 2018년 4월. (방문일 2024-01-18)
[다음 읽을거리]
1. 포물선의 방정식
2. 타원의 방정식
[2] 김영훈, "공간의 분류와 대칭성 [2]: 기하학자의 꿈", HORIZON, 2018년 4월. (방문일 2024-01-18)
[다음 읽을거리]
1. 포물선의 방정식
2. 타원의 방정식



 (1)
(1) (2)
(2) (3)
(3)

 (7)
(7)

 (10: 패러데이의 법칙)
(10: 패러데이의 법칙)
 (A.1)
(A.1) (A.2)
(A.2)
 (13)
(13)