다이폴 안테나(Dipole Antenna)

[경고] 아래 글을 읽지 않고 "다이폴 안테나"를 보면 바보로 느껴질 수 있습니다.
1. 가장 쉬운 안테나 이론
2. 안테나의 복사 저항
3. 헤르츠 다이폴

[확인] 본 페이지는 exp(jωt) 시간 약속을 사용하고 있습니다.

다이폴 안테나(dipole antenna)는 실제로 사용할 수 있는 안테나(antenna) 중에서 기하학적으로 가장 단순하며 가장 부피가 작은 안테나이다. 이론적으로 가장 단순하며 작은 안테나는 헤르츠 다이폴(Hertzian dipole)이지만 안테나 공진(resonance)이 거의 일어나지 않아 실제로는 사용할 수 없다.

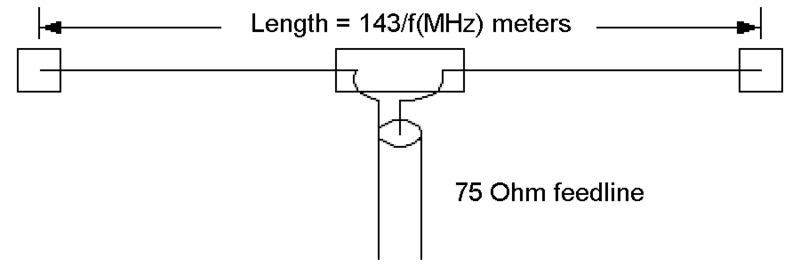
[그림 1] 반파장 다이폴 안테나의 구조(출처: wikipedia.org)

[그림 2] 반파장 다이폴 안테나의 실제 모습(출처: wikipedia.org)

다이폴 안테나는 존재하는 안테나 중에서 기하학적으로 가장 단순하지만 안테나 복사 문제가 쉽게 풀린다는 뜻은 아니다. 헤르츠Heinrich Hertz(1857–1894) 이후 많은 연구자들이 다이폴 안테나 문제를 풀었지만 아직은 정확한 답을 알지 못한다[1]–[3].

[그림 3] 헤르츠 다이폴 안테나

그래서, 식 (1)과 (2)에 있는 헤르츠 다이폴의 전자기장을 이용하여 다이폴 안테나의 전자기장을 근사적으로 계산한다.

                          (1)

                          (2)

즉, [그림 4]처럼 다이폴 안테나를 가장 작은 안테나인 헤르츠 다이폴을 이용해 표현한다.

[그림 4] 헤르츠 다이폴을 이용한 다이폴 안테나의 근사

그러면 굳이 다시 맥스웰 방정식을 풀 필요없이 식 (1)과 (2)에 제시한 안테나 식으로 다이폴 안테나의 전자기장을 모두 표현할 수 있다.

                          (3)

                          (4)

식 (4)에 있는 벡터 $\bar R$은 [그림 4]에 제시되어 있다. 각 헤르츠 다이폴이 만드는 전자기장을 표현하는 벡터 $\bar R$은 다음 공식으로 정의한다.

                          (5)

쉽게 생각하면 벡터 $\bar R$은 원점이 $(0, 0, z')$에 있는 구 좌표계(spherical coordinate system)의 위치 벡터(position vector)이다. 벡터 $\bar R$의 복잡성으로 인해 식 (3)과 (4)를 적분하기는 매우 어렵다. 더군다나 $z'$ 지점의 전류값 $I(z')$도 모르는 상태이다. 그래서 식 (3)과 (4)에 원역장 조건(far-field condition)을 다음처럼 적용한다.

                       (6)

원역장 조건은 기하학적으로 다음처럼 간단하게 생각할 수 있다.

[그림 5] 원역장 조건의 기하학적 의미

중앙의 검정색 화살표 길이를 기준으로 보자. 그러면 주황색 화살표 길이는 검정색보다 $d \cos \theta$만큼 짧아진다. 바다색 화살표는 검정색보다 $d \cos \theta$만큼 길어진다. 이를 수식적으로 표현하면 식 (6)이 된다. 우리 경우에는 식 (7)처럼 간단하게 원역장 조건을 기술할 수 있다.

                       (7)

                       (8)

그러면 원역장에서 $\Theta$ = $\theta$, $\Phi$ = $\phi$가 성립하여 벡터 $\bar R$의 단위 벡터는 벡터 $\bar r$의 단위 벡터와 동일하다. 그러면 식 (3), (4)는 원역장에서 다음처럼 간단하게 표현된다.

                       (9a)

                       (9b)

여기서 $I_m$은 안테나에 흐르는 최대 전류이다. 식 (9)에서 재미있는 함수는 안테나 복사 패턴(antenna radiation pattern) $P(\theta)$이다.

                       (10)

식 (10)은 전류 분포(current distribution)의 푸리에 변환(Fourier transform)이 복사 패턴이 됨을 뜻한다. 예를 들어, 전류 분포가 공간상에 광범위하게 분포되어 있으면, 복사 패턴은 매우 날카로워진다. 혹은 전류 분포가 헤르츠 다이폴처럼 매우 작은 경우는 복사 패턴이 각도에 대해 거의 일정해진다. 식 (10)을 정확히 계산하려면 다이폴 안테나의 전류 분포 $I(z')$를 알아야 한다. 하지만 정확한 전류 분포는 알 수가 없어 다이폴 안테나의 경계 조건(boundary condition)을 이용한다.  즉, $z'$ = $l/2$에서 전류가 0임은 확실하다. 그래서 전류 분포를 다음처럼 가정한다.

                       (11)

식 (11)로부터 $z'$ = $0$[안테나 입력부]에서 전류가 최대가 되기 위해서는 [그림 4]의 다이폴 길이 $l$이 반파장(half wavelength)이 되어야 한다. 그래서 보통 다이폴 안테나라고 하면 반파장 길이를 의미한다. 식 (11)을 식 (10)에 대입하여 다이폴 안테나의 복사 패턴 $P(\theta)$을 구해보자.

                       (12a)

                       (12b)

여기서 $\operatorname{Sa}(x)$는 표본화 함수(sampling function)이다. 식 (12a)에서 $\theta$ = $0, \pi$일 때는 특이점(singular point)이 될 것 같지만, 로피탈의 규칙(L'Hôpital's rule)을 이용해 계산해 보면 $\theta$ = $0, \pi$의 복사 패턴은 유한하게 잘 정해진다. 다른 관점으로 식 (12b)를 봐도 표본화 함수의 성질에 의해 $\theta$에 대한 특이점은 전혀 없다.

                       (13)

식 (13)은 매우 중요한 의미를 가진다. 즉, 다이폴 안테나는 주파수나 안테나 길이에 관계없이 어떤 경우에도 안테나가 놓인 방향으로 전자파를 복사하지 않는다. 반파장 다이폴 안테나(half-wave dipole antenna)는 복사 패턴이 다음처럼 굉장히 간단해진다.

                       (14)

다이폴 안테나의 복사 패턴 최대값을 찾기 위해 식 (12)를 $\theta$에 대해 미분한다.

                       (15)

식 (15)를 $0$으로 만드는 각도 중의 하나는 $\theta$ = $\pi/2$이다. 이 각도에서 $P(\theta)$는 최대값 혹은 최소값을 가질 수 있다.

                       (16)

각도 $\theta$ = $\pi/2$의 근방에 대해 식 (12)를 변화시켜보면, $l \le 3 \lambda /2$에 대해 $P(\theta)$의 최대값은 항상 $\theta$ = $\pi/2$이다. 안테나 길이 $l$이 $3 \lambda /2$보다 커지면 $\theta$ = $\pi/2$의 복사 패턴은 작아지기 시작한다. 왜냐하면 $\cos(kl/2) \ge 0$에 의해 $P(\pi/2)$는 $4$보다 작아져서 $\theta$ = $\pi/2$와는 다른 각도에서 최대값이 생기기 때문이다. 극단적으로 $l$ = $2 \lambda$인 경우는 $P(\pi/2)$ = $0$이 되어서 $\theta$ = $\pi/2$ 방향으로는 전자파 복사가 생기지 않는다. 다만 $l$ = $2 \lambda$가 되면, 식 (11)에 의해 $z'$ = $0$의 전류는 $0$이 되어서 급전을 할 수 없다. 즉, $l$ = $2 \lambda$인 다이폴 안테나는 급전에 문제가 있어서 현실에서 쓰기는 어렵다.

다이폴 안테나의 복사 패턴이 복잡하기 때문에, 방향도(方向度, directivity) 혹은 안테나 이득(antenna gain)을 정확히 유도하기는 어렵다. 다이폴을 구성하는 금속 도선에 손실이 없어서 복사 효율이 100%라면, 방향도 $D(\theta, \phi)$와 안테나 이득 $G(\theta, \phi)$는 서로 같아져서 방향도만 구해도 충분하다. 방향도 계산은 다이폴 안테나의 복사 세기(radiant intensity) $U(\theta, \phi)$로부터 시작한다. 이를 위해 식 (9)를 $U(\theta, \phi)$의 정의에 넣어서 정리한다.

                       (17)

방향도에 쓰이는 전체 복사 전력(total radiated power, TRP) $P_r$은 다음과 같다.

                       (18)

식 (17)과 (18)을 합쳐서 다소 복잡한 다이폴 안테나의 방향도 $D(\theta, \phi)$를 얻는다.

                       (19)

피적분 함수가 삼각 함수의 합성 함수라서 더 이상 적분을 진행하기 어렵다. 그래서 특별한 조건으로 반파장 다이폴 안테나를 선택한다. 이 때문에 $P(\theta)$는 식 (14)처럼 바뀌어서 반파장 다이폴 안테나의 방향도를 단순화할 수 있다.

                   (20)

                   (21)

여기서 $\operatorname{Cin}(x)$는 코사인 적분(cosine integral)이다. 반파장 다이폴 안테나의 복사 패턴은 $\theta$ = $90^\circ$에서 최대가 되고 크기는 $P(\theta)$ = $2$가 된다. 이 결과를 식 (21)에 대입해서 최대 방향도 $D_\text{dp}$를 결정한다.

                   (22)

데시벨(decibel)로 바꾼 $D_\text{dp}$는 대략 2.15 dBi이다. 방향도 $D_\text{dp}$는 반파장 다이폴 안테나를 기준으로 정의하는 dBd[디비디로 읽음]에도 쓰인다. 예를 들어, 반파장 다이폴 안테나의 방향도는 2.15 dBi이면서 0 dBd도 된다.

[참고문헌]

[1] C. Butler, "Evaluation of potential integral at singularity of exact kernel in thin-wire calculations," IEEE Trans. Antennas Propagat., vol. 23, no. 2, pp. 293–295, March 1975.

[2] L. Pearson, "A separation of the logarithmic singularity in the exact kernel of the cylindrical antenna integral equation," IEEE Trans. Antennas Propagat., vol. 23, no. 2, pp. 256–258, March 1975.

[3] D. H. Werner, J. A. Huffman, and P. L. Werner, "Techniques for evaluating the uniform current vector potential at the isolated singularity of the cylindrical wire kernel," IEEE Trans. Antennas Propagat., vol. 42, no. 11, pp. 1549–1553, Nov 1994.

[다음 읽을거리]
1. 다이폴 안테나의 복사 저항

평면파를 이용한 푸리에 변환 기법(Fourier Transform Technique Using Plane Waves)

[경고] 아래 글을 읽지 않고 "푸리에 변환 기법"을 보면 바보로 느껴질 수 있습니다. 
1. 맥스웰 방정식
2. 전자기장 파동 방정식
3. 페이저를 이용한 맥스웰 방정식
4. 균일 평면파의 의미
5. 푸리에 변환

6. 급속 하강 방법

[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.

전자기장 파동 방정식(electromagnetic wave equation)을 이용하면 전기장(electric field)에 대한 미분 방정식(differential equation)을 다음과 같이 얻을 수 있다.

                         (1)

식 (1)에서 시간 미분을 페이저(phasor)로 바꾸면 전기장에 대한 페이저 기반 파동 방정식을 만들 수 있다.

                          (2)

                         (3)

여기서 파수(wavenumber)와 라플라시안(Laplacian)은 다음처럼 정의한다.

                          (4)

                         (5)

식 (3)에서 $x, y$축으로는 변화가 없고[$\partial \bar E/ \partial x$ = $\partial \bar E/ \partial y$ = $0$] 오직 $z$축으로만 변한다고 생각하자. 그러면 식 (3)의 파동 방정식을 1차원으로 단순하게 생각할 수 있다.

                         (6)

그러면 식 (6)의 미분 방정식(differential equation) 해는 다음과 같은 균일 평면파(uniform plane wave)로 표현할 수 있다.

                         (7)

다음으로 2차원을 고려하기 위해 $\partial \bar E/ \partial z$ = $0$이라 가정해본다. 그러면 식 (3)은 다음처럼 표현할 수 있다.

                         (8)

식 (8)의 미분 방정식을 풀기 위해 전기장을 식 (7)처럼 평면파라고 간주해 다음처럼 풀 수 있다.

                         (9)

                         (10)

여기서 $k_z$ = $0$이다. 하지만 실제 문제에서 식 (9), (10)과 같은 접근법은 문제가 있다. 왜냐하면 $k_x, k_y$가 정해지지 않아 임의의 값이 될 수 있기 때문이다. 이런 골치 아픈 문제를 어떻게 해결할 수 있을까? 바로 다음과 같은 푸리에 변환(Fourier transform)을 쓰면 해결된다[1].

                       (11)

푸리에 변환으로 보면 어떤 함수든지 이 함수의 쌍에 대한 무한 적분으로 표현할 수 있다. 그래서, 식 (11)처럼 임의의 2차원 전기장을 다음처럼 표현할 수 있다.

                       (12)

식 (12)를 식 (8)에 넣으면 다음과 같은 미분 방정식을 얻을 수 있다.

                       (13)

여기서 $\hat E_0$는 전기장의 방향을 나타내는 단위 벡터(unit vector)이다. 식 (13)의 둘째식은 식 (6)과 동일하므로 식 (7) 유도와 비슷하게 식 (13)의 셋째식을 유도하였다. 식 (13)의 최종결과는 답이 두 개이다. 이 중에서 어떤 답을 선택해야 하나? 이를 해결하려면 복사 조건(radiation condition)을 생각해야 한다. 전자파를 관찰하면 전자파는 항상 원천을 뚫고 나오는 방향으로 복사된다. 예를 들면 백열등을 켰을 때 전자파가 백열등에 들어가는 현상을 본 적이 있는가? 아무도 없다. 백열등 속으로 들어가는 전자파는 매우 이상하다.[∵ 만약 백열등 속으로 빛이 들어가면, 이 현상은 바로 블랙홀(black hole)이다.] 따라서, 복사 조건을 이용하면 식 (13)의 셋째식 부호는 다음처럼 결정되어야 한다.

                       (14)

그러면 임의의 2차원 전기장은 푸리에 변환을 이용해 항상 다음처럼 표현되어야 한다.

                    (15)

여기서 $\xi$는 $x$방향 파수(wavenumber)이다. 파수 $\xi$는 $x$방향으로 임의의 파수를 가질 수 있음을 의미한다. 식 (15) 유도와 동일한 방법을 사용하면 임의의 3차원 전기장은 다음처럼 공식화할 수 있다.

                       (16)

여기서 $\xi, \eta$는 $x, y$방향 파수(wavenumber)이다. 식 (16)은 전기장이 특정한 방향[$\hat E_0$]으로 향해 있을 때만 맞는 식이다. 일반적인 전기장은 식 (16)을 확장해야 한다. 즉 전기장은 일반적으로 $x,y,z$방향을 가질 수 있으므로 임의의 전기장 표현식은 다음과 같아야 한다.

                       (17)

여기서 2차원 평면을 생성하는 기저 벡터(basis vector) $\hat t, \hat u$를 도입해서 $\widetilde{\bf E}(\xi, \eta)$ = $\widetilde{E_t}(\xi, \eta) \hat t + \widetilde{E_u}(\xi, \eta) \hat u$로 정의해도 된다. 식 (15)-(17)처럼 푸리에 변환을 이용하여 전기장이나 자기장을 표현하는 방식을 푸리에 변환 기법(Fourier transform technique)이라 한다. 푸리에 변환만 알면 식 (15)–(17)을 쉽게 유도할 수 있어서 별것 아니라고 생각할 수 있지만, 푸리에 변환 기법 자체는 다소 난이도가 있다. 푸리에 변환은 세밀하게 접근하면 사실 단순하지 않기 때문에, 관련 내용이 책으로도 한 권 나와있다[1].

전기장의 푸리에 변환에 해당하는 $\widetilde{E}$는 식 (16)에 푸리에 변환을 취해 다음처럼 구할 수 있다.

                       (18)

식 (17)을 통해 전기장 푸리에 변환의 의미를 알 수 있다. 바로 전기장이 변하는 빈도수가 푸리에 변환이 된다. 이 빈도수를 알면 근사없이 전기장을 정확히 표현할 수 있다. 식 (17)과 아래 맥스웰 방정식(Maxwell's equations)을 이용하면 자기장도 전기장의 푸리에 변환으로 표현할 수 있다.

                       (19: 패러데이의 법칙)

                       (20)

자기장 자체를 푸리에 변환으로 표현하면 다음 관계를 얻는다.

                       (21)

유도된 결과에 따라 자기장의 푸리에 변환 $\widetilde{\bf H}$는 파수 벡터 $\bar k$와 $\widetilde{\bf E}$의 외적으로 바로 구해진다.

                       (22)

여기서 $\hat{\bf E}, \hat{\bf H}$는 $\widetilde{\bf E}, \widetilde{\bf H}$의 복소 단위 벡터(complex unit vector)이며[$|\hat {\bf E}|$ = $|\hat {\bf H}|$ = $1$], $\hat{\bf H}$ = $\widetilde{\bf E} / |\widetilde{\bf E}|$ 및 $\hat{\bf H}$ = $\widetilde{\bf H} / |\widetilde{\bf H}|$로 정의한다. 다시 아래 맥스웰 방정식(Maxwell's equations)에 식 (17)을 대입해서 다음 관계도 얻는다.

                       (23: 쿨롱의 법칙)

                       (24)

또한 다음 맥스웰 방정식의 특성으로 인해 식 (19)에 회전 연산자(curl operator)를 적용한 결과는 다시 식 (16)에 기술한 전기장 표현식으로 돌아가야 한다.

                  (25: 변위 전류 포함 암페어의 법칙)

                    (26)

전기장의 원역장 특성을 알기 위해 식 (17)에 급속 하강 방법(method of steepest descent) 방법을 적용해보자. 급속 하강 방법은 식 (27)에 소개되어 있다.

                    (27)

식 (27)을 이용하면 $z \ge 0$인 경우 전기장의 원역장은 다음처럼 표현된다.

                    (28)

따라서 식 (28)에 의해 전기장의 푸리에 변환에 해당하는 $\widetilde{\bf E}$는 전기장의 원역장에 정비례한다[2]. 또한 식 (24)를 고려하면 전기장의 푸리에 변환 $\widetilde{\bf E}$는 전자파의 전달 방향[$\bar k_0$]에 반드시 수직함을 알 수 있다. 이 특성은 균일 평면파(uniform plane wave)의 주요 성질이다.

조건 $\sqrt{\xi^2 + \eta^2} \le k$는 소멸파(evanescent wave)가 아닌 진행파(traveling wave or propagating wave)를 나타낸다. 왜냐하면 독립 변수 $\xi, \eta$의 종속 변수인 $\zeta$가 실수라서 $e^{i \zeta |z|}$는 전파하는 파동을 나타내기 때문이다. 반대로 $\sqrt{\xi^2 + \eta^2} > k$인 경우에 $\zeta$는 순허수이므로, $e^{i \zeta |z|}$가 급속히 작아져서 소멸파를 형성하며 원천에서 멀어진 영역에서는 파동이 매우 약해진다. 그래서 근사적으로 빠르게 식 (17)을 계산하려면, 전영역이 아닌 진행파만 존재하는 조건인 $\sqrt{\xi^2 + \eta^2} \le k$에서만 $\xi, \zeta$를 계산한다.

                    (29)

그 다음에 고속 푸리에 변환(fast Fourier transform, FFT)을 식 (29)에 적용해서 모든 곳의 파동을 거의 정확하게 환산할 수 있다.

[참고문헌]

[1] H. J. Eom, Wave Scattering Theory: A Series Approach Based on the Fourier Transformation, Berlin: Springer, 2001.

[2] D. T. Paris, W. M. Leach Jr., and E. Joy, "Basic theory of probe-compensated near-field measurements," IEEE Trans. Antennas Propag., vol. 26, no. 3, pp. 373–379, May 1978.

[다음 읽을거리]
1. 데카르트 좌표계의 전자장 표현식
2. 원통 좌표계의 전자장 표현식