1. 전압
2. 헬름홀츠의 정리
3. 포스터의 리액턴스 정리
[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.
(1: 쿨롱의 법칙)
(2: 패러데이의 법칙)
(3: 비오-사바르의 법칙)
(4: 변위전류 포함 암페어의 법칙)
(5)
(6)
(7)
(8)
(9)
[참고문헌]
[다음 읽을거리]
1. 전자기장의 경계 조건
2. 전압해와 전류해의 유일성
[확인] 본 페이지는 exp(-iωt) 시간 약속을 사용하고 있습니다.
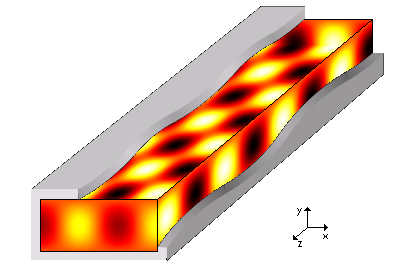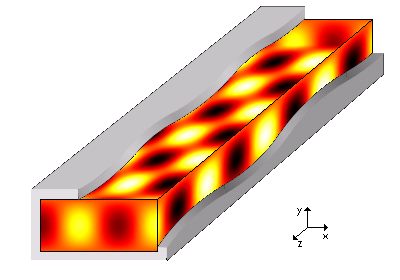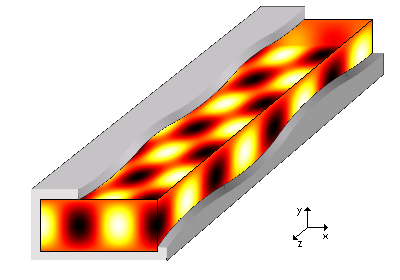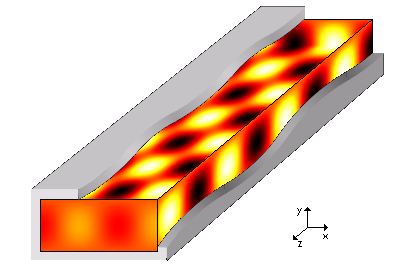
[그림 1] 도파관을 통해 전자파가 전달되는 모습(출처: wikipedia.org)
전자기 이론을 공부하다 보면 고리타분한 옛날 이론을 많이 만날 수 있다. 이런 이론 중의 하나가 전자기파에 대한 유일성 정리(唯一性 定理, uniqueness theorem)이다[1]. 별다른 추가 설명 없이 유일성 정리를 이해하려 노력하면 전자기 이론은 본인 적성과는 맞지 않다고 생각할 수도 있다. 그러면 유일성 정리를 어떻게 바라봐야 할까? 결론부터 말하면 유일성 정리가 있기 때문에 우리가 전자기파 현상을 자유롭게 이용하고 안전하게 기술 개발을 할 수 있다. 유일성 정리가 없다면 우리가 개발한 무선 장비가 정상적으로 돌아간다는 보장이 없다. [그림 1]로 예를 들면, 도파관(waveguide)을 통해 전달되는 전자파를 결정하려면 각 경계면의 조건[도파관의 표면에서 접선 전기장이 0, 도파관의 전면과 후면에서 파동은 $z$방향으로 전달]을 정확히 설정하고 계산해야 한다. 이 경계 조건(boundary condition)이 잘 정의되면, 어느 누가 문제를 풀더라도 동일한 답을 유일하게 얻을 수 있다. 이 관계를 이해하려면 유일성 정리의 말뜻부터 알아야 한다. 유일성은 말 그대로 맥스웰 방정식(Maxwell's equations)의 답은 하나임을 의미한다.
전자기파 파동 방정식(electromagnetic wave equation)의 해답은 파동 함수(wave function)임을 프랑스의 수학자 달랑베르Jean le Rond d'Alembert(1717–1783)와 스위스 수학자 오일러Leonhard Euler(1707–1783)가 증명했다. 최초 증명자인 달랑베르에 의해 맥스웰 방정식의 해가 존재함을 알았지만 그 해가 하나인지 여러 개인지는 유일성 정리를 통해 알게 된다. 그런데 해가 유일함이 왜 중요할까? 해가 여러 개가 된다고 가정한다. 그러면 입력을 포함한 조건이 같은 경우에도 전자기파의 전파 특성은 하나로 규정되지 않고 여러 개 중의 하나가 된다. 즉, 입력이 동일한데도 그 전자기파 출력은 달라질 수가 있게 된다. 이렇게 되면 맥스웰 방정식 기반으로 무선 장비 개발을 할 수가 없게 된다. 왜냐하면 실험실에서 그 특성이 검증되더라도 실제적용에서는 또 다른 특성을 가질 수 있기 때문이다. 하지만, 다행이다. 유일성 정리가 있기 때문에 조건이 같은 경우 맥스웰 방정식의 답은 단 하나이다. 이 유일성 정리로 인해 우리는 맥스웰 방정식을 이용해서 전자기파의 파동 특성을 정확하게 예측할 수 있다. 유일성 정리를 증명하기 위해 먼저 맥스웰 방정식을 살펴본다.
(1: 쿨롱의 법칙) (2: 패러데이의 법칙) (3: 비오-사바르의 법칙) (4: 변위전류 포함 암페어의 법칙)
식 (1)에서 (4)까지의 해가 두 종류라고 생각한다. 첫째쌍은 $\bar E_1, \bar H_1$, 둘째쌍은 $\bar E_2, \bar H_2$라고 생각한다. 이 두 종류의 해를 서로 빼서 차이 전자장(difference electromagnetic field) $\bar E_d, \bar H_d$를 정의한다.
(5)
식 (5)를 이용하면 식 (1)에서 (4)는 다음 식으로 변환된다.
(6)
식 (6)이 얻어지는 이유는 전하 밀도 $\rho$와 전류 밀도 $\bar J$는 입력이어서 첫째쌍 $\bar E_1, \bar H_1$, 둘째쌍 $\bar E_2, \bar H_2$에 대해 동일하다고 가정하기 때문이다. 따라서 차이 전자장 $\bar E_d, \bar H_d$는 원천이 없는 맥스웰 방정식인 식 (6)을 만족한다. 다음으로 식 (6)에 대해 포인팅의 정리(Poynting's theorem)를 적용한다.
(7)
여기서 유전율 $\epsilon$과 투자율 $\mu$를 실수부와 허수부로 분해한다. 일반적으로 유전율과 투자율은 실수로 가정하지만 실제로 모든 물질은 손실 성분을 가지고 있다. 그래서 매우 작은 값이지만 유전율과 투자율이 허수부를 가지고 있다고 가정함은 타당하다. 식 (7)이 0이 되는 이유는 표면 적분한 영역의 경계 조건(境界條件, boundary conditions)이 첫째쌍 $\bar E_1, \bar H_1$, 둘째쌍 $\bar E_2, \bar H_2$에 대해 동일하기 때문이다. 정확하게는 면적 벡터[표면적을 뚫고 나가는 법선 방향] $d\bar a$에 수직인 접선 방향 성분이 $\bar E_1$ = $\bar E_2$ 혹은 $\bar H_1$ = $\bar H_2$를 만족하기 때문이다. 따라서 표면 적분이 0이기 때문에 체적 적분도 0이 되어야 한다. 식 (7)은 실수부와 허수부로 완전히 분해가 되기 때문에 각 항목이 전부 0이 되어야 한다. 식 (7)의 실수부 두 항[$\bar E_d, \bar H_d$]은 서로 같은 부호이므로 이 값이 0이 되기 위해서는 $|\bar H_d|$ = $0$, $|\bar E_d|$ = $0$이 되어야 한다. 즉, $\bar E_1$ = $\bar E_2$, $\bar H_1$ = $\bar H_2$가 모든 체적에서 성립해야 한다. 유일성 정리에서 얻은 중요한 결과는 경계 조건이다. 경계 조건이 정해지지 않으면 전자기장은 유일하게 결정되지 않는다. 그러므로 전자기장 문제를 풀 때는 반드시 경계 조건을 고정해야 한다. 이러한 이유로 학부 교과서에도 유일성 정리를 가르치게 된다. 이는 다음에 나올 경계 조건의 중요성을 알려주기 위해서이다.
현실과 다르게 매질에 손실 없다는 이상적인 가정은 식 (7)의 유일성 증명에 오류를 만든다. 이때는 새로운 조건인 전자장의 주파수 변화 혹은 분산 관계(dispersion relation: 파동이 진행하며 퍼지는 특성) $\partial \bar E_d / \partial \omega$, $\partial \bar H_d / \partial \omega$를 고려해야 한다[1]. 차이 전자장 $\bar E_d, \bar H_d$를 적용한 포스터의 리액턴스 정리(Foster's reaction theorem)로부터 전자파의 유일성 유도를 시작한다.
(8)여기서 $d \bar a$는 체적 $v$의 내부에서 외부를 향한다. 로렌츠 진동자 모형(Lorentz oscillator model)의 관찰로부터, 무손실 매질의 주파수 미분은 다음 부등식을 항상 만족한다.
(9)따라서 식 (8)의 체적 적분은 항상 ($+$)이므로, 경계면에서 $\bar E_d$ = $\bar H_d$ = $\bar 0$, $\bar E_d$ = $\partial \bar E_d / \partial \omega$ = $\bar 0$, $\bar H_d$ = $\partial \bar H_d / \partial \omega$ = $\bar 0$, $\partial \bar E_d / \partial \omega$ = $\partial \bar H_d / \partial \omega$ = $\bar 0$ 중의 조건 하나만 만족해도 무손실 매질에서 전자장이 유일하게 결정된다. 예를 들어, [그림 1]의 도파관 내부 매질에 손실이 없더라도 도파관의 전면과 후면에 존재하는 도파관 모드(waveguide mode)의 분산 관계를 확정하면, 도파관에서 일어나는 다양한 산란 특성은 딱 하나로 계산된다.
하지만 문제 영역에 손실 없는 공진(resonance)이 생기는 경우는 우리 고민이 깊어진다. 예시적으로 [그림 1]의 도파관 끝을 막고 내부에서 원천의 입력 주파수를 바꾸면 특정한 주파수인 공진 주파수(resonant frequency) $f_r$에서 전기장과 자기장이 무한대로 발산하는 공진이 생긴다. 이로 인해 경계면에서 $\bar E_d, \bar H_d$는 0이 되지 않을 수 있다. 왜냐하면 공진 주파수인 $f$ = $f_r$에서 전자기장은 무한대로 발산하기 때문에 두 장이 같지 않을 수 있다.[무한대는 발산하는 상태라서 두 무한대의 차이는 0이 아닐 수 있다.] 그러므로 공진 구조를 계산할 때에는 전자기장의 무한대 발산을 피하는 공진 주파수의 주변 특성[$f \ne f_r$]을 선택한다. 이로 인해 공진 구조의 경계 조건은 우리 상식과 다르게 $\partial \bar E_d / \partial \omega$, $\partial \bar H_d / \partial \omega$가 적절하다[1].
[참고문헌]
[1] Q. Chu and C. Liang , "The uniqueness theorem of electromagnetic fields in lossless regions," IEEE Trans. Antennas Propagat., vol. 41, no. 2, pp. 245–246, Feb. 1993.
[다음 읽을거리]
1. 전자기장의 경계 조건
2. 전압해와 전류해의 유일성
