1. 미분법의 의미
2. 뉴턴의 운동 법칙
용수철 혹은 스프링(spring)의 움직임을 물리적으로 기술할 때 사용하는 개념이 탄성에 대한 훅의 법칙(Hooke's law of elasticity)이다. 영국의 물리학자인 훅Robert Hooke(1635–1703)가 1678년훅 43세, 조선 숙종 시절에 발표한 인장력(引張力, tensile force) 혹은 탄성력(彈性力, elastic force)에 대한 법칙이 최초이다.

[그림 1] 용수철의 운동(출처: wikipedia.org)
실제 용수철이 늘어나는 현상은 매우 복잡하지만[∵ 외부 힘에 대해 용수철 내부의 수많은 원자와 전자가 인장력을 만들기 때문에] 문제를 단순화하기 위해 선형 근사(linear approximation)를 사용한다.
 (1)
(1)
여기서 벡터 $\bar x$는 변위(displacement), $k$는 용수철 상수 혹은 스프링 상수(spring constant)이다. 용수철 상수 $k$는 1차원에 정의된 강성(剛性, stiffness) 혹은 강성 계수(stiffness coefficient)이기도 하다. 점 $x$ = $0$인 상태는 용수철의 복원력이 작용하지 않는 정상 상태이다. 훅의 법칙을 보면 외부 힘에 의해 용수철이 당겨지게 되면[$x$방향] 이 힘과 반대 방향[$-x$방향]으로 반드시 복원력이 작용한다.
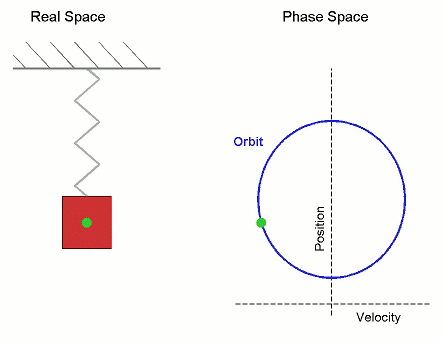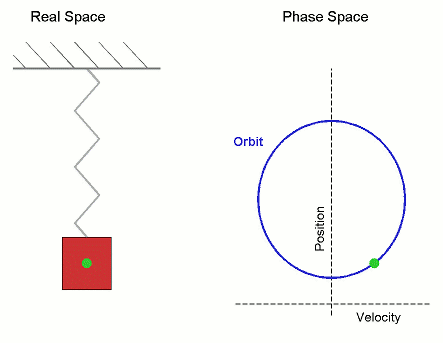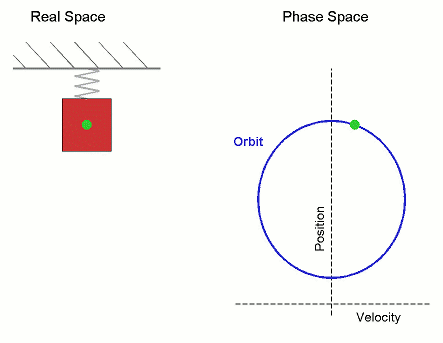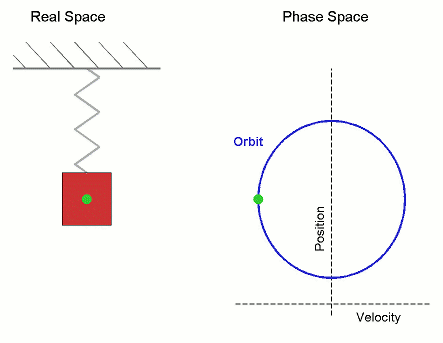
[그림 2] 외부 힘에 의한 용수철의 움직임(출처: wikipedia.org)
뉴턴의 운동 법칙(Newton's law of motion)을 이용하여 용수철의 움직임을 예측한다. 외부에서 가해지는 힘(force)을 $\bar F_{\rm in}$이라 하면 아래 미분 방정식(differential equation)이 성립한다.
 (2)
(2)
여기서 $m$은 용수철에 매달린 물체의 질량(mass)이다. 식 (2)를 이해하기 위해 2가지 경우에 대해 식 (2)의 해를 구한다.
[외부 힘이 없는 경우: $\bar F_{\rm in}$ = $0$]
 (3)
(3)[증명]
 (4)
(4)여기서 $C_1$, $C_2$는 임의의 상수이다.
______________________________
상수 $C_1$, $C_2$는 초기 조건(initial condition)을 이용해서 결정해야 한다. 결정해야 하는 상수가 2개이므로 초기 조건은 2개가 필요하다.
[외부 힘이 주파수를 가진 경우]
 (5)
(5)[증명]
식 (5)는 일종의 미분 방정식이므로 일반해와 특수해(particular solution)를 합하여 해를 구할 수 있다. 일반해는 식 (4)와 같으므로 식 (5)의 특수해를 계산한다.
 (6)
(6)______________________________
식 (4)에 등장하는 $f_0$는 용수철의 공진 주파수(resonant frequency)라고 한다. 식 (6)에서 외부 힘의 주파수를 공진 주파수로 주면 용수철이 움직이는 진폭은 무한대가 된다. 즉, 외부 힘에 의해 용수철은 무한대의 에너지를 얻게 된다. 실제로는 손실이 있어 이렇게 되지 않고 손실에 의해 최대 진폭이 결정되게 된다. 최악의 경우는 가해준 공진 주파수에 의해 용수철이 끊어질 수도 있다.
용수철이 저장하는 위치 에너지(potential energy)는 아래처럼 계산한다.
 (7)
(7)
여기서 $x$ = $0$이 위치 에너지의 기준점[$E$ = $0$]이다. 탄성 한계(elastic limit)를 넘어가는 특성까지 탄성력으로 표현하려면 식 (7)부터 출발해 일반화시킨다. 테일러 급수(Taylor series)는 모든 연속 함수를 멱급수(power series) 형태로 표현할 수 있으므로 식 (7)을 일반적으로 쓰면 다음과 같다.
 (8)
(8)
여기서 선형 근사가 성립하는 탄성 범위(elastic range) 내에서는 $dE/dx|_{x = 0}$은 0이다. 식 (8)을 구배(gradient) 형태로 미분하면 식 (9)와 같은 탄성력을 얻을 수 있다.
 (9)
(9)
식 (9)에 제시한 일반화된 훅의 법칙을 유도하기 위해 위치 에너지를 급수 전개했다. 탄성력을 기준으로 급수 전개하지 않았던 이유는 무엇인가? 탄성력과 같은 힘은 현재 순간 순간의 특성을 동적으로 표현하지만, 에너지는 모든 동적이 상태가 종료된 정적인 특성을 표현한다. 그래서 급수 전개의 기준으로 에너지가 힘보다 더 유리하다. 탄성력을 표현할 때 위치 에너지의 미분[$dE/dx|_{x = 0}$]이 0이라고 생각했다. 이 가정은 항상 맞을까? 아니다. 위치 에너지의 미분이 0이 아니라면 중력 같은 일정한 힘이 있다는 뜻이다. 우리는 탄성력에만 관심을 집중했기 때문에 중력과 같은 일정 힘을 무시했을 뿐이다. 이와 같은 논의를 바탕으로 식 (8)을 보면 에너지의 일차 미분은 중력과 같은 일정 힘이며, 에너지의 이차 미분은 용수철 상수($k$)이다.
1. 줄에 대한 파동 방정식
질문이 있습니다. 음...정확하게 어떻게 질문해야하지..
답글삭제힘에 관해서인데 보통 저희가 힘이라고 하면 F=ma를 떠올리잖아요?
그런데 요즘 파인만의 물리학 강의라는 책을 보고 있는데
선형미분방정식으로 F=ma+cv+kx와 같은 식들이 나오더군요.
여기서 ma와 cv, kx는 전혀 별개의 힘으로 봐야하나요?
아니면 ma에서 kx나 cv가 유도가능한 것인지?
cv는 운동량에서 유도한다고 쳐도 그게 동일한 것인지도 의문이고...
일단 각각 뉴턴제2법칙, 저항력, 용수철의 복원력 정도로 보고 있습니다만
이게 정확하게 이해는 잘 가지않네요.
책을 계속 보긴 할테지만 좀 도움되는 조언을 얻을 수 있으면 좋을 것 같습니다.
탄성력과 견인력은 실험에 기반한 경험 법칙입니다. 물질 내부를 구성하는 분자 특성을 고려해 유도할 수 있을지도 모르지만, 그 관점보다는 눈에 보이는 분명한 현상을 근사적으로
삭제기술한 것이 탄성력과 견인력 공식입니다.
뉴턴의 운동 법칙은 경험 기반이기는 하지만, 이 법칙은 에너지/힘/운동량의 관계를 기술하는 더 근본적인 정의입니다.
(3)식을 시간에 대하여 미분하면 md^2v/dt^2=-kv 가 나온다고 하는데 잘이해가 안가요. 설명좀 부탁드립니다.
답글삭제식 (3)은 식 (2)에서 외부 힘을 0으로 둔 거예요. 식 (2)는 뉴턴의 제2 법칙입니다.
삭제답변감사합니다. 아직 문제가 풀리지 않아서요 제가 이메일로 첨부로 보내려고 하는데 검토해주실수 있으시겠어요?
삭제알겠습니다. 다시 말씀드리자면,
삭제ma=-kx 일때 이것을 시간에 대하여 미분 한다고 하네요
그러면 결과적으로 md^2v/dt^2=-kv 가 된다고 책에 설명되어 있는데요. 전 이과정이 이해가 가질 않아서요. 부탁드립니다. 전파거북이 선생님
일단 선생님은 아닙니다, Unknown님. ^^
삭제질량이 고정이면 가속도는 속도의 미분($= \bar a = d \bar v / dt$)이고, 속도는 변위의 미분($= \bar v = d \bar x / dt$)이에요. 뉴턴의 제2 법칙을 다시 한 번 보세요.
안녕하세요~^^ 공부하다가 모르는것이 있으면 항상 여기부터 찾아오게 되네요 ㅎㅎ 수준별 설명 정말 감사드립니다..!
답글삭제질문이 있는데요.. 혹시 이 내용은 어느 정도 수준인가요? 제가 물리 2를 배우고 있고 현재 단진자에 대해 배우고 있는데 이 내용을 알면 도움이 될까요..??
아.! 그리고 ce^jwt가 뭔지도 궁굼합니다..
삭제반갑습니다, 익명님. ^^
삭제1. 여기 내용은 대학 수준입니다. 물리2를 공부하실 때는 도움이 안될 가능성이 커요. 물리 개념 이해에 더 집중하는 게 좋을 듯합니다.
2. 미분 방정식을 풀 때는 보통 해(답)를 가정합니다. 그래서 답이 될 것 같은 함수로 $e^{j \omega t}$를 쓴 거예요. $C$는 초기 조건을 맞출 상수고요.
질량이 계산값과 실제값이 다른이유는뭔가여??
답글삭제무슨 뜻인가요, Unknown님? 잘 모르겠어요.
삭제우리가 아는 훅의 법칙은 선형근사된 F=-kx 이고, 실제 훅의 법칙은 항의 개수가 무한이 많은 식이라고 선생님이 말씀해주셨는데....'실제 훅의 법칙'이 뭔지 설명 부탁드립니다!
답글삭제후크의 법칙은 탄성 범위(elastic range)에서만 선형이고, 탄성 범위를 벗어나면 비선형으로 변합니다. 이걸 함수로 표현하려면 테일러 급수 같은 형태로 쓸 수 있을 것 같은데요. 아마도 선생님께서 이 부분을 강조해주신 것 같네요.
삭제그럼 탄성 범위에서는 탄성력과 늘어난길이가 완벽한 비례관계인가요?
답글삭제실험 법칙이기 때문에 완벽하지는 않지만, 선형 근사가 잘 성립해요.
삭제